Schätzung von VaR und ConVaR für den Aktienkurs des kasachischen Unternehmens

In den letzten Jahrzehnten ist die Weltwirtschaft regelmäßig in diesen Wirbel von Finanzkrisen geraten, von denen jedes Land betroffen ist. Es führte fast zum Zusammenbruch des bestehenden Finanzsystems. Aufgrund dieser Tatsache verwenden Experten für mathematische und wirtschaftliche Modellierung Methoden zur Kontrolle der Verluste des Vermögenswerts und des Portfolios in der Finanzwelt (Lechner, LA, und Ovaert, TC) (2010). Es gibt einen zunehmenden Trend zur mathematischen Modellierung eines Wirtschaftsprozesses zur Vorhersage des Marktverhaltens und zur Bewertung seiner Nachhaltigkeit (ebenda). Ohne die notwendige Aufmerksamkeit auf die Kontrolle und Bewertung von Bedrohungen zu richten, versteht jeder, dass er auslösen kann enorme Kosten in der Entwicklung der Organisation oder sogar bankrott gehen.

Value at Risk (VaR) war schließlich ein regelmäßiger Ansatz, um das Risiko zwischen Instituten des Finanzsektors und seiner Aufsichtsbehörde zu erfassen (Engle, R. und Manganelli S., 2004). Das Modell wird ursprünglich angewendet, um den Verlustwert im Anlageportfolio innerhalb eines bestimmten Zeitraums sowie bei einer bestimmten Eintrittswahrscheinlichkeit zu schätzen. Neben der Tatsache, dass der VaR im Finanzsektor eingesetzt wird, gibt es viele Beispiele für die Bewertung des Risikowerts in verschiedenen Bereichen, z. B. die Erwartung, dass das medizinische Personal das Ressourcenmanagement im Gesundheitswesen entwickelt. Zinouri, N. (2016). Trotz seiner angewandten Primitivität in einem realen Experiment besteht das Modell aus Nachteilen bei der Bewertung (ebenda).

Ziel des Berichts ist eine Beschreibung des vorhandenen VaR-Modells einschließlich einer seiner Upgrade-Versionen, nämlich Conditional Value at Risk (CVaR). Im nächsten Abschnitt und Abschnitt 3 werden der Bewertungsalgorithmus und das Testen des Modells erläutert. Zur anschaulichen Veranschaulichung wird der erwartete Verlust für den Vermögenswert eines kasachischen Unternehmens geschätzt, das über einen langen Zeitraum an der Finanzbörse gehandelt wird. In den letzten Abschnitten 4 und 5 werden die Ergebnisse der Forschungsarbeit diskutiert und demonstriert.

Hintergrund

Es wird angenommen, dass die erste Verwendung des VaR durch die riesigen Finanzorganisationen vor bis zu 40 Jahren und in der Folge der VaR bei anderen Handelsunternehmen populär geworden ist, selbst die Finanzaufsichtsbehörden haben sich mit dem Modell befasst (Linsmeier, TJ, und Pearson, ND) 2000). Beispielsweise hat die US-amerikanische Börsenaufsichtsbehörde (Securities and Exchange Commission) den VaR 1997 in eine Liste quantitativer Methoden zur Berechnung des Marktrisikos und des Eigentums eingetragen (ebenda).

Tatsächlich ist der VaR nach Artikeln von Lechner, LA, und Ovaert, TC (2010) sowie Linsmeier, TJ und Pearson, ND (2000) eine Schätzgleichung, ausgedrückt in Währungseinheiten, die den Verlust im Größenbereich nicht überschreiten während eines bestimmten Zeitraums und eines bestimmten Konfidenzniveaus. Typischerweise beträgt das Konfidenzniveau der Modellschätzung (99%, 97,5%, 95%) oder mit anderen Worten die Wahrscheinlichkeit, dass ein ungünstiger Fall eingetreten ist, und der Einfluss auf den Markt 1, 2,5 und 5 Prozent (ebenda).

Die bekannte Gleichung des VaR kann beschrieben werden (Phelps S, 2018):

$$$(1) \ VaR (X) = \ min \ \ {x \ \ epsilon \ R: 1-F_x (-x) \ geq \ alpha \}$

Wobei X eine Zufallsvariable ist, die den Betrag des Portfoliowerts ausführt, und eine kumulative Verteilungsfunktion ist (ebenda).

Auf der anderen Seite bezeichnet Hooper GP (1996, zitiert in Lechner, LA, und Ovaert, TC 2010) den VaR mit Vertrauen, das Alpha auf ganz elementare Weise definiert:

$$$(2) \ VaR ^ \ alpha (X) = \ sigma \ sqrt {\ delta t} N ^ {- 1} \ alpha$

Wo $$$\ sigma$ist die Standardabweichung ausgewählter Aktienrenditen, $$$\ delta t$ist die Quadratwurzel des festen Zeitraums und $$$N ^ {- 1}$ist die kumulative Verteilungsfunktion (CDF) für eine Normalverteilung (Lechner, LA, und Ovaert, TC 2010).

Obwohl der VaR eine bekannte und gehandhabte Methode zur Schätzung des entschiedenen Portfoliorisikos ist, gibt es in einem Fall Mängel bei der Messung der Anfälligkeit für endgültige Marktprobleme, nämlich, dass das Beispiel mit der Wahrscheinlichkeit zusammenhängt, dass extreme Marktereignisse nicht angemessen erfasst werden der Normalverteilung (Capiński, MJ 2015). Um dieses Problem zu lösen, wurde der Conditional Value at Risk (CVaR) erstellt, der den erwarteten Verlustwert anstelle des VaR berücksichtigt (ebenda). CVaR definiert als:

$$$(3) \ CVaR ^ \ alpha (X) = \ frac {1} {\ alpha} \ int ^ \ alpha_0 VaR ^ \ beta (X) d \ beta = \ frac {-1} {\ alpha} q ^ \ beta (X) d \ beta$

$$$(4) \ CVaR ^ \ alpha (X) = - \ frac {1} {\ alpha} (E [X 1 _ {\ {X \ leq q ^ \ alpha (x) \}}] + q ^ \ alpha (X) (\ alpha-P [X \ leq q ^ \ alpha (X)]))$

Wo Ahn D.-H. et al. (1999, zitiert in Capiński, MJ 2015) interpretieren $$$-q ^ \ alpha (X)$
als VaR von X Zufallsvariable (Rendite eines Aktienkurses) mit Wahrscheinlichkeit $$$\ alpha$und definiert als das obere Quantil von X.

Darüber hinaus bestätigen Acerbi C. und Tasche D. (2002, zitiert in Capiński, MJ 2015): „Der CVaR ist eine kohärente Risikomaßnahme“. Rockafellar, RT und Uryasev, S. (2000) stellen fest, dass CVaR zusätzliche Merkmale aufweist: übergangsäquivariante, positiv homogene, konvexe usw.

Das folgende Kapitel des Artikels zeigt die Implementierung des bekannten Value at Risk (VaR) und des Conditional Value at Risk (CVaR), die ebenfalls als Expected Shortfall (ES) angekündigt wurden und in der Arbeit von Rockafellar, RT, und Uryasev, S. (2000) festgestellt wurden. durch den Einsatz von Informationstechnologie für reale Daten.

Methodik

Betrachten wir die am häufigsten verwendeten Methoden zur Berechnung des VaR sowie seine Vor- und Nachteile.

Nach dem Bericht von Lechner, LA, und Ovaert, TC (2010) ist die historische Simulation ein weit verbreiteter Ansatz zur Bewertung des VaR und seiner Modifikation. Bei der historischen Modellierung der Daten nehmen wir die Werte der finanziellen Schwankungen für das Portfolio, die bereits aus früheren Messungen bekannt sind. Es ist daher nur logisch, dass der Nachteil dieser Methode darin besteht, dass es unmöglich ist, Vorhersagen für Portfolios ohne Informationen darüber zu erstellen. Die Monte-Carlo-Methode ist in vielerlei Hinsicht identisch mit der Methode der historischen Modellierung, die für hochpräzise Techniken verwendet wird. Der Hauptunterschied besteht darin, dass die Berechnung der Monte-Carlo-Simulation nicht auf realen Daten basiert, sondern auf zufällig generierten Werten basiert. Der Vorteil dieser Methode ist die Möglichkeit, eine große Anzahl von Situationen zu berücksichtigen und das Marktverhalten unter extremen Bedingungen nachzuahmen, und es besteht keine Notwendigkeit einer Annäherung zwischen Risikofaktoren und Änderungen in einem Portfolio (Glasserman, P., Heidelberger, P. und Shahabuddin, P., 2002). Der offensichtliche Nachteil ist der große Rechenaufwand, der zur Implementierung dieses Ansatzes erforderlich ist (ebenda).

Dies sind natürlich nicht die einzigen Methoden zur Berechnung von VaR-Modellen. Darüber hinaus gibt es sowohl einfache lineare als auch quadratische Modelle der Preisvorhersage sowie eine ziemlich komplizierte Variationsmethode, die im Aufsatz nicht behandelt wurden.

Datenanalyse

Als sekundäre Daten zum Testen der genauen Bewertung wird der Bestand an KAZ Minerals entnommen. Zur Verdeutlichung der Arbeit wird der bereinigte Schlusspreis für die Simulation in einem Modell herangezogen. Die Aktien der KAZ Minerals Company (KAZ.L) gehören zu den erfolgreich gehandelten Wertpapieren zwischen kasachischen Unternehmen an der London Stock Exchange (LSE) und sind in der Liste der Premium Equity Commercial Companies (London Stock Exchange, 2019) aufgeführt. Das Unternehmen präsentiert sich als massives Kupferbergbauunternehmen in Kasachstan (Kazminerals.com. 2019).

Die historischen Daten des Aktienkurses werden von der Yahoo Finance-Website (Finance.yahoo.com, 2019) heruntergeladen. Um die Gültigkeit der Arbeiten sicherzustellen, wird der Zeitraum von einem Jahr vom 22. März 2018 bis zum 22. März 2019 eingehalten. Um die Informationsstörung zu vermeiden, werden bei der Analyse die historischen Daten des KAZ.L-Aktienkurses im CSV-Format (Comma-Separated Values) heruntergeladen, da das CSV-Format mit dem Microsoft Excel-Programm (Excel) kompatibel ist. . Die ausgewählten Daten des Projekts werden mithilfe von Excel in Abbildung 1 als Liniendiagramm dargestellt.

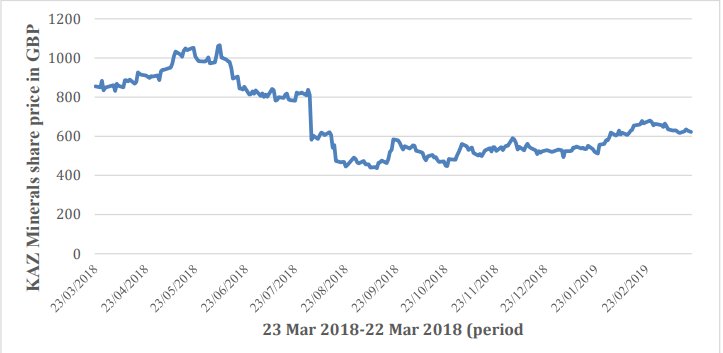
Abbildung 1. Die Dynamik der Veränderung Der Aktienkurs von KAZ Minerals für ein Jahr

Aufgrund der Einschränkung der Berichtszeitleiste werden die Daten anstelle einer Programmiersprache wie Python zur Implementierung von Bewertungsmodellen vollständig in Excel analysiert.

Ergebnisse

Im vorherigen Abschnitt wurden die Modelle zur Prognose der potenziellen Verluste in einem Portfolio basierend auf der VaR- und CVaR-Gleichung und den verwendeten Änderungen des Aktienkurses von KAZ Minerals vom 23. März 2018 bis 23. März 2019 von der offiziellen Webquelle Yahoo Finance (Finance.yahoo) heruntergeladen. com, 2019). Beide Gleichungen werden für jedes Datum aus dem gewählten Zeitraum ausgeführt.

Tabelle 1 zeigt die durchschnittliche tägliche Geschäftsrendite, eine Standardabweichung der Renditen, einen Mindestwert der Renditen und einen Maximalwert der Renditen für dieses Beispiel.

Tabelle 1. Mittlere Rendite und Standardabweichung der Renditen

Der entsprechende Mittelwert beträgt -0.0006 und die Standardabweichung 0,0355 der Renditen für das ausgewählte eindeutige Wertpapier KAZ Minerals. Darüber hinaus beträgt die Varianz der Renditen 0,0013. Darüber hinaus sollte unterstrichen werden, dass in den Forschungsarbeiten von Vee, DNC und Gonpot, P. N (2014) die kasachischen Aktienrenditen einen signifikanten Wert in Bezug auf die Volatilität aufwiesen, die Schätzung jedoch mit dem Index der kasachischen Börse vor und in Bezug stand Nach dem Zeitraum 2008. Außerdem sollte erwähnt werden, dass der Maximalwert unter den Renditen 0,0998 und der Minimalwert unter den Renditen -0,2829 in der Verlustverteilung beträgt. In Tabelle 2 sind die Maximal- und Minimalwerte des bereinigten Schlusskurses (KAZ.L) beim Handel mit Pfund Sterling (GBP) an der Londoner Börse vom 23. März 2018 bis 22. März 2019 aufgeführt.

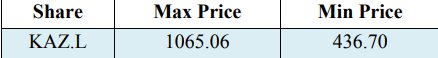
Tabelle 2. Der maximale und minimale Aktienkurs von KAZ Minerals in GBP

Der folgende Schritt ist die Bewertung des Value at Risk (VaR) und des Conditional Value at Risk (CVaR) für das Konfidenzniveau - 0,99, 0,972 und 0,95. Die Werte sind in Tabelle 3 angegeben.

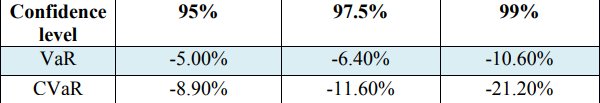
Tabelle 3. VaR- und CVaR-Werte der Renditen

Die Stichprobengröße der Simulation beträgt 252 Einheiten vom 23. März 2018 bis 22. März 2019 während eines Jahres.

Diskussion

In dem Bericht zeigen VaR- und CVaR-Gleichungen den glaubwürdigen Wert bei den Schätzmodellen für einen Aktienkurs eines kasachischen Unternehmens in der kurzfristigen Periode. Mit diesen Werten auf der einen Seite liefern beide Methoden angemessene Ergebnisse, um den Wert der Bedrohungen für das Anlageportfolio zu bewerten (Linsmeier, TJ, und Pearson, ND 2000; Lechner, LA, und Ovaert, TC 2010).

Darüber hinaus ist nach den Ergebnissen aus Tabelle 2 die nächste Mitteilung unkompliziert, dass die Werte für CVaR im Vergleich zu den VaR-Werten bei allen Konfidenzniveaus massiver sind. Dies lässt sich dadurch erklären, dass der CVaR das gewählte durchschnittliche Portfoliorisiko eingeht und daher am Ende der Verlustverteilung empfindlicher ist als der VaR. Dies beweist erneut, dass CVaR ein kohärentes Risiko darstellt (Acerbi C. und Tasche D., 2002, zitiert in Capiński, MJ 2015; Rockafellar, RT und Uryasev, S. 2000). Zum Beispiel veranschaulichen im Hinblick auf die Angemessenheit beider Schätzmodelle mit einem Konfidenzniveau von 99% VaR und CVaR den signifikanten Prozentsatz des Verlusts aus Aktienrenditen. Um genau zu sein, könnte festgestellt werden, dass der VaR -10,60% und der CVaR -21,20% beträgt. Es ist ziemlich klar, warum die kolossalen Maßnahmen von CVaR mit einem gegebenen Konfidenzniveau von 99% aufgrund der Tatsache, dass die Bandbreite des Aktienkurses während des Zeitraums bei einem Höchstkurs von 1065,06 GBP und einem Mindestkurs von 436,70 GBP liegt.

Fazit

Nach alledem sollte noch einmal erwähnt werden, dass das Ziel des Berichts darin besteht, die Schätzung des Wertes eines möglichen Verlusts für das kasachische Unternehmen (KAZ Minerals) über einen Zeitraum vom 23. März 2018 bis 22. März 2019 aufzuzeigen. gebildet auf den Gleichungen Value at Risk (VaR) und Conditional Value at Risk (CVaR). Die Leistungen der Simulation werden im gleichen Zeitraum miteinander verglichen. Die Ergebnisse zeigen den signifikanten Wert für jede Methode und belegen die früheren Arbeiten auf demselben Gebiet, dass CVaR im Vergleich zum VaR genauere Messwerte aufweist (Acerbi C. und Tasche D., 2002, zitiert in Capiński, MJ 2015; Rockafellar, RT, und Uryasev, S.2000).

Trotz Kritik ist der VaR bis heute ein weit verbreitetes Instrument in allen Finanzinstituten, und es gibt eine breite Palette seiner Modifikationsversion. Aufgrund der Hindernisse der komplexen Berechnung in der Tiefenforschung wird das Experiment unter Verwendung von Microsoft Excel anstelle einer Programmiersprache wie Python durchgeführt, und die Ergebnisse werden im Bericht enthüllt. Die Ergebnisse des Aufsatzes können als Grundlage für weitere Arbeiten zur Verwendung komplexer Risikobewertungen für das Portfolio in der Börsenbranche, der Versicherungsbranche und der Investmentbranche dienen.