Zur Anwendung der Theorie der ARMA-Prozesse in der Ingenieurpraxis

Im Folgenden werden wir einige Worte über die zeitdiskrete Alternative zu mathematischen Modellen in Form von linearen Differentialgleichungen sagen, die allgemein bekannt, aber für Ingenieure eher unerwartet ist, nämlich autoregressive Modelle - gleitender Durchschnitt und sehr ungewöhnliche Aussichten für eine solche Modellierung, deren Fähigkeiten deutlich übersteigen Was Sie von LDU gewohnt sind.

Die Liste der möglichen Fähigkeiten der Technologie umfasst die Analyse von Systemen mit einer eingehenden Störung, die für die Beobachtung nicht zugänglich ist, die Bestimmung der Resonanzeigenschaften solcher Systeme, des Spektrums und des Prozesses der externen Anregung, die spektrale Schätzung von Prozessen anhand ihrer kurzen Realisierungen, die Modellierung des Verhaltens von Systemen bei einer niedrigen Abtastfrequenz über die Zeit usw.





ARMA-Verfahren, die Ökonomen (genauer gesagt „Ökonomen“) bekannt sind, sind Spezialisten für automatische Regelung viel weniger bekannt und werden meiner Meinung nach von Maschinenbauingenieuren und Funkelektronikern, insbesondere von Ingenieuren der „alten Schule“, fast nie verwendet. Der Artikel versucht, einige mögliche Anwendungsbereiche der ARMA-Theorie in der Ingenieurpraxis aufzuzeigen.
Kurz gesagt, vereinfacht für diejenigen, die mit dem Thema nicht vertraut sind, um das es sich tatsächlich handelt. Der stochastische zeitkontinuierliche Prozess x (t) aus offensichtlichen "digitalen" Gründen "in der Praxis stimmt gewöhnlich mit der zeitdiskreten Sequenz x [i] mit dem Abtastintervall Δt überein.
Grundsätzlich ist für jeden Prozess x [i] eine Darstellung der Form möglich

x [i] - a ₁ · x [i-1] - a ₂ · x [i-2] - ... - a _p · x [ip] = b ₀ · f [i] + b ₁ · f [i- 1] + ... + b _q · f [iq] (1),

wobei a _k und b _k konstante (für dieses Modell) Koeffizienten sind, die als Autoregression-Moving-Average-Modell mit der Reihenfolge der Autoregression p und des gleitenden Durchschnitts q bezeichnet werden. oder ein ARMA (p, q) -Modell, f [i] ist eine Art "eingehender" Prozess, um den es etwas niedriger geht. Oft wird (1) in einer etwas anderen Form geschrieben (6).
Grundsätzlich ist es nur ein digitaler Filter, der sowohl rekursive AR- als auch nicht rekursive MA-Teile enthält.
Es gibt eine Entsprechung zwischen den ARMA (p, q) -Modellen und linearen Systemen (zum Beispiel mechanisch), die beispielsweise durch die bekannte lineare Differentialgleichung der Form beschrieben werden


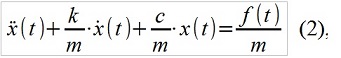
wobei m, c, k die Masse, Steifheit und Dämpfung des mechanischen Systems ist, f (t) die äußere Kraft ist. Das ARMA-Gegenstück sieht folgendermaßen aus:

x [i] - a ₁ · x [i-1] - a ₂ · x [i-2] = b ₁ · f [i-1] (3),

Die Koeffizienten des Modells können ziemlich leicht durch die Eigenwerte λ ₁ und λ ₁ * (der Kürze halber wird der "oszillierende" Fall betrachtet) des linearen Systems und Δt gefunden werden:

a ₁ = z + z *, a ₂ = - z · z *, b ₁ = j (z * -z) · Δt / (2mω ₁ ),

wobei z = exp (λ ₁ · Δt), λ ₁ = -ε ₁ + jω ₁ , j die imaginäre Einheit ist, * die komplexe Konjugation ist

als Referenz:

Für das Testsystem ist m = 1 kg, c = 100 N / m, k = 0,75 kg / s, Δt = 0,12 s.
erhaltenes ARMA (2,1) -Modell

x [i] - 0,69433x [i-1] + 0,91393 x [i-2] = 0,010696f [i-1]

(Eine sehr kurze Erklärung, wie (3) aus (2) erhalten wird. Die Impulsübergangsfunktion unseres linearen Systems, d. H. Die Antwort des Systems auf einen einzelnen Impuls:



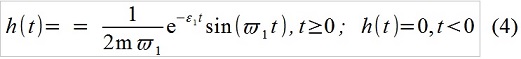
Datensatz (2) in der "integralen" Form wird als "Faltung" f (t) und h (t) bezeichnet, was bedeutet, dass die äußere Wirkung als eine Folge von Elementarimpulsen betrachtet wird. Schreiben Sie in diskreter Zeit beispielsweise Folgendes:



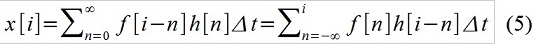
Durch Addition von x [i], x [i-1] und x [i-2] unter Verwendung der ausgewählten Faktoren 1, a ₁ und a ₂ erreichen sie die gegenseitige Vernichtung der unendlichen „Schwänze“ h [i] - auf der rechten Seite sind f [i] · H [0] = f [i] · 0 und f [i-1] · h [1] = f [i-1] · b ₁ . Aus Sicht der ARMA-Theorie wird das unendlich dimensionale Modell des gleitenden Durchschnitts MA (∞) in ARMA (2,1) transformiert (obwohl einige sagen werden, dass ein rein autoregressives Modell AR (2) = ARMA (2,0) zufällig erhalten wurde.

Bemerkung 1. Ein Leser, der mit der digitalen Verarbeitung von Prozessen vertraut ist, wird sagen, dass es nicht sehr korrekt ist, nur h (t) zu diskretisieren - es ist notwendig, die Funktion h (t) durch die Frequenz auf 1 / (2Δt) (Filter) zu begrenzen. Andernfalls liegt ein Frequenzmaskierungsfehler vor. Die Diagramme des Frequenzgangs und des Phasengangs unseres Systems, des „analytischen“ und des ARMA-Modells zeigen, warum dieser Fehler in den meisten technischen Fällen höchstwahrscheinlich vernachlässigt werden kann (Abb. 1) (hier liegt der Frequenzgang auf einer logarithmischen Skala).

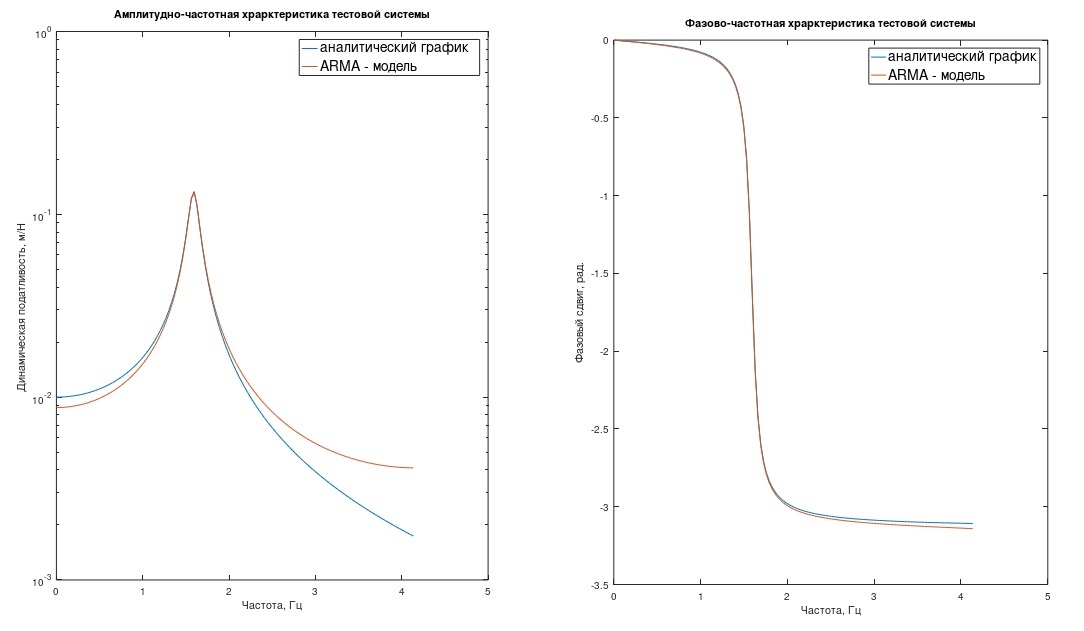
Abb. 1 Frequenzgang und Phasengang des Testsystems.

Bemerkung 2. In der Praxis kann die Ordnung des ARMA-Modells erheblich größer sein als das oben betrachtete Beispiel, beispielsweise aufgrund mehrerer Freiheitsgrade eines mechanischen Systems oder eines komplexen Spektrums realer äußerer Einflüsse.

Bemerkung 3. Sehr wichtig. Es gibt Methoden (hier nicht berücksichtigt - es können viel mehr Artikel darüber geschrieben werden), die es ermöglichen, die Parameter des ARMA-Modells (nämlich die Reihenfolge der Modelle p und q und die Koeffizienten a _k und b _k ) nur durch den resultierenden Prozess x [i] unter der Annahme zu schätzen dass f [i] ein hypothetisches weißes Rauschen ist, dessen Varianz ebenfalls geschätzt werden kann. Im Allgemeinen ist eine solche Bewertung der Hauptteil der gesamten ARMA-Theorie. Diese Methoden unterscheiden sich zwar nicht in besonderer Perfektion, sind jedoch von erheblichem Interesse.

Nun darüber, warum all dies tatsächlich in der Praxis angewendet werden kann (oder könnte). Neben der ganz offensichtlichen - schnellen Konstruktion von "manuell" gedämpften (und ungedämpften) Sinuskurven aus den ersten beiden Punkten und den beiden Koeffizienten a ₁ und a ₂ gibt es meiner Meinung nach ernsthaftere Anwendungen dieser Modelle in der Ingenieurpraxis.

1. Nun, für die Simulation des Systembetriebs - wir geben dem Eingang ein echtes externes Signal f [i], wir erhalten x [i] am Ausgang:

x [i] = a ₁ · x [i-1] + a ₂ · x [i-2] + ... + a _p · x [ip] + b ₀ · f [i] + b ₁ · f [i- 1] + ... + b _q · f [iq] (6)

Das ARMA-Modell kommt mit der Aufgabe besser zurecht als das Finite-Differenzen-Modell, dies macht sich jedoch nur bei großen Abtastintervallen Δt bemerkbar. (in Fig. 2 ist Δt = 0,12 s (links) und 0,03 s). In welchen Fällen ist es sinnvoll, sich mit ARMA anzulegen - Sie entscheiden.

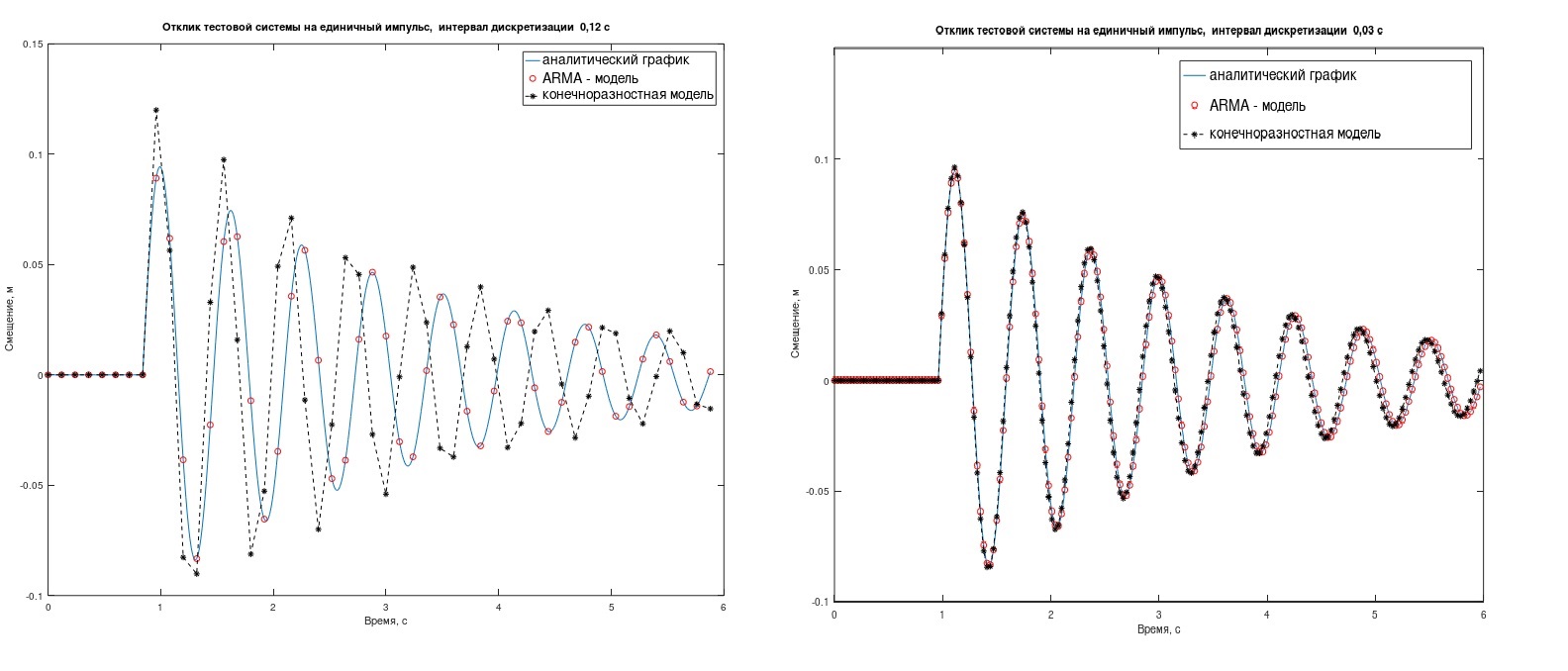
Abb. 2. Die Reaktion von Testsystemen auf einen einzelnen Impuls.

2. Zur Spektralschätzung, insbesondere wenn die Implementierungslänge des stationären Prozesses für die Beobachtung nicht ausreicht. Vielleicht ist dies die bekannteste technische Anwendung von ARMA-Modellen. Da ein bestimmter digitaler Filter und die Varianz des eintretenden weißen Rauschens für den untersuchten Prozess erhalten werden, ist die Aufgabe, eine Schätzung der PSD zu erstellen, auf offensichtliche Weise gelöst. In der Tat ist es möglich, extern sehr „glatte“ SPM-Diagramme zu erhalten und gleichzeitig den Eindruck einer hohen Auflösung zu erwecken. Die erwartete Verbesserung der Bewertung hängt damit zusammen, dass der Forscher externe Informationen über die Art des Prozesses in die Erstellung der Bewertung einbringt - normalerweise durch Festlegen einer bekannten Modellreihenfolge.
Kurz gesagt, Sie müssen wissen, wie grob diese PSD aussehen sollte. Die „explorativen“ Studien dieser Implementierung mit klassischen Methoden können wenig bewirken und beziehen sich hauptsächlich auf klassische (auf FFT basierende) Studien ähnlicher Art, jedoch mit erheblich längeren Realisierungen. Es besteht die Möglichkeit von groben Fehlern.

3. Zur Analyse der Resonanzeigenschaften des Systems und des Spektrums der äußeren Einwirkung, falls der wahre äußere Effekt nicht zur Beobachtung zur Verfügung steht. Wie bereits erwähnt, ist es möglich, bei Kenntnis des Prozesses x [i] alle Koeffizienten des Modells a _k und b _k (und die Varianz des ankommenden weißen Rauschens) zu bestimmen. Wenn Sie die Wurzeln zweier Polynome mit den entsprechenden Koeffizienten bestimmen, können Sie leicht p „Pole“ und q „Nullen“ des Modells (λ _k und μ _k ) finden und seine Übertragungsfunktion konstruieren - Sie können wahrscheinlich nicht einmal die ARMA-Form verwenden (hier) gegeben) und in der üblichen „analytischen“ Form - wie wir oben herausgefunden haben (Abb. 1), ist der Unterschied gering. Zum Beispiel haben wir für p = 5, q = 3 (während wir von den bestehenden, anscheinend Einschränkungen des Verhältnisses von p und q abstrahieren) als Option:



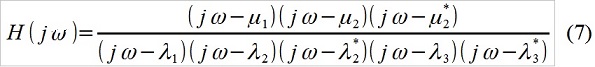
Natürlich ist alles sehr, sehr vereinfacht. Basierend auf der bekannten Natur des untersuchten Objekts (dies sind beispielsweise Polygontests der Fahrruhe des Autos) und der äußeren Einwirkung (Mikroprofil der Straße) entschied sich der Forscher, die Übertragungsfunktion beispielsweise wie folgt umzuschreiben:




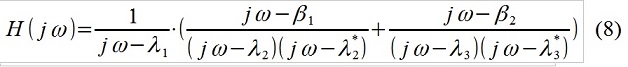
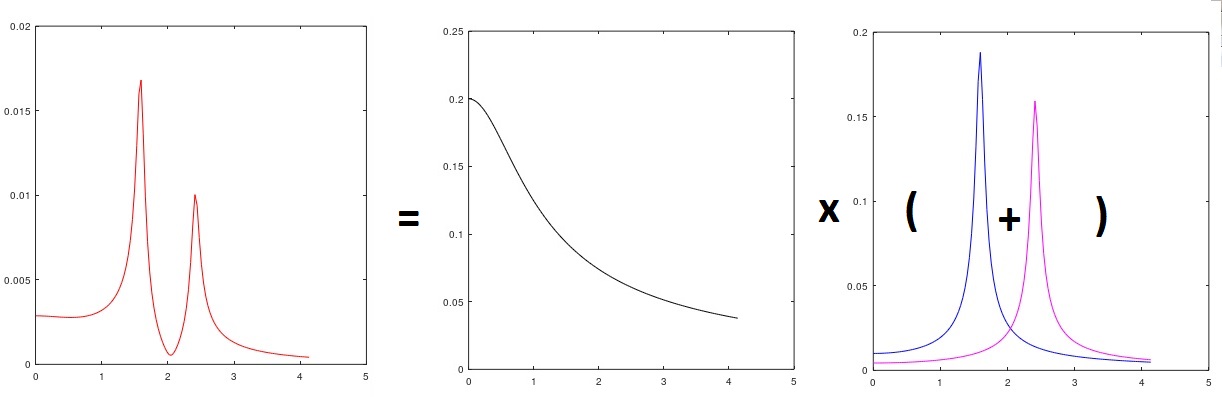
Abb. 3 Analyse des Signalspektrums mit Zuordnung der eingehenden Störung

und kommentiert - der Teil des Modells, der sich auf λ ₁ bezieht, ist offensichtlich (bis zum Quadrieren und Multiplizieren mit der Varianz des ankommenden hypothetischen weißen Rauschens) das „rosa“ Mikroprofil der Straße (Abb. 3) (dh wir haben ein unbekanntes Spektrum von Real identifiziert Das Eingangssignal - manuell ausgewählt - scheint „ähnlich“ zu sein. λ ₂ und λ ₃ sind die Resonanzeigenschaften des Körpers an der Aufhängung (möglicherweise Längswinkel- und Vertikalschwingungsmodi). Das Hauptproblem wird natürlich darin bestehen, die Parameter des ARMA-Modells zu bestimmen. Für das gerade Beschriebene können Sie manchmal ohne ARMA auf die altmodische Weise (wenn auch in elektronischer Form) gemäß dem Spektraldichtediagramm "kriechen" und die Peakbreite bei einem Pegel von -3 dB usw. messen oder eine Krümmung anwenden, manchmal sogar mit großem Erfolg .

3. Für die lineare Vorhersage x [i]. Anscheinend ist die Hauptanwendung von ARMA für Ökonomen. Aus (6) ist ersichtlich, dass, wenn die Koeffizienten des Modells unter Verwendung der oben beschriebenen Methoden geschätzt würden, der nächste Wert x [i] auf ein hypothetisches weißes Rauschen genau geschätzt werden kann, das für die Beobachtung b ₀ · f [i] unzugänglich ist, die Varianz dieses weißen Rauschens geschätzt wird zusammen mit den Koeffizienten des Modells. Normalerweise wird in diesem Fall eine dynamische (in Echtzeit) Anpassung der Modellparameter impliziert. Anscheinend kann es in Systemen zur aktiven Vibration und Geräuschreduzierung nützlich sein. TAP-Spezialisten wissen es am besten.

4. So stellen Sie einen unzugänglichen Prozess wieder her, der nicht beobachtet werden kann. Bei der Aufteilung des Modells in Teile, wie oben in Abschnitt 3 gezeigt, ist es basierend auf dem Wissen über die Art des untersuchten Prozesses möglich, das Spektrum der eingehenden Störung und die Schwingungseigenschaften des physikalischen Systems getrennt zu bewerten (das Modell in Teile aufzuteilen). Sie können noch weiter gehen - erstellen Sie einen Filter (ARMA-Modell, das Inverse des Originalmodells), der den Ausgang des Systems mit dem Eingang verbindet und mit Hilfe des resultierenden Prozesses x [i] eine temporäre Implementierung der eingehenden Störung erhält. Versuchen Sie beispielsweise, ein unverzerrtes Signal wiederherzustellen, das mit genau unbekannten linearen Verzerrungen von Geräten aufgezeichnet wurde, die für eine separate Studie nicht verfügbar sind (z. B. durch Telemetrie).

Aufgrund meines bescheidenen Wissens werde ich daher ein solches subjektives Urteil ausdrücken. Die Anwendbarkeit von ARMA-Technologien auf technische Probleme hängt stark von der Perfektion der Methoden zur Schätzung der Parameter dieser Modelle aus dem resultierenden Signal ab oder wird meiner Meinung nach durch die Unvollkommenheit dieser Methoden stark eingeschränkt. Die Anhäufung von Erfahrungen bei der Anwendung von ARMA im Ingenieurwesen scheint vor allem in Erwartung eines sehr wahrscheinlichen „Durchbruchs“ in diesem Bereich sinnvoll zu sein.