Vorwort

Ich denke, wir müssen kurz erklären, warum plötzlich so ein scheinbar triviales Thema bei der Berechnung des Energiebudgets und warum genau die CubeSat-Satelliten? Nun, hier ist alles ganz einfach: Meine kurze Unterrichtspraxis hat (für mich) gezeigt, dass dieses Thema, obwohl es grundlegend ist, beim ersten Mal nicht von allen verstanden wurde, und außerdem hatte es einige Fragen, die in der ersten Lesung nicht offensichtlich waren. Darüber hinaus scheint es, dass sie zu solchen grundlegenden Dingen immer noch Artikel in IEEE veröffentlichen, und dies wird bei weitem nicht von Studenten getan. Warum genau CubeSat? Hier ist es noch einfacher: Das Satellitenformat ist interessant (die Tatsache, dass Mikro- und Nanosatelliten vorhanden sind, versetzt viele in einen Zustand kurzen Schocks) und eignet sich daher sehr gut für Bildungszwecke.

Die Simulation wird in Python 3 aus den gleichen Gründen durchgeführt, die ich in meiner vorherigen Veröffentlichung angegeben habe . Wir werden den Fall einer niedrigen Umlaufbahn (LEO - Low Earth Orbit) betrachten und tatsächlich das Signal-Rausch-Verhältnis (SNR - Signal-Rausch-Verhältnis) am Empfängereingang über eine Abwärtsverbindung (DL - Abwärtsverbindung) berechnen. Wir werden mehrere Verzeichnisse aus Open Access verwenden und zur Verdeutlichung Diagramme erstellen.

Alle Quellcodes sind in meinem GitHub-Repository verfügbar. Ich lade alle Interessierten ein, sie zu lesen! Ich werde für die Codeüberprüfung und konstruktive Kritik sehr dankbar sein!

Lass uns gehen!

Welche Formeln werden wir berechnen?

Erstens ist dies natürlich eine bekannte Formel für das Signal-Rausch-Verhältnis auf einer logarithmischen Skala (einfach in Dezibel) für alle (am Thema Beteiligten), wobei wir alle möglichen Verluste und Verstärkungen mit einem gewissen Grad an Abstraktion berücksichtigen:

$SNR = P_t + G_t + G_r + \ eta_ {t} + \ eta_ {r} - L_r - L_t - L - L_ {add} - N [dB] \ qquad (1)$

wo - Gesamtleistung des thermischen Rauschens (hat einen bekannten Zusammenhang mit der spektralen Dichte des Rauschens $N_0 = kT_ {Rauschen}$ ) in dBm (Dezibel pro Milliwatt), P_t - Sendeleistung in dBm, G_t und G_r - Antennengewinn auf der Seite des Senders bzw. Empfängers (in dBi - isotrope Dezibel), $\ eta_ {t}$ und $\ eta_ {r}$ - Verstärkung des Sender- und Empfänger-Feeders (in dB), L_t und L_r - Verluste in Feedern (in dB), Verluste im Ausbreitungsweg der elektromagnetischen Welle in dB, $L_ {add}$ - zusätzliche Verluste (sozusagen ein gewisser Spielraum) in dB.

Im Allgemeinen ist bei den ersten sieben Begriffen mehr oder weniger klar: Dies sind Referenzdaten. Bei den letzten drei Teilnehmern des Prozesses ist es interessanter.

Thermische Rauschleistung

Wie Sie wissen, gibt es keinen Ort, an dem Sie sich vor dieser Geißel elektronischer Geräte verstecken können. Sie können nur Folgendes berücksichtigen:

$N = 10 lb \ links (\ frac {kT_ {Rauschen} B_ {Rauschen}} {10 ^ {- 3}} \ rechts) [dBm] \ qquad (2)$

wo - Boltzmann-Konstante $T_ {Rauschen} = T_a + T_e$ - äquivalente Geräuschtemperatur, T_a - die Summe der Antennenverluste und des Rauschens (Hintergrund) des Himmels, $T_e = T_0 (F_ {sys} -1)$ - Geräuschtemperatur des Empfängers ( T_0 = 290K und $F_ {sys} = 10 ^ {\ frac {NF} {10}}$ - Rauschzahl, die aus dem Rauschbild geschätzt werden kann ( - Rauschzahl) der Empfangsantenne) und $B_ {Lärm}$ - die Breite des Rauschfrequenzbandes. Sie können das Rauschband gleich der Bandbreite des Empfängers selbst nehmen gemäß [1, S. 98] jedoch die Rauschbandbreite $B_ {Lärm}$ kann etwas genauer bewertet werden als $\ gamma B.$ wo $\ gamma$ - Konstante von 1,002 bis 1,57 (bezieht sich auf die Empfängerkonfiguration).

Zusätzliche Verluste

Hier können Sie entweder eine garantierte Versorgung beziehen, die in der Regel aus denselben Verzeichnissen stammt, oder tiefer gehen und alles selbst berechnen.

In diesem Abschnitt verlasse ich mich fast ausschließlich auf das gute alte Cantor-Lehrbuch, nämlich diesen Teil davon [1, S. 88-96]. Wenn die Leser relevantere maßgebliche Quellen haben - bitte teilen Sie diese mit, ich denke, sie werden für alle nützlich sein.

Worauf wir in erster Linie achten:

Verlust durch Brechung und Ungenauigkeit der Antennenausrichtung ( Antennenstrahlverlust )

Sind als bezeichnet $L_b = 10log_ {10} (1+ (2 \ Theta / \ Theta_ {0,5}) ^ 2)$ wo $\ Theta$ - Strahlbreite und $\ theta_ {0.5}$ - die Strahlbreite der halben Leistung und hängen, egal wie schwer zu erraten, von den Eigenschaften bestimmter Antennengeräte ab:

Atmosphärische Phaseneffekte

Wenn Sie den Klassikern glauben, wirken sich diese Verluste hauptsächlich auf die Datenübertragungsrate aufgrund der Bandbreite des Empfängers aus, da es wünschenswert ist, das Band gemäß Tabelle 1 [1, S. 91]. Um Phasenverzerrungen zu vermeiden.

Tab. 1. Maximale Empfängerbandbreite für verschiedene Bereiche.

Trägerfrequenz, GHz	0,5	1	5	10
Bandbreite des Empfängers (B), MHz	10	25	270	750

Es ist jedoch anzumerken, dass die Zahlen sehr beeindruckend sind und aufgrund des thermischen Rauschens oft nicht berücksichtigt werden.

Verlust aufgrund einer Fehlanpassung der Antennenpolarisation

Kann in Abhängigkeit von Elliptizitätskoeffizienten geschätzt werden $e_1$ und $e_2$ (Ich füge einen Ausschnitt aus dem sowjetischen Buch als Abbildung 1 bei).

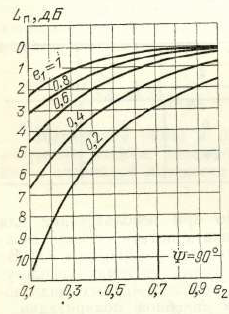
Abb. 1. Abhängigkeit von Verlusten aufgrund von Polarisationsfehlanpassungen zwischen Sende- und Empfangsantennen von der Elliptizität. [1, S. 93]

Ich bin jedoch auf diesen Parameter als Referenz gestoßen. Bei der Berechnung des Energiebudgets für den NanoCom AX100 beträgt der Polarisationsverlust beispielsweise 3 dB (der atmosphärische Verlust beträgt 2,1 dB, der ionosphärische Verlust 0,4 dB).

Atmosphärische Dämpfung

Wir können diesen interessanten Parameter entweder gemäß den Empfehlungen der ITU bewerten oder selbst berechnen. Glücklicherweise gibt es spezielle Bibliotheken wie diese .

Dämpfung entlang des Weges der Ausbreitung elektromagnetischer Wellen (Pfadverlust)

Ohne weiteres wenden wir zunächst die Friis-Formel an :

$L = 20 lg \ frac {\ lambda} {4 \ pi d} [dB] \ qquad (3)$

wo $\ lambda$ - elektromagnetische Wellenlänge (bezieht sich in bekannter Weise auf die Trägerfrequenz $f_0 = \ frac {c} {\ lambda}$ , Ist die Geschwindigkeit der elektromagnetischen Welle (die Lichtgeschwindigkeit, wenn einfacher) und - die Entfernung zwischen den Satelliten und der Bodenstation.

Und hier kommen wir vielleicht zu der interessantesten Frage: Welche Entfernung sollten wir für Berechnungen nehmen? Wie bereits in der Einleitung erwähnt, betrachten wir LEO-Satelliten, was bedeutet, dass sich unser angeblicher Satellit relativ zur Erde bewegt (im Gegensatz zum geostationären Fall, in dem der Satellit sozusagen über einem Punkt hängt).

Sie können natürlich alles so weit wie möglich vereinfachen, indem Sie das Schema als Grundlage nehmen (Abb. 2), wenn davon ausgegangen wird, dass die Umlaufbahn des Kommunikationssatelliten ungefähr „über dem Kopf“ unserer Bodenstation liegt.

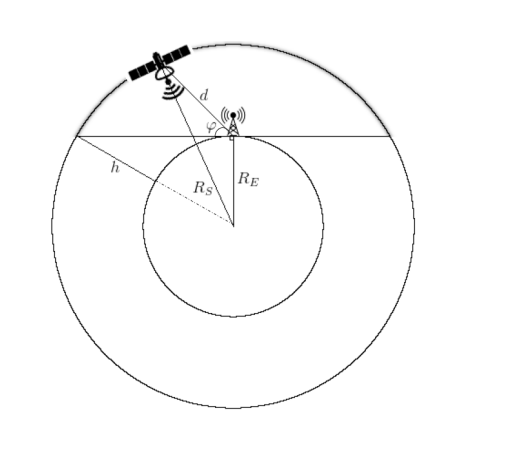
Abb. 2. Schematische Beschreibung der CubeSat-Flugbahn im erdnahen Orbit [2].

Dann kann die Entfernung nach folgender Formel berechnet werden:

$d = \ sqrt {(R_E + h) ^ 2-R_E ^ 2cos ^ 2 \ phi} - R_Esin \ phi \ qquad (4)$

wo R_E - Es gibt tatsächlich den Radius der Erde, - Höhe der Satellitenumlaufbahn und $\ phi$ - Höhenwinkel.

Sie können jedoch etwas mehr Dampf machen, sich wieder dem Klassiker (bereits anders) zuwenden [3, S.110-123] und alles berechnen, was bereits relativ zu den tatsächlichen geografischen Koordinaten der Bodenstation ist (
$lat_ {gs}$ und $long_ {gs}$ ) und die tatsächliche Position des Satelliten (augenblicklich aufsteigender Knoten - $L_ {Knoten}$ und Umlaufbahnpol - Momentaner Umlaufbahnpol ich ) Machen Sie sich bereit, es wird viel Trigonometrie geben:

$d_ {min} = R_E \ frac {\ sin \ lambda_ {min}} {\ sin \ eta_ {min}} \ qquad (5)$

wo $\ sin \ lambda_ {min} = \ sin (90 ^ 0 - i) \ sin (lat_ {gs}) + \ cos (90 ^ 0 - i) \ cos (lat_ {gs}) \ cos (long_ {gs} - (L_ {Knoten} - 90 ^ 0))$ - minimaler zentraler Winkel der Erde, $\ eta_ {min} = arctan \ frac {\ sin \ rho \ sin \ lambda_ {min}} {1 - \ sin \ rho \ cos \ lambda_ {min}}$ - minimaler Nadirwinkel, $\ rho = arcsin \ frac {R_E} {R_E + h}$ Ist der Winkelradius der Erde. Die maximale Entfernung kann berechnet werden durch:

$d_ {max} = R_E \ frac {\ sin \ lambda_ {max}} {\ sin \ eta_ {max}} \ qquad (6)$

wo $\ sin \ eta_ {max} = \ sin \ rho \ cos \ epsilon_ {min}$ und $\ lambda_ {max} = 90 ^ 0 - \ epsilon_ {min} - \ eta_ {max}$ ( $\ epsilon_ {min}$ - minimaler Satellitenhöhenwinkel).

So fassen Sie eine kurze Zusammenfassung der Parameter zusammen :

Was wir als Ausgangspunkte wählen : Trägerfrequenz, Umlaufbahnhöhe (möglicherweise die Position des Satelliten und die geografischen Koordinaten der Bodenstation - hängt von der Genauigkeit ab, die wir erhalten möchten);
Wir finden geräteabhängige und einstellbare Parameter : Sendeleistung, Empfängerbandbreite;
Wir finden Referenzdaten : Antennengewinn und -verlust, Feedergewinn und -verlust, Rauschtemperatur, zusätzlicher Verlust.

Wir simulieren, was als Ergebnis passiert ist

Als Quelle für technische Parameter für die Downlink-Bewertung stehen Beispiele aus der Praxis für Transceiver und Antennen für CubeSat-Satelliten wie NanoCom AX100 und NanoCom ANT430 zur Verfügung . Für eine größere Bandbreite ist es natürlich besser, das S-Band zu berücksichtigen. Für diesen Bereich sind die NanoCom ANT2000- Patchantenne und der NanoCom SR2000- Transceiver erhältlich.

Wir beginnen zu überprüfen, was passiert ist.

from SmallSatLB import * import pandas as pd

Alle Logik ist bedingt in zwei Optionen unterteilt: 'Entwurf' , in dem Formel (4) zur Berechnung der Entfernung verwendet wird; und "genau" , in denen die Formeln (5) und (6) verwendet werden.

"Entwurf"

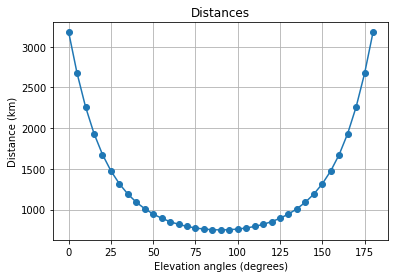
 l_d = LinkBudget(750*1e3, 'draft') #   (   ) d = l_d.distance() #   phi = np.pi*np.array(range(0,181,5))/180 #     plt.plot(180*phi/np.pi, d*1e-3, '-o') plt.title('Distances') plt.xlabel('Elevation angles (degrees)') plt.ylabel('Distance (km)') plt.grid()

 snr, EIRP = l_d.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) #  SNR plt.title('Expected SNRs') plt.xlabel('Elevation angles (degrees)') plt.ylabel('SNR (dB)') plt.legend() plt.grid()

Schönheit!

"präzise"

 l_p = LinkBudget(750*1e3, 'precise',\ L_node = 100+90, incl = 90 - 61.5,\ lat_gs = 22, long_gs = 200, eps_min = 5) snr, EIRP = l_p.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) print(min(snr)) print(max(snr))

 >>> 5.556823874020452 >>> 8.667000351847676

Im Allgemeinen hier: Wir haben ein kleines Tool für primäre "Schätzungen" und Berechnungen, um wie viel das Signal geschwächt wird, während es vom Satelliten zur Erde geht (oder umgekehrt).
Vielen Dank für Ihre Aufmerksamkeit!

Liste der verwendeten Literatur :

Kantor L. Ya., Askinazi G. B. Satellitenkommunikation und Rundfunk: ein Nachschlagewerk . - Radio und Kommunikation, 1988.
Otilia Popescuy, Jason S. Harrisz und Dimitrie C. Popescuz, Entwurf des Kommunikationssubsystems für Nanosatelliten-CubeSat-Missionen: Betriebs- und Implementierungsperspektiven, 2016, IEEE
Wertz JR, Larson WJ Analyse und Design von Weltraummissionen, Bibliothek für Weltraumtechnologie. - Microcosm Press und Kluwer Academic Publishers, El Segundo, CA, USA, 1999.

Wir berechnen das Energiebudget einer Funkleitung für einen Satelliten im CubeSat-Format