Glücklicher Kosmonautik-Tag! Wir übergaben der Druckerei ein
"kleines Buch über Schwarze Löcher". In diesen Tagen zeigten Astrophysiker der ganzen Welt, wie schwarze Löcher aussehen. Zufall? Wir denken nicht;) Also warte, bald erscheint ein erstaunliches Buch, geschrieben von Stephen Gabser und Frans Pretorius, übersetzt von dem wunderbaren Pulkovo-Astronomen alias Astroded Kirill Maslennikov, dem legendären Vladimir Surdin, der wissenschaftliche Bearbeitung vorgenommen hat, und der Trajectory Foundation unterstützte seine Veröffentlichung.
Auszug "Thermodynamik der Schwarzen Löcher" unter dem Schnitt.
Bisher haben wir Schwarze Löcher als astrophysikalische Objekte betrachtet, die sich während Supernova-Explosionen gebildet haben oder in den Zentren von Galaxien liegen. Wir beobachten sie indirekt und messen die Beschleunigungen von Sternen in ihrer Nähe. Die berühmte Registrierung von Gravitationswellen durch den LIGO-Empfänger am 14. September 2015 wurde zu einem Beispiel für direktere Beobachtungen von Kollisionen mit Schwarzen Löchern. Die mathematischen Werkzeuge, mit denen wir die Natur von Schwarzen Löchern besser verstehen, sind: Differentialgeometrie, Einstein-Gleichungen und leistungsstarke analytische und numerische Methoden zur Lösung von Einsteins Gleichungen und zur Beschreibung der Raum-Zeit-Geometrie, die Schwarze Löcher erzeugen. Und sobald wir eine vollständige quantitative Beschreibung der vom Schwarzen Loch erzeugten Raumzeit geben können, kann das Thema Schwarze Löcher aus astrophysikalischer Sicht als geschlossen betrachtet werden. In einer breiteren theoretischen Perspektive gibt es noch viele Möglichkeiten für die Forschung. Der Zweck dieses Kapitels ist es, über einige theoretische Errungenschaften der modernen Schwarzlochphysik zu sprechen, in denen die Ideen der Thermodynamik und der Quantentheorie mit der allgemeinen Relativitätstheorie kombiniert werden, was zu unerwarteten neuen Konzepten führt. Die Grundidee ist, dass Schwarze Löcher nicht nur geometrische Objekte sind. Sie haben eine Temperatur, eine enorme Entropie und können Manifestationen einer Quantenverschränkung aufweisen. Unsere Diskussion der thermodynamischen und Quantenaspekte der Schwarzlochphysik wird skizzenhafter und oberflächlicher sein als die in den vorhergehenden Kapiteln vorgestellte Analyse rein geometrischer Raum-Zeit-Merkmale in Schwarzen Löchern. Aber diese und insbesondere die Quantenaspekte sind ein wesentlicher und wesentlicher Bestandteil der laufenden theoretischen Studien über Schwarze Löcher, und wir werden uns sehr bemühen, wenn nicht komplizierte Details, dann zumindest den Geist dieser Arbeiten zu vermitteln.
In der klassischen allgemeinen Relativitätstheorie - wenn wir über die Differentialgeometrie von Lösungen von Einsteins Gleichungen sprechen - sind Schwarze Löcher wirklich schwarz in dem Sinne, dass nichts aus ihnen herauskommen kann. Stephen Hawking hat gezeigt, dass sich diese Situation vollständig ändert, wenn wir Quanteneffekte berücksichtigen: Schwarze Löcher emittieren Strahlung einer bestimmten Temperatur, die als Hawking-Temperatur bekannt ist. Für schwarze Löcher von astrophysikalischer Größe (d. H. Von schwarzen Löchern mit Sternmassen bis zu supermassiven) ist die Hawking-Temperatur im Vergleich zur Temperatur des kosmischen Mikrowellenhintergrunds - Strahlung, die das gesamte Universum füllt, vernachlässigbar, was übrigens selbst als eine Variante der Hawking-Strahlung angesehen werden kann. Die von Hawking durchgeführten Berechnungen zur Bestimmung der Temperatur von Schwarzen Löchern sind Teil eines breiteren Forschungsprogramms auf diesem Gebiet, das als Thermodynamik von Schwarzen Löchern bezeichnet wird. Ein weiterer wichtiger Teil dieses Programms ist die Untersuchung der Entropie von Schwarzen Löchern, die die Menge an Informationen charakterisiert, die in einem Schwarzen Loch verloren gehen. Gewöhnliche Objekte (wie ein Becher Wasser, ein Stück reines Magnesium oder ein Stern) haben ebenfalls Entropie, und eine der zentralen Aussagen der Thermodynamik von Schwarzen Löchern ist, dass ein Schwarzes Loch dieser Größe mehr Entropie aufweist als jede andere Form von Materie, die darin untergebracht werden kann ein Gebiet der gleichen Größe, aber ohne die Bildung eines Schwarzen Lochs.
Bevor wir uns jedoch eingehend mit den Problemen der Hawking-Strahlung und der Entropie der Schwarzen Löcher befassen, wollen wir einen kurzen Ausflug in die Bereiche Quantenmechanik, Thermodynamik und Verschränkung machen. Die Quantenmechanik wurde hauptsächlich in den 1920er Jahren entwickelt und diente hauptsächlich dazu, sehr kleine Materieteilchen wie Atome zu beschreiben. Die Entwicklung der Quantenmechanik führte zur Erosion grundlegender physikalischer Konzepte wie der exakten Position eines einzelnen Teilchens: Es stellte sich beispielsweise heraus, dass die Position eines Elektrons bei seiner Bewegung um einen Atomkern nicht genau bestimmt werden kann. Stattdessen wurden den Elektronen die sogenannten Bahnen zugeordnet, in denen ihre tatsächlichen Positionen nur im probabilistischen Sinne bestimmt werden können. Für unsere Zwecke ist es jedoch wichtig, nicht zu schnell auf diese - probabilistische - Seite der Sache überzugehen. Nehmen Sie das einfachste Beispiel: ein Wasserstoffatom. Es kann sich in einem bestimmten Quantenzustand befinden. Der einfachste Zustand eines Wasserstoffatoms, der als Grundzustand bezeichnet wird, ist der Zustand mit der niedrigsten Energie, und diese Energie ist genau bekannt. Im Allgemeinen erlaubt uns die Quantenmechanik (im Prinzip), den Zustand eines Quantensystems absolut genau zu kennen.
Wahrscheinlichkeiten treten auf, wenn wir bestimmte Fragen zu einem quantenmechanischen System stellen. Wenn zum Beispiel definitiv bekannt ist, dass sich das Wasserstoffatom im Grundzustand befindet, können wir fragen: "Wo ist das Elektron?" und nach den Gesetzen des Quanten
Mechanik bekommen wir zu dieser Frage nur eine bestimmte Schätzung der Wahrscheinlichkeit, ungefähr so etwas wie: "Das Elektron befindet sich wahrscheinlich in einer Entfernung von bis zu einem halben Angström vom Kern eines Wasserstoffatoms."
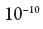
Meter). Wir haben jedoch die Möglichkeit, durch einen bestimmten physikalischen Prozess die Position des Elektrons viel genauer als auf einen Angström zu bestimmen. Dieser in der Physik weit verbreitete Prozess besteht darin, ein Photon mit einer sehr kurzen Wellenlänge in ein Elektron zu starten (oder, wie Physiker sagen, ein Photon auf ein Elektron zu streuen) - danach können wir den Ort des Elektrons im Moment der Streuung mit einer Genauigkeit rekonstruieren, die ungefähr der Wellenlänge entspricht Photon. Dieser Prozess ändert jedoch den Zustand des Elektrons, so dass es sich danach nicht mehr im Grundzustand des Wasserstoffatoms befindet und keine genau definierte Energie mehr hat. Für einige Zeit wird seine Position jedoch fast genau bestimmt (genau auf die Wellenlänge des dafür verwendeten Photons). Eine vorläufige Beurteilung der Position des Elektrons kann nur im probabilistischen Sinne mit einer Genauigkeit von etwa einem Angström durchgeführt werden, aber sobald wir es gemessen haben, wissen wir genau, was es war. Kurz gesagt, wenn wir ein quantenmechanisches System auf irgendeine Weise messen, geben wir ihm zumindest im allgemein akzeptierten Sinne „gewaltsam“ einen Zustand mit einem bestimmten Wert der Größe, die wir messen.
Die Quantenmechanik ist nicht nur auf kleine, sondern (wie wir glauben) auf alle Systeme anwendbar, aber für große Systeme werden quantenmechanische Regeln schnell sehr komplex. Das Schlüsselkonzept ist die Quantenverschränkung, ein einfaches Beispiel dafür ist das Konzept des Spins (Rotation). Einzelne Elektronen haben einen Spin, so dass in der Praxis ein einzelnes Elektron einen Spin haben kann, der in Bezug auf die ausgewählte Raumachse nach oben oder unten gerichtet ist. Der Elektronenspin ist eine beobachtete Größe, da das Elektron ein schwaches Magnetfeld erzeugt, ähnlich dem Feld eines Magnetstabs. Dann bedeutet ein Spin nach oben, dass der Nordpol des Elektrons nach unten zeigt, und ein Spin nach unten bedeutet, dass der Nordpol nach oben schaut. Zwei Elektronen können in einen konjugierten Quantenzustand versetzt werden, in dem einer von ihnen einen nach oben und der andere nach unten gerichteten Spin aufweist, aber es ist unmöglich zu sagen, welches der Elektronen welchen Spin hat. Tatsächlich befinden sich im Grundzustand eines Heliumatoms zwei Elektronen in genau einem solchen Zustand, der als Spin-Singulett bezeichnet wird, da der Gesamtspin beider Elektronen gleich Null ist. Wenn wir diese beiden Elektronen trennen, ohne ihre Spins zu ändern, können wir weiterhin behaupten, dass sie zusammen Spin-Singulett sind, aber wir können immer noch nicht sagen, wie der Spin jedes einzelnen von ihnen einzeln sein wird. Wenn wir nun einen ihrer Drehungen messen und feststellen, dass er nach oben gerichtet ist, sind wir völlig sicher, dass der zweite nach unten gerichtet ist. In dieser Situation sagen wir, dass die Rücken verwickelt sind - nicht einer an sich hat eine bestimmte Bedeutung, während sie sich zusammen in einem bestimmten Quantenzustand befinden.
Einstein war sehr besorgt über das Phänomen der Verschränkung: Es schien die Grundprinzipien der Relativitätstheorie zu bedrohen. Betrachten wir den Fall zweier Elektronen in einem Spin-Singulett-Zustand, wenn sie im Raum weit voneinander entfernt sind. Lassen Sie einen von ihnen Alice und den anderen Bob nehmen. Angenommen, Alice hat den Spin ihres Elektrons gemessen und festgestellt, dass er nach oben gerichtet ist, und Bob hat nichts gemessen. Bis Alice ihre Messung abgeschlossen hatte, war es unmöglich zu sagen, wie der Spin seines Elektrons war. Aber sobald sie ihre Messung abgeschlossen hatte, wusste sie absolut, dass der Spin von Bobs Elektron nach unten gerichtet ist (in die Richtung, die dem Spin ihres eigenen Elektrons entgegengesetzt ist). Bedeutet dies, dass ihre Messung Bobs Elektron sofort in den Zustand versetzt, in dem sein Spin nach unten gerichtet ist? Wie könnte dies passieren, wenn die Elektronen räumlich getrennt sind? Einstein und seine Mitarbeiter Nathan Rosen und Boris Podolsky waren der Ansicht, dass die Geschichte der Messung verschränkter Systeme so ernst war, dass sie die Existenz der Quantenmechanik bedrohte. Das von ihnen formulierte Einstein-Podolsky-Rosen-Paradoxon (EPR) verwendet ein Gedankenexperiment ähnlich dem, das wir gerade beschrieben haben, um zu folgern: Die Quantenmechanik kann keine vollständige Beschreibung der Realität sein. Basierend auf den folgenden theoretischen Untersuchungen und vielen Messungen wurde nun eine gemeinsame Meinung aufgestellt, dass das EPR-Paradoxon einen Fehler enthält und die Quantentheorie korrekt ist. Die quantenmechanische Verschränkung ist real: Messungen verschränkter Systeme korrelieren, selbst wenn diese Systeme räumlich und zeitlich weit voneinander entfernt sind.
Kehren wir zu der Situation zurück, in der wir zwei Elektronen in einen Spin-Singulett-Zustand versetzen und sie an Alice und Bob verteilen. Was können wir über Elektronen sagen, bevor Messungen durchgeführt werden? Dass beide zusammen in einem bestimmten Quantenzustand sind (Spin-Singulett). Es ist ebenso wahrscheinlich, dass der Spin des Alicin-Elektrons nach oben oder unten gerichtet ist. Genauer gesagt kann der Quantenzustand seines Elektrons mit der gleichen Wahrscheinlichkeit der eine (Spin-up) oder der andere (Spin-down) sein. Für uns hat das Konzept der Wahrscheinlichkeit eine tiefere Bedeutung als zuvor. Zuvor haben wir einen bestimmten Quantenzustand (den Grundzustand eines Wasserstoffatoms) betrachtet und festgestellt, dass es einige „unangenehme“ Fragen gibt, z. B. „Wo befindet sich das Elektron?“, Fragen, deren Antworten nur im probabilistischen Sinne existieren. Wenn wir „gute“ Fragen stellen würden, zum Beispiel: „Was ist die Energie dieses Elektrons?“, Würden wir bestimmte Antworten darauf erhalten. Jetzt gibt es keine "guten" Fragen, die wir über Alices Elektron stellen könnten, deren Antworten nicht von Bobs Elektron abhängen würden. (Wir sprechen nicht über dumme Fragen wie "Hat Alices Elektron überhaupt einen Spin?" - Fragen, auf die es nur eine Antwort gibt.) Daher müssen wir probabilistische Sprache verwenden, um die Parameter eines der halb verwirrten Systeme zu bestimmen. Gewissheit entsteht nur, wenn wir den Zusammenhang zwischen Fragen betrachten, die Alice und Bob über ihre Elektronen stellen können.
Wir haben absichtlich mit einem der einfachsten quantenmechanischen Systeme begonnen, die wir kennen: den Spinsystemen einzelner Elektronen. Es ist zu hoffen, dass Quantencomputer auf der Basis derart einfacher Systeme gebaut werden. Das Spinsystem einzelner Elektronen oder anderer äquivalenter Quantensysteme wird jetzt Qubits genannt (kurz für "Quantenbits"), was ihre Rolle in Quantencomputern betont, ähnlich der Rolle, die gewöhnliche Bits in digitalen Computern spielen.
Stellen Sie sich jetzt vor, wir hätten jedes Elektron durch ein viel komplexeres Quantensystem mit vielen und nicht nur zwei Quantenzuständen ersetzt. Zum Beispiel gaben sie Alice und Bob Riegel aus reinem Magnesium. Bevor Alice und Bob getrennte Wege in verschiedene Richtungen gehen, können ihre Balken interagieren, und wir werden uns einig sein, dass sie dabei einen bestimmten allgemeinen Quantenzustand erreichen. Sobald Alice und Bob auseinander gehen, hören ihre Magnesiumriegel auf zu interagieren. Wie im Fall von Elektronen befindet sich jeder Balken in einem unbestimmten Quantenzustand, obwohl sie zusammen, wie wir glauben, einen vollständig bestimmten Zustand bilden. (In dieser Diskussion nehmen wir an, dass Alice und Bob in der Lage sind, ihre Magnesiumstäbe zu bewegen, ohne ihren inneren Zustand zu stören, so wie wir zuvor angenommen haben, dass Alice und Bob ihre verschränkten Elektronen trennen könnten, ohne ihre Spins zu ändern.) Aber der Unterschied Zwischen diesem Gedankenexperiment und dem Experiment mit Elektronen liegt die Unsicherheit im Quantenzustand jedes Balkens enorm. Ein Balken kann durchaus mehr Quantenzustände annehmen als die Anzahl der Atome im Universum. Hier kommt die Thermodynamik ins Spiel. Sehr ungenau definierte Systeme können jedoch einige genau definierte makroskopische Eigenschaften aufweisen. Eine solche Eigenschaft ist beispielsweise die Temperatur. Die Temperatur ist ein Maß für die Wahrscheinlichkeit, mit der ein Teil eines Systems eine bestimmte durchschnittliche Energie aufweist, wobei eine höhere Temperatur einer höheren Wahrscheinlichkeit entspricht, mehr Energie zu haben. Ein weiterer thermodynamischer Parameter ist die Entropie, die im Wesentlichen dem Logarithmus der Anzahl der Zustände entspricht, die das System annehmen kann. Eine weitere thermodynamische Eigenschaft, die für einen Magnesiumstab von Bedeutung wäre, ist seine Gesamtmagnetisierung, dh im Wesentlichen ein Parameter, der zeigt, wie viel mehr Elektronen sich im Stab befinden können, wenn der Spin nach oben zeigt, als wenn der Spin nach unten zeigt.
Wir haben die Thermodynamik in unsere Geschichte einbezogen, um Systeme zu beschreiben, deren Quantenzustände aufgrund ihrer Verschränkung mit anderen Systemen nicht genau bekannt sind. Die Thermodynamik ist ein leistungsfähiges Werkzeug zur Analyse solcher Systeme, aber ihre Entwickler haben eine solche Anwendung überhaupt nicht erwartet. Sadi Carnot, James Joule und Rudolph Clausius waren die Führer der industriellen Revolution des 19. Jahrhunderts und interessierten sich für ihre praktischste aller Fragen: Wie funktionieren Motoren? Druck, Volumen, Temperatur und Wärme sind das Fleisch und Blut von Motoren. Carnot stellte fest, dass Energie in Form von Wärme niemals vollständig in nützliche Arbeit wie das Heben von Gütern umgewandelt werden kann. Ein Teil der Energie wird immer verschwendet. Clausius leistete den Hauptbeitrag zur Schaffung der Idee der Entropie als universelles Werkzeug zur Bestimmung der Energieverluste während eines mit Wärme verbundenen Prozesses. Seine Hauptleistung war die Erkenntnis, dass die Entropie niemals abnimmt - in fast allen Prozessen wächst sie. Prozesse, bei denen die Entropie zunimmt, werden als irreversibel bezeichnet - gerade weil sie sich nicht umkehren können, ohne die Entropie zu verringern. Der nächste Schritt in der Entwicklung der statistischen Mechanik wurde von Clausius, Maxwell und Ludwig Boltzmann (unter anderem) gemacht - sie zeigten, dass Entropie ein Maß für Störung ist. Normalerweise, je mehr Sie auf etwas einwirken, desto mehr versauen Sie dort. Und selbst wenn Sie einen Prozess entwickelt haben, dessen Ziel es ist, die Ordnung wiederherzustellen, bildet sich dabei zwangsläufig mehr Entropie als sie zerstört wird, beispielsweise wenn Wärme freigesetzt wird. Der Kran, der die Stahlträger in perfekter Reihenfolge stapelt, schafft Ordnung in Bezug auf die Position der Träger, aber während seines Betriebs wird so viel Wärme freigesetzt, dass die gesamte Entropie immer noch wächst.
Dennoch ist der Unterschied zwischen der Sicht auf die Thermodynamik der Physiker des 19. Jahrhunderts und der Sicht der Quantenverschränkung nicht so groß, wie es scheint. Jedes Mal, wenn ein System mit einem externen Agenten interagiert, wird sein Quantenzustand mit dem Quantenzustand des Agenten verwechselt. Normalerweise führt diese Verschränkung zu einer Zunahme der Unsicherheit des Quantenzustands des Systems, mit anderen Worten zu einer Zunahme der Anzahl von Quantenzuständen, in denen sich das System befinden kann. Infolge der Wechselwirkung mit anderen Systemen wächst normalerweise die Entropie, definiert als Menge der dem System zur Verfügung stehenden Quantenzustände.
Im Allgemeinen bietet die Quantenmechanik eine neue Möglichkeit, physikalische Systeme zu charakterisieren, bei denen einige Parameter (z. B. Position im Raum) unsicher werden, während andere (z. B. Energie) häufig genau bekannt sind. Im Fall der Quantenverschränkung haben zwei grundlegend getrennte Teile des Systems einen bekannten gemeinsamen Quantenzustand, und jeder Teil separat ist ein unbestimmter Zustand. Ein Standardbeispiel für eine Verschränkung ist ein Paar von Drehungen in einem Singulettzustand, in dem es unmöglich ist zu sagen, welcher Dreh nach oben und welcher nach unten gerichtet ist. , , , , .
, , , , . — , , , 2π. , , , ‑. , , , . : - ? , , , . , , 6 . , ( , ) . , 1,5 , . , , , , ; , , . , , . ( « , …», , , , .) , , : , , , , , , . , , , , , , , , . : ! , , , , , . , , , , , , . , -. , , - , .
, - , - . , , - : , . , , , , -, . , - , (, , , ). -, , , , , . - , . , 60 . , , ( ) ,
Abb. 7.1. , a . , , t = 0. , t = 0 . , ‑.
, , « ». ? ? , . , , , . — , — , , . -, , ‑. - , , . , !
, , , — , , . «» , «», , , . 2, , , , . , , . , , ? , . , ? , , , . , , .