☦️ ⬛️ 🐣 Informationsentropie des Chaos 📃 👩🏼‍💻 👉🏽

Einführung

Es gibt viele Veröffentlichungen über Habr, die das Konzept der Entropie diskutieren, hier nur einige davon [1 ÷ 5]. Die Publikationen wurden von den Lesern positiv aufgenommen und stießen auf großes Interesse. Es reicht aus, die vom Autor der Veröffentlichung [1] angegebene Definition der Entropie anzugeben: „Entropie gibt an, wie viele Informationen Sie nicht über das System wissen.“ Veröffentlichungen über das Chaos-Phänomen auf Habr sind ebenfalls ausreichend [6–9]. Das Verhältnis von Entropie und Chaos in beiden Publikationsgruppen wurde jedoch nicht berücksichtigt.

Dies liegt an der Tatsache, dass unterschiedliche Wissensbereiche unterschiedliche Arten von Chaosmaßstäben unterscheiden:

informativ;
thermodynamisch;
Differential;
kulturell.

Chaosmaßnahmen werden auch unter Berücksichtigung ihrer Spezifität beschrieben, selbst in einem dieser Bereiche ist dies recht schwierig.

Um die Aufgabe so weit wie möglich zu vereinfachen, habe ich mich entschlossen, die Beziehung zwischen Informationsentropie und Chaos am Beispiel der Ähnlichkeit der Übergangsbereiche von Ordnung zu Chaos in den Diagrammen in Form von Punktabbildungen und in den Diagrammen des Entropiekoeffizienten für diese Regionen zu betrachten.

Was dabei herausgekommen ist, erfahren Sie, wenn Sie unter die Katze schauen.

Die Mechanismen des Übergangs von Ordnung zu Chaos

Eine Analyse der Mechanismen des Übergangs von der Ordnung zum Chaos in realen Systemen und verschiedenen Modellen hat die Vielseitigkeit relativ weniger Szenarien des Übergangs zum Chaos gezeigt. Der Übergang zum Chaos kann in Form eines Bifurkationsdiagramms dargestellt werden (der Begriff „Bifurkation“ bezeichnet qualitative Umlagerungen des Systems mit der Entstehung einer neuen Art seines Verhaltens).

Der Eintritt des Systems in den unvorhersehbaren Modus wird durch eine Kaskade von Gabelungen beschrieben, die nacheinander folgen. Die Kaskade von Bifurkationen führt nacheinander zu einer Wahl zwischen zwei Lösungen, dann vier usw. Das System beginnt in einem chaotischen, turbulenten Modus zu schwingen, bei dem die Anzahl der möglichen Werte nacheinander verdoppelt wird.

Wir betrachten Verzweigungen der Periodenverdopplung und das Auftreten von Chaos in Punktzuordnungen. Die Anzeige ist eine Funktion, die die Abhängigkeit der folgenden Werte der Systemparameter von vorherigen Werten anzeigt:

x_{n + 1} = f (x_{n}) = l a m b d a x_{n} (1 - x_{n})

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$

Betrachten Sie auch die zweite häufig verwendete Funktion:

x_{n + 1} = f (x_{n}) = l a m b d a c d o t x_{n} c d o t (1 - x_{n}^{2})

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Mithilfe von Punktzuordnungen werden Objekte nicht kontinuierlich, sondern zeitdiskret untersucht . Beim Übergang zur Anzeige kann sich die Dimension des untersuchten Systems verringern.

Beim Ändern des externen Parameters \ lambda zeigen Punktzuordnungen ein ziemlich kompliziertes Verhalten, das bei ausreichend großem \ lambda chaotisch wird. Chaos ist eine sehr schnelle Rezession von Flugbahnen im Phasenraum.

Bifurkation ist eine qualitative Umstrukturierung des Films. Die Werte des Steuerparameters, bei denen Bifurkationen auftreten, werden als kritische Werte oder Bifurkationswerte bezeichnet.

Um die Diagramme zu erstellen, verwenden wir die folgenden zwei Auflistungen:

Nr. 1. Für die Funktion:

x_{n + 1} = f (x_{n}) = l a m b d a x_{n} (1 - x_{n})

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$

Programmliste

# -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=(a-1)/a#     def ff(x):#  return a*x*(1-x) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

Nr. 2. Für die Funktion

x_{n + 1} = f (x_{n}) = l a m b d a c d o t x_{n} c d o t (1 - x_{n}^{2})

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Programmliste

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=((a-1)/a)**0.5 def ff(x):#  return a*x*(1-x**2) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n}^{2})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

Bewertung der Auswirkungen der Art der logistischen Funktion auf kritische Werte

l a m b d a

$\ lambda$ Betrachten Sie Diagramme mit einer Funktion

x_{n + 1} = f (x_{n}) = l a m b d a x_{n} (1 - x_{n})

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ Hierfür verwenden wir Listing Nr. 1:

Für 0 <\ lambda <1 für

l a m b d a = $ 0, 9

$\ lambda = $ 0,9$ und x0 = 0,47 erhalten wir das Diagramm:

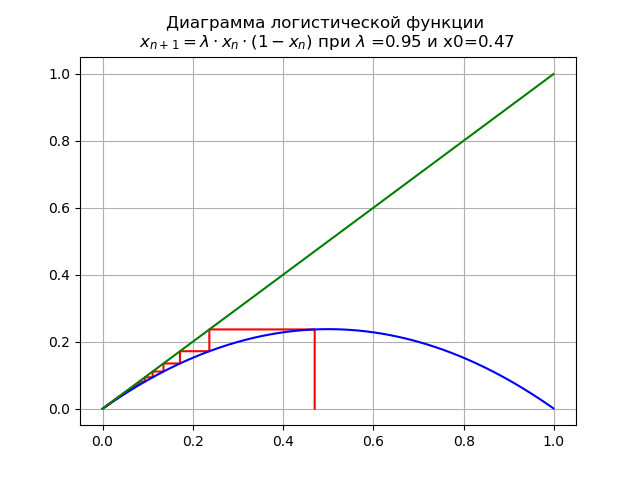
In diesem Fall hat die Karte einen einzelnen festen Punkt

x^{*} = 0

$x ^ {*} = 0$
das ist nachhaltig.

Bei

1 < l a m b d a < 3

$1 <\ lambda <3$ für

l a m b d a = $ 2,

$\ lambda = $ 2,$ x0 = 0,7 wir erhalten das Diagramm:

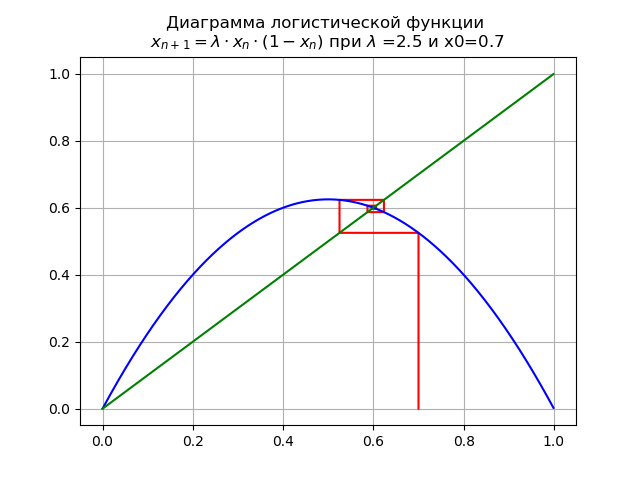
Auf dem Segment [0, 1] erscheint ein weiterer fester Fixpunkt

x_{1}^{*} = 1 - 1 / l a m b d a

$x_ {1} ^ {*} = 1-1 / \ lambda$

Bei

1 < l a m b d a < 3

$1 <\ lambda <3$ für

l a m b d a = $ 2,

$\ lambda = $ 2,$ und x0 = 0,01 erhalten wir das Diagramm:

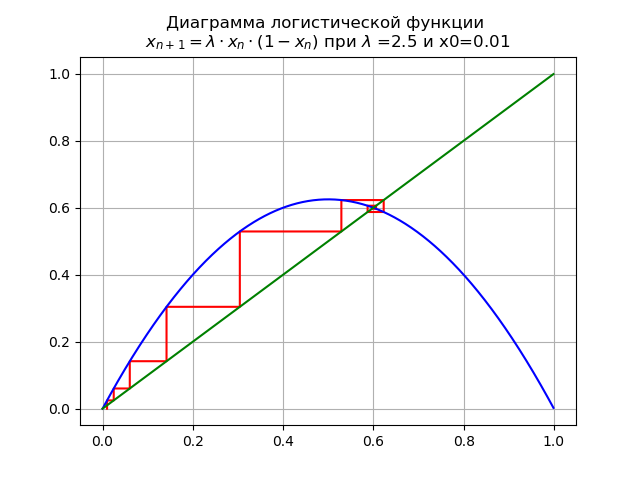
Fixpunkt

x^{*} = 0

$x ^ {*} = 0$ verliert an Stabilität.

Bei

3 < l a m b d a < 3, 45

$3 <\ lambda <3,45$ für

l a m b d a = $ 3.4

$\ lambda = $ 3.4$ und x0 = 0,7 erhalten wir das Diagramm:

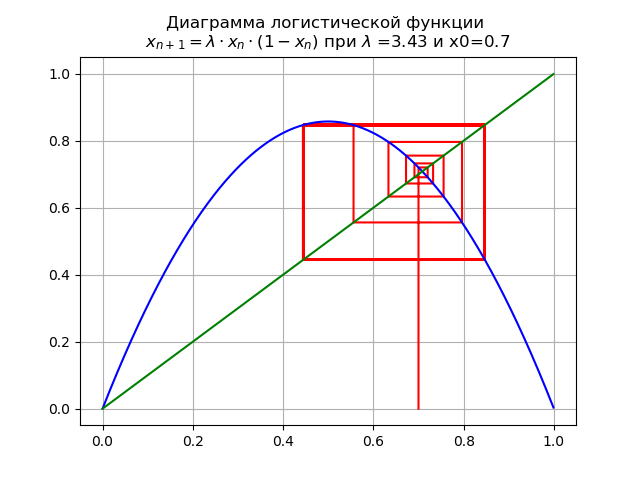
Das Mapping erfährt eine Bifurkation: Fixpunkt

x_{1}^{*}

$x_ {1} ^ {*}$ wird instabil und stattdessen erscheint ein Doppelzyklus.

Bei

3.45 < l a m b d a < 4.0

$3.45 <\ lambda <4.0$ für

l a m b d a = $ 3, 5

$\ lambda = $ 3,5$
und x0 = 0,2 erhalten wir das Diagramm:

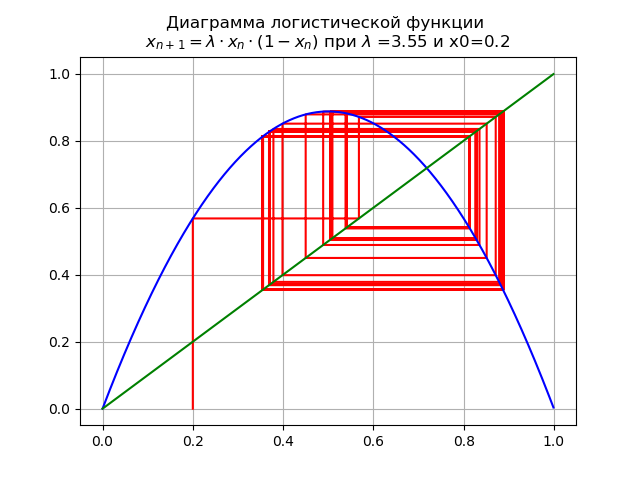
Beim Übergeben eines Parameters

l a m b d a

$\ lambda$ durch Wert

l a m b d a = 3, 45

$\ lambda = 3,45$ Ein 2-facher Zyklus wird zu einem 4-fachen und darüber hinaus.

Zum Endwert

l a m b d a = 4

$\ lambda = 4$ Das System hat instabile Zyklen aller möglichen Aufträge:

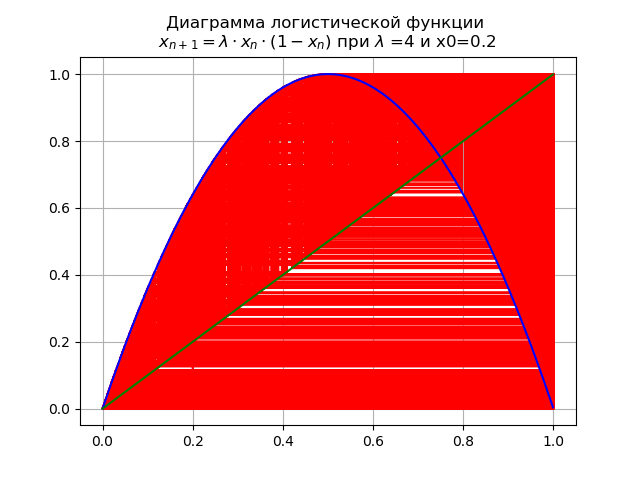
Bewertung der Auswirkungen der Art der logistischen Funktion auf kritische Werte

l a m b d a

$\ lambda$ Betrachten Sie Diagramme mit einer Funktion

x_{n + 1} = f (x_{n}) = l a m b d a c d o t x_{n} c d o t (1 - x_{n}^{2})

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$ , hierfür verwenden wir Listing Nr. 2.

Bei

0 < l a m b d a <= 1, 0

$0 <\ lambda <= 1,0$ für

l a m b d a = 0, 5

$\ lambda = 0,5$ und x0 = 0,2:

Das Mapping hat einen einzelnen Fixpunkt

x^{*} = 0

$x ^ {*} = 0$ das ist nachhaltig.

Bei

1 < l a m b d a <= 1, 998 . . .

$1 <\ lambda <= 1,998 ...$ für

l a m b d a = $ 1,

$\ lambda = $ 1,$ und x0 = 0,55:

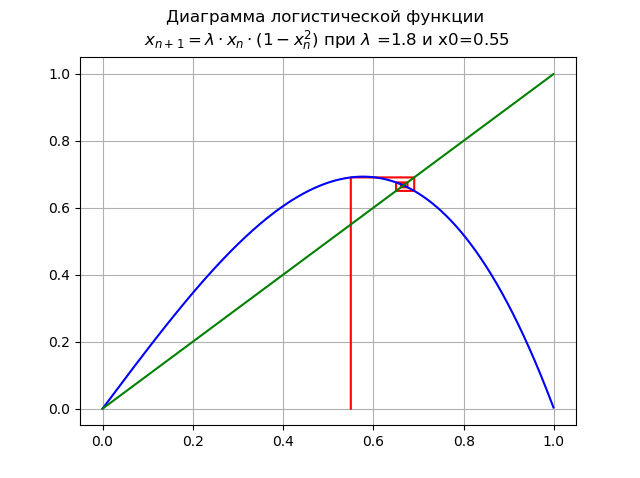
Punkt

x^{*} = 0

$x ^ {*} = 0$ verliert an Stabilität, erscheint ein neuer stabiler Punkt

x_{1}^{*}

$x_ {1} ^ {*}$

Bei

1.99 < l a m b d a <= 2.235 . . .

$1.99 <\ lambda <= 2.235 ...$ für

l a m b d a = $ 2.

$\ lambda = $ 2.$ und x0 = 0,2:

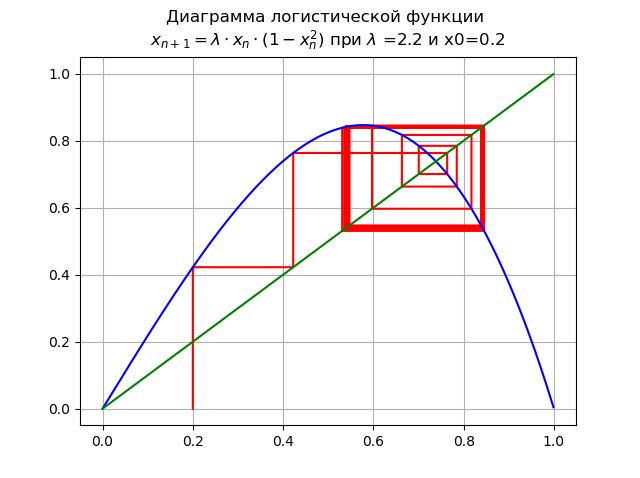
Wenn eine Bifurkation der Verdoppelung der Periode auftritt, erscheint ein zweifacher Zyklus. Weitere Erhöhung

l a m b d a

$\ lambda$ führt zu einer Kaskade von Periodenverdopplungsgabelungen.

Bei

2, 235 < l a m b d a 2, 5980 . . .

$2,235 <\ lambda 2,5980 ...$ für

l a m b d a = 2.287

$\ lambda = 2.287$ und x0 = 0,2:

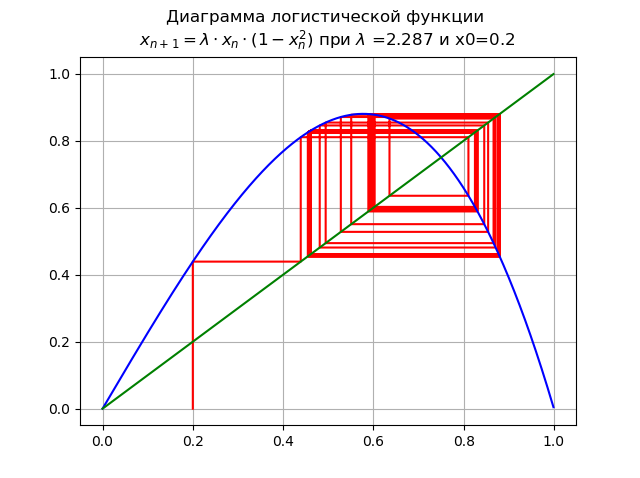
Erhöhen

l a m b d a

$\ lambda$ führte zu einer Kaskade von Periodenverdopplungen.

Bei

l a m b d a = 2, 59

$\ lambda = 2,59$ Das System hat instabile Zyklen aller möglichen Zeiträume:

Wie in den Diagrammen gezeigt, ist mit zunehmender Reihenfolge der logistischen Funktion der Bereich

$\ lambda$ verjüngt sich.

Mithilfe von Diagrammen haben wir den Pfad von der Reihenfolge zum Chaos verfolgt und dabei die Werte festgelegt

l a m b d a

$\ lambda$ für verschiedene logistische Funktionen. Es bleibt die Frage zu beantworten: Wie kann man das Chaos messen? Die Antwort auf einige der am Anfang des Artikels aufgeführten Arten von Chaos ist bekannt
- Entropie ist ein Maß für Chaos. Diese Antwort kann vollständig auf das Informationschaos zurückgeführt werden. Welche Entropie wird hier angewendet und wie kann man sie mit dem bereits berücksichtigten numerischen Wert vergleichen?

l a m b d a

$\ lambda$ - Ich werde versuchen, diese Frage im nächsten Teil des Artikels zu beantworten.

Informationsentropie und Entropiekoeffizient

Wir werden die binäre Informationsentropie für unabhängige zufällige Ereignisse betrachten.

x

$x$ c

n

$n$ mögliche Zustände mit Wahrscheinlichkeiten verteilt

p_{i} (i = 1, . ., n)

$p_ {i} (i = 1, .., n)$ . Die binäre Informationsentropie wird nach folgender Formel berechnet:

H (x) = - s u m_{i = 1}^{n} p_{i} c d o t l o g_{2} (p_{i})

$H (x) = - \ sum_ {i = 1} ^ {n} p_ {i} \ cdot log_ {2} (p_ {i})$

Dieser Wert wird auch als mittlere Entropie der Nachricht bezeichnet. Wert

H_{i} = - l o g_{2} (p_{i})

$H_ {i} = - log_ {2} (p_ {i})$ private Entropie genannt, die nur den i- ten Zustand charakterisiert. Im allgemeinen Fall kann die Basis des Logarithmus in der Definition der Entropie größer als 1 sein; seine Wahl bestimmt die Maßeinheit der Entropie.

Wir werden dezimale Logarithmen verwenden, bei denen Entropie und Information in Bits gemessen werden. Die Informationsmenge in Bits wird korrekt berechnet, wenn beispielsweise Variablen verwendet werden

X

$X$ und

D e l t a

$\ Delta$ wird in die entsprechenden Ausdrücke für Entropie eingesetzt, egal in welcher, aber immer in den gleichen Einheiten. In der Tat:

q = H (x) - H (D e l t a) = l o g_{10} l e f t (X_{2} - X_{1} r i g h t) - l o g_{10} (2 D e l t a) = l o g_{10} (f r a c X_{2} - X_{1} 2 D e l t a)

$q = H (x) -H (\ Delta) = log_ {10} \ left (X_ {2} -X_ {1} \ right) -log_ {10} (2 \ Delta) = log_ {10} (\ frac {X_ {2} -X_ {1}} {2 \ Delta})$

wo X und

D e l t a

$\ Delta$ muss in den gleichen Einheiten sein.

Eine Schätzung des Entropiewertes einer Zufallsvariablen aus experimentellen Daten ergibt sich aus einem Histogramm aus der folgenden Beziehung:

D e l t a_{e} = f r a c 12 e^{H (x)} = f r a c d 2 p r o d_{i = 1}^{m} (f r a c n n_{i})^{f r a c n_{i} n} = f r a c d n 2 10^{- f r a c 1 n} s u m_{i = 1}^{m} n_{i} l o g_{10} (n_{i})

$\ Delta_ {e} = \ frac {1} {2} e ^ {H (x)} = \ frac {d} {2} \ prod_ {i = 1} ^ {m} (\ frac {n} { n_ {i}}) ^ {\ frac {n_ {i}} {n}} = \ frac {dn} {2} 10 ^ {- \ frac {1} {n}} \ sum_ {i = 1} ^ {m} n_ {i} log_ {10} (n_ {i})$

wo:

d

$d$ –Breite jeder Spalte des Histogramms;

m

$m$ - Anzahl der Spalten;

n

$n$ -Gesamte Datenmenge;

n_{i}

$n_ {i}$ - Datenmenge in

i

$i$ diese Spalte.

Der Entropiekoeffizient wird aus dem Verhältnis bestimmt:

k_{e} = f r a c D e l t a_{e} s i g m a

$k_ {e} = \ frac {\ Delta_ {e}} {\ sigma}$

wo:

s i g m a

$\ sigma$ - Standardabweichung.

Informationsentropie als Maß für Chaos

Um die Phänomene des Informationschaos anhand des Entropiekoeffizienten zu analysieren, erstellen wir zunächst ein Verzweigungsdiagramm für die Funktion

x_{n + 1} = f (x_{n}) = l a m b d a x_{n} (1 - x_{n})

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ mit der Anwendung von Übergangsbereichen, die bei der Erstellung von Histogrammen erhalten wurden:

Verzweigungsdiagramm

 import matplotlib.pyplot as plt import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(3.58,3.9,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   3,6<= $\lambda$ <=3,9") plt.xlabel("r") plt.ylabel("$\lambda$ ") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()

Wir bekommen:

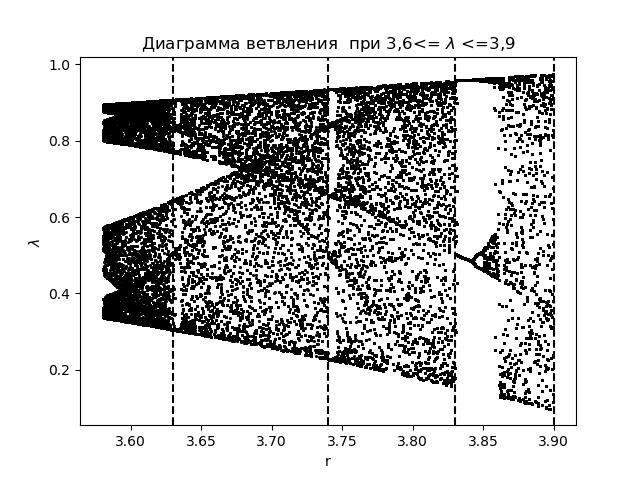
Wir zeichnen für den Entropiekoeffizienten für die gleichen Bereiche

l a m b d a

$\ lambda$ ::

Der Graph für den Entropiekoeffizienten

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(3.58,3.9,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-M[i-1,j]) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.title("  ke  3,6<= $\lambda$ <=3,9") plt.plot(arange(3.58,3.9,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.grid() plt.show()

Wir bekommen:

Beim Vergleich des Diagramms und des Diagramms sehen wir eine identische Anzeige der Bereiche im Diagramm und im Diagramm für den Entropiekoeffizienten für die Funktion

x_{n + 1} = f (x_{n}) = l a m b d a x_{n} (1 - x_{n})

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ .

Zur weiteren Analyse der Phänomene des Informationschaos anhand des Entropiekoeffizienten erstellen wir ein Verzweigungsdiagramm für die logistische Funktion:

x_{n + 1} = f (x_{n}) = l a m b d a c d o t x_{n} c d o t (1 - x_{n}^{2})

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$ mit der Anwendung von Übergangsbereichen:

Verzweigungsdiagramm

 import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.25,2.56,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-(y[n-1])**2),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   2.25<=$\lambda$ <=2.56") plt.xlabel("$\lambda$ ") plt.ylabel("y") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.show()

Wir bekommen:

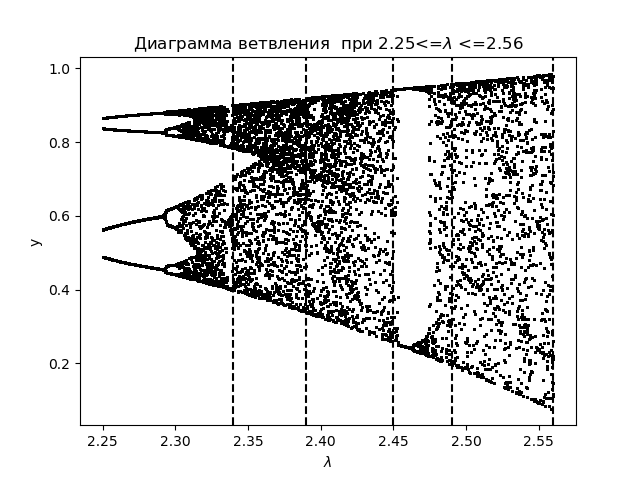
Wir zeichnen für den Entropiekoeffizienten für die gleichen Bereiche

l a m b d a

$\ lambda$ ::

Entropiekoeffizientendiagramm

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(2.25,2.56,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-(M[i-1,j])**2) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.figure(2) plt.title("  ke  2.25<= $\lambda$ <=2.56") plt.plot(arange(2.25,2.56,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.grid() plt.show()

Wir bekommen:

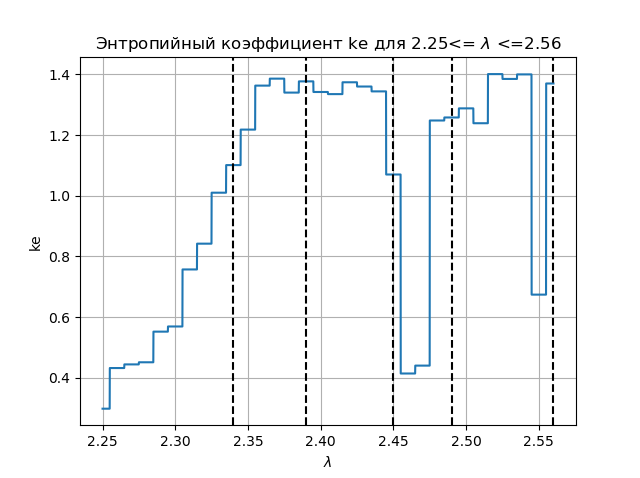
Beim Vergleich des Diagramms und des Diagramms sehen wir eine identische Anzeige der Bereiche im Diagramm und im Diagramm für den Entropiekoeffizienten für die Funktion

x_{n + 1} = f (x_{n}) = l a m b d a c d o t x_{n} c d o t (1 - x_{n}^{2})

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Schlussfolgerungen:

Das Bildungsproblem wird in dem Artikel gelöst: Ist die Informationsentropie ein Maß für das Chaos, und die Antwort auf diese Frage wird von Python bejaht.

Informationsentropie des Chaos

Einführung

Die Mechanismen des Übergangs von Ordnung zu Chaos

Informationsentropie und Entropiekoeffizient

Informationsentropie als Maß für Chaos

Schlussfolgerungen:

Referenzen

More articles: