Bilder aus groben Skizzen: Genau so funktioniert das neuronale Netzwerk NVIDIA GauGAN

Im vergangenen Monat stellte NVIDIA auf der NVIDIA GTC 2019 eine neue Anwendung vor, die vom Benutzer gezeichnete einfache farbige Kugeln in atemberaubende, fotorealistische Bilder verwandelt.


Die Anwendung basiert auf der Technologie generativ-wettbewerbsfähiger Netzwerke (GAN), die auf Deep Learning basiert. NVIDIA selbst nennt es GauGAN - ein Wortspiel, das sich auf den Künstler Paul Gauguin beziehen soll. Die GauGAN-Funktionalität basiert auf dem neuen SPADE-Algorithmus.

In diesem Artikel werde ich erklären, wie dieses technische Meisterwerk funktioniert. Und um so viele interessierte Leser wie möglich anzulocken, werde ich versuchen, eine detaillierte Beschreibung der Funktionsweise von Faltungs-Neuronalen Netzen zu geben. Da SPADE ein generativ-wettbewerbsfähiges Netzwerk ist, werde ich Ihnen mehr darüber erzählen. Wenn Sie mit diesem Begriff bereits vertraut sind, können Sie sofort zum Abschnitt „Bild-zu-Bild-Übertragung“ wechseln.

Bilderzeugung

Beginnen wir zu verstehen: In den meisten modernen Deep-Learning-Anwendungen wird der neuronale Diskriminantentyp (Diskriminator) verwendet, und SPADE ist ein generatives neuronales Netzwerk (Generator).

Diskriminatoren

Der Diskriminator klassifiziert die Eingabedaten. Beispielsweise ist ein Bildklassifizierer ein Diskriminator, der ein Bild aufnimmt und ein geeignetes Klassenetikett auswählt, beispielsweise das Bild als "Hund", "Auto" oder "Ampel" definiert, dh ein Etikett auswählt, das das gesamte Bild beschreibt. Die vom Klassifikator erhaltene Ausgabe wird normalerweise als Zahlenvektor dargestellt $$$v$wo $$$v_i$Ist eine Zahl von 0 bis 1, die das Vertrauen des Netzwerks ausdrückt, dass das Bild zu dem ausgewählten gehört $$$i$Klasse.

Der Diskriminator kann auch eine Liste von Klassifikationen zusammenstellen. Es kann jedes Pixel eines Bildes als zur Klasse der „Menschen“ oder „Maschinen“ gehörig klassifizieren (die sogenannte „semantische Segmentierung“).


Der Klassifizierer nimmt ein Bild mit 3 Kanälen (rot, grün und blau) auf und vergleicht es mit einem Konfidenzvektor in jeder möglichen Klasse, die das Bild darstellen kann.

Da die Verbindung zwischen dem Bild und seiner Klasse sehr komplex ist, durchlaufen neuronale Netze es durch einen Stapel von vielen Schichten, von denen jede es „leicht“ verarbeitet und seine Ausgabe auf die nächste Interpretationsebene überträgt.

Generatoren

Ein generatives Netzwerk wie SPADE empfängt einen Datensatz und versucht, neue Originaldaten zu erstellen, die so aussehen, als ob sie zu dieser Datenklasse gehören. Gleichzeitig können die Daten alles sein: Töne, Sprache oder etwas anderes, aber wir werden uns auf Bilder konzentrieren. Im Allgemeinen ist die Dateneingabe in ein solches Netzwerk einfach ein Vektor von Zufallszahlen, wobei jeder der möglichen Sätze von Eingabedaten ein eigenes Bild erzeugt.


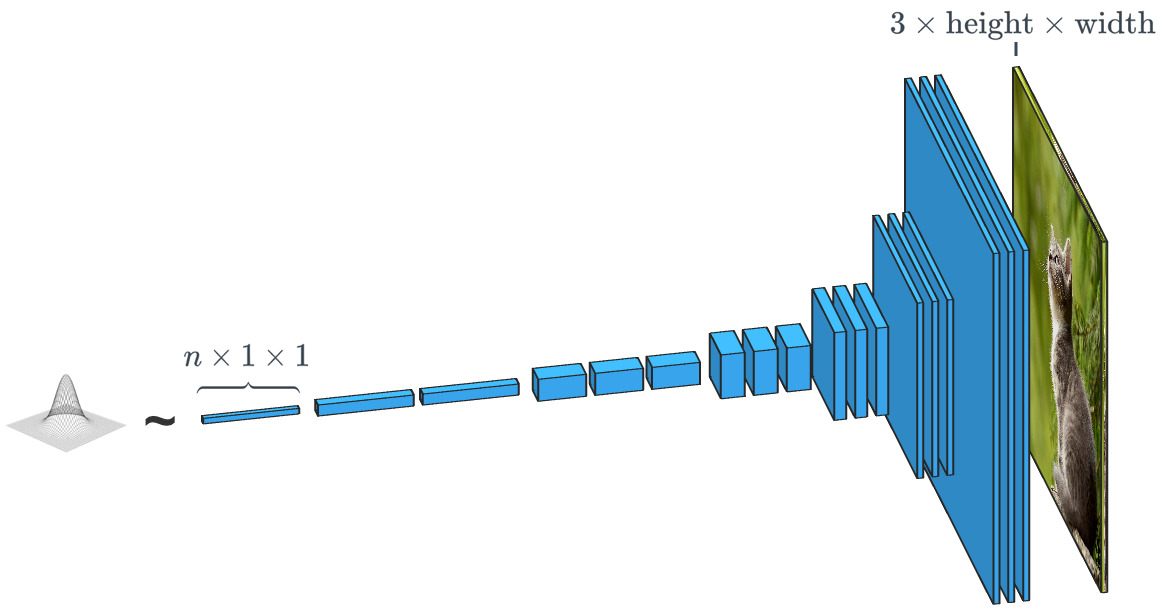Ein Generator, der auf einem zufälligen Eingabevektor basiert, arbeitet praktisch entgegengesetzt zum Bildklassifizierer. In "bedingten Klassen" -Generatoren ist der Eingabevektor tatsächlich der Vektor einer gesamten Datenklasse.

Wie wir bereits gesehen haben, verwendet SPADE viel mehr als nur einen „Zufallsvektor“. Das System wird von einer Art Zeichnung geleitet, die als "Segmentierungskarte" bezeichnet wird. Letzteres gibt an, was und wo gepostet werden soll. SPADE führt den Prozess entgegen der oben erwähnten semantischen Segmentierung durch. Im Allgemeinen hat eine diskriminierende Aufgabe, die einen Datentyp in einen anderen konvertiert, eine ähnliche Aufgabe, nimmt jedoch einen anderen, ungewöhnlichen Pfad.

Moderne Generatoren und Diskriminatoren verwenden normalerweise Faltungsnetzwerke, um ihre Daten zu verarbeiten. Eine umfassendere Einführung in Convolutional Neural Networks (CNNs) finden Sie im Beitrag Chew on Karna oder in der Arbeit von Andrei Karpati .

Es gibt einen wichtigen Unterschied zwischen dem Klassifikator und dem Bildgenerator, und er liegt darin, wie genau sie die Größe des Bildes während seiner Verarbeitung ändern. Der Bildklassifizierer sollte ihn reduzieren, bis das Bild alle räumlichen Informationen verliert und nur noch Klassen übrig sind. Dies kann durch Kombinieren von Schichten oder durch die Verwendung von Faltungsnetzwerken erreicht werden, durch die einzelne Pixel geleitet werden. Der Generator hingegen erzeugt ein Bild unter Verwendung des umgekehrten Prozesses der "Faltung", der als Faltungsumsetzung bezeichnet wird. Er wird oft mit "Entfaltung" oder "umgekehrter Faltung" verwechselt.


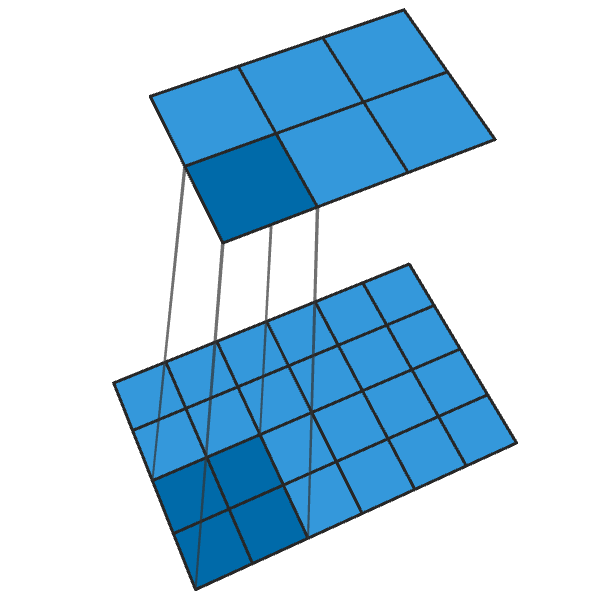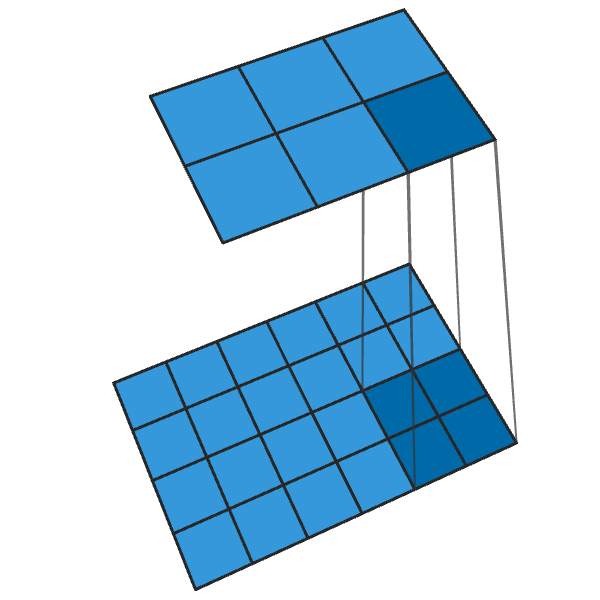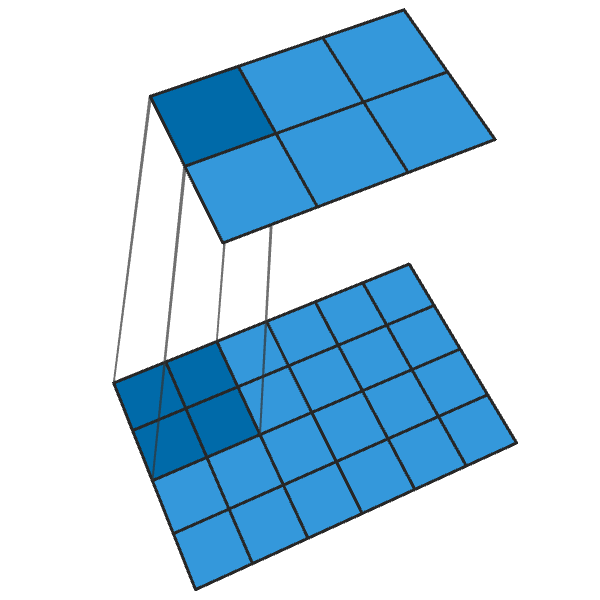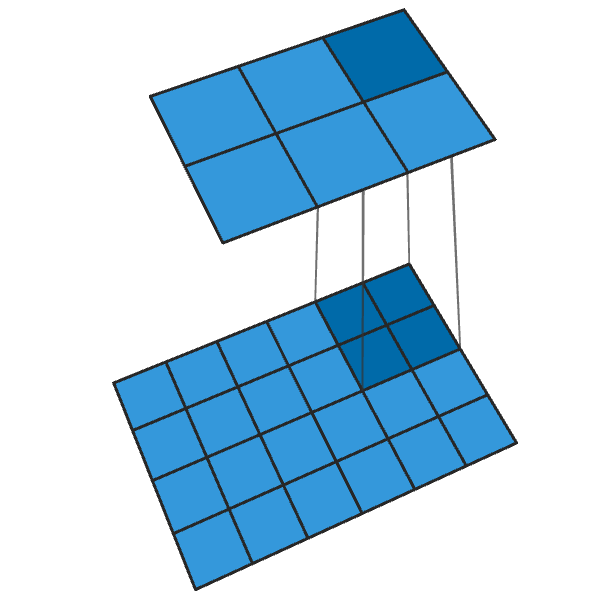
Herkömmliche 2x2-Faltung mit einem Schritt von „2“ verwandelt jeden 2x2-Block in einen Punkt und reduziert die Ausgabegröße um 1/2.


Eine transponierte 2x2-Faltung mit einem Schritt von "2" erzeugt von jedem Punkt einen 2x2-Block, wodurch die Ausgabegröße um das Zweifache erhöht wird.

Generator Training

Theoretisch kann ein Faltungs-Neuronales Netzwerk Bilder wie oben beschrieben erzeugen. Aber wie trainieren wir sie? Das heißt, wenn wir den Satz von Eingabebilddaten berücksichtigen, wie können wir die Parameter des Generators (in unserem Fall SPADE) so anpassen, dass neue Bilder erstellt werden, die so aussehen, als ob sie dem vorgeschlagenen Datensatz entsprechen?

Dazu müssen Sie mit Bildklassifizierern vergleichen, bei denen jeder die richtige Klassenbezeichnung hat. Wenn wir den Netzwerkvorhersagevektor und die richtige Klasse kennen, können wir den Backpropagation-Algorithmus verwenden, um die Netzwerkaktualisierungsparameter zu bestimmen. Dies ist notwendig, um die Genauigkeit bei der Bestimmung der gewünschten Klasse zu erhöhen und den Einfluss anderer Klassen zu verringern.


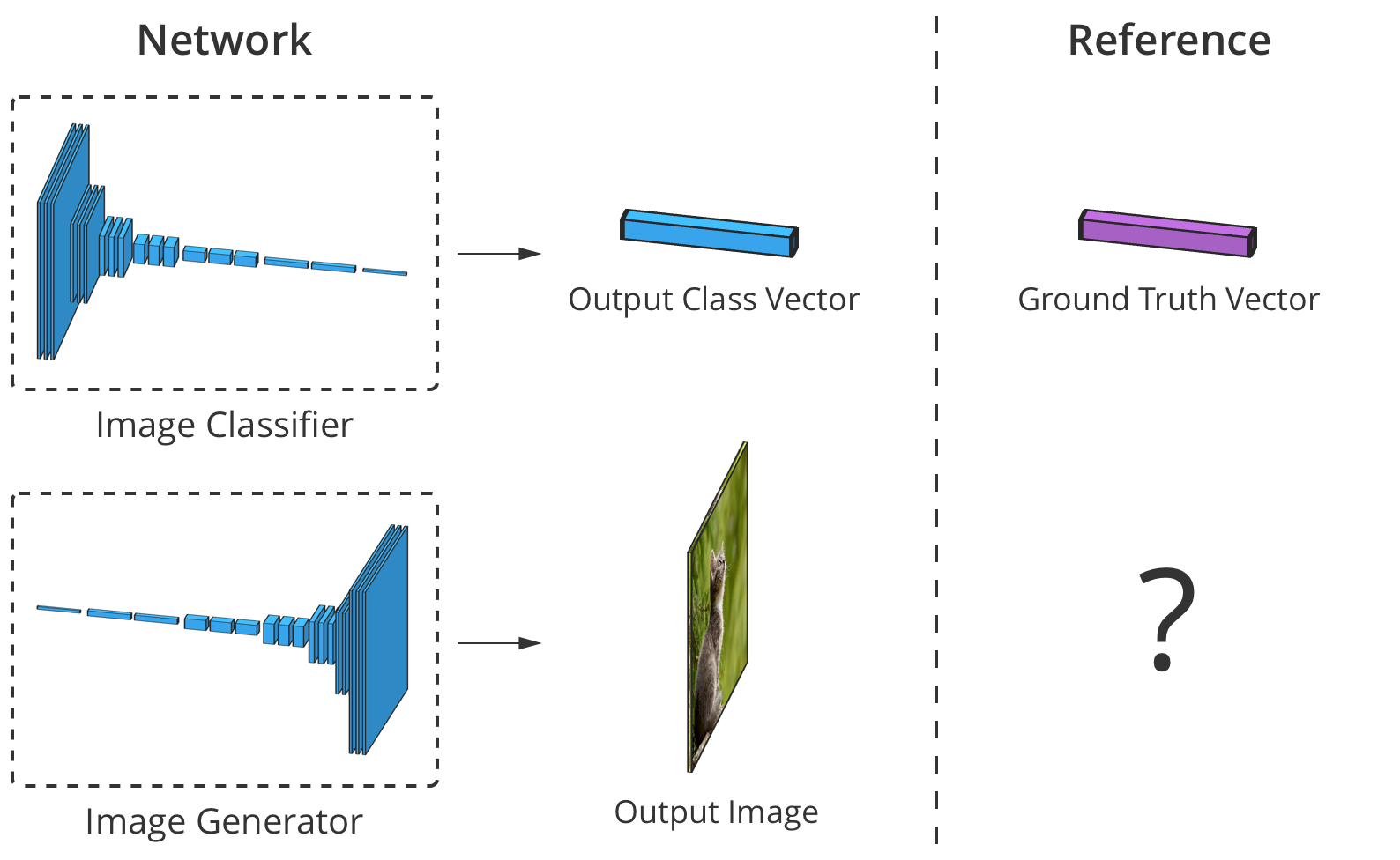Die Genauigkeit des Bildklassifizierers kann geschätzt werden, indem seine Ausgabe Element für Element mit dem richtigen Klassenvektor verglichen wird. Für Generatoren gibt es jedoch kein „richtiges“ Ausgabebild.

Das Problem ist, dass es beim Erstellen eines Bildes durch den Generator keine „richtigen“ Werte für jedes Pixel gibt (wir können das Ergebnis nicht vergleichen, wie im Fall eines Klassifikators, der auf einer zuvor vorbereiteten Basis basiert, ca. Trans.). Theoretisch ist jedes Bild gültig, das glaubwürdig und den Zieldaten ähnlich aussieht, auch wenn sich seine Pixelwerte stark von realen Bildern unterscheiden.

Wie können wir dem Generator also mitteilen, in welchen Pixeln er seine Ausgabe ändern soll und wie er realistischere Bilder erstellen kann (dh wie ein „Fehlersignal“ ausgegeben wird)? Die Forscher haben viel über diese Frage nachgedacht, und tatsächlich ist es ziemlich schwierig. Die meisten Ideen, wie die Berechnung einer durchschnittlichen „Entfernung“ zu realen Bildern, erzeugen verschwommene Bilder von schlechter Qualität.

Im Idealfall könnten wir mithilfe eines „High-Level“ -Konzepts „messen“, wie realistisch die generierten Bilder aussehen, z. B. „Wie schwierig ist es, dieses Bild vom realen zu unterscheiden?“ ...

Generative gegnerische Netzwerke

Genau dies wurde im Rahmen von Goodfellow et al., 2014, implementiert. Die Idee ist, Bilder mit zwei neuronalen Netzen anstelle von einem zu erzeugen: einem Netz -
Generator, der zweite ist ein Bildklassifikator (Diskriminator). Die Aufgabe des Diskriminators besteht darin, die Ausgabebilder des Generators von den realen Bildern aus dem Primärdatensatz zu unterscheiden (die Klassen dieser Bilder werden als "falsch" und "real" bezeichnet). Die Aufgabe des Generators besteht darin, den Diskriminator auszutricksen, indem Bilder erstellt werden, die den Bildern im Datensatz so ähnlich wie möglich sind. Wir können sagen, dass der Generator und der Diskriminator Gegner in diesem Prozess sind. Daher der Name: generativ-kontroverses Netzwerk .


Generativ-wettbewerbsfähiges Netzwerk basierend auf zufälliger Vektoreingabe. In diesem Beispiel versucht einer der Generatorausgänge, den Diskriminator dazu zu bringen, ein "echtes" Bild auszuwählen.

Wie hilft uns das? Jetzt können wir eine Fehlermeldung verwenden, die ausschließlich auf der Vorhersage des Diskriminators basiert: einen Wert von 0 ("falsch") bis 1 ("real"). Da der Diskriminator ein neuronales Netzwerk ist, können wir seine Schlussfolgerungen über Fehler mit dem Bildgenerator teilen. Das heißt, der Diskriminator kann dem Generator mitteilen, wo und wie er seine Bilder anpassen soll, um den Diskriminator besser zu „täuschen“ (dh wie der Realismus seiner Bilder erhöht werden kann).

Während des Lernens, wie man gefälschte Bilder findet, gibt der Diskriminator dem Generator ein immer besseres Feedback darüber, wie dieser seine Arbeit verbessern kann. Somit führt der Diskriminator eine "Lernverlust" -Funktion für den Generator aus.

Herrliche kleine GAN

Das von uns in seiner Arbeit berücksichtigte GAN folgt der oben beschriebenen Logik. Sein Diskriminator $$$D$analysiert das Bild $$$x$und bekommt den Wert $$$D (x)$von 0 bis 1, was sein Vertrauen widerspiegelt, dass das Bild vom Generator echt oder gefälscht ist. Sein Generator $$$G$erhält einen zufälligen Vektor normalverteilter Zahlen $$$Z$und zeigt das Bild an $$$G (z)$das kann vom Diskriminator ausgetrickst werden (in der Tat dieses Bild $$$D (G (z))$)

Eines der Themen, die wir nicht besprochen haben, ist die Schulung des GAN und die Verwendung von Verlustfunktionsentwicklern zur Messung der Netzwerkleistung. Im Allgemeinen sollte die Verlustfunktion mit dem Training des Diskriminators zunehmen und mit dem Training des Generators abnehmen. Die Verlustfunktion des Quell-GAN verwendete die folgenden zwei Parameter. Der erste ist
stellt den Grad dar, in dem der Diskriminator reale Bilder korrekt als real klassifiziert. Das zweite ist, wie gut der Diskriminator gefälschte Bilder erkennt:

$$$ inline $ \ begin {Gleichung *} \ mathcal {L} _ \ text {GAN} (D, G) = \ underbrace {E _ {\ vec {x} \ sim p_ \ text {data}} [\ log D ( \ vec {x})]} _ {\ text {Genauigkeit bei realen Bildern}} + \ underbrace {E _ {\ vec {z} \ sim \ mathcal {N}} [\ log (1 - D (G (\ vec {z}))]} _ {\ text {Genauigkeit bei Fälschungen}} \ end {Gleichung *} $ inline $

Diskriminator $$$D$leitet seine Behauptung ab, dass das Bild real ist. Es macht seitdem Sinn $$$LogD (x)$erhöht sich, wenn der Diskriminator x als real betrachtet. Wenn der Diskriminator gefälschte Bilder besser erkennt, steigt auch der Wert des Ausdrucks. $$$Log (1-D (G (z))$(beginnt nach 1 zu streben), da $$$D (G (z))$wird zu 0 tendieren.

In der Praxis bewerten wir die Genauigkeit anhand ganzer Bildstapel. Wir machen viele (aber keineswegs alle) echte Bilder $$$x$und viele zufällige Vektoren $$$Z$um die Durchschnittswerte gemäß der obigen Formel zu erhalten. Dann wählen wir häufige Fehler und einen Datensatz aus.

Dies führt im Laufe der Zeit zu interessanten Ergebnissen:

Goodfellow GAN simuliert MNIST-, TFD- und CIFAR-10-Datensätze. Konturbilder sind im Datensatz den benachbarten Fälschungen am nächsten.

Das alles war erst vor 4,5 Jahren fantastisch. Glücklicherweise schreitet das maschinelle Lernen, wie SPADE und andere Netzwerke zeigen, weiterhin rasant voran.

Trainingsprobleme

Generativ-wettbewerbsfähige Netzwerke sind bekannt für ihre Komplexität bei der Vorbereitung und Instabilität der Arbeit. Eines der Probleme besteht darin, dass, wenn der Generator im Trainingstempo dem Diskriminator zu weit voraus ist, seine Auswahl an Bildern auf diejenigen beschränkt wird, die ihm helfen, den Diskriminator zu täuschen. Infolgedessen kommt es beim Training des Generators darauf an, ein einziges universelles Bild zu erstellen, um den Diskriminator auszutricksen. Dieses Problem wird als "Kollapsmodus" bezeichnet.


Der GAN-Kollapsmodus ähnelt dem von Goodfellow. Bitte beachten Sie, dass viele dieser Schlafzimmerbilder einander sehr ähnlich sehen. Quelle

Ein weiteres Problem besteht darin, dass der Generator den Diskriminator effektiv austrickst $$$D (g (Z))$arbeitet daher mit einem sehr kleinen Gradienten $$$\ mathcal {L} _ \ text {GAN} G (\ vec {z})$Ich kann nicht genug Daten erhalten, um die wahre Antwort zu finden, in der dieses Bild realistischer aussehen würde.

Die Bemühungen der Forscher, diese Probleme zu lösen, zielten hauptsächlich darauf ab, die Struktur der Verlustfunktion zu ändern. Eine der einfachen Änderungen, die von Xudong Mao et al., 2016, vorgeschlagen wurden , ist das Ersetzen der Verlustfunktion $$$\ mathcal {L} _ \ text {GAN}$für ein paar einfache Funktionen $$$V_ \ text {LSGAN}$, die auf Quadraten kleinerer Fläche basieren. Dies führt zu einer Stabilisierung des Trainingsprozesses, wodurch bessere Bilder und eine geringere Kollapswahrscheinlichkeit bei ungedämpften Verläufen erzielt werden.

Ein weiteres Problem, auf das Forscher gestoßen sind, ist die Schwierigkeit, hochauflösende Bilder zu erhalten, teilweise weil ein detaillierteres Bild dem Diskriminator mehr Informationen gibt, um gefälschte Bilder zu erkennen. Moderne GANs beginnen, das Netzwerk mit Bildern mit niedriger Auflösung zu trainieren und fügen nach und nach immer mehr Ebenen hinzu, bis die gewünschte Bildgröße erreicht ist.


Das schrittweise Hinzufügen von Ebenen mit höherer Auflösung während des GAN-Trainings erhöht die Stabilität des gesamten Prozesses sowie die Geschwindigkeit und Qualität des resultierenden Bildes erheblich.

Bild-zu-Bild-Übertragung

Bisher haben wir darüber gesprochen, wie Bilder aus zufälligen Sätzen von Eingabedaten generiert werden können. SPADE verwendet jedoch nicht nur zufällige Daten. Dieses Netzwerk verwendet ein Bild, das als Segmentierungskarte bezeichnet wird: Es weist jedem Pixel eine Materialklasse zu (z. B. Gras, Holz, Wasser, Stein, Himmel). Aus diesem Bild ist die Karte SPADE und erzeugt etwas, das wie ein Foto aussieht. Dies wird als "Bild-zu-Bild-Übertragung" bezeichnet.


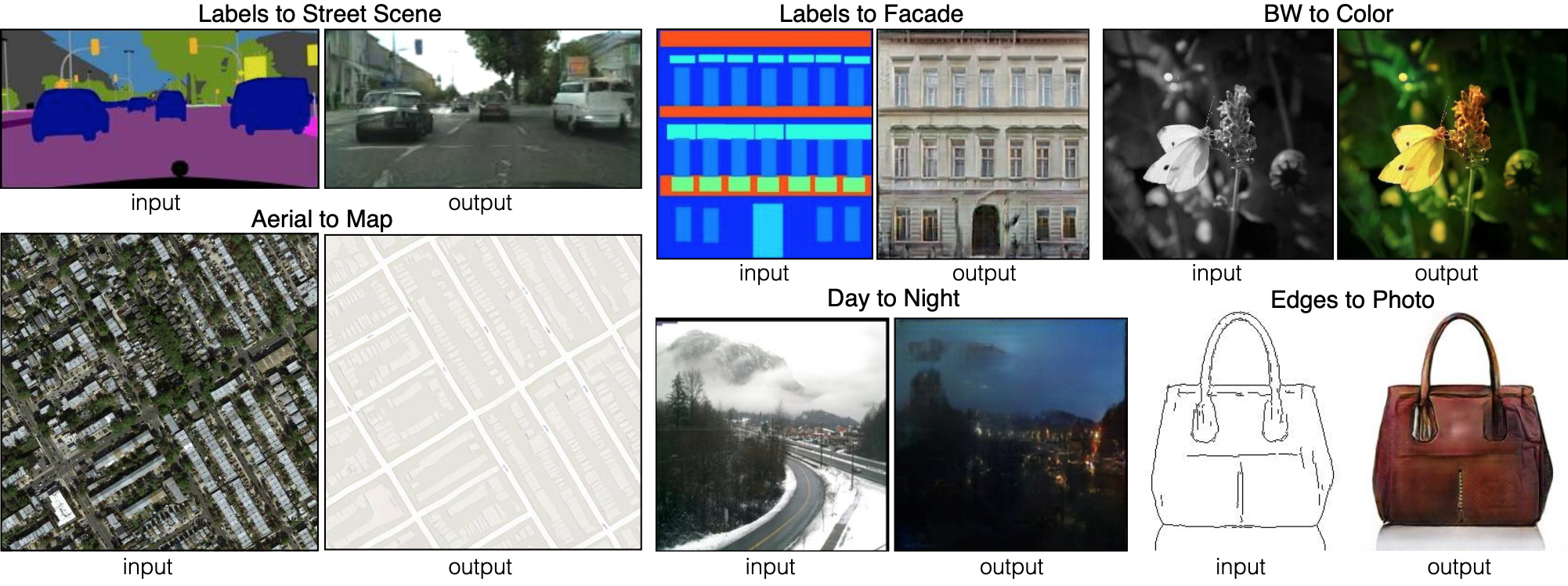Sechs verschiedene Arten von Bild-zu-Bild-Sendungen, die von pix2pix demonstriert werden. Pix2pix ist der Vorgänger der beiden Netzwerke, auf die wir weiter eingehen werden: pix2pixHD und SPADE.

Damit der Generator diesen Ansatz lernen kann, benötigt er einen Satz Segmentierungskarten und entsprechende Fotos. Wir modifizieren die GAN-Architektur so, dass sowohl der Generator als auch der Diskriminator eine Segmentierungskarte erhalten. Der Generator benötigt natürlich eine Karte, um zu wissen, "wie gezeichnet werden soll". Der Diskriminator benötigt es auch, um sicherzustellen, dass der Generator die richtigen Dinge an den richtigen Stellen platziert.

Während des Trainings lernt der Generator, kein Gras dort zu platzieren, wo auf der Segmentierungskarte „Himmel“ angezeigt wird, da der Diskriminator sonst leicht ein falsches Bild erkennen kann und so weiter.


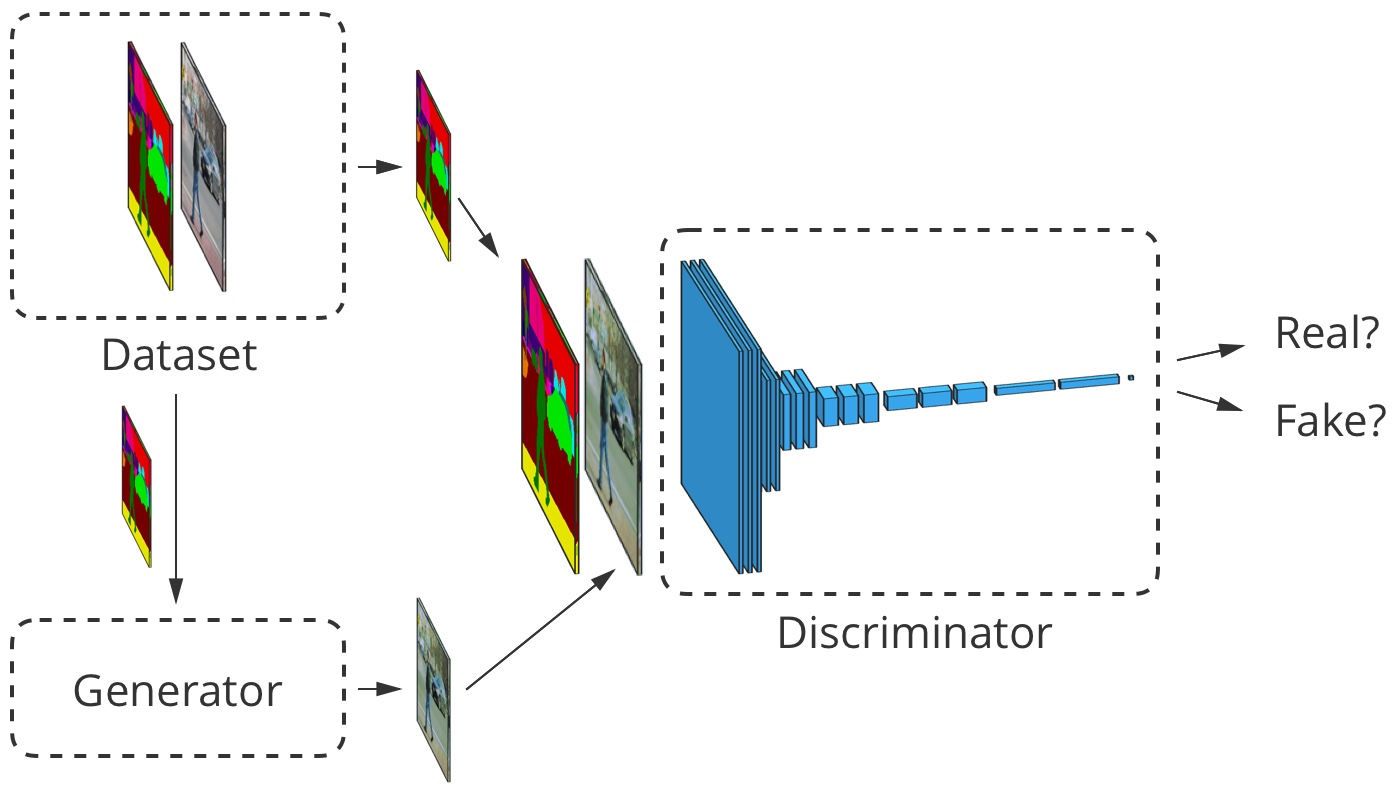Für die Bild-zu-Bild-Übersetzung wird das Eingabebild sowohl vom Generator als auch vom Diskriminator akzeptiert. Der Diskriminator empfängt zusätzlich entweder die Generatorausgabe oder die wahre Ausgabe aus dem Trainingsdatensatz. Beispiel

Entwicklung von Bild-zu-Bild-Übersetzern

Schauen wir uns einen echten Bild-zu-Bild-Übersetzer an: pix2pixHD . SPADE ist übrigens größtenteils auf das Bild und die Ähnlichkeit von pix2pixHD ausgelegt.

Für einen Bild-zu-Bild-Übersetzer erstellt unser Generator ein Bild und akzeptiert es als Eingabe. Wir könnten nur eine Faltungsschichtkarte verwenden, aber da Faltungsschichten Werte nur in kleinen Bereichen kombinieren, benötigen wir zu viele Schichten, um hochauflösende Bildinformationen zu übertragen.

pix2pixHD löst dieses Problem effizienter mit Hilfe des "Encoders", der die Skalierung des Eingabebildes verringert, gefolgt vom "Decoder", der die Skalierung erhöht, um das Ausgabebild zu erhalten. Wie wir gleich sehen werden, hat SPADE eine elegantere Lösung, für die kein Encoder erforderlich ist.


Pix2pixHD-Netzwerkdiagramm auf "hohem" Niveau. Die "Rest" -Blöcke und "+ Operation" beziehen sich auf die "Skip Connections" -Technologie aus dem Residual Neural Network . Es gibt Sprungblöcke im Netzwerk, die im Codierer und Decodierer miteinander verbunden sind.

Die Chargennormalisierung ist ein Problem

Fast alle modernen neuronalen Faltungsnetzwerke verwenden die Chargennormalisierung oder eines ihrer Analoga, um den Trainingsprozess zu beschleunigen und zu stabilisieren. Die Aktivierung jedes Kanals verschiebt den Mittelwert auf 0 und die Standardabweichung auf 1 vor einem Paar von Kanalparametern $$$\ beta$und $$$\ gamma$lass sie wieder denormalisieren.

$$$y = \ frac {x - \ mathrm {E} [x]} {\ sqrt {\ mathrm {Var} [x] + \ epsilon}} * \ gamma + \ beta$

Leider schadet die Batch-Normalisierung den Generatoren, was es dem Netzwerk erschwert, einige Arten der Bildverarbeitung zu implementieren. Anstatt einen Stapel von Bildern zu normalisieren, verwendet pix2pixHD einen Normalisierungsstandard , der jedes Bild einzeln normalisiert.

Pix2pixHD Training

Moderne GANs wie pix2pixHD und SPADE messen den Realismus ihrer Ausgabebilder etwas anders als für das ursprüngliche Design generativer Konkurrenznetzwerke beschrieben.

Um das Problem der Erzeugung hochauflösender Bilder zu lösen, verwendet pix2pixHD drei Diskriminatoren derselben Struktur, von denen jeder das Ausgabebild in einem anderen Maßstab empfängt (normale Größe, um das Zweifache reduziert und um das Vierfache reduziert).

Pix2pixHD verwendet $$$V_ \ text {LSGAN}$und enthält auch ein weiteres Element, das die Schlussfolgerungen des Generators realistischer machen soll (unabhängig davon, ob dies dazu beiträgt, den Diskriminator zu täuschen). Dieser Artikel $$$\ mathcal {L} _ \ text {FM}$Dies wird als "Feature Matching" bezeichnet und ermutigt den Generator, die Verteilung der Schichten gleich zu gestalten, wenn eine Unterscheidung zwischen realen Daten und den Ausgaben des Generators simuliert wird, wodurch die Minimierung minimiert wird $L_1 Entfernung$zwischen ihnen.

Die Optimierung läuft also auf Folgendes hinaus:

$$$$ Anzeige $$ \ begin {Gleichung *} \ min_G \ bigg (\ lambda \ sum_ {k = 1,2,3} V_ \ text {LSGAN} (G, D_k) + \ big (\ max_ {D_1, D_2 , D_3} \ sum_ {k = 1,2,3} \ mathcal {L} _ \ text {FM} (G, D_k) \ big) \ bigg) \ end {Gleichung *}, $$ display $$

wobei Verluste durch drei Unterscheidungsfaktoren und Koeffizienten summiert werden $$$\ lambda = 10$, die die Priorität beider Elemente steuert.


pix2pixHD verwendet eine Segmentierungskarte, die aus einem echten Schlafzimmer besteht (in jedem Beispiel links), um ein falsches Schlafzimmer (rechts) zu erstellen.

Obwohl Diskriminatoren den Bildmaßstab reduzieren, bis sie das gesamte Bild zerlegen, halten sie an „Punkten“ der Größe 70 × 70 (in geeigneten Maßstäben) an. Dann fassen sie einfach alle Werte dieser „Punkte“ für das gesamte Bild zusammen.

Und dieser Ansatz funktioniert gut, da die Funktion $$$\ mathcal {L} _ \ text {FM}$, , $$$V_\text{LSGAN}$. , .


pix2pixHD . CelebA , .

pix2pixHD?

, . , pix2pixHD .

, pix2pixHD , , , . , . «» () $$$0$. β- , : , «», «», «» - .


pix2pixHD . , , .

— SPADE.

: SPADE

- : - () (SPADE).

SPADE , , γ, β, , . , 2 .


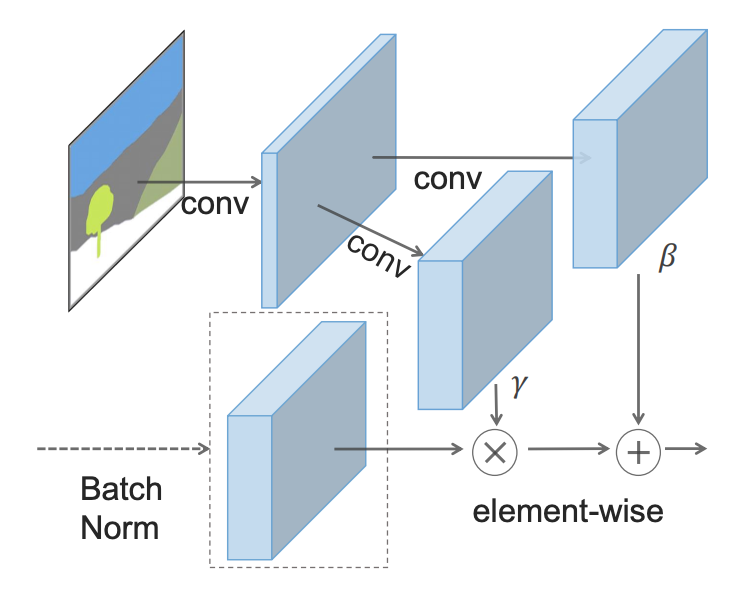, SPADE .

SPADE « », ( ):


SPADE pix2pixHD

, «» , . GAN, . (« »). «» pix2pixHD, .

SPADE , pix2pixHD, : $$$V_\text{LSGAN}$hinge loss .

:


SPADE pix2pixHD

, SPADE . . GauGAN «» , . , - SPADE , «» , .

, SPADE , «» .



, , «». SPADE , , ? 55, «».

, , 5x5 . , .

SPADE , , , , pix2pixHD. , .

SPADE — (, , , ).


SPADE , .

: , $$$Z$, . , , SPADE , , .

, . , , .

So funktioniert SPADE / GaiGAN. Ich hoffe, dieser Artikel hat Ihre Neugier auf die Funktionsweise des neuen NVIDIA-Systems befriedigt. Sie können mich über Twitter @AdamDanielKin oder per E-Mail an adam@AdamDKing.com kontaktieren.