Bei autoregressiver Schätzung der spektralen Dichte eines stationären Signals

Methoden zur spektralen Schätzung stationärer Zufallsprozesse auf der Basis der schnellen Fourier-Transformation (FFT) sind bekannt und in der Ingenieurpraxis weit verbreitet. Zu ihren Nachteilen gehört insbesondere eine hohe Streuung (geringe Genauigkeit) der Schätzung mit einem unzureichend langen Beobachtungsintervall für den Prozess, die sich visuell normalerweise in einem starken "eingerückten" Diagramm der Leistungsspektraldichte (PSD) manifestiert. Eine der alternativen Methoden zur Spektralschätzung ist die autoregressive Methode, die im folgenden Beispiel betrachtet wird und in der technischen Praxis viel weniger bekannt ist. In vielen Fällen macht es die Methode relativ einfach, eine viel bessere Schätzung der PSD (Abb. 1) und manchmal sogar noch tiefere Informationen über den untersuchten Zufallsprozess zu erhalten.


Abb. 1 Klassische und autoregressive Bewertung der PSD des „kurzen“ Prozesses

Zu Demonstrationszwecken wurde ein zeitdiskretes Signal (Sequenz) x [i] synthetisiert. Das Signal wird unter Verwendung eines ARMA-Modells (digitales Filter) modelliert, das die Eigenschaften eines mechanischen Systems (1) simuliert - Verschieben des Materialpunkts x (t) in einem Oszillator mit einer Masse mit den Parametern m = 1 kg, c = 100 N / m, k = 2, 5 kg / s und durch eine Kraftstörung - Gaußsches "weißes" (unter Berücksichtigung der Diskretisierung) Rauschen f (t) mit einer Dispersion von 1 N ² , das Abtastintervall in der Zeit Δt = 0,12 s.



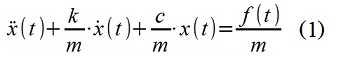
Modell gebaut (2). Die Methode zur Erstellung des Modells wurde hier bereits früher berücksichtigt.

x [i] - 0,6388 · x [i-1] + 0,7408 · x [i-2] = 0,009667 · f [i-1] (2)

Unter Verwendung von (2) wurde eine Sequenz von 50.000 Proben synthetisiert, für die ein Generator einer normalverteilten Zufallsvariablen randn () einer bekannten Softwareumgebung verwendet wurde.

Nach Abschluss der Simulation des Prozesses x [i] werden die quantitativen Parameter des Modells (2) als unbekannt angenommen - nur der Prozess selbst und zum Teil allgemeinere Informationen über die Eigenschaften des Modells stehen für die Forschung zur Verfügung.

Eine spektrale Schätzung der 50.000-Punkte-Sequenz wurde unter Verwendung der Welch-Methode durchgeführt, die Segmentgröße wurde gleich 256 Proben genommen, das Hamming-Fenster und eine 60% ige Überlappung der Segmente wurden angewendet. Die Standardabweichung einer solchen Schätzung, basierend auf der Tatsache, dass die Sequenz eine Länge von ungefähr 200 nicht überlappenden Segmenten hat, kann grob auf ~ 7% geschätzt werden.

Unter der Annahme, dass unter realen Bedingungen im Experiment eine viel kürzere Sequenz für die Forschung verfügbar ist, wurden Studien nur an den ersten 500 Proben dieses Signals durchgeführt.

Eine Schätzung wird nach der Welch-Methode mit denselben Parametern erhalten. Die Standardabweichung einer solchen Schätzung beträgt ~ 70%, wobei eine sehr starke „Rauheit“ des Diagramms erkennbar ist (Abb. 2).


Abb.2. Bewertung der PSD der "langen" und "kurzen" Prozesse nach der klassischen Methode

Basierend auf der Tatsache, dass wir die ungefähre Form der Funktion (Grafik) des SPM-Prozesses kennen (zum Beispiel basierend auf der bekannten physikalischen Natur des Prozesses - einem Einzelmassenoszillator unter weißem Rauschen oder aus der Bewertung ähnlicher Prozesse, für die längere Implementierungen verfügbar sind), haben wir uns für eine Bewertung mit entschieden unter Verwendung des autoregressiven Modells zweiter Ordnung (AR (2) oder = ARMA (2.0)).

Die Bestimmung der Reihenfolge des Modells ist ein sehr wichtiger Punkt, ein Fehler in der Reihenfolge kann zu sehr groben Fehlern in den Schätzergebnissen führen. Es gibt Methoden, die hier noch nicht berücksichtigt wurden, um die Reihenfolge des Modells nur anhand des zu analysierenden Prozesses zu bestimmen.

Die Schätzung der Modellparameter wurde unter Verwendung der bekannten Yule-Walker-Gleichungen für den autoregressiven Prozess durchgeführt (leicht modifiziert, um die Struktur des Skripts leicht zu vereinfachen):



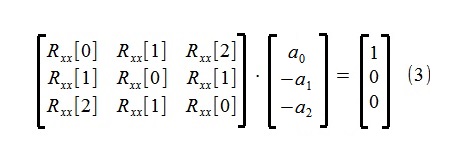
Wie aus den Gleichungen ersichtlich ist, werden zur Bestimmung der Parameter nur die ersten drei Mitglieder der autoregressiven Sequenz Rxx [0], Rxx [1], Rxx [2] verwendet, die aus der anfänglichen 500-Punkte-Sequenz x [i] durch das Korrelogrammverfahren geschätzt wurden ~ 4,5%.

(Übrigens ist es klar, dass die „Nachteile“ vor einer ₁ , a2 ₂ usw. äußerst unpraktisch sind. Sie erschienen aufgrund der überwiegend „prädiktiven“ Verwendung von ARMA-Modellen in der Wirtschaft in ihren früheren „technischen“ Quellen Nein. Ich bezweifle bereits, dass es notwendig war, hier ein solches Verständnis der AR-Koeffizienten anzuwenden.)

Die Korrelationsmatrix in (3) hat in der Praxis immer eine strikte diagonale Prävalenz Rxx [0] | > | Rxx [i] |, auch aufgrund von Beobachtungsgeräuschen, aufgrund derer es keine Schwierigkeiten bei der Handhabung gibt (Suche nach einer Lösung (3)).

(Um die Frage nach der Größe des statistischen Simulationsfehlers zu klären, ist es interessant, beispielsweise die Schätzung Rxx [0] = 2,2606e-04 m ² aus 500 Proben im Vergleich zur erhaltenen Korrelogrammschätzung der Varianz aus 50.000 Proben = 2,4238e-04 m ^{2 zu} erwähnen und die Schätzung der PSD-Fläche durch den Integranden nach der Welch-Methode für 50.000 Proben (Abb. 2) = 2,4232e-04 m ² )

Nach dem Ersetzen der gefundenen Schätzungen Rxx [i] haben wir:



Die folgenden Modellparameter werden mit ₀ = 11325,9 bestimmt; a ₁ = 7090,1; a ₂ = -8411,5; Wie aus (3) ersichtlich ist, wurde hier die Streuung des hypothetischen ankommenden weißen Rauschens auf 1 gesetzt, wobei stattdessen die Verstärkung a _{0 bestimmt wurde} . Eine autoregressive Schätzung der PSD wird durch die Fourier-Transformation über eine Folge von Koeffizienten a ₀ , a ₁ , a ₂ konstruiert:




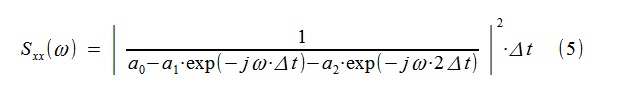
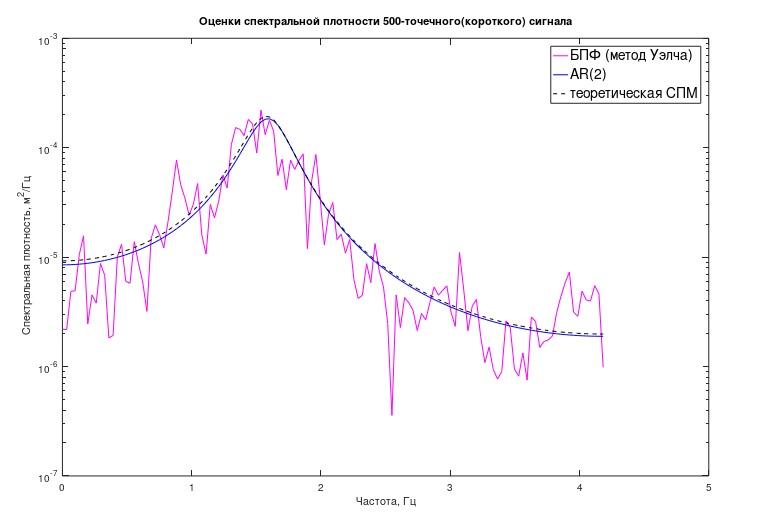Abb. 3 Klassische und autoregressive Bewertung der PSD des „kurzen“ Prozesses

Auf die gleiche Weise wurde gemäß einem Ausdruck ähnlich (5) der "theoretische" Zeitplan der PSD früher konstruiert, nur die Modellkoeffizienten dort wurden natürlich anders genommen (von (2)).
Aus der Grafik ist ersichtlich, dass sich die AR-Schätzung der PSD als sehr nahe an der theoretisch erwarteten herausstellte. Zusätzlich zum Diagramm kann versucht werden, einige analytische Eigenschaften des Prozesses und des zugehörigen mechanischen Systems zu bewerten. In diesem Fall sind dies die "Pole" des Modells, die die Frequenzen der "resonanten" Peaks des Modells und die zugehörigen "Qualitätsfaktoren" numerisch charakterisieren.

Aus (5) finden wir die Beziehung zum Suchen der Diskontinuitäten der Übertragungsfunktion unseres Modells unter Verwendung der Laplace-Transformation (Ersetzen von jω durch λ = -ε + jω):



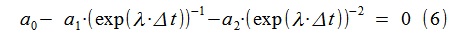
Für das erhaltene AR-Modell wurde auf diese Weise λ _1,2 = -1,5427 ± j · 10,1514 berechnet, was dem ursprünglichen Modell, das zur Erzeugung des Prozesses verwendet wurde, sehr nahe kommt
λ _1,2theor = -1,2500 ± j · 9,9216 (d. h. die Positionen der Resonanzspitze 1,615 Hz (theoretisch) bzw. 1,579 Hz (bestimmt)).


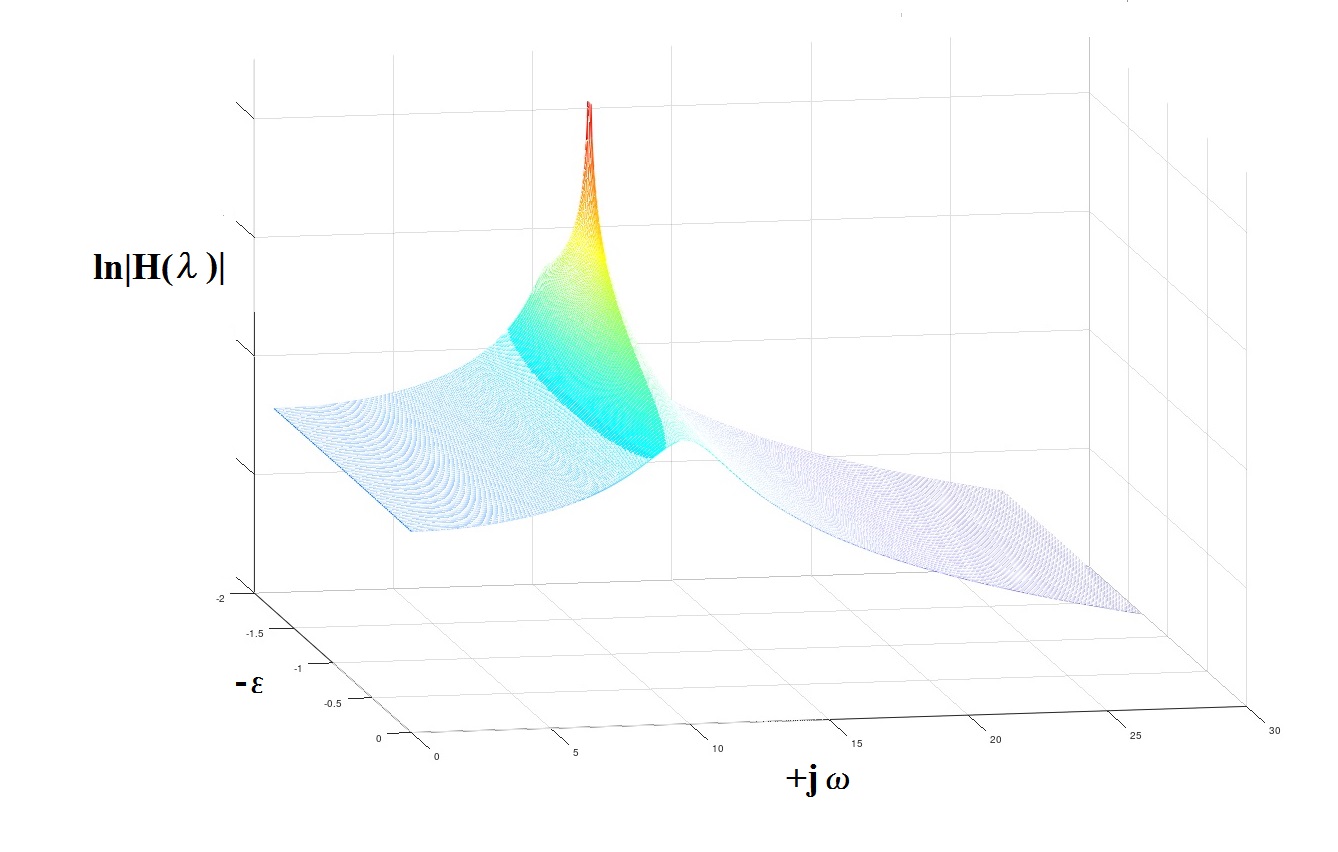Abb. 4 Über das Konzept der "Pole"

Ein paar Kommentare und Empfehlungen zum Abschluss.

1. Die „übermäßige“ (zu große) Ordnung des AR-Modells ist im Hinblick auf das Risiko, eine PSD-Schätzung mit groben Fehlern zu erhalten, normalerweise viel weniger gefährlich als unzureichend.
2. In der Regel ermöglicht die AR-Modellierung eine ziemlich genaue Bestimmung der Resonanzfrequenzen jω _k und eine viel weniger genaue Bestimmung der Breiten der entsprechenden "Peaks" -ε _k
3. ARMA - Das Modell kann sich als viel kleiner herausstellen (Größe) als das AR-Modell, das laut vielen Quellen darauf abzielen soll, die Genauigkeit des Modells zu verbessern. Die Bewertung des MA-Teils des Modells ist jedoch viel schwieriger und kann im Allgemeinen den ersten Schritt zum Erhalten eines AR-Modells großer Ordnung umfassen, um es weiter in den MA-Teil umzuwandeln. Im Zusammenhang mit diesen Quellen wird auch eine alternative Meinung darüber geäußert, ob es ratsam ist, genau AR-Modelle für die Spektralschätzung zu verwenden, wenn auch von höherer Ordnung.
4. Für sehr kurze sowie für instationäre Prozesse wird in (3) üblicherweise anstelle der Schätzmatrix der Autokorrelationsfunktion die Kovarianzmatrix verwendet.
5. Für eine detaillierte Untersuchung des Problems der autoregressiven Spektralschätzung hat S.L. Marple ml. "Digitale Spektralanalyse und ihre Anwendungen", M., Mir, 1990