Über die Nähe der Gipfel

„Bevor du das verstehst, scheint es ein Wunder zu sein. Aber danach gibt es nichts Besonderes mehr. “

Nein, nicht über Berge, - über Zählungen. In der Mathematik gibt es Fragen, deren Formulierung jedem zugänglich ist, aber die Lösung ist nicht trivial und ohne besondere Vorbereitung schwer zu erklären. Eines dieser Probleme kann kurz wie folgt ausgedrückt werden: Wie werden Entfernungen in gerichteten Graphen korrekt berechnet? Dieses etwas abstrakte Problem kann auf eine ganz bestimmte Motivationsaufgabe reduziert werden. Es passt in ein Bild:

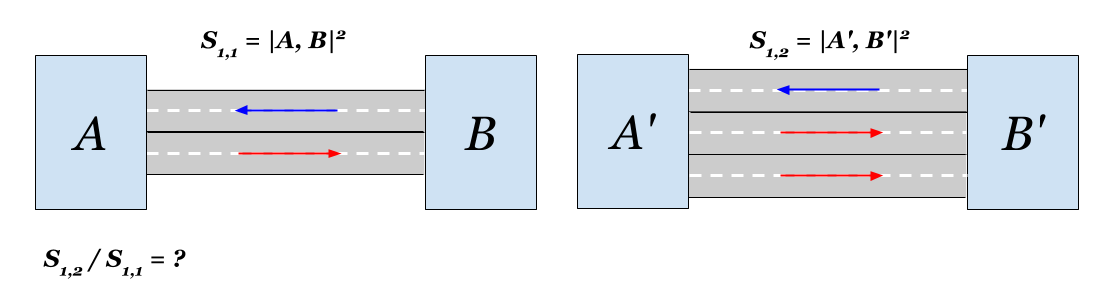
1. Erklärung des Problems. Ich lebe von einem, aber du von dem anderen.

Eine kleine Stadt ist (zum Beispiel durch einen Fluss, obwohl im Zusammenhang mit den Gipfeln die Schlucht besser geeignet ist) in zwei Bezirke (Teile) unterteilt. $$$A$ und $$$B$ . Die Kommunikation zwischen den Bezirken erfolgt über eine einzige Straße (Brücke), die zweispurig ist: seitlich von $$$A$ zu $$$B$ und umgekehrt. Im Zusammenhang mit dem Bevölkerungswachstum stellte sich die Frage nach der Erhöhung der Straßenkapazität. Geld ist wie immer kaum genug und nur genug für eine Spur in eine Richtung. Es ist klar, dass auch nur eine Spur Regionen näher zusammenbringen wird, aber die Frage ist, wie viel genau? Sie sind ein urbaner verrückter Mathematiker, und Sie wurden eingeladen, um eine vernünftige Antwort zu erhalten.

Wie viel näher sind die Bereiche, wenn Sie einen weiteren Streifen in eine Richtung bauen?

Formulierung für Fortgeschrittene

Anstelle von Königsbergbrücken kann eine etwas strengere graphentheoretische Sprache verwendet werden. Es gibt also einen gerichteten Graphen mit zwei Eckpunkten (Knoten). $$$A$ und $$$B$ . Die Größe der Verbindung (Leitfähigkeit, Bandbreite) in Vorwärts- und Rückwärtsrichtung ist anfangs gleich. Die Frage ist, um wie viel sich der Abstand zwischen den Knoten ändert, wenn die Leitfähigkeit in einer der Richtungen verdoppelt wird.

Und ja, wenn Sie ein echter Schweißer für Mathematiker sind, können Sie eine Lösung für alle direkten Werte und Rückmeldungswerte anbieten (und begründen). Ideal für ein Diagramm mit einer beliebigen Anzahl von Knoten und Verknüpfungen.

Intimität und betrunkene Wanderungen

Es ist klar, dass der übliche (Kilometer-) Abstand zwischen Regionen nicht vom Vorhandensein oder Fehlen der Straße abhängt. Deshalb passt es hier nicht - wir müssen uns auf Kommunikation verlassen. Je mehr Bezirke miteinander verbunden sind - je näher sie sind - desto mehr Einwohner können pro Zeiteinheit in ein anderes Gebiet gelangen.

Um das Maß der Nähe zwischen Knoten eines ungerichteten Graphen zu bestimmen, kann der sogenannte Widerstandsabstand verwendet werden. Zuvor haben wir die Eigenschaften dieses Abstands auf dem Habr bereits in mehreren Artikeln beschrieben .

Der Widerstandsabstand entspricht dem Konzept des effektiven Widerstands, wenn es um das elektrische Netz geht. Daher kann das Problem in der elektrischen Sprache wie folgt formuliert werden. Zwischen zwei Knoten sind zwei Dioden gleicher Leitfähigkeit gegen den Uhrzeigersinn geschaltet. Wie ändert sich der Widerstand zwischen diesen Punkten, wenn Sie eine weitere Diode hinzufügen? (Ich entschuldige mich, wenn die elektrische Sprache versagt hat und ich hier Unsinn geschrieben habe).

Effektiver Widerstand kann auch in der Markov-Sprache für die Wahrscheinlichkeiten betrunkener zufälliger Spaziergänge interpretiert werden (für diejenigen, die sich mit dem Thema befassen möchten - Google „Zufällige Spaziergänge und elektrische Netzwerke“).

Der Widerstandsabstand ist quadratisch, - entspricht dem Quadrat des linearen Abstands. Quadratische Abstände werden auch Quadrans genannt . Da bei diesem Problem jedoch keine anderen (linearen) Abstände verwendet werden, benötigen wir hier nicht den Begriff Quadrans. (Auch ohne gibt es genug Vogelzunge)

Im Allgemeinen sieht der Begriff "Widerstandsabstand" auch nicht gut aus. Er impliziert, dass es sich um eine ungewöhnliche Distanz handelt, die der Wissenschaft unbekannt ist. Tatsächlich ist der Widerstandsabstand der übliche euklidische Abstand . Aber im affinen Raum. Wir nutzen diese Funktion weiter.

Und was ist eigentlich das Problem?

Wenn wir wissen, was ein "Widerstandsabstand" ist, warum können wir ihn dann nicht für einen bestimmten Graphen "einfach nehmen und berechnen"?

Hm. Im Prinzip einfach. Wenn es sich um ein ungerichtetes Diagramm handelt. Wenn die Stadt Streifen in beide Richtungen gebaut hätte, hätte sich der Widerstandsabstand um genau die Hälfte verringert. Da der Widerstand umgekehrt proportional zur Leitfähigkeit ist, hat sich die Leitfähigkeit (Durchsatz) verdoppelt. Und wenn ich zwei Bänder in jede Richtung hinzufügen würde, würde sich der Abstand um das Dreifache verringern. Hier ist alles ziemlich trivial. (Und wahrscheinlich kann hier jemand bereits die allgemeine Form der Lösung erraten. Und wir gehen weiter).

Wenn die gegensätzlichen Beziehungen nicht gleich sind, wird alles kompliziert. Und ziemlich streng.

Es gibt keinen einfachen, allgemein anerkannten Weg, um die Nähe von Spitzen (Widerstandsabständen) in einem Richtungsgraphen zu bestimmen.

(Dies ist meine These - vielleicht kann mich jemand überzeugen). "Nein" - hier bedeutet, dass es nicht in den Lehrbüchern, im Wiki und in den Köpfen steht (genauer gesagt - es gibt viele verschiedene Wege von verschiedenen Autoren, die unterschiedliche Annahmen und Definitionen erfordern). Es gibt einen Weg (wenn auch nicht so einfach). In diesem Artikel beschreiben wir es nur.

Die Bestimmung des Abstands bei gerichteten Verbindungen erfordert eine Klärung, wenn es sich um einen gerichteten Graphen handelt (nicht kommutative Metrik, ich entschuldige mich). Sie können über die Entfernung von sprechen $$$A$ vorher $$$B$ , aber du kannst aus $$$B$ vorher $$$A$ . Und höchstwahrscheinlich sind diese Abstände nicht immer gleich. Über welche Entfernungen sprechen wir im Problem?

Euklidische Distanzregeln

Wir werden auftauchen und tief durchatmen. Wir haben bereits erwähnt, dass der Widerstandsabstand der übliche euklidische ist. Dies bedeutet, dass seine Definition auf die Definition des euklidischen Abstands als Norm der Differenz zweier Elemente reduziert werden kann:

$$$S (A, B) = | A - B | ^ 2 = (A - B) ^ 2 = (A - B) \ cdot (A - B) = S (B, A) \ quad (1)$

Diese Definition hängt nicht von der Reihenfolge der Elemente ab - dies ist der kommutative Abstand, die Nähe (genauer gesagt der Abstand) der Elemente. Ein Punkt in einem Ausdruck bedeutet eine skalare Produktoperation (metrischer Raum). Dementsprechend kann Ausdruck (1) offenbart werden:

$$$S (A, B) = S (B, A) = A ^ 2 + B ^ 2 - A \ cdot B - B \ cdot A \ quad (2)$

Hier $$$A ^ 2 = A \ cdot A$ , $$$B ^ 2 = B \ cdot B$ - Normen der Elemente. Wenn es um Diagramme geht, sind die Normen der Elemente normalerweise Null. Im ursprünglichen Problem wird nichts über die Normen gesagt, so dass Sie sie auf Null setzen können (mehr darüber, was die Normen der Elemente im affinen Raum bedeuten. Hier und noch mehr Details hier ). Dann hat der Ausdruck für die gewünschte Entfernung die Form:

$$$S (A, B) = - (A \ cdot B + B \ cdot A) = s_ {AB} + s_ {BA} \ quad (3)$

Gemäß Ausdruck (3) müssen zur Lösung des Problems lediglich die Skalarprodukte von Elementen (Knoten) in einem gerichteten Diagramm gefunden werden (es ist leicht zu sagen, aber wie geht das?).

Auf dem Weg zeigt Formel (3), dass unser allgemeines (kommutatives) Maß für die Nähe zwischen Elementen $$$A$ und $$$B$ ist die Summe zweier gerichteter Entfernungen:

$$$s_ {AB} = - A \ cdot B$ - Richtungsabstand von $$$A$ vorher $$$B$ ,
$$$s_ {BA} = - B \ cdot A$ - Richtungsabstand von $$$B$ vorher $$$A$ .

2. Die Entscheidung. Langer Weg in den Dünen

Das Grollen ließ nach. Der Spaß ist vorbei. Dann kommen die langweiligen Details der Beschreibung des Wesens der Methode zur Berechnung des Skalarprodukts zwischen Knoten eines gerichteten Graphen. Dies ist der Teil, den ich nicht "auf einfache Weise an den Fingern" sagen kann. Aber hier ist das Wichtigste im Artikel. Etwas, das es wert ist, Zeit damit zu verschwenden.

Die allgemeine Argumentation lautet wie folgt. Wir übertragen sorgfältig und ohne Emotionen neuer zusätzlicher Annahmen die bekannten Eigenschaften der Metrik symmetrischer Räume auf asymmetrische. Alles, was benötigt wird, ist die Berücksichtigung der Besonderheiten der Metrik in affinen Räumen.

Jeder verbundene Graph (ob gerichtet oder nicht) definiert einen affinen metrischen Raum. Einige Eigenschaften solcher Räume bei der symmetrischen (kommutativen) Ausführung wurden (chaotisch) in der bereits erwähnten Artikelserie oder genauer und detaillierter im erwähnten Longrid beschrieben . Beeilen Sie sich nicht, um zu wechseln - unten geben wir (allerdings durch den Zungenbrecher) die Hauptdrücke.

Affiner metrischer Raum (ungerichteter Graph)

Was ist wichtig? Zuerst bekannt.

1. Die Affinität des Raumes bedeutet, dass die Konzepte von Vektor und Element im Raum unterschiedlich sind. Vektor ist der Unterschied der Elemente. Dieses scheinbar unbedeutende Merkmal führt zu erheblichen Konsequenzen, wenn eine Metrik im Raum definiert wird.

2. Der Raum wird durch eine Basis definiert, die aus Elementen besteht. Die Eckpunkte des Graphen bilden die Basis des Raums. Beziehungen in einem Diagramm bestimmen seine metrischen Eigenschaften.

3. Eine Graph-Konnektivitätscharakteristik ist die Adjazenzmatrix . Für metrische (und andere) Eigenschaften ist jedoch der Laplace- Wert des Graphen (Kirchhoff-Matrix) wichtiger $$$L$ .

4. Der Laplace-Wert eines Graphen ist ein fast metrischer Tensor. "Fast" - hier bedeutet, dass es unvollständig ist. Laplace ist eine entartete Matrix und daher nicht invertierbar. Und der standardmäßige metrische Tensor ist vollständig reversibel.

Jetzt weniger bekannt.

5. Der Unterschied zwischen Elementen und Vektoren in einem metrischen affinen Raum führt zur Existenz eines Nullvektors darin $$$\ mathbb z$ . Das Skalarprodukt von Elementen mit einem Nullvektor in einem kommutativen (symmetrischen) Raum ist gleich Eins (in einem nicht kommutativen Raum hängt es von der Multiplikationsrichtung ab). Ohne einen Nullvektor ist der Graphraum nicht vollständig! Es ist wichtig.

6. Das orthogonale Zentrum der Basis ist in Bezug auf den Nullvektor dual. $$$Z$ . Dies ist ein solches Element, das orthogonal zu allen anderen Elementen der Basis ist (mit Ausnahme des Nullvektors). Denken Sie daran, dass die Orthogonalität von Elementen bedeutet, dass ihr Skalarprodukt Null ist. Das Orthozentrum eines Dreiecks ist der umschriebene Kreis . Ja, in einem vollständigen affinen Raum ist ein Element mit einer Norm ungleich Null kein Punkt, sondern eine n-dimensionale Kugel.

7. Der Laplace-Wert des Graphen wird zusammen mit den Koordinaten des orthogonalen Zentrums vollständig (ein vollwertiger metrischer Tensor). Mit anderen Worten, voller Laplace $$$Lm$ Ist ein gewöhnlicher Graf Laplace $$$L$ aber begrenzt durch die Schwerpunktkoordinaten des orthogonalen Zentrums.

8. Die Umkehrung des vollständigen Laplace ermöglicht es, einen vollständigen Gramian zu erhalten $$$Gm$ - die Matrix der Skalarprodukte der Elemente der Basis (in unserem Fall die Eckpunkte des Graphen). Dieses Gramm ist auch ein vollwertiger metrischer Raumtensor.

9. Die Rahmung eines vollständigen Grammian ist ein Tupel von Einheiten (Skalarprodukte von Basiselementen und ein Nullvektor). In der Ecke - Null ist dies die Norm des Nullvektors selbst.
Die berühmte Cayley-Menger- Matrix ist ein fast normaler Gramian.

Als Ergebnis schließen wir, dass gemäß Anspruch 8 das Problem der Bestimmung von Skalarprodukten (und daher Abständen) zwischen den Knoten des Graphen auf die Bestimmung des anfänglichen metrischen Tensors der Basis reduziert wird $$$Gm$ .

Wir brauchen eine Methode zur Erstellung eines vollständigen Grammatikgraphen $$$Gm$ für einen gegebenen (unvollständigen) Laplace $$$L$ .

Bei symmetrischen Bindungen verursacht die Konstruktion eines vollständigen Gramian aus dem Laplace (und umgekehrt) keine besonderen Schwierigkeiten. In diesem Fall sind die Skalarprodukte der Elemente der Basis und des Nullvektors kommutativ - sie hängen nicht von der Reihenfolge der Multiplikation ab:

$$$\ mathbb z \ cdot A = A \ cdot \ mathbb z = 1$

Für gerichtete Graphen (nicht kommutative Räume) ist das Problem kompliziert. Schon allein deshalb, weil sich die Anzahl der möglichen Verbindungen im gerichteten Graphen verdoppelt.

Nicht kommutativer affiner Raum (gerichteter Graph)

Über die Eigenschaften des Laplace des gerichteten Graphen haben wir auch bereits über den Habr geschrieben . Sie erklärten, wie man die Potenziale des Laplace nutzt, um Objekte zu ordnen. In Bezug auf die Basen sind die Potentiale des Laplace die Doppelkoordinaten des Nullvektors (Vernichter des Laplace).

In diesem Artikel interessieren uns metrische Eigenschaften. Wenn der Graph gerichtet ist, hängt das Skalarprodukt zwischen seinen Eckpunkten von der Reihenfolge ab:

$$$A \ cdot B \ ne B \ cdot A$

Dies bedeutet, dass die Doppelkoordinaten in den gerichteten Graphen aufgeteilt werden (in links und rechts). Die Werte der Skalarprodukte des Nullvektors und der Elemente der Basis (angrenzend an das Gramm) hängen auch von der Reihenfolge der Faktoren ab. Und deshalb ist hier im Gegensatz zum kommutativen Raum eine Hälfte der Doppelkoordinaten des Nullvektors unbekannt und muss bestimmt werden.

$$$\ mathbb z \ cdot A \ ne A \ cdot \ mathbb z$

Es sind jedoch viele Mengen bekannt.

Erstens ist der Laplace selbst bekannt. Darüber hinaus ist bekannt, dass die Summe seiner Zeilen Null ist (im allgemeinen Fall ist dies eine optionale Anforderung, bei Laplace-Richtern mit gerichteten Graphen ist dies jedoch normalerweise der Fall). Es ist auch wichtig, dass die Schwerpunktkoordinaten der Elemente eindeutig sind, da sie unabhängig von der Raummetrik sind. Das heißt, der Rand des Laplace-Diagramms ist sowohl für das gerichtete als auch für das ungerichtete Diagramm symmetrisch (ich habe diesen Punkt nicht sofort erkannt). Schließlich kennen wir die Normen der Elemente der Basis (normalerweise sind sie in den Diagrammen gleich Null).

Es bleibt, alles Bekannte und Unbekannte in der Identität zu ersetzen, die Laplace und Gramian verbindet:

$$$Lm \ Gm = I$

Hier $$$I$ Ist eine Identitätsmatrix. In dieser Identität die Bedeutung des Übergangs von einem unvollständigen Laplace zu einem vollständigen.

Halt die Klappe und glaube

Gehen wir von Worten zu Taten über. So sieht der Laplace aus $$$L$ für ein Diagramm von zwei Knoten:

$$$L = \ begin {bmatrix} c_1 & -c_1 \\ c_2 & -c_2 \ end {bmatrix}$

Der Einfachheit halber haben wir die Beziehung mit Zahlen bezeichnet: $$$c_1 = c_ {AB}, c_2 = c_ {BA}$ . Es wird davon ausgegangen, dass die Werte der Anleihen bekannt sind - durch sie werden wir alle anderen Größen ausdrücken.

Voller Laplace $$$Lm$ enthält die Koordinaten des Orthozentrums $$$[rz, az, bz]$ ::

$$$Lm = \ begin {bmatrix} rz & az & bz \\ az & c_1 & -c_1 \\ bz & c_2 & -c_2 \ end {bmatrix}$

Hier $$$rz$ - die Norm des Orthozentrums (wird im symmetrischen Fall als Quadrat des Radius interpretiert), $$$az$ und $$$bz$ - Zersetzungskoeffizienten des Orthozentrums auf der Basis $$$A, B$ (Schwerpunktgewichte).

Volles Gramm $$$Gm$ Es sieht ungefähr so ​​aus:

$$$Gm = \ begin {bmatrix} 0 & za & zb \\ 1 & 0 & g_1 \\ 1 & g_2 & 0 \ end {bmatrix}$

Hier sind die Tupel $$$[za, zb]$ und $$$[1, 1]$ spiegeln die Doppelkoordinaten des Nullvektors wider. Diese Koordinaten sind Vernichter des Laplace (wenn sie mit dem Laplace multipliziert werden, ergeben sie einen Nullvektor - nicht zu verwechseln mit einem Nullvektor!).

Um das Problem zu lösen, müssen wir die Summe der Werte des Grammatikers finden: $$$- (g_1 + g_2)$ .

Wir betrachten die Anzahl der Unbekannten: $$$rz, az, bz, za, zb, g_1, g_2$ - nur 7 (ja, ja - um den Wert einer unglücklichen Entfernung herauszufinden, müssen wir sieben weitere zusätzliche Werte berechnen). Es gibt zwei bekannte Verbindungen am Eingang - $$$c_1$ und $$$c_2$ . Identität $$$Lm \ Gm = I$ wird 9 Gleichungen geben. Insgesamt 7 + 2 = 9, - alles konvergiert (überraschend). Es bleibt einfach das Gleichungssystem zu lösen.

Für ein Diagramm von zwei Knoten kann die Lösung (alle Unbekannten) in expliziter Form ausgedrückt werden. Wir geben endliche Ausdrücke für die Mengen, die uns interessieren. Wir führen das Konzept der allgemeinen geometrischen Konnektivität ein - dies ist der Kehrwert der Norm des orthogonalen Zentrums $$$gc = 1 / rz$ . Seine Dimension stimmt mit der Dimension der Diagrammverknüpfungen überein. Für einen Graphen von zwei Knoten (und zwei Verbindungen) hat die geometrische Verbindung einen schönen Ausdruck:

$$$gc = 1 / rz = (\ sqrt {c_1} + \ sqrt {c_2}) ^ 2$

Durch diese Verbindung kann man skalare Produkte von Knoten ausdrücken:

$$$g_1 = -gc \ sqrt {c_2}, \ quad g_2 = -gc \ sqrt {c_1}$

Sie können skalare Produkte übersetzen $$$g$ in gerichteten Abständen $$$s$ (3):

$$$s_ {BA} = gc \ sqrt {c_ {AB}}; \ quad s_ {BA} = gc \ sqrt {c_ {AB}}$

Der gewünschte kommutative Abstand zwischen Knoten wird durch die Summe bestimmt:

$$$S (A, B) = s_ {BA} + s_ {AB} = 1 / \ sqrt {c_ {AB} c_ {BA}} \ quad (4)$

Oma ist angekommen

Endlich. Ausdruck (4) - Dies ist die gewünschte Formel.

Der Abstand zwischen den Eckpunkten des Graphen zweier Knoten ist umgekehrt proportional zur Quadratwurzel des Produkts der Gegenverbindungen.

Sie können das Schulbuch mit einer anderen nutzlosen Formel laden.

Wenn die Verbindungen gleich sind, stimmt das Ergebnis mit dem Widerstandsabstand in den ungerichteten Diagrammen überein:

$$$S_ {c, c} (A, B) = 1 / c \ quad (4.1)$

Wir werden berechnen, was mit unserer Stadt da ist. Wenn Sie eine zweite Spur legen, verdoppelt sich die Kommunikation in eine Richtung. Dementsprechend ist die neue Entfernung $$$S_ {1, 2} (A, B)$ kann in Bezug auf das Original ausgedrückt werden:

$$$S_ {1, 2} (A, B) = 1 / \ sqrt {2 c_ {AB} c_ {BA}} = 1 / \ sqrt {2} S_ {1, 1} (A, B)$

Der Abstand zwischen den Bereichen verringert sich in $$$\ sqrt {2}$ mal. Es war offensichtlich, richtig?

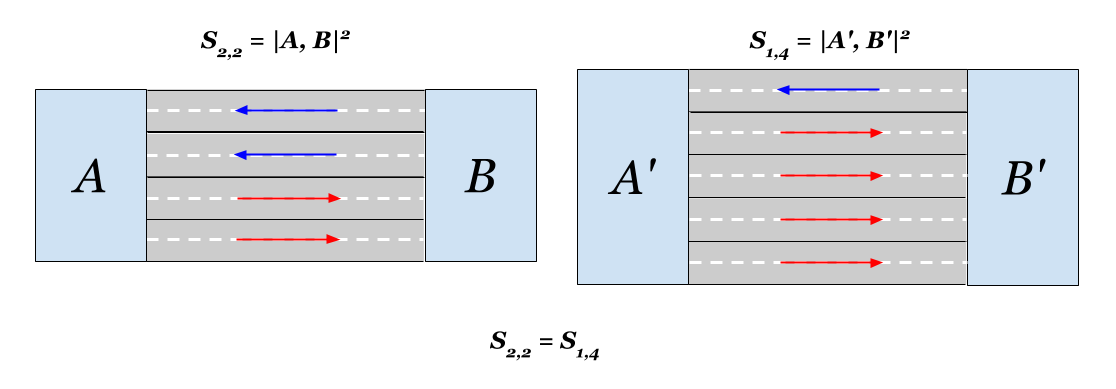
Es stellt sich auch heraus, dass in Bezug auf die Entfernung das Hinzufügen einer Spur zu jeder zweispurigen Straße auf jeder Seite dem Hinzufügen von drei Spuren auf einer Seite entspricht. Die euklidische Nähe wird sich in beiden Fällen verdoppeln. Interessant.



Das ist alles. Vielen Dank für Ihre Aufmerksamkeit.