Wo Beweise, Fakten und Vorstellungskraft zusammenlaufen

In der Mathematik, wo der Beweis alles ist, sind auch Fakten wichtig. Die Fakten sind jedoch nur dann gut, wenn das Modell gut ist und das Bauen von Modellen eine unzuverlässige Beschäftigung ist. Wie viele Fakten werden also ausreichen?

Kannst du die nächste Nummer in der Sequenz finden?

1, 2, 4, 8

Hier ist noch eine Nummer, wenn Sie mehr Daten benötigen, um eine Entscheidung zu treffen:

1, 2, 4, 8, 16

Die nächste Zahl sollte 32 sein, oder? Das Muster ist klar: Um die nächste Zahl zu finden, müssen Sie die vorherige verdoppeln. 1 × 2 = 2; 2 × 2 = 4; 4 × 2 = 8; 8 × 2 = 16. Die nächste Zahl sollte also 16 × 2 = 32 sein. Wie viele weitere Fakten werden benötigt, um dies zu bestätigen?

Obwohl anzunehmen ist, dass die nächste Zahl 32 ist, ist dies nicht immer der Fall. Betrachten Sie die folgende Reihenfolge: Wir zählen die Anzahl der Abschnitte, in die der Kreis durch Linien unterteilt ist, die Punkte auf einem Kreis verbinden.



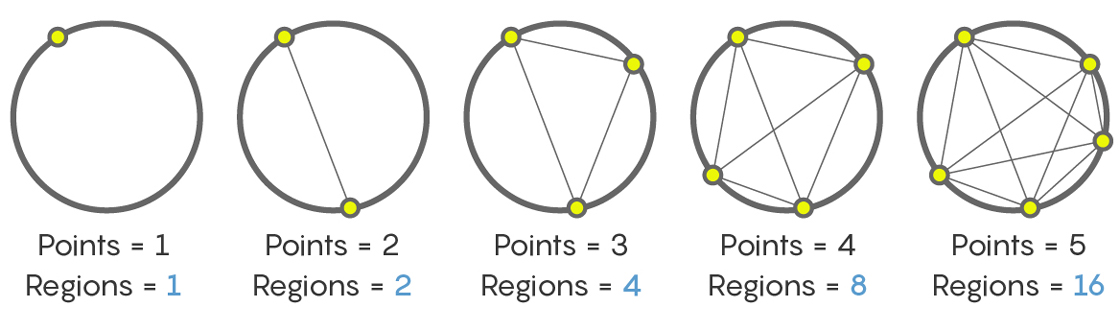
Ein Punkt ergibt einen Abschnitt (den gesamten inneren Teil des Kreises). Zwei Punkte - zwei Abschnitte. Drei Punkte - vier Abschnitte. Fünf und sechs sind acht bzw. sechzehn. Das Ergebnis ist eine Sequenz

1, 2, 4, 8, 16

Und wie viele Abschnitte werden angezeigt, nachdem die Linien von sechs Punkten auf dem Kreis verbunden wurden? Niemand wird Sie verurteilen, wenn Sie, wie viele Menschen, die zum ersten Mal vor dieser Aufgabe stehen, sagen, dass 32. Aber das ist nicht so. In der Tat, egal wie nervig, wird die Antwort sein - 31! Erzählen Sie sich selbst und überprüfen Sie es erneut.



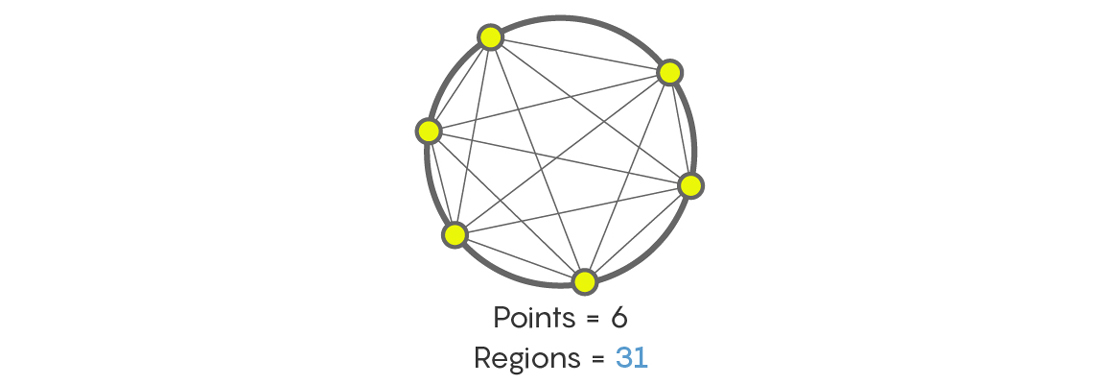
Natürlich gibt es Sequenzen wie 1, 2, 4, 8, 16, 32, 64 usw., wobei sich die Zahlen jedes Mal verdoppeln. Es gibt jedoch auch andere Sequenzen, z. B. die maximale Anzahl von Abschnitten, in die der Kreis durch Linien unterteilt ist, die die Punkte auf dem Kreis verbinden, und dies sind 1, 2, 4, 8, 16, 31, 57, 99 usw. Wenn wir die Sequenz 1, 2, 4, 8, 16 erfüllen, könnten wir denken, dass alle Fakten sind, dass die nächste Zahl 32 sein wird, aber es könnte etwas anderes geben.

Die Mathematik hat eine lange Tradition darin, unsere Erwartungen in Frage zu stellen und unsere Fantasie zum Funktionieren zu bringen. Deshalb bemühen sich Mathematiker immer um strenge Beweise, nicht nur um Fakten. Der Beweis begründet die mathematische Wahrheit. Alle Fakten mögen auf 32 als nächste Zahl in unserer Sequenz hinweisen, aber ohne strenge Beweise können wir uns dessen nicht sicher sein.

Dennoch sind Fakten für Mathematiker nützlich und wichtig. Bevor wir etwas beweisen, spielen wir oft mit den verfügbaren Informationen, untersuchen das Problem, betrachten Beispiele und sammeln Daten. Wir studieren und wägen die Fakten ab und entscheiden, was als nächstes zu tun ist. Diese Ergebnisse bilden unsere Meinung und schlagen vor, einige Theoreme zu beweisen und andere zu widerlegen.

Die Twin-Prime-Hypothese ist ein Beispiel, bei dem Fakten unser mathematisches Denken auf die gleiche Weise steuern wie Beweise. Zwillingsprimzahlen sind Paare von Primzahlen, die sich um 2 unterscheiden - zum Beispiel 3 und 5, 11 und 13, 101 und 103. Die Hypothese der Zwillingsprimzahlen legt nahe, dass es kein größtes Paar solcher Zwillinge gibt - das heißt, ähnlich Paare erscheinen ständig auf der Zahlenlinie, wenn sie sich ins Unendliche bewegen.

Die Twin-Prime-Hypothese ist kein Theorem, denn trotz der Tatsache, dass dies eines der bekanntesten Probleme in der Zahlentheorie ist, konnte es noch niemand beweisen. Fast jeder glaubt jedoch, dass es wahr ist, da es viele Fakten in seiner Unterstützung gibt.

Zum Beispiel finden wir bei unserer Suche nach Primzahlen ständig extrem große Paare von Zwillingsprimzahlen. Jede der Primzahlen des größten bekannten Paares enthält heute 400.000 Ziffern. Theoreme, die dieser Hypothese ähnlich sind, werden ebenfalls bewiesen. Im Jahr 2013 schockierte Zhang Ethan die mathematische Gemeinschaft, indem er das Vorhandensein einer unendlich großen Anzahl von Primzahlenpaaren nachwies, die sich um nicht mehr als 70 Millionen unterschieden. Dank des darauf folgenden offenen Polymath- Projekts wissen wir, dass es unendlich viele Primzahlenpaare gibt, die sich um nicht mehr als 246 unterscheiden . Wir haben die Existenz einer unendlichen Anzahl von Primzahlenpaaren, die sich um 2 unterscheiden, noch nicht bewiesen - aber 2 ist immer noch viel näher an 246 als 246 an unendlich.

Aus diesen und anderen Gründen ist der Glaube an Gerechtigkeit, auch wenn die Hypothese nicht bewiesen ist, nicht sehr umstritten. Es gibt jedoch auch andere Bereiche der Mathematik, in denen Fakten verwendet werden, um fundierte Meinungen zu bilden, die sich als kontroverser herausstellen.

Bei der Untersuchung elliptischer Kurven bezeichnet sein Rang grob gesagt eine numerische Schätzung der Komplexität der Lösung dieser Kurve. Viele Jahre lang wurde angenommen, dass die Ränge der elliptischen Kurven nicht begrenzt sind , dh es gibt keine Einschränkungen hinsichtlich des Werts des Ranges der Kurve oder der Komplexität der Lösung.

Neuere Arbeiten lassen Mathematiker jedoch über die Möglichkeit eines begrenzten Ranges nachdenken. Das Papier gibt Fakten an, die darauf hinweisen, dass es eine endliche Anzahl von Kurven gibt, deren Rang größer als 21 ist.

Vorsicht ist jedoch geboten. Die von Mathematikern gesammelten Fakten stammen nicht aus der Welt der elliptischen Kurven - sie beziehen sich auf die Matrizen, mit denen die Forscher die Kurven modellierten. Mathematische Modelle sind in der Wissenschaft weit verbreitet und können sogar nach innen gedreht werden, um Mathematik selbst zu studieren. Dies sind unglaublich leistungsstarke Tools, mit denen wir eine unverständliche Aufgabe durch eine ersetzen können, die für uns leichter zu bewältigen ist.

Die Verwendung von Modellen ist jedoch eine schwierige Angelegenheit. Sie können nie sicher sein, dass sich das Modell ganz ähnlich verhält wie das, was wir zu verstehen versuchen, damit wir aus seinem Verhalten Schlussfolgerungen ziehen können. Man kann auch nicht sicher sein, dass unser Modell genau an Orten von größter Bedeutung ähnlich ist. Daher ist es schwierig sicherzustellen, dass die Fakten, die wir auf der Grundlage von Modellen gesammelt haben, wirklich die realen Eigenschaften der Phänomene belegen, die wir untersuchen. Untersuchen wir diese Probleme anhand eines einfachen Modells einer einfachen Hypothese.

Stellen Sie sich vor, wir möchten die folgende Aussage untersuchen: Zwei beliebige Linien werden entweder geschnitten oder parallel.

Mit Schnittpunkt meinen wir das Vorhandensein von geraden Linien in gemeinsamen Punkten und mit Parallelität die Tatsache, dass sie in eine Richtung verlaufen, sich aber nicht schneiden (dieses Konzept kann anders definiert werden, aber ich werde dies der Einfachheit halber verwenden).

Erstellen Sie ein Modell, um dieses Problem zu untersuchen. Jede Linie wird durch die Gleichung der schrägen Linie dargestellt, an die Sie sich aus dem Schulkurs erinnern können. Das heißt, wir nehmen an, dass jede Linie durch eine Gleichung der Form beschrieben werden kann

y = mx + b

Dabei ist m die Steigung der Linie (ihre Steilheit) und b der Schnittpunkt der y-Achse (vertikale Achse).

Das Modellieren von Linien auf diese Weise ist praktisch für Experimente mit ihnen. Das Modell ermöglicht es uns, eine Zufallslinie zu erstellen, indem wir ein Paar von Zufallszahlen m und b auswählen. Wir können ein Paar zufälliger Linien auswählen und sie überprüfen - schneiden sie sich? Gehen sie einen Weg? Passiert noch etwas?

Hier sind einige Beispiele, wie die Ergebnisse solcher Experimente aussehen könnten.



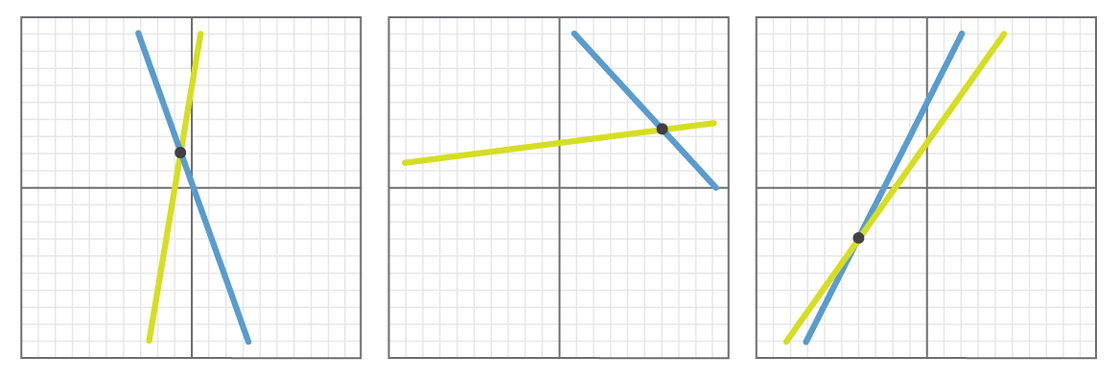
In jedem Beispiel schneiden sich zufällig ausgewählte Linien. Wenn wir dieses Experiment tausendmal durchführen - oder 10.000 oder eine Million -, werden wir feststellen, dass sich die Linien in allen Fällen schneiden oder parallel sind (und höchstwahrscheinlich alle Linien schneiden, da es unwahrscheinlich ist, dass die beiden Linien die gleiche Steigung haben, die gewählt wurde zufällig).

Wenn Sie sich eine Million Beispiele ansehen, können Sie daher zu dem Schluss kommen, dass die Hypothese höchstwahrscheinlich wahr ist. Alle Fakten stützen voll und ganz die Aussage, dass jedes Linienpaar entweder parallel ist oder sich schneidet.

Die Fakten sind jedoch nur so gut wie das Modell gut ist, und Modellierung ist gefährlich. Mal sehen, welche Gefahren wir uns in unserem Beispiel geschaffen haben.

Ein Problem ist, dass bestimmte Arten von Linien häufiger vorkommen als andere. Hier ist ein Diagramm mit 50 Linien mit b = 0 und 0 ≤ m ≤ 1.



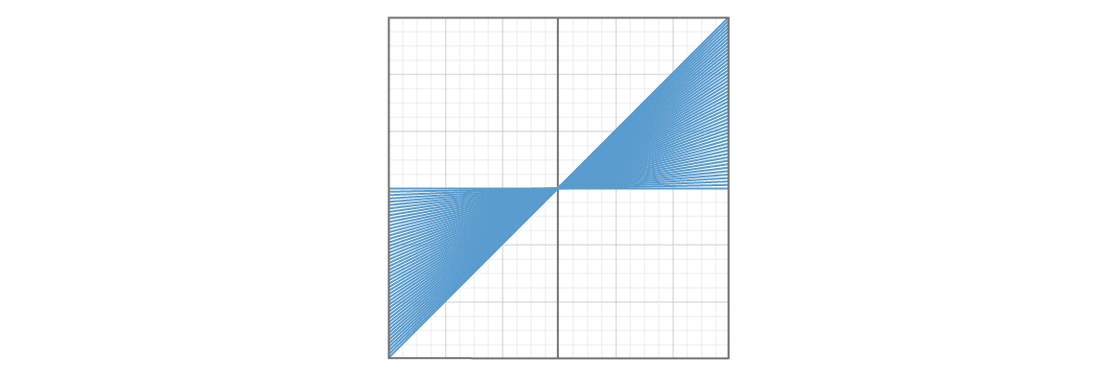
Und hier ist eine Grafik, die 50 Linien mit b = 0 und m ≥ 1 zeigt.



Es sieht so aus, als ob ein Viertel der Ebene mit geraden Linien mit einer Steigung von 0 bis 1 bedeckt ist, und ein anderes Viertel ist mit geraden Linien mit einer Steigung von mehr als 1 bedeckt. Die Auswahl einer Zahl größer als 1 scheint wahrscheinlicher als die Wahl einer Zahl von 0 bis 1, daher ist die Gerade wahrscheinlicher wird im zweiten Abschnitt des Flugzeugs sein. Dies bedeutet, dass bestimmte Linien mit einer Steigung von 0 bis 1 im Modell nur sehr wenig dargestellt werden. Und wenn in diesem Teil des Flugzeugs einige seltsame Dinge mit geraden Linien passieren, ist es unwahrscheinlich, dass unser Modell uns davon erzählt.

Wenn Sie sich das zweite Diagramm genau ansehen, werden wir ein weiteres Problem sehen. Je größer m wird, desto steiler werden die geraden Linien. Die coolste gerade Linie ist vertikal. Wie ist die Neigung der vertikalen Linie? Per Definition ist es nicht definiert: Es gibt keine solche Zahl m, die die vertikale Linie beschreiben könnte. Es stellt sich heraus, dass unser Modell keine vertikale Linie enthält und wir nicht damit experimentieren können. Wir haben noch nicht begonnen, Fakten zu sammeln, haben jedoch bereits einige Sonderfälle allein aufgrund des Modellbauplans ausgeschlossen.

Gleiches gilt für das schwerwiegendste Problem unseres Modells. Menschen, die sich den dreidimensionalen Raum leicht vorstellen können, haben wahrscheinlich sofort bemerkt, dass unsere Hypothese falsch ist. Eine gerade Linie muss sich nicht schneiden oder parallel sein. Stellen Sie sich zwei Korridore vor, die auf verschiedenen Etagen eines Gebäudes in unterschiedliche Richtungen verlaufen. Dies sind sich schneidende gerade Linien - gerade Linien, die sich nicht schneiden und nicht parallel sind.



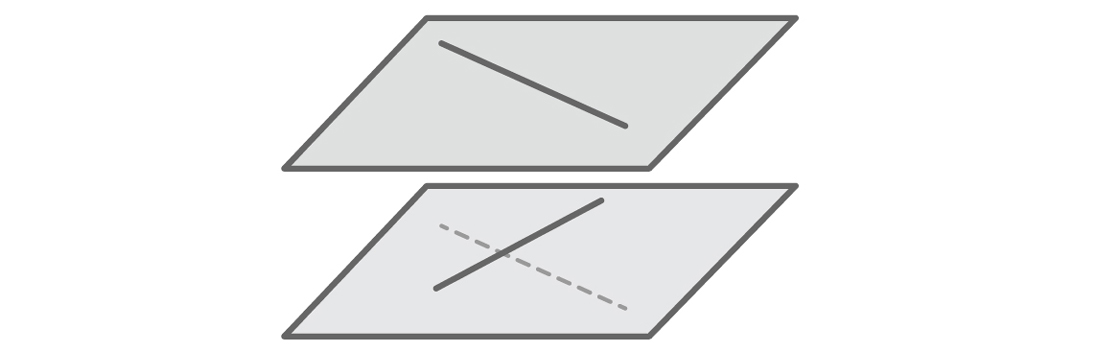
Kreuzlinien müssen in verschiedenen Ebenen liegen. Da unser Modell jedoch jede Linie durch die Gleichung y = mx + b definiert, stellen wir uns automatisch vor, dass sich alle Linien in derselben Ebene befinden. Unser Modell liefert nur Fakten, die unsere Hypothese stützen, denn wenn zwei Linien in derselben Ebene liegen, müssen sie sich tatsächlich entweder schneiden oder parallel verlaufen. Wir werden keine anderen Fakten sehen: In unserem Modell gibt es keine Schnittlinien. Wie bei vertikalen Linien schloss das Modell aus, was wir uns nicht vorstellen konnten.

Dies ist ein einfaches Beispiel für die Verwendung eines dummen Modells mit einer Reihe von Problemen, einschließlich kniffliger Fragen, wie z. B. der Auswahl von Zufallszahlen aus unendlichen Mengen. Professionelle Mathematiker, die die Reihen der elliptischen Kurven studieren, hätten niemals so vereinfachte und offensichtliche Fehler gemacht.

Diese Mathematiker wissen, welche Vorsichtsmaßnahmen bei der Arbeit mit Modellen zu treffen sind. Sie wissen, dass elliptische Kurven unabhängig davon, wie nützlich und interessant das Modell sein wird oder wie überzeugend die gesammelten Fakten sein werden, Eigenschaften offenbaren können, die sie sich nicht vorgestellt haben. Und wenn dies nicht vorstellbar ist, wird Ihr Modell dies nicht berücksichtigen, und daher werden die Fakten nicht reflektiert.

Aber ob das neue Modell richtig ist oder nicht, es zwang Mathematiker, produktiv über elliptische Kurven nachzudenken. Wenn es wirklich die Wahrheit widerspiegelt, können Ideen aus der Welt der Matrizen das Verhalten von Kurven erklären. Wenn nicht, kann das Verständnis, warum elliptische Kurven nicht auf diese Weise modelliert werden können, zu einem besseren Verständnis des Problems führen. Die Fakten, die wir sammeln, können uns auf die eine oder andere Weise dem Beweis näher bringen.