Quicklinks
-
Der Weg zu Version 12-
Zuerst etwas Mathe-
Der Kalkül der Unsicherheit-
Klassische Mathematik, Grundstufe und Fortgeschrittene-
Mehr mit Polygonen-
Rechnen mit Polyedern-
Euklidische Geometrie berechenbar gemacht-
Mit axiomatischen Theorien supersymbolisch werden-
Das n-Körper-Problem-
Spracherweiterungen und Annehmlichkeiten-
Weitere Superfunktionen für maschinelles Lernen-
Das Neueste in Neuronalen Netzen-
Rechnen mit Bildern-
Spracherkennung & mehr mit Audio-
Verarbeitung natürlicher Sprache-
Computerchemie-
Geografisches Rechnen erweitert-
Viele kleine Visualisierungsverbesserungen-
Verbesserung der Integration der Wissensdatenbank-
Integration von Big Data aus externen Datenbanken-
RDF, SPARQL und all das-
Numerische Optimierung-
Nichtlineare Finite-Elemente-Analyse-
Neuer, hoch entwickelter Compiler-
Aufruf von Python und anderen Sprachen-
Mehr für die Wolfram "Super Shell"-
Marionetten eines Webbrowsers-
Standalone-Mikrocontroller-
Aufrufen der Wolfram-Sprache von Python und anderen Orten aus-
Verbindung zum Einheitsuniversum-
Simulierte Umgebungen für maschinelles Lernen-
Blockchain- (und CryptoKitty-) Berechnung-
Und gewöhnliche Krypto auch-
Herstellen einer Verbindung zu Finanzdaten-Feeds-
Software Engineering & Plattform-Updates-
Und noch viel mehr ...
16. April 2019 - Stephen Wolfram
Heute veröffentlichen wir Version 12 von
Wolfram Language (und
Mathematica ) auf
Desktop-Plattformen und in der
Wolfram Cloud . Wir haben
Version 11.0 im August 2016 ,
11.1 im März 2017 ,
11.2 im September 2017 und
11.3 im März 2018 veröffentlicht . Es ist ein großer Sprung von Version 11.3 auf Version 12.0. Insgesamt gibt es
278 völlig neue Funktionen in vielleicht 103 Bereichen sowie Tausende verschiedener Updates im gesamten System:
In einer „
Integer-Version “ wie 12 ist es unser Ziel, vollständig ausgefüllte neue Funktionsbereiche bereitzustellen. In jeder Veröffentlichung möchten wir aber auch die neuesten Ergebnisse unserer Forschungs- und Entwicklungsbemühungen liefern. In 12.0 kann vielleicht die Hälfte unserer neuen Funktionen als Finishing-Bereiche betrachtet werden, die in früheren „.1“ -Versionen gestartet wurden - während die Hälfte neue Bereiche beginnt. Ich werde beide Arten von Funktionen in diesem Artikel diskutieren, aber ich werde besonders die Besonderheiten der Neuerungen von 11.3 auf 12.0 hervorheben.
Ich muss sagen, dass ich jetzt, da 12.0 fertig ist, erstaunt bin, wie viel darin enthalten ist und wie viel wir seit 11.3 hinzugefügt haben. In meiner Keynote auf unserer
Wolfram-Technologiekonferenz im vergangenen Oktober habe ich zusammengefasst, was wir bis zu diesem Zeitpunkt hatten - und selbst das dauerte fast 4 Stunden. Jetzt gibt es noch mehr.
Was wir konnten, ist ein Beweis sowohl für die Stärke unserer Forschungs- und Entwicklungsanstrengungen als auch für die Effektivität der Wolfram-Sprache als Entwicklungsumgebung. Beide Dinge bauen sich natürlich seit
drei Jahrzehnten auf . Neu bei 12.0 ist jedoch, dass wir die Leute unseren Designprozess hinter den Kulissen beobachten lassen -
mehr als 300 Stunden meiner internen Design-Meetings live übertragen. Zusätzlich zu allem anderen vermute ich, dass dies Version 12.0 zum allerersten großen Software-Release in der Geschichte macht, das auf diese Weise geöffnet wurde.
OK, was ist neu in 12.0? Es gibt einige große und überraschende Dinge - insbesondere in Bezug auf
Chemie ,
Geometrie ,
numerische Unsicherheit und
Datenbankintegration . Insgesamt gibt es jedoch viele Dinge in vielen Bereichen - und tatsächlich umfasst sogar die grundlegende Zusammenfassung im
Dokumentationszentrum bereits 19 Seiten:
Obwohl heutzutage die überwiegende Mehrheit dessen, was die Wolfram-Sprache (und Mathematica) tut, nicht das ist, was normalerweise als Mathematik angesehen wird, setzen wir immer noch enorme Forschungs- und Entwicklungsanstrengungen ein, um die Grenzen dessen zu erweitern, was in Mathematik getan werden kann. Und als erstes Beispiel für das, was wir in 12.0 hinzugefügt haben, ist hier der ziemlich farbenfrohe
ComplexPlot3D :
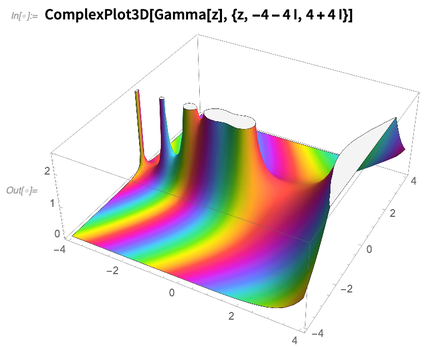
Es war immer möglich, Wolfram-Sprachcode zu schreiben, um Diagramme in der komplexen Ebene zu erstellen. Aber erst jetzt haben wir die mathematischen und algorithmischen Probleme gelöst, die erforderlich sind, um den Prozess der robusten Darstellung selbst recht pathologischer Funktionen in der komplexen Ebene zu automatisieren.
Ich erinnere mich, dass ich vor Jahren die
Dilogarithmusfunktion mit ihren Real- und Imaginärteilen
sorgfältig aufgezeichnet habe . Jetzt macht
ReImPlot es einfach:
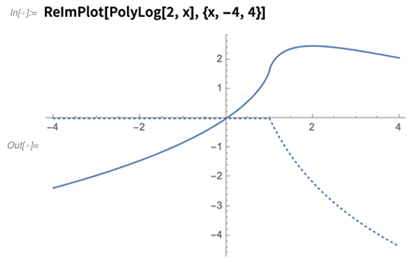
Die Visualisierung komplexer Funktionen ist (Wortspiel beiseite) eine komplexe Geschichte, wobei Details einen großen Unterschied darin machen, was man über eine Funktion bemerkt. Eines der Dinge, die wir in 12.0 getan haben, ist die Einführung sorgfältig ausgewählter standardisierter Methoden (z. B. benannte
Farbfunktionen ), um verschiedene Funktionen hervorzuheben:
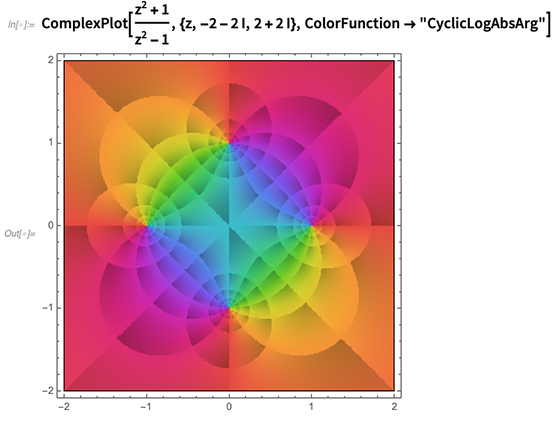
Der Kalkül der Unsicherheit
Messungen in der realen Welt weisen häufig Unsicherheiten auf, die als Werte mit ± Fehlern dargestellt werden. Wir haben seit Ewigkeiten Add-On-Pakete für den Umgang mit „Zahlen mit Fehlern“. Aber in Version 12.0 bauen wir Berechnungen mit Unsicherheit ein und machen es richtig.
Der Schlüssel ist das symbolische Objekt
um [
x, δ ], das einen Wert "um
x " mit der Unsicherheit
δ darstellt :
Mit
Around können Sie rechnen, und es gibt eine ganze Rechnung darüber, wie sich die Unsicherheiten verbinden:
Wenn Sie
um Zahlen zeichnen, werden diese mit Fehlerbalken angezeigt:
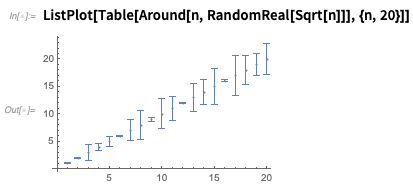
Es gibt viele Optionen - wie hier ist eine Möglichkeit, Unsicherheit sowohl in
x als auch in
y zu zeigen:
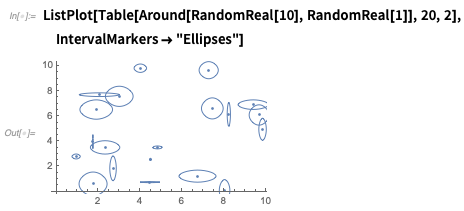
Sie können
um Mengen haben:
Und Sie können auch symbolische
Around- Objekte haben:
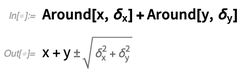
Aber was ist eigentlich ein
Around- Objekt? Hier gibt es bestimmte Regeln zum Kombinieren von Unsicherheiten, die auf unkorrelierten Normalverteilungen basieren. Es wird jedoch keine Aussage getroffen, dass
Around [
x, δ ] etwas darstellt, das tatsächlich im Detail einer Normalverteilung folgt - ebenso wenig wie
Around [
x, δ ] eine Zahl darstellt, die spezifisch in dem durch
Intervall [{
x - δ, x + δ }]. Es ist nur so, dass
Around- Objekte ihre Fehler oder Unsicherheiten nach einheitlichen allgemeinen Regeln verbreiten, die erfolgreich erfassen, was in der experimentellen Wissenschaft normalerweise getan wird.
OK, nehmen wir an, Sie führen eine Reihe von Messungen mit einem bestimmten Wert durch. Mit
MeanAround können Sie eine Schätzung des Werts - zusammen mit seiner Unsicherheit -
erhalten (und wenn die Messungen selbst Unsicherheiten aufweisen, werden diese bei der Gewichtung ihrer Beiträge berücksichtigt):
Funktionen im gesamten System - insbesondere beim
maschinellen Lernen - haben ab
sofort die Option
ComputeUncertainty ->
True , wodurch sie eher
Around- Objekte als reine Zahlen
angeben .
Herum mag wie ein einfaches Konzept erscheinen, aber es ist voller Feinheiten - was der Hauptgrund ist, warum es bisher gebraucht wurde, um in das System zu gelangen. Viele der Feinheiten drehen sich um Korrelationen zwischen Unsicherheiten. Die Grundidee ist, dass die Unsicherheit jedes
Around- Objekts als unabhängig angenommen wird. Aber manchmal hat man Werte mit korrelierten Unsicherheiten - und so gibt es neben
Around auch
VectorAround , das einen Vektor potenziell korrelierter Werte mit einer bestimmten Kovarianzmatrix darstellt.
Es ist noch subtiler, wenn man sich mit Dingen wie algebraischen Formeln befasst. Wenn man hier x durch ein
Around ersetzt , wird nach den Regeln von
Around angenommen , dass jede Instanz nicht korreliert ist:
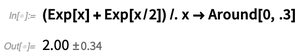
Aber wahrscheinlich möchte man hier annehmen, dass der Wert von x zwar ungewiss ist, aber für jede Instanz gleich ist, und man kann dies mit der Funktion
AroundReplace tun (beachten Sie, dass das Ergebnis anders ist):
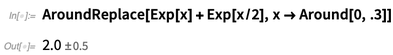
Es ist sehr subtil, unsichere Zahlen anzuzeigen. Wie viele nachgestellte Nullen sollten Sie eingeben:
Oder wie genau die Unsicherheit der Unsicherheit sein sollte (es gibt einen herkömmlichen Haltepunkt, wenn die nachfolgenden Ziffern 35 sind):
In seltenen Fällen, in denen viele Ziffern bekannt sind (z. B. einige
physikalische Konstanten ), möchte man einen anderen Weg gehen, um die Unsicherheit zu spezifizieren:
Und es geht weiter und weiter. Aber allmählich wird
Around im ganzen System auftauchen. Übrigens gibt es viele andere Möglichkeiten,
um Zahlen anzugeben. Dies ist eine Zahl mit einem relativen Fehler von 10%:
Dies ist das Beste, was
Around tun kann, um ein Intervall darzustellen:
Für eine
Verteilung berechnet
Around die Varianz:
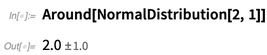
Es kann auch Asymmetrie berücksichtigen, indem asymmetrische Unsicherheiten angegeben werden:
Klassische Mathematik, Grundstufe und Fortgeschrittene
Bei der Berechnung von Mathematik ist es immer eine Herausforderung, sowohl „alles richtig zu machen“ als auch elementare Benutzer nicht zu verwirren oder einzuschüchtern. In Version 12.0 werden verschiedene Hilfestellungen vorgestellt. Versuchen Sie zunächst, eine irreduzible
Quintgleichung zu lösen :
In der Vergangenheit hätte dies eine Reihe expliziter
Root- Objekte gezeigt. Jetzt werden die
Root- Objekte als Kästchen formatiert, in denen ihre ungefähren numerischen Werte angezeigt werden. Berechnungen funktionieren genauso, aber das Display konfrontiert die Leute nicht sofort damit, über algebraische Zahlen Bescheid zu wissen.
Wenn wir
Integrieren sagen, meinen wir „ein Integral finden“ im Sinne eines Antiderivativs. Aber in der Elementarrechnung wollen die Leute explizite Integrationskonstanten sehen (wie immer in
Wolfram | Alpha ), deshalb haben wir
eine Option dafür hinzugefügt (und C [
n ] hat auch eine schöne, neue Ausgabeform):
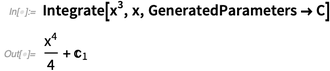
Wenn wir unsere symbolischen Integrationsfähigkeiten vergleichen, machen wir das wirklich gut. Es kann jedoch immer mehr getan werden, insbesondere um die einfachsten Formen von Integralen zu finden (und auf theoretischer Ebene ist dies eine unvermeidliche Folge der Unentscheidbarkeit der Äquivalenz symbolischer Ausdrücke). In Version 12.0 haben wir weiterhin an der Grenze gearbeitet und Fälle hinzugefügt wie:
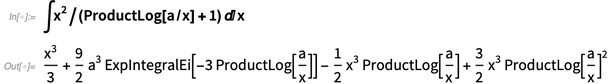
In Version 11.3 haben wir die asymptotische Analyse eingeführt, um asymptotische Werte von Integralen usw. zu finden. Version 12.0 fügt asymptotische Summen, asymptotische Rezidive und asymptotische Lösungen zu Gleichungen hinzu:
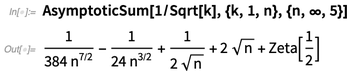
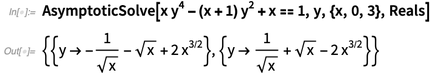
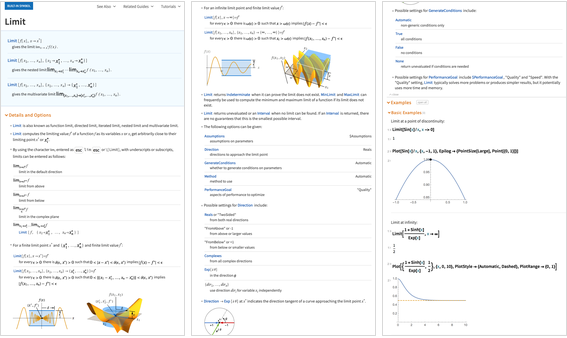
Eines der großartigen Dinge bei der Berechnung von Mathematik ist, dass es uns neue Möglichkeiten gibt, Mathematik selbst zu erklären. Wir haben unsere Dokumentation so erweitert, dass sie sowohl die Mathematik als auch die Funktionen erklärt. Hier ist zum Beispiel der Beginn der Dokumentation zu
Limit - mit Diagrammen und Beispielen der wichtigsten mathematischen Ideen:
Polygone sind seit Version 1 Teil der Wolfram-Sprache. In Version 12.0 werden sie jedoch verallgemeinert: Jetzt gibt es eine systematische Möglichkeit, Löcher in ihnen anzugeben. Ein klassischer geografischer Anwendungsfall ist das Polygon für
Südafrika - mit seinem Loch für das Land
Lesotho .
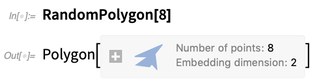
In Version 12.0 erhält
Polygon ähnlich wie
Root ein praktisches neues Anzeigeformular:
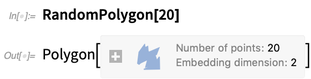
Sie können damit wie zuvor rechnen:
RandomPolygon ist ebenfalls neu. Sie können beispielsweise nach 5 zufälligen konvexen Polygonen mit jeweils 10 Eckpunkten in 3D fragen:
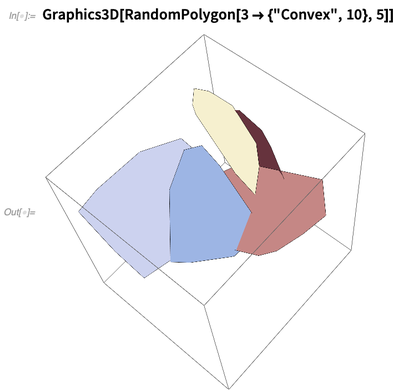
Es gibt viele neue Operationen für Polygone. Wie
PolygonDecomposition , mit der beispielsweise ein Polygon in konvexe Teile zerlegt werden kann:
Polygone mit Löchern erfordern auch andere Arten von Operationen, wie
z. B.
OuterPolygon ,
SimplePolygonQ und
CanonicalizePolygon .
Polygone sind ziemlich einfach anzugeben: Sie geben nur ihre Scheitelpunkte in der richtigen Reihenfolge an (und wenn sie Löcher haben, geben Sie auch die Scheitelpunkte für die Löcher an). Polyeder sind etwas komplizierter: Zusätzlich zu den Scheitelpunkten müssen Sie angeben, wie diese Scheitelpunkte Flächen bilden. In Version 12.0 können Sie dies mit
Polyhedron jedoch allgemein tun, einschließlich Hohlräumen (dem 3D-Analogon von Löchern) usw.
In Version 12.0 werden jedoch Funktionen für die fünf
platonischen Körper eingeführt, die ihre über
2000-jährige Geschichte erkennen:
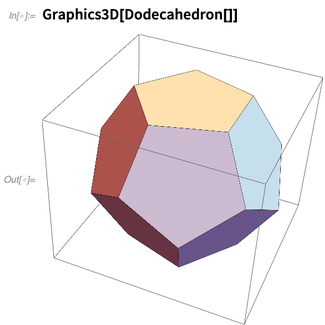
Und angesichts der platonischen Körper kann man sofort mit dem Rechnen beginnen:
Hier ist der Raumwinkel am Scheitelpunkt 1 (da er platonisch ist, geben alle Scheitelpunkte den gleichen Winkel an):
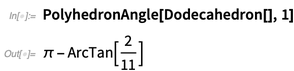
Hier ist eine Operation am Polyeder:
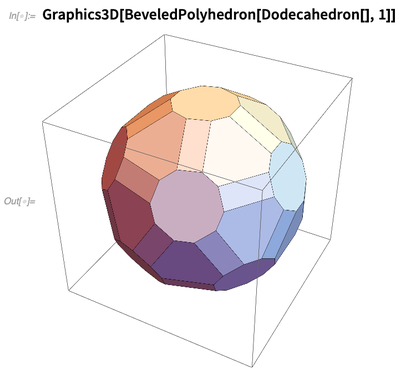
Über die platonischen Körper hinaus baut Version 12 auch alle „
einheitlichen Polyeder “ ein (
n Kanten und
m Flächen treffen sich an jedem Scheitelpunkt) - und Sie können auch symbolische
Polyederversionen benannter Polyeder von
PolyhedronData erhalten :
Sie können jedes beliebige Polyeder (einschließlich eines „zufälligen“ mit
RandomPolyhedron )
erstellen und dann die gewünschten Berechnungen durchführen:
Mathematica und die Wolfram-Sprache sind sehr mächtig darin, sowohl explizite
Rechengeometrie als auch
in Bezug auf Algebra dargestellte Geometrie zu erstellen . Aber was ist mit der Geometrie, wie sie in
Euklids Elementen gemacht wird - in der man geometrische Aussagen macht und dann sieht, was ihre Konsequenzen sind?
Nun, in Version 12 können wir mit dem gesamten Turm der Technologie, den wir gebaut haben, endlich einen neuen Stil der mathematischen Berechnung liefern - der tatsächlich automatisiert, was Euclid vor über 2000 Jahren tat. Eine Schlüsselidee besteht darin, symbolische „geometrische Szenen“ einzuführen, deren Symbole Konstrukte wie Punkte darstellen, und dann geometrische Objekte und Beziehungen in Bezug auf diese zu definieren.
Hier ist zum Beispiel eine geometrische Szene, die ein Dreieck
a, b, c und einen Kreis durch
a, b und
c mit dem Mittelpunkt
o darstellt , mit der Einschränkung, dass
o am Mittelpunkt der Linie von
a nach
c liegt :
Für sich genommen ist dies nur eine symbolische Sache. Aber wir können Operationen daran durchführen. Zum Beispiel können wir nach einer zufälligen Instanz fragen, in der
a, b, c und
o spezifisch gemacht werden:
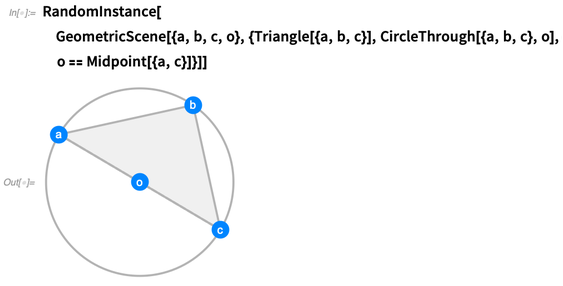
Sie können so viele zufällige Instanzen generieren, wie Sie möchten. Wir versuchen, die Instanzen so allgemein wie möglich zu gestalten, ohne Zufälle, die nicht durch die Einschränkungen erzwungen werden:
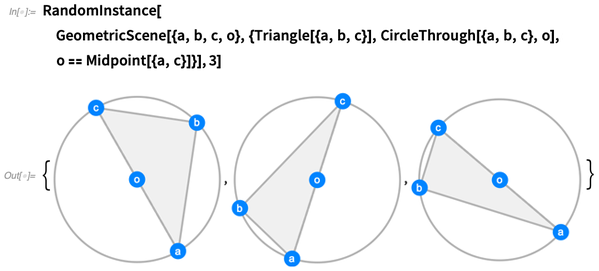
OK, aber jetzt lass uns "Euklid spielen" und geometrische Vermutungen finden, die mit unserem Setup übereinstimmen:
Für eine gegebene geometrische Szene kann es viele mögliche Vermutungen geben. Wir versuchen die interessanten herauszusuchen. In diesem Fall kommen wir auf zwei - und was dargestellt ist, ist die erste: dass die Linie ba senkrecht zur Linie cb ist. Zufällig erscheint dieses Ergebnis tatsächlich in Euklid (es ist in
Buch 3 als Teil von Satz 31 ) - obwohl es normalerweise
Thales 'Theorem genannt wird .
In 12.0 haben wir jetzt eine ganze symbolische Sprache zur Darstellung typischer Dinge, die in der Euklid-Geometrie vorkommen. Hier ist eine komplexere Situation - entsprechend
dem Satz von Napoleon :
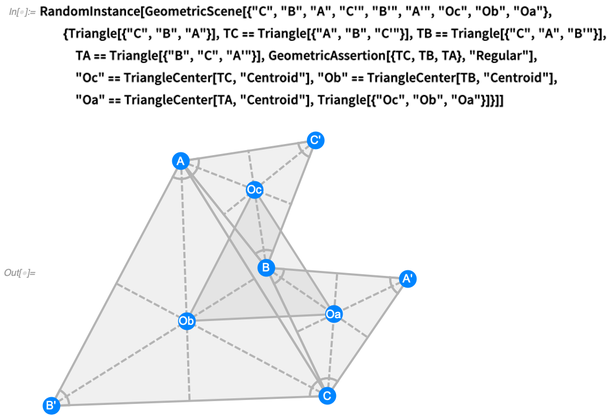
In 12.0 gibt es viele neue und nützliche geometrische Funktionen, die mit expliziten Koordinaten arbeiten:
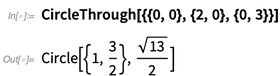
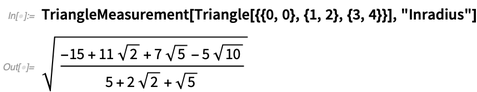
Für Dreiecke werden 12 Arten von "Zentren" unterstützt, und ja, es kann symbolische Koordinaten geben:
Und um das Einrichten geometrischer Aussagen zu unterstützen, benötigen wir auch „
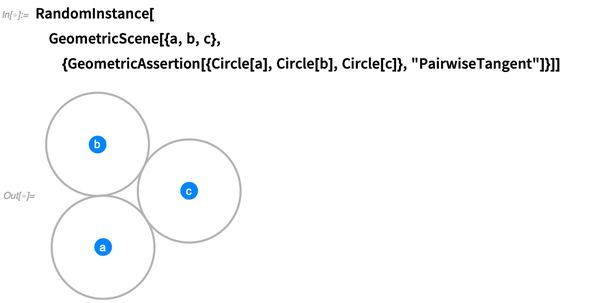
geometrische Aussagen “. In 12.0 gibt es 29 verschiedene Arten - wie
"Parallel" ,
"Kongruent" ,
"Tangens" ,
"Konvex" usw. Hier sind drei Kreise, von denen behauptet wird, dass sie paarweise tangential sind:
Mit axiomatischen Theorien supersymbolisch werden
In Version 11.3 wurde
FindEquationalProof zum Generieren symbolischer Darstellungen von Beweisen eingeführt. Aber welche Axiome sollten für diese Beweise verwendet werden? In Version 12.0 wird
AxiomaticTheory eingeführt, die Axiome für verschiedene gängige
axiomatische Theorien enthält .
Hier ist mein
persönliches Lieblingsaxiomensystem :
Was bedeutet das? In gewisser Hinsicht ist es ein symbolischerer symbolischer Ausdruck als wir es gewohnt sind. In so etwas wie 1 +
x sagen wir nicht, was der Wert von
x ist, aber wir stellen uns vor, dass es einen Wert haben kann. Im obigen Ausdruck sind a, b und c reine „formale Symbole“, die eine im Wesentlichen strukturelle Rolle spielen und niemals als konkrete Werte angesehen werden können.
Was ist mit dem · (Mittelpunkt)? In 1 +
x wissen wir, was + bedeutet. Das · soll aber ein rein abstrakter Operator sein. Der Punkt des Axioms besteht darin
, eine Einschränkung für das zu
definieren, was · darstellen kann. In diesem speziellen Fall stellt sich heraus, dass das Axiom ein
Axiom für die Boolesche Algebra ist , so dass
Nand und
Nor dargestellt werden können . Aber wir können die Konsequenzen des Axioms vollständig formal ableiten, zum Beispiel mit
FindEquationalProof :
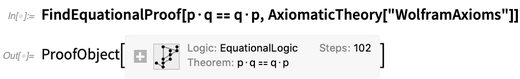
In all dem steckt einiges an Subtilität. Im obigen Beispiel ist es nützlich, · als Operator zu haben, nicht zuletzt, weil es gut angezeigt wird. Aber es gibt keine eingebaute Bedeutung, und mit
AxiomaticTheory können Sie als Operator etwas anderes (hier
f ) angeben:
Was macht der
"Nand" dort? Es ist ein Name für den Operator (aber er sollte nicht als etwas interpretiert werden, das mit dem Wert des Operators zu tun hat). In den
Axiomen für die Gruppentheorie erscheinen beispielsweise mehrere Operatoren:
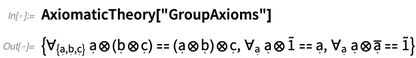
Dies gibt die Standarddarstellungen der verschiedenen Operatoren hier:
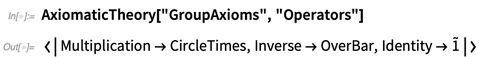AxiomaticTheory kennt bemerkenswerte Theoreme für bestimmte axiomatische Systeme:
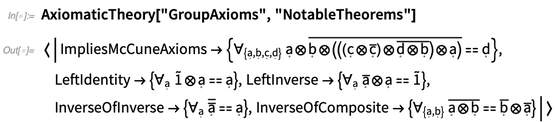
Die Grundidee formaler Symbole wurde in Version 7 eingeführt, um beispielsweise Dummy-Variablen in generierten Konstrukten wie diesen darzustellen:
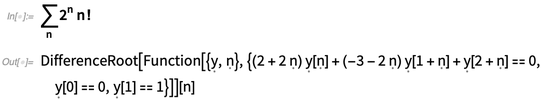
Sie können ein formales Symbol mit
\ [FormalA] oder Esc, a, Esc usw.
eingeben . Aber zurück in Version 7,
\ [FormalA] wurde als gerendert. Und das bedeutete, dass der obige Ausdruck so aussah:
Ich fand das immer unglaublich kompliziert. Und für Version 12 wollten wir es vereinfachen. Wir haben viele Möglichkeiten ausprobiert, uns aber schließlich für einzelne graue Unterpunkte entschieden - was meiner Meinung nach viel besser aussieht.
In
AxiomaticTheory sind sowohl die Variablen als auch die Operatoren „rein symbolisch“. Aber eine Sache, die definitiv ist, ist die Arität jedes Operators, die man
AxiomaticTheory fragen kann:
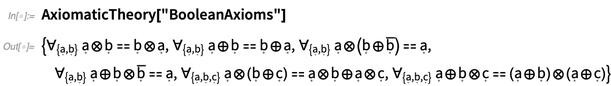
Praktischerweise kann die Darstellung von Operatoren und Aritäten sofort in
Gruppierungen eingespeist werden, um mögliche Ausdrücke mit bestimmten Variablen zu erhalten:
Das n- Körper-Problem
Axiomatische Theorien stellen einen klassischen historischen Bereich für die Mathematik dar. Ein weiteres klassisches historisches Gebiet - viel mehr auf der angewandten Seite - ist das
n- Körper-Problem . In Version 12.0 wird
NBodySimulation eingeführt, mit dem das n-Körper-Problem simuliert werden kann. Hier ist ein Drei-Körper-Problem (denken Sie an
Erde-Mond-Sonne ) mit bestimmten Anfangsbedingungen (und dem Gesetz der inversen quadratischen Kraft):
Sie können nach verschiedenen Aspekten der Lösung fragen. Dies zeigt die Positionen als Funktion der Zeit:
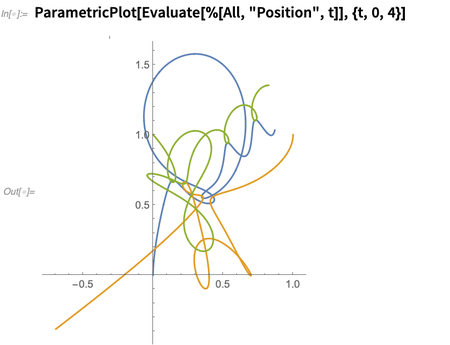
Darunter werden nur Differentialgleichungen gelöst, aber - ähnlich wie bei
SystemModel - bietet
NBodySimulation eine bequeme Möglichkeit, die Gleichungen einzurichten und ihre Lösungen zu handhaben. Und ja, Standard-Kraftgesetze sind eingebaut, aber Sie können Ihre eigenen definieren.
Spracherweiterungen und Annehmlichkeiten
Wir polieren seit mehr als 30 Jahren den Kern der Wolfram-Sprache und führen in jeder nachfolgenden Version einige neue Erweiterungen und Annehmlichkeiten ein.
Wir haben die Funktion
Information seit Version 1.0, aber in 12.0 haben wir sie stark erweitert. Früher gab es nur Informationen zu Symbolen (obwohl diese ebenfalls modernisiert wurden):
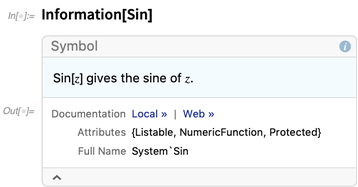
Jetzt gibt es aber auch Informationen über viele Arten von Objekten. Hier sind Informationen zu einem Klassifikator:
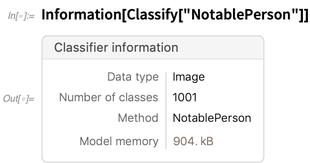
Hier sind Informationen zu einem Cloud-Objekt:
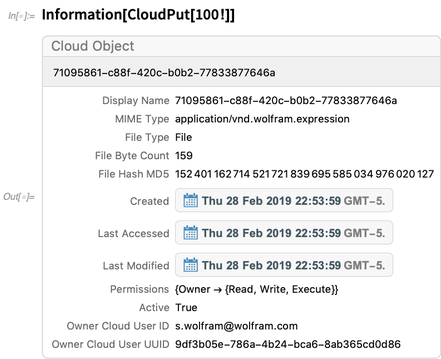
Bewegen Sie den Mauszeiger über die Beschriftungen im „Informationsfeld“ und Sie können die Namen der entsprechenden Eigenschaften herausfinden:
Für Entitäten gibt
Information eine Zusammenfassung bekannter Eigenschaftswerte:
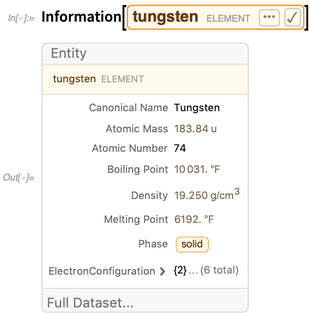
In den letzten Versionen haben wir viele neue Formulare für die Anzeige von Zusammenfassungen eingeführt. In Version 11.3 haben wir
Iconize eingeführt, mit dem im Wesentlichen ein zusammenfassendes Anzeigeformular für alles erstellt werden kann. Iconize hat sich als noch nützlicher erwiesen, als wir ursprünglich erwartet hatten. Es ist großartig, um unnötige Komplexität sowohl in Notizbüchern als auch in Teilen des Wolfram-Sprachcodes zu verbergen. In 12.0 haben wir die Anzeige von Iconize neu gestaltet, insbesondere, damit sie in Ausdrücken und Code „gut gelesen“ werden kann.
Sie können etwas explizit symbolisieren:
Drücken Sie das + und Sie sehen einige Details:
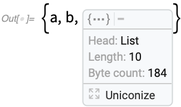
Drücken Sie
und Sie erhalten wieder den ursprünglichen Ausdruck:
Wenn Sie viele Daten haben, auf die Sie in einer Berechnung verweisen möchten, können Sie diese jederzeit in einer Datei oder in der
Cloud (oder sogar in einem
Datenrepository )
speichern . In der Regel ist es jedoch bequemer, es einfach in Ihr Notizbuch zu legen, damit Sie alles am selben Ort haben. Eine Möglichkeit, die Daten zu vermeiden, die Ihr Notebook übernehmen, besteht darin,
sie in geschlossene Zellen zu
legen . Iconize bietet jedoch eine viel flexiblere und elegantere Möglichkeit, dies zu tun.
Wenn Sie Code schreiben, ist es oft praktisch, „an Ort und Stelle zu symbolisieren“. Mit dem Kontextmenü können Sie jetzt Folgendes tun:
Apropos Anzeige, hier ist etwas Kleines, aber Praktisches, das wir in 12.0 hinzugefügt haben:
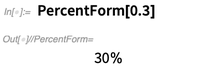
Und hier sind ein paar andere "Zahlen-Annehmlichkeiten", die wir hinzugefügt haben:
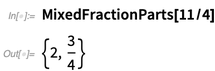
Funktionale Programmierung war schon immer ein zentraler Bestandteil der Wolfram-Sprache. Wir sind jedoch ständig bemüht, es zu erweitern und neue, allgemein nützliche Grundelemente einzuführen. Ein Beispiel in Version 12.0 ist
SubsetMap :
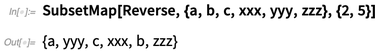
Funktionen sind normalerweise Dinge, die mehrere Eingaben annehmen können, aber immer eine einzige Ausgabe liefern. In Bereichen wie dem
Quantencomputer ist man jedoch daran interessiert,
n Ein- und
n Ausgänge zu haben.
SubsetMap implementiert effektiv
n-> n Funktionen, nimmt Eingaben von
n angegebenen Positionen in einer Liste auf, wendet eine Operation auf diese an und setzt die Ergebnisse an denselben
n Positionen zurück.
Ich
habe vor ungefähr einem Jahr angefangen zu formulieren, was jetzt
SubsetMap ist. Und mir wurde schnell klar, dass ich diese Funktion im Laufe der Jahre tatsächlich an allen möglichen Orten hätte nutzen können. Aber wie soll dieser besondere „Klumpen Rechenarbeit“ genannt werden? Mein ursprünglicher Arbeitsname war
ArrayReplaceFunction (den ich in meinen Notizen auf
ARF abgekürzt habe). In einer
Folge von (Livestream-) Meetings gingen wir hin und her. Es gab Ideen wie
ApplyAt (aber es ist nicht wirklich
Apply ) und
MutateAt (aber es macht keine Mutation im lvalue-Sinne) sowie
RewriteAt ,
ReplaceAt ,
MultipartApply und
ConstructInPlace . Es gab Ideen zu Curry-Formularen für „Funktionsdekorateure“ wie
PartAppliedFunction ,
PartwiseFunction ,
AppliedOnto ,
AppliedAcross und
MultipartCurry .
Aber irgendwie, als wir die Funktion erklärten, kamen wir immer wieder darauf zurück, darüber zu sprechen, wie sie auf einer Teilmenge einer Liste funktioniert und wie sie wirklich wie
Map ist , außer dass sie auf mehreren Elementen gleichzeitig funktioniert. Also haben wir uns endlich für den Namen
SubsetMap entschieden . Und - in einer weiteren Bestätigung der Bedeutung des Sprachdesigns - ist es bemerkenswert, wie man, sobald man einen Namen für so etwas hat, sofort in der Lage ist, darüber nachzudenken und zu sehen, wo es verwendet werden kann.
Seit vielen Jahren arbeiten wir hart daran, die Wolfram-Sprache zum höchsten und automatisiertesten System für
maschinelles Lernen auf dem neuesten
Stand der Technik zu machen . Schon früh haben wir die „Superfunktionen“
Klassifizieren und
Vorhersagen eingeführt , die
Klassifizierungs- und Vorhersageaufgaben vollständig automatisiert ausführen und automatisch den besten Ansatz für die jeweilige Eingabe auswählen. Auf dem Weg haben wir andere Superfunktionen eingeführt - wie
SequencePredict ,
ActiveClassification und
FeatureExtract .
In Version 12.0 haben wir einige wichtige neue Superfunktionen für maschinelles Lernen. Es gibt
FindAnomalies , die "anomale Elemente" in Daten finden:
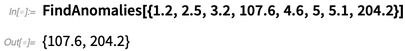
Zusammen mit diesem gibt es
DeleteAnomalies , das Elemente löscht, die es für anomal hält:
Es gibt auch
SynthesizeMissingValues , die versuchen, plausible Werte für fehlende Daten zu generieren:
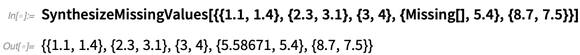
Wie funktionieren diese Funktionen? Sie basieren alle auf einer neuen Funktion namens
LearnDistribution , die
anhand einer Reihe von Beispielen versucht, die zugrunde liegende Verteilung von Daten zu lernen. Wenn die Beispiele nur Zahlen wären, wäre dies im Wesentlichen ein Standardstatistikproblem, für das wir so etwas wie
EstimatedDistribution verwenden könnten. Der Punkt bei
LearnDistribution ist jedoch, dass es mit Daten jeglicher Art funktioniert, nicht nur mit Zahlen. Hier lernt es eine zugrunde liegende Verteilung für eine Sammlung von Farben:
Sobald wir diese „gelernte Verteilung“ haben, können wir alle möglichen Dinge damit machen. Dies generiert beispielsweise 20 Zufallsstichproben daraus:
Aber denken
Sie jetzt an
FindAnomalies . Es muss herausgefunden werden, welche Datenpunkte im Verhältnis zu den erwarteten Daten anomal sind. Mit anderen Worten, angesichts der zugrunde liegenden Verteilung der Daten wird ermittelt, welche Datenpunkte Ausreißer sind, in dem Sinne, dass sie gemäß der Verteilung nur mit sehr geringer Wahrscheinlichkeit auftreten sollten.
Und genau wie bei einer normalen numerischen Verteilung können wir das
PDF für ein bestimmtes Datenelement berechnen. Lila ist angesichts der Verteilung der Farben, die wir aus unseren Beispielen gelernt haben, ziemlich wahrscheinlich:
Aber Rot ist wirklich sehr, sehr unwahrscheinlich:
Für gewöhnliche numerische Verteilungen gibt es Konzepte wie
CDF , die uns kumulative Wahrscheinlichkeiten mitteilen, dass wir Ergebnisse erhalten, die „weiter entfernt“ als ein bestimmter Wert sind. Für Räume willkürlicher Dinge gibt es nicht wirklich den Begriff „weiter draußen“. Wir haben uns jedoch eine Funktion
ausgedacht , die wir
RarerProbability nennen.
Sie gibt an , wie
hoch die Gesamtwahrscheinlichkeit ist, ein Beispiel mit einer kleineren PDF-Datei als der von uns angegebenen zu generieren:
Jetzt haben wir eine Möglichkeit, Anomalien zu beschreiben: Es handelt sich nur um Datenpunkte mit einer sehr geringen Wahrscheinlichkeit. Tatsächlich verfügt
FindAnomalies über eine Option
AcceptanceThreshold (mit dem Standardwert 0,001), die angibt, was als "sehr klein" gelten soll.
OK, aber sehen wir uns diese Arbeit an etwas Komplizierterem als Farben an. Lassen Sie uns einen Anomaliedetektor anhand von 1000 Beispielen handgeschriebener Ziffern trainieren:
Jetzt können
FindAnomalies uns sagen, welche Beispiele anomal sind:
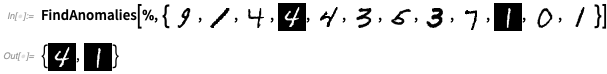
Wir haben bereits 2016 als Teil von Version 11 unser symbolisches Framework für den Aufbau, die Erforschung und Verwendung neuronaler Netze eingeführt. Seitdem haben wir in jeder Version alle möglichen Funktionen auf dem neuesten Stand der Technik hinzugefügt. Im Juni 2018 haben wir unser
neuronales Netz-Repository eingeführt , um den Zugriff auf die neuesten neuronalen Netzmodelle aus der Wolfram-Sprache zu vereinfachen. Es befinden sich bereits fast 100 kuratierte Modelle verschiedener Typen im Repository, wobei ständig neue hinzugefügt werden.
Wenn Sie also das neueste
neuronale BERT-Transformator-Netzwerk benötigen (das heute hinzugefügt wurde!),
Können Sie es von
NetModel beziehen :
Sie können dies öffnen und das betroffene Netzwerk anzeigen (und ja, wir haben die Anzeige der Netzdiagramme für Version 12.0 aktualisiert):
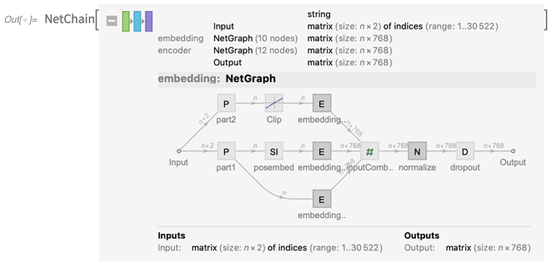
Und Sie können das Netzwerk sofort verwenden, um eine Art "Bedeutungsmerkmale" -Array zu erstellen:
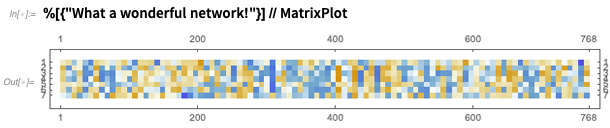
In Version 12.0 haben wir mehrere neue Layertypen eingeführt - insbesondere
AttentionLayer , mit dem die neuesten "Transformator" -Architekturen eingerichtet werden können - und wir haben unsere Funktionen zur "funktionalen Programmierung neuronaler Netze" mit Dingen wie
NetMapThreadOperator und mehreren Sequenzen erweitert
NetFoldOperator . Zusätzlich zu diesen Verbesserungen im
Internet werden in Version 12.0 alle möglichen neuen
NetEncoder- und
NetDecoder- Fälle
hinzugefügt , z. B. die
BPE-Tokenisierung für Text in Hunderten von Sprachen und die Möglichkeit, benutzerdefinierte Funktionen zum Ein- und
Auslesen von
Daten einzuschließen neuronale Netze.
Einige der wichtigsten Verbesserungen in Version 12.0 sind jedoch infrastruktureller.
NetTrain unterstützt jetzt das
Training mit mehreren GPUs sowie den Umgang mit Arithmetik mit gemischter Genauigkeit und flexiblen Kriterien für das frühzeitige Stoppen. Wir verwenden weiterhin das beliebte
MXNet- Low-Level-Framework für neuronale Netze (zu dem wir
maßgeblich beigetragen haben ), damit wir die neuesten Hardwareoptimierungen nutzen können. Es gibt
neue Optionen, um zu sehen, was während des Trainings passiert, und
NetMeasurements , mit denen Sie 33 verschiedene Arten von Messungen zur Leistung eines Netzwerks durchführen können:
Neuronale Netze sind nicht die einzige oder sogar immer die beste Möglichkeit, maschinelles Lernen zu betreiben. Neu in Version 12.0 ist jedoch, dass wir jetzt in der Lage sind, sich
selbst normalisierende Netzwerke automatisch in
Classify and
Predict zu verwenden , sodass sie
neuronale Netze problemlos
nutzen können, wenn dies sinnvoll ist.
Wir haben
ImageIdentify bereits in Version 10.1 eingeführt, um festzustellen, woraus ein Bild besteht. In Version 12.0 ist es uns gelungen, dies zu verallgemeinern, um nicht nur herauszufinden, woraus ein Bild besteht, sondern auch, was in einem Bild enthalten ist. So zeigt
ImageCases beispielsweise Fälle bekannter Arten von Objekten in einem Bild:
Für weitere Details gibt
ImageContents einen Datensatz darüber an, was in einem Bild enthalten ist:
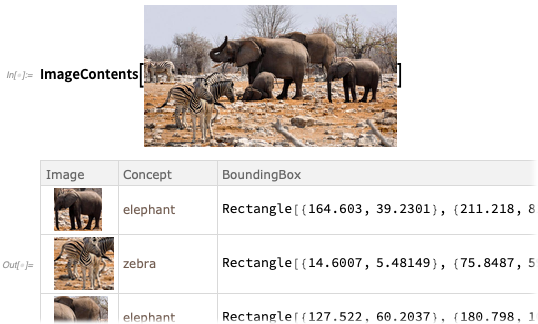
Sie können
ImageCases anweisen , nach einer bestimmten Art von Dingen zu suchen:
Sie können auch einfach testen, ob ein Bild eine bestimmte Art von Dingen enthält:
In gewisser
Weise ist
ImageCases wie eine verallgemeinerte Version von
FindFaces , um menschliche Gesichter in einem Bild zu finden. Neu in Version 12.0 ist, dass
FindFaces und
FacialFeatures effizienter und robuster geworden sind. FindFaces basieren jetzt eher auf neuronalen Netzen als auf klassischer Bildverarbeitung, und das Netzwerk für
FacialFeatures ist jetzt 10 MB statt 500 MB
groß :
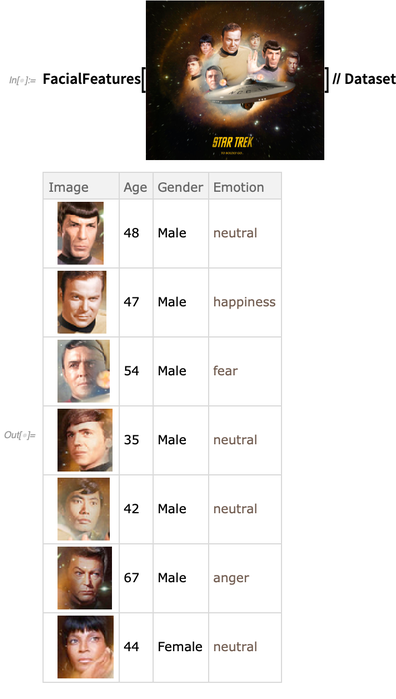
Funktionen wie
ImageCases stellen eine
Bildverarbeitung im „neuen Stil“ dar, wie sie vor einigen Jahren noch nicht denkbar schien. Während solche Funktionen alle möglichen neuen Dinge ermöglichen, sind klassische Techniken immer noch von großem Wert. Wir haben lange Zeit eine ziemlich vollständige
klassische Bildverarbeitung in der Wolfram-Sprache, aber wir nehmen weiterhin inkrementelle Verbesserungen vor.
Ein Beispiel in Version 12.0 ist das
ImagePyramid- Framework für die
mehrskalige Bildverarbeitung:
In Version 12.0 gibt es mehrere neue Funktionen, die sich mit der Farbberechnung befassen. Eine Schlüsselidee ist
ColorsNear , das eine Nachbarschaft im wahrnehmbaren Farbraum darstellt, hier um die Farbe
Pink :
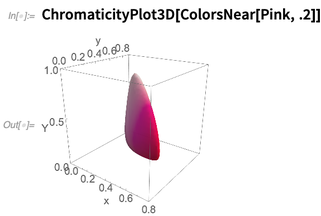
Der Begriff der Farbnachbarschaften kann beispielsweise in der neuen
ImageRecolor- Funktion verwendet werden:
Während ich an meinem Computer sitze und dies schreibe, sage ich etwas zu meinem Computer und nehme
es auf :
Hier ist ein Spektrogramm des von mir aufgenommenen Audios:
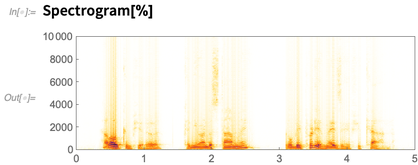
Bisher konnten wir dies in Version 11.3 tun (obwohl
Spectrogram in 12.0 zehnmal schneller wurde). Aber jetzt ist hier etwas Neues:
Wir machen Rede-zu-Text! Wir verwenden modernste neuronale Netztechnologie, aber ich bin erstaunt, wie gut sie funktioniert. Es ist ziemlich rationalisiert und wir sind perfekt in der Lage, auch sehr lange Audiostücke zu verarbeiten, die beispielsweise in Dateien gespeichert sind. Und auf einem typischen Computer läuft die Transkription ungefähr in Echtzeit, so dass eine Stunde Redezeit ungefähr eine Stunde dauert, um sie zu transkribieren.
Im Moment betrachten wir
Speech Recognize als experimentell und werden es weiter verbessern. Es ist jedoch interessant zu sehen, dass eine weitere wichtige Rechenaufgabe in der Wolfram-Sprache zu einer einzigen Funktion wird.
In Version 12.0 gibt es noch weitere Verbesserungen.
SpeechSynthesize unterstützt neue Sprachen und neue Stimmen (wie von
VoiceStyleData [] aufgeführt).
Es gibt jetzt
WebAudioSearch - analog zu
WebImageSearch -, mit dem Sie im Web nach Audio suchen können:
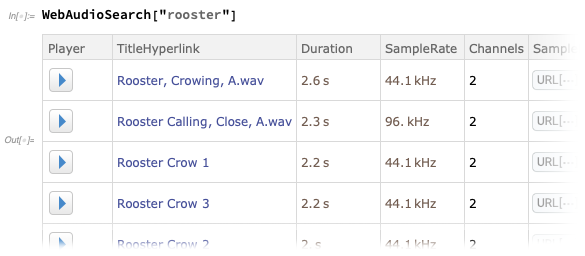
Sie können aktuelle
Audioobjekte abrufen:
Dann können Sie Spektrogramme oder andere Messungen durchführen:
Und dann - neu in Version 12.0 - können Sie mit
AudioIdentify versuchen, die
Klangkategorie zu identifizieren (ist das ein sprechender Hahn?):
Wir betrachten
AudioIdentify weiterhin als experimentell. Es ist ein interessanter Start, aber er funktioniert zum Beispiel definitiv nicht so gut wie
ImageIdentify .
Eine erfolgreichere
Audiofunktion ist
PitchRecognize , die versucht, die dominante Frequenz in einem Audiosignal zu erkennen (es werden sowohl „klassische“ als auch neuronale Netzmethoden verwendet). Es kann noch nicht mit "Akkorden" umgehen, aber es funktioniert ziemlich perfekt für "einzelne Noten".
Wenn man sich mit Audio befasst, möchte man oft nicht nur identifizieren, was im Audio enthalten ist, sondern es auch kommentieren. Mit Version 12.0 wird der Beginn eines umfangreichen
Audio-Frameworks eingeführt . Im
Moment kann
AudioAnnotate markieren, wo Stille herrscht oder wo etwas Lautes ist. In Zukunft werden wir Sprecheridentifikation, Wortgrenzen und vieles mehr hinzufügen. Dazu haben wir auch Funktionen wie
AudioAnnotationLookup , mit denen Sie Teile eines
Audioobjekts auswählen können , die auf bestimmte Weise mit Anmerkungen versehen wurden.
Unter all diesen High-Level-Audiofunktionen befindet sich eine ganze Infrastruktur für die Low-Level-Audioverarbeitung. Version 12.0 verbessert
AudioBlockMap erheblich (zum Anwenden von Filtern auf Audiosignale) und führt Funktionen wie
ShortTimeFourier ein .
Ein Spektrogramm kann ein bisschen wie ein kontinuierliches Analogon einer Partitur betrachtet werden, in der Tonhöhen als Funktion der Zeit aufgetragen sind. In Version 12.0 gibt es jetzt
InverseSpectrogram - das geht von einem Array von Spektrogrammdaten zu Audio. Seit Version 2 im Jahr 1991 haben wir
Play , um Sound aus einer Funktion (wie
Sin [100 t]) zu erzeugen. Mit
Inverse Spectrogram haben wir jetzt die Möglichkeit, von einer „Frequenz-Zeit-Bitmap“ zu einem Sound zu gelangen. (Und ja, es gibt knifflige Probleme mit den besten Vermutungen für Phasen, in denen nur Größeninformationen vorliegen.)
Beginnend mit
Wolfram | Alpha verfügen wir seit langem über außergewöhnlich starke
NLU-Fähigkeiten (Natural Language Understanding) . Und das bedeutet, dass wir bei einem Stück natürlicher Sprache gut darin sind, es als Wolfram-Sprache zu verstehen - aus der wir dann rechnen können:
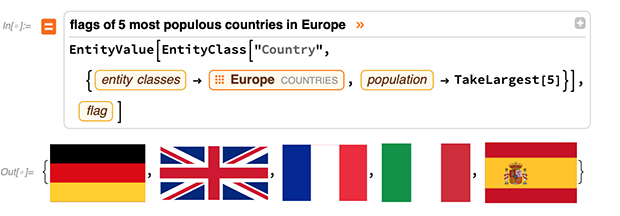
Aber was ist mit der Verarbeitung natürlicher Sprache (NLP)? Wo nehmen wir möglicherweise lange Passagen natürlicher Sprache und versuchen nicht, sie vollständig zu verstehen, sondern nur bestimmte Merkmale zu finden oder zu verarbeiten? Funktionen wie
TextSentences ,
TextStructure ,
TextCases und
WordCounts bieten uns
seit einiger Zeit grundlegende Funktionen in diesem Bereich. In Version 12.0 haben wir uns jedoch durch die Nutzung des neuesten maschinellen Lernens sowie unserer langjährigen NLU- und Knowledgebase-Funktionen zu sehr starken NLP-Funktionen entwickelt.
Das Herzstück ist die dramatisch verbesserte Version von
TextCases . Das grundlegende Ziel von
TextCases ist es, Fälle verschiedener Arten von Inhalten in einem Textstück zu finden. Ein Beispiel hierfür ist die klassische NLP-Aufgabe der „Entitätserkennung“, bei der
TextCases hier herausfinden, welche Ländernamen im
Wikipedia-Artikel über Ozelots erscheinen :
Wir könnten auch fragen, welche Inseln erwähnt werden, aber jetzt werden wir nicht nach einer Interpretation der Wolfram-Sprache fragen:
TextCases ist nicht perfekt, aber es funktioniert ziemlich gut:
Es werden auch viele verschiedene Inhaltstypen unterstützt:
Sie können ihn bitten,
Pronomen oder reduzierte Relativsätze oder
Mengen oder
E-Mail-Adressen oder Vorkommen von 150 Arten von Entitäten (wie
Unternehmen oder
Pflanzen oder
Filmen ) zu finden. Sie können ihn auch bitten, Textteile auszuwählen, die in bestimmten
menschlichen oder
Computersprachen verfasst sind oder sich
auf bestimmte Themen (wie
Reisen oder
Gesundheit ) beziehen oder die eine
positive oder negative Stimmung haben . Und Sie können Konstrukte wie
Containing verwenden , um nach Kombinationen dieser Dinge zu fragen (wie Nominalphrasen, die den Namen eines Flusses enthalten):
Mit TextContents können Sie beispielsweise Details aller Entitäten
anzeigen , die in einem bestimmten Textstück erkannt wurden:
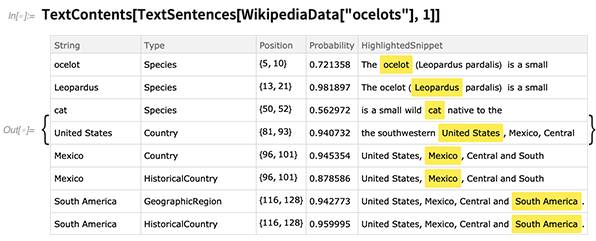
Und ja, man kann diese Funktionen im Prinzip über
FindTextualAnswer nutzen , um Fragen aus dem Text zu beantworten - aber in einem
solchen Fall können die Ergebnisse ziemlich verrückt sein:
Natürlich können Sie eine echte Antwort aus unserer tatsächlich integrierten kuratierten Wissensdatenbank erhalten:
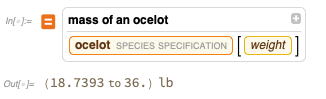
Übrigens haben wir in Version 12.0 eine Reihe kleiner „Funktionen zur Bequemlichkeit natürlicher Sprache“ hinzugefügt, wie
Synonyme und
Antonyme :
Einer der „überraschenden“ neuen Bereiche in Version 12.0 ist die Computerchemie. Wir haben seit langer Zeit Daten zu
explizit bekannten Chemikalien in unserer Wissensdatenbank. In Version 12.0 können wir jedoch mit Molekülen rechnen, die einfach als reine symbolische Objekte angegeben werden. So können wir spezifizieren, was sich als Wassermolekül herausstellt:
Und so können wir ein 3D-Rendering erstellen:
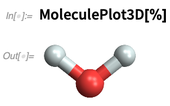
Wir können mit „bekannten Chemikalien“ umgehen:
Wir können beliebige
IUPAC- Namen verwenden:
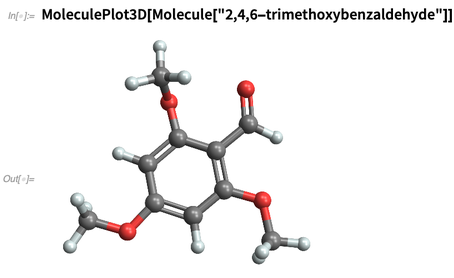
Oder wir „erfinden“ Chemikalien, indem wir sie beispielsweise durch ihre
SMILES- Zeichenfolgen spezifizieren:
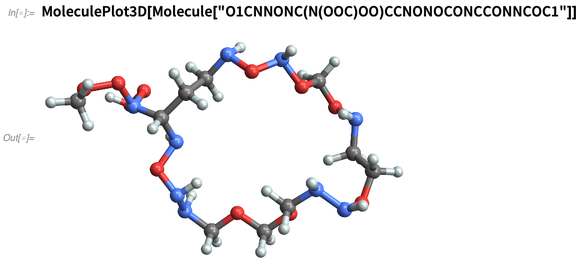
Wir erzeugen hier aber nicht nur Bilder. Wir können auch Dinge aus der Struktur berechnen - wie Symmetrien:
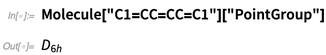
Wenn ein Molekül gegeben ist, können wir beispielsweise Kohlenstoff-Sauerstoff-Bindungen hervorheben:
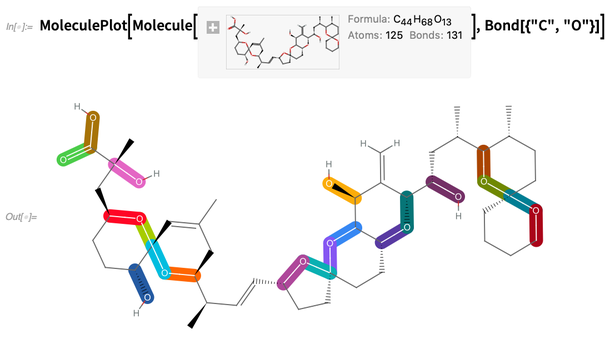
Oder markieren Sie Strukturen, beispielsweise angegeben durch
SMARTS- Zeichenfolgen (hier ein beliebiger 5-
gliedriger Ring):
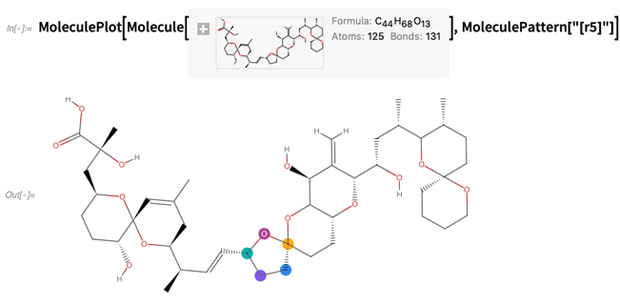
Sie können auch nach „Molekülmustern“ suchen. Die Ergebnisse werden in Form von Atomzahlen angegeben:
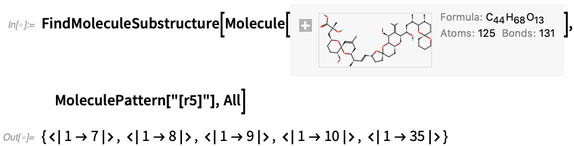
Die Funktionen für Computerchemie, die wir in Version 12.0 hinzugefügt haben, sind ziemlich allgemein und ziemlich leistungsfähig (mit der Einschränkung, dass sie sich bisher nur mit organischen Molekülen befassen). Auf der untersten Ebene betrachten sie Moleküle als markierte Graphen mit Kanten, die Bindungen entsprechen. Sie kennen sich aber auch mit Physik aus und berücksichtigen atomare Valenzen und Bindungskonfigurationen korrekt. Es ist unnötig zu erwähnen, dass es viele Details gibt (über Stereochemie, Symmetrie, Aromatizität, Isotope usw.). Das Endergebnis ist jedoch, dass die molekulare Struktur und die molekulare Berechnung nun erfolgreich in die Liste der Bereiche aufgenommen wurden, die in die Wolfram-Sprache integriert sind.
Die Wolfram-Sprache verfügt bereits über starke Funktionen für das geografische Rechnen, aber Version 12.0 fügt weitere Funktionen hinzu und erweitert einige der bereits vorhandenen.
Zum Beispiel gibt es jetzt
RandomGeoPosition , die eine zufällige lat-lange Position generiert. Man könnte denken, dass dies trivial wäre, aber natürlich muss man sich um Koordinatentransformationen sorgen - und was es viel trivialer macht, ist, dass man ihm sagen kann, dass er nur innerhalb einer bestimmten Region, hier des Landes Frankreich, Punkte auswählen soll:
Ein Thema der neuen geografischen Funktionen in Version 12.0 ist die Behandlung nicht nur geografischer Punkte und Regionen, sondern auch geografischer Vektoren. Hier ist der aktuelle Windvektor zum Beispiel an der Position des Eiffelturms, dargestellt als
GeoVector , mit Geschwindigkeit und Richtung (es gibt auch
GeoVectorENU , das Ost-, Nord- und Aufwärtskomponenten sowie
GeoGridVector und
GeoVectorXYZ enthält ):
Mit Funktionen wie
GeoGraphics können Sie diskrete
Geovektoren visualisieren.
GeoStreamPlot ist das Geo-Analogon von
StreamPlot (oder
ListStreamPlot ) und zeigt Stromlinien, die aus
Geovektoren (hier aus
WindDirectionData ) gebildet wurden:
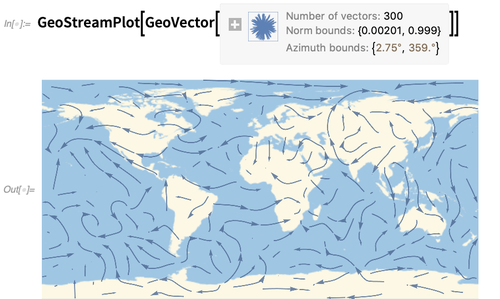
Geodäsie ist ein mathematisch anspruchsvolles Gebiet, und wir sind stolz darauf, es in der Wolfram-Sprache gut zu machen. In Version 12.0 haben wir einige neue Funktionen hinzugefügt, um einige Details zu ergänzen. Zum Beispiel haben wir jetzt Funktionen wie
GeoGridUnitDistance und
GeoGridUnitArea, die die Verzerrung (im Grunde Eigenwerte des Jacobi)
angeben , die mit verschiedenen Geoprojektionen an jeder Position auf der Erde (oder Mond, Mars usw.) verbunden ist.
Eine Richtung der Visualisierung, die wir ständig weiterentwickelt haben, ist das, was man als „Metagrafiken“ bezeichnen könnte: das Beschriften und Kommentieren grafischer Dinge. Wir haben
Callout in Version 11.0 eingeführt. In Version 12.0 wurde es auf Dinge wie 3D-Grafiken erweitert:
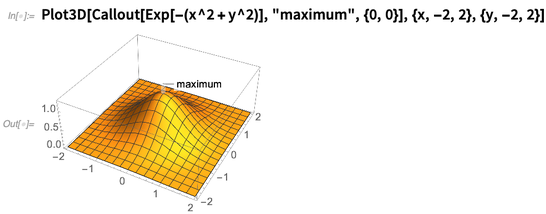
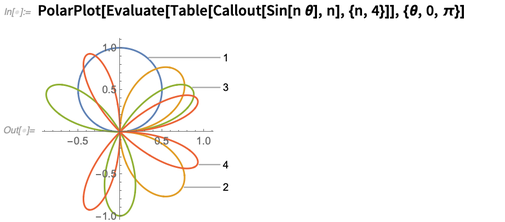
Es ist ziemlich gut herauszufinden, wo Dinge zu beschriften sind, auch wenn sie etwas komplex werden:
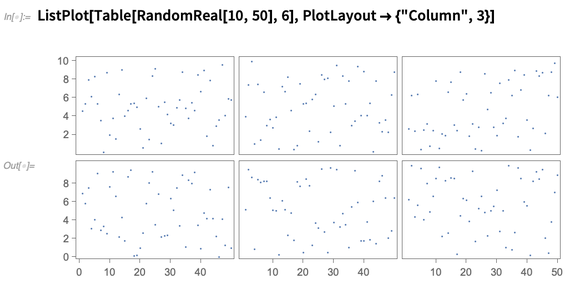
Es gibt viele Details, die wichtig sind, damit Grafiken wirklich gut aussehen. In Version 12.0 wurde verbessert, dass Grafikspalten unabhängig von der Länge der Tick-Beschriftungen in ihren Frames ausgerichtet sind. Wir haben auch
LabelVisibility hinzugefügt, mit dem Sie die relativen Prioritäten festlegen können, mit denen verschiedene Beschriftungen sichtbar gemacht werden sollen.
Eine weitere neue Funktion von Version 12.0 ist das Multipanel-Plot-Layout, bei dem verschiedene Datensätze in verschiedenen Bedienfeldern angezeigt werden. Die Bedienfelder teilen sich jedoch Achsen, wann immer sie können:
Verbesserung der Integration der Wissensdatenbank
Unsere kuratierte Wissensdatenbank, die beispielsweise
Wolfram | Alpha antreibt, ist riesig und wächst kontinuierlich. Und mit jeder Version der Wolfram-Sprache verstärken wir schrittweise ihre Integration in den Kern der Sprache.
In Version 12.0 besteht eine Sache darin, Hunderte von Entitätstypen direkt in der Sprache verfügbar zu machen:
Vor Version 12.0 dienten die
Wolfram | Alpha-Beispielseiten als Proxy für die Dokumentation vieler Arten von Entitäten. Aber jetzt gibt es für alle eine Wolfram Language-Dokumentation:
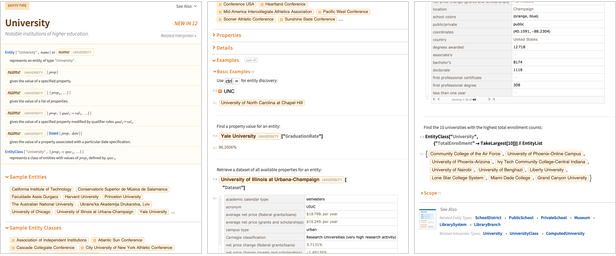
Es gibt immer noch Funktionen wie
SatelliteData ,
WeatherData und
FinancialData , die Entitätstypen verarbeiten, die routinemäßig eine komplexe Auswahl oder Berechnung erfordern. In Version 12.0 kann jedoch auf jeden Entitätstyp auf dieselbe Weise zugegriffen werden, mit Eingaben in
natürlicher Sprache („Steuerelement + =“) und Entitäten und Eigenschaften mit gelbem Kästchen:
Übrigens kann man auch implizit Entitäten verwenden, wie hier nach den 5 Elementen mit den höchsten bekannten Schmelzpunkten fragen:
Und man kann
Dated verwenden , um eine Zeitreihe von Werten zu erhalten:
Wir haben es sehr bequem gemacht, mit Daten zu arbeiten, die in die
Wolfram Knowledgebase integriert sind . Sie haben Entitäten, und es ist sehr einfach, nach Eigenschaften usw. zu fragen:
Aber was ist, wenn Sie Ihre eigenen Daten haben? Können Sie es so einrichten, dass Sie es so einfach verwenden können? Eine
wichtige Neuerung in Version 11 war das Hinzufügen von
EntityStore , in dem man
eigene Entitätstypen definieren und dann Entitäten, Eigenschaften und Werte angeben kann.
Das
Wolfram Data Repository enthält eine
Reihe von Beispielen für Entitätsspeicher . Hier ist einer:
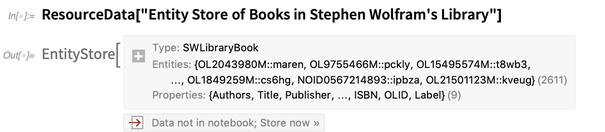
Es beschreibt einen einzelnen Entitätstyp: ein
"SWLibraryBook" . Um Entitäten dieses Typs genau wie integrierte Entitäten verwenden zu können, "registrieren" wir den Entitätsspeicher:
Jetzt können wir beispielsweise nach 10 zufälligen Entitäten vom Typ
"SWLibraryBook" fragen :
Jede Entität im Entitätsspeicher verfügt über verschiedene Eigenschaften. Hier ist ein Datensatz mit den Werten von Eigenschaften für eine bestimmte Entität:
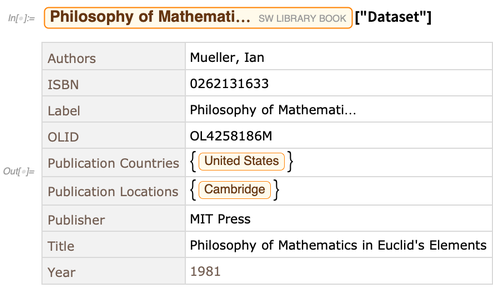
OK, aber mit diesem Setup lesen wir im Grunde den gesamten Inhalt eines Entitätsspeichers in den Speicher. Dies macht es sehr effizient, alle gewünschten Wolfram-Sprachoperationen durchzuführen. Es ist jedoch keine gute skalierbare Lösung für große Datenmengen - zum Beispiel Daten, die zu groß sind, um in den Speicher zu passen.
Aber was ist eine typische Quelle für große Datenmengen? Sehr oft handelt es sich um eine Datenbank und normalerweise um eine relationale Datenbank, auf die über
SQL zugegriffen werden kann. Wir haben unser
DatabaseLink-Paket für Lese- und Schreibzugriff auf SQL-Datenbanken auf niedriger Ebene seit mehr als einem Jahrzehnt. In Version 12.0 fügen wir jedoch einige wichtige integrierte Funktionen hinzu, mit denen externe relationale Datenbanken in der Wolfram-Sprache genauso behandelt werden können wie Entity Stores oder integrierte Teile der Wolfram Knowledgebase.
Beginnen wir mit einem Spielzeugbeispiel. Hier ist eine symbolische Darstellung einer kleinen relationalen Datenbank, die zufällig in einer Datei gespeichert ist:
Sofort erhalten wir eine Box, die zusammenfasst, was sich in der Datenbank befindet, und uns mitteilt, dass diese Datenbank 8 Tabellen enthält. Wenn wir die Box öffnen, können wir mit der Überprüfung der Struktur dieser Tabellen beginnen:
Wir können diese relationale Datenbank dann als Entitätsspeicher in der Wolfram-Sprache einrichten. Es sieht sehr ähnlich aus wie der oben genannte Bibliotheksbuch-Entitätsspeicher, aber jetzt werden die tatsächlichen Daten nicht in den Speicher gezogen. Stattdessen befindet es sich immer noch in der externen relationalen Datenbank, und wir definieren lediglich eine ("ORM-ähnliche") Zuordnung zu Entitäten in der Wolfram-Sprache:
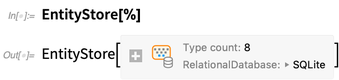
Jetzt können wir diesen Entitätsspeicher registrieren, der eine Reihe von Entitätstypen einrichtet, die (zumindest standardmäßig) nach den Namen der Tabellen in der Datenbank benannt sind:
Und jetzt können wir "Entitätsberechnungen" für diese durchführen, genau wie für integrierte Entitäten in der Wolfram Knowledgebase. Jede Entität entspricht hier einer Zeile in der Tabelle "Mitarbeiter" in der Datenbank:
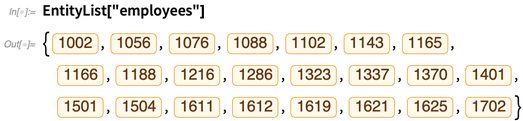
Für einen bestimmten Entitätstyp können wir fragen, welche Eigenschaften er hat. Diese "Eigenschaften" entsprechen Spalten in der Tabelle in der zugrunde liegenden Datenbank:
Jetzt können wir nach dem Wert einer bestimmten Eigenschaft einer bestimmten Entität fragen:
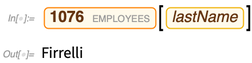
Wir können Entitäten auch anhand von Kriterien auswählen. Hier fragen wir nach "Zahlungs" -Entitäten mit den 4 größten Werten der "Betrag" -Eigenschaft:
Wir können gleichermaßen nach den Werten dieser größten Beträge fragen:
OK, aber hier wird es interessanter: Bisher haben wir uns eine kleine dateibasierte Datenbank angesehen. Mit einer riesigen Datenbank, die auf einem externen Server gehostet wird, können wir genau das Gleiche tun.
Stellen Sie als Beispiel eine Verbindung zur
OpenStreetMap PostgreSQL-Datenbank in Terabyte-Größe her, die im Grunde die Straßenkarte der Welt enthält:
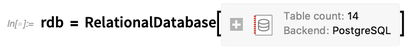
Registrieren wir nach wie vor die Tabellen in dieser Datenbank als Entitätstypen. Wie bei den meisten In-the-Wild-Datenbanken gibt es kleine Störungen in der Struktur, die umgangen werden, aber Warnungen generieren:
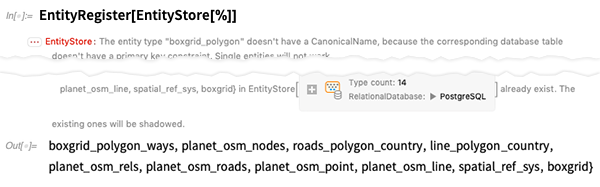
Aber jetzt können wir Fragen zur Datenbank stellen - wie viele Geopunkte oder „Knoten“ es auf allen Straßen der Welt gibt (und ja, es ist eine große Zahl, weshalb die Datenbank groß ist):
Hier fragen wir nach den Namen der Objekte mit den 10 größten (projizierten) Bereichen in der Tabelle (101 GB) planet_osm_polygon (und ja, es dauert weniger als eine Sekunde):
Wie funktioniert das alles? Grundsätzlich geschieht, dass unsere Wolfram Language-Darstellung in SQL-Abfragen auf niedriger Ebene kompiliert wird, die dann gesendet werden, um direkt auf dem Datenbankserver ausgeführt zu werden.
Manchmal werden Sie nach Ergebnissen fragen, die nur Endwerte sind (wie zum Beispiel die oben genannten „Beträge“). In anderen Fällen möchten Sie jedoch etwas Zwischenprodukt - wie eine Sammlung von Entitäten, die auf eine bestimmte Weise ausgewählt wurden. Und natürlich könnte diese Sammlung eine Milliarde Einträge haben. Ein sehr wichtiges Merkmal der Einführung in Version 12.0 ist daher, dass wir solche Dinge rein symbolisch darstellen und manipulieren können und sie erst am Ende in etwas Bestimmtes auflösen können.
Zurück zu unserer Spielzeugdatenbank: Hier ein Beispiel, wie wir eine Klasse von Entitäten angeben, die durch Aggregation des gesamten
creditLimit für alle
Kunden mit einem bestimmten Wert des
Landes erhalten werden :
Das ist zunächst nur etwas Symbolisches. Wenn wir jedoch nach bestimmten Werten fragen, werden die tatsächlichen Datenbankabfragen durchgeführt und wir erhalten bestimmte Ergebnisse:
Es gibt eine Reihe neuer Funktionen zum Einrichten verschiedener Arten von Abfragen. Die Funktionen funktionieren nicht nur für relationale Datenbanken, sondern auch für Entitätsspeicher und für die integrierte Wolfram Knowledgebase. So können wir beispielsweise im
Periodensystem der Elemente nach der durchschnittlichen Atommasse für einen bestimmten Zeitraum fragen:
Ein wichtiges neues Konstrukt ist
EntityFunction .
EntityFunction ähnelt
Function , mit der Ausnahme, dass seine Variablen Entitäten (oder
Entitätsklassen ) darstellen und Vorgänge beschreiben, die direkt in externen Datenbanken ausgeführt werden können. Hier ist ein Beispiel mit integrierten Daten, in dem wir eine "gefilterte" Entitätsklasse definieren, in der das Filterkriterium eine Funktion ist, die Populationswerte testet. Die
FilteredEntityClass selbst wird nur symbolisch dargestellt, aber
EntityList führt die Abfrage tatsächlich aus und löst eine explizite Liste von (hier unsortierten) Entitäten auf:
Zusätzlich zu
EntityFunction ,
AggregatedEntityClass und
SortedEntityClass enthält Version 12.0
SampledEntityClass (um einige Entitäten aus einer Klasse
abzurufen ),
ExtendedEntityClass (um berechnete Eigenschaften hinzuzufügen) und
CombinedEntityClass (um Eigenschaften aus verschiedenen Klassen zu kombinieren). Mit diesen Grundelementen kann man alle Standardoperationen der „
relationalen Algebra “ aufbauen.
Bei der Standard-Datenbankprogrammierung endet man normalerweise mit einem ganzen Dschungel von "Joins" und "Fremdschlüsseln" und so weiter. Mit unserer Wolfram Language-Darstellung können Sie auf einer höheren Ebene arbeiten - wobei Verknüpfungen im Grunde genommen zur Funktionszusammensetzung werden und Fremdschlüssel nur unterschiedliche Entitätstypen sind. (Wenn Sie jedoch explizite Verknüpfungen durchführen möchten, können Sie dies beispielsweise mit
CombinedEntityClass tun.)
Unter der Haube geht es darum, dass all diese Wolfram Language-Konstrukte in SQL kompiliert werden, genauer gesagt in den spezifischen
SQL- Dialekt, der für die von Ihnen verwendete Datenbank geeignet ist (wir unterstützen derzeit
SQLite ,
MySQL ,
PostgreSQL und
MS) -SQL , mit Unterstützung für
OracleSQL in Kürze). Wenn wir die Kompilierung durchführen, überprüfen wir automatisch die Typen, um sicherzustellen, dass Sie eine aussagekräftige Abfrage erhalten. Selbst relativ einfache Wolfram-Sprachspezifikationen können sich in viele SQL-Zeilen verwandeln. Zum Beispiel
würde das folgende Zwischen-SQL erzeugen (hier zum Abfragen der SQLite-Datenbank):
Das Datenbankintegrationssystem in Version 12.0 ist ziemlich ausgefeilt - und wir arbeiten seit einigen Jahren daran. Dies ist ein wichtiger Schritt vorwärts, damit die Wolfram-Sprache direkt mit einem neuen Grad an „Größe“ in Big Data umgehen kann - und die Wolfram-Sprache direkt Datenwissenschaft für Datensätze mit Terabyte-Größe und darüber hinaus durchführen kann. Als würde man herausfinden, welche straßenähnlichen Wesen auf der Welt „Wolfram“ in ihrem Namen haben:
Was ist der beste Weg, um Wissen über die Welt darzustellen? Es ist ein Thema, das seit der Antike von Philosophen (und anderen) diskutiert wurde. Manchmal sagten die Leute, Logik sei der Schlüssel. Manchmal Mathematik. Manchmal relationale Datenbanken. Aber jetzt kennen wir mindestens eine solide Grundlage (oder zumindest bin ich mir ziemlich sicher): Alles kann durch Berechnung dargestellt werden. Dies ist eine überzeugende Idee - und in gewissem Sinne macht dies alles möglich, was wir mit Wolfram Language tun.
Aber gibt es Teilmengen allgemeiner Berechnungen, die nützlich sind, um zumindest bestimmte Arten von Wissen darzustellen? Eine, die wir in der
Wolfram Knowledgebase häufig verwenden, ist der Begriff der Entitäten ("New York City"), Immobilien ("Bevölkerung") und ihrer Werte ("8,6 Millionen Menschen"). Natürlich repräsentieren solche Tripel nicht alles Wissen in der Welt („Wie wird die Position des Mars morgen sein?“). Aber sie sind ein guter Anfang, wenn es um bestimmte Arten von „statischem“ Wissen über bestimmte Dinge geht.
Wie kann man diese Art der Wissensrepräsentation formalisieren? Eine Antwort sind Graphendatenbanken. Und in Version 12.0 unterstützen wir - in Übereinstimmung mit vielen
„Semantic Web“ -Projekten - Graphendatenbanken mit
RDF und Abfragen mit
SPARQL . In RDF ist das zentrale Objekt eine
IRI („Internationalized Resource Identifier“), die eine Entität oder eine Eigenschaft darstellen kann. Ein "
Triplestore " besteht dann aus einer Sammlung von Tripeln ("Subjekt", "Prädikat", "Objekt"), wobei jedes Element in jedem Tripel ein IRI (oder ein Literal wie eine Zahl) ist. Das gesamte Objekt kann dann als Graphendatenbank oder Graphspeicher oder mathematisch als Hypergraph betrachtet werden. (Es ist ein
Hypergraph, da das Prädikat "Kanten" auch an anderer Stelle Scheitelpunkte sein kann.)
Sie können Ihren eigenen
RDFStore ähnlich wie einen
EntityStore erstellen - und tatsächlich können Sie jeden Wolfram Language
EntityStore mit SPARQL abfragen, genau wie Sie einen
RDFStore abfragen. Und da der Entity-Property-Teil der Wolfram Knowledgebase als Entity-Store behandelt werden kann, können Sie dies auch abfragen. Hier ist also endlich ein Beispiel. Die Länder-Stadt-Liste
Entität ["
Land "],
Entität ["
Stadt "]} repräsentiert tatsächlich einen RDF-Speicher. Dann ist
SPARQLSelect ein Operator, der auf diesen Speicher einwirkt. Es wird versucht, ein Tripel zu finden, das Ihren Anforderungen entspricht, mit einem bestimmten Wert für die „SPARQL-Variable“ x:
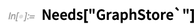
Natürlich gibt es auch einen viel einfacheren Weg, dies in der Wolfram-Sprache zu tun:
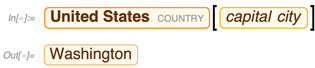
Aber mit SPARQL können Sie viel exotischere Dinge tun - wie fragen, welche Eigenschaften die USA mit Mexiko in Verbindung bringen:
Oder ob es einen Weg gibt, der auf der Beziehung der angrenzenden Länder von Portugal nach Deutschland basiert:
Im Prinzip können Sie eine SPARQL-Abfrage einfach als Zeichenfolge schreiben (ähnlich wie Sie eine SQL-Zeichenfolge schreiben können). In Version 12.0 haben wir jedoch eine symbolische Darstellung von SPARQL eingeführt, die die Berechnung der Darstellung selbst ermöglicht und es beispielsweise einfach macht, komplexe SPARQL-Abfragen automatisch zu generieren. (Und dies ist besonders wichtig, da praktische SPARQL-Abfragen für sich genommen die Gewohnheit haben, extrem lang und schwerfällig zu werden.)
OK, aber gibt es RDF-Läden in freier Wildbahn? Es war eine langjährige Hoffnung, dass ein großer Teil des Webs irgendwie genug markiert wird, um „semantisch“ zu werden und tatsächlich ein riesiger RDF-Laden zu sein. Es wäre großartig, wenn dies passieren würde, aber bisher definitiv nicht. Trotzdem gibt es einige öffentliche RDF-Stores und auch einige RDF-Stores innerhalb von Organisationen. Mit unseren neuen Funktionen in Version 12.0 sind wir in der einzigartigen Position, interessante Dinge mit ihnen zu tun.
Eine unglaublich häufige Form von Problemen in industriellen Anwendungen der Mathematik ist: „Welche Konfiguration minimiert die Kosten (oder maximiert die Auszahlung), wenn bestimmte Einschränkungen erfüllt werden müssen?“ Vor mehr als einem halben Jahrhundert wurde der sogenannte
Simplex-Algorithmus zur Lösung linearer Versionen dieser Art von Problem erfunden, bei denen sowohl die Zielfunktion (Kosten, Auszahlung) als auch die Einschränkungen lineare Funktionen der Variablen im Problem sind. In den 1980er Jahren wurden viel effizientere Methoden („innere Punkte“) erfunden - und diese hatten wir schon lange für die „
lineare Programmierung “ in der Wolfram-Sprache.
Aber was ist mit nichtlinearen Problemen? Nun, im allgemeinen Fall kann man Funktionen wie NMinimize verwenden. Und sie machen einen hochmodernen Job. Aber es ist ein schweres Problem. Vor einigen Jahren wurde jedoch klar, dass es selbst unter nichtlinearen Optimierungsproblemen eine Klasse von sogenannten konvexen Optimierungsproblemen gibt, die tatsächlich fast so effizient gelöst werden können wie lineare. ("Konvex" bedeutet, dass sowohl das Ziel als auch die Einschränkungen nur konvexe Funktionen beinhalten - so dass nichts "wackeln" kann, wenn man sich einem Extrem nähert, und es kann keine lokalen Minima geben, die keine globalen Minima sind.)
In Version 12.0 haben wir jetzt starke Implementierungen für alle verschiedenen Standardklassen der konvexen Optimierung. Hier ist ein einfacher Fall, bei dem eine quadratische Form mit einigen linearen Einschränkungen minimiert wird:
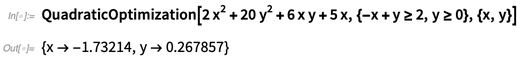NMinimize konnte dieses spezielle Problem bereits in Version 11.3 lösen:
Aber wenn man mehr Variablen hätte, würde die alte
NMinimize schnell ins
Stocken geraten . In Version 12.0 funktioniert die
quadratische Optimierung jedoch weiterhin einwandfrei, bis zu mehr als 100.000 Variablen mit mehr als 100.000 Einschränkungen (sofern sie recht spärlich sind).
In Version 12.0 haben wir Funktionen zur „rohen konvexen Optimierung“ wie
SemidefiniteOptimization (die lineare Matrixungleichungen behandelt) und
ConicOptimization (die lineare
Vektorungleichungen behandelt). Funktionen wie
NMinimize und
FindMinimum erkennen jedoch auch automatisch, wann ein Problem effizient gelöst werden kann, indem sie in eine konvexe Optimierungsform umgewandelt werden.
Wie richtet man konvexe Optimierungsprobleme ein? Größere beinhalten Einschränkungen für ganze Vektoren oder Matrizen von Variablen. Und in Version 12.0 haben wir jetzt Funktionen wie
VectorGreaterEqual (Eingabe als ≥), die diese sofort darstellen können.
Partielle Differentialgleichungen sind schwierig, und wir arbeiten seit 30 Jahren an immer ausgefeilteren und allgemeineren Methoden, um damit umzugehen. Wir haben
NDSolve (für ODEs)
bereits 1991 in
Version 2 eingeführt . Mitte der neunziger Jahre hatten wir unsere ersten (1 + 1-dimensionalen) numerischen PDEs. 2003 haben wir unser leistungsstarkes, modulares Framework für den Umgang mit numerischen Differentialgleichungen eingeführt. In Bezug auf PDEs handelte es sich jedoch im Grunde immer noch nur um einfache rechteckige Regionen. Um darüber hinauszugehen, musste unser gesamtes
rechnergestütztes Geometriesystem erstellt werden , das wir in Version 10 eingeführt haben. Damit haben wir
unsere ersten Finite-Elemente-PDE-Löser veröffentlicht . In Version 11 haben wir dann auf
Eigenprobleme verallgemeinert.
In Version 12 führen wir nun eine weitere wichtige Verallgemeinerung ein: die nichtlineare Finite-Elemente-Analyse. Bei der Finite-Elemente-Analyse werden Bereiche in kleine diskrete Dreiecke, Tetraeder usw. zerlegt, auf denen die ursprüngliche PDE durch eine große Anzahl gekoppelter Gleichungen angenähert werden kann. Wenn die ursprüngliche PDE linear ist, sind diese Gleichungen auch linear - und das ist der typische Fall, den Menschen berücksichtigen, wenn sie über „Finite-Elemente-Analyse“ sprechen.
Es gibt jedoch viele PDEs von praktischer Bedeutung, die nicht linear sind - und um diese zu lösen, ist eine nichtlineare Finite-Elemente-Analyse erforderlich, wie wir sie jetzt in Version 12.0 haben.
Als Beispiel ist hier das, was nötig ist, um die böse nichtlineare PDE zu lösen, die die Höhe einer minimalen 2D-Oberfläche (z. B. eines idealisierten Seifenfilms) hier über einem Ring mit (Dirichlet-) Randbedingungen beschreibt, die dazu führen, dass sie sinusförmig an der wackelt Kanten (als ob der Seifenfilm an Drähten aufgehängt wäre):
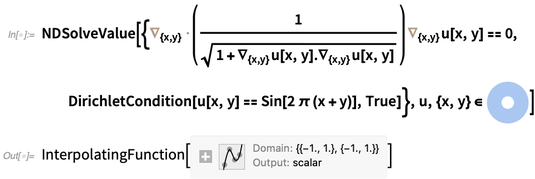
Auf meinem Computer dauert es nur eine Viertelsekunde, um diese Gleichung zu lösen und eine Interpolationsfunktion zu erhalten. Hier ist eine grafische Darstellung der Interpolationsfunktion, die die Lösung darstellt:
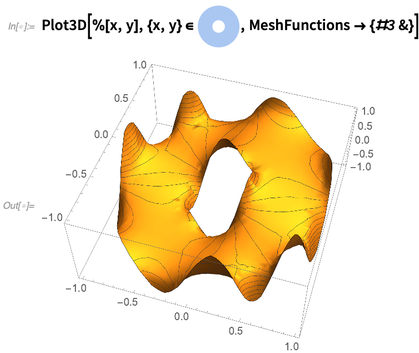
Wir haben im Laufe der Jahre viel Technik in die Optimierung der Ausführung von Wolfram Language-Programmen gesteckt. Bereits 1989 haben wir begonnen, einfache numerische Berechnungen mit Maschinengenauigkeit automatisch zu Anweisungen für eine effiziente virtuelle Maschine zu kompilieren (und zufällig habe ich den Originalcode dafür geschrieben). Im Laufe der Jahre haben wir die Funktionen dieses Compilers erweitert, aber es war immer auf ziemlich einfache Programme beschränkt.
In Version 12.0 machen wir einen großen Schritt nach vorne und veröffentlichen die erste Version eines neuen, viel leistungsfähigeren Compilers, an dem wir seit mehreren Jahren arbeiten. Dieser Compiler kann sowohl eine viel breitere Palette von Programmen (einschließlich komplexer Funktionskonstrukte und aufwändiger Kontrollabläufe) verarbeiten als auch nicht auf einer virtuellen Maschine kompilieren, sondern direkt auf optimierten nativen Maschinencode.
In Version 12.0 betrachten wir den neuen Compiler immer noch als experimentell. Aber es schreitet schnell voran und wird sich dramatisch auf die Effizienz vieler Dinge in der Wolfram-Sprache auswirken. In Version 12.0 stellen wir lediglich eine „Kit-Form“ des neuen Compilers mit spezifischen Kompilierungsfunktionen zur Verfügung. Aber wir werden den Compiler nach und nach immer automatischer arbeiten lassen - mit maschinellem Lernen und anderen Methoden herausfinden, wann es sich lohnt, sich die Zeit zu nehmen, um welche Kompilierungsstufe zu erreichen.
Auf technischer Ebene basiert der neue Compiler der Version 12.0 auf LLVM und generiert LLVM-Code. Er verknüpft dieselbe Laufzeitbibliothek auf niedriger Ebene, die der Wolfram Language-Kernel selbst verwendet, und ruft für die Funktionalität den vollständigen Wolfram Language-Kernel auf das ist nicht in der Laufzeitbibliothek.
Hier ist die grundlegende Art und Weise, wie eine reine Funktion in der aktuellen Version des neuen Compilers kompiliert wird:
Die resultierende kompilierte Codefunktion funktioniert genauso wie die ursprüngliche Funktion, ist jedoch schneller:
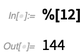
Ein großer Teil dessen, was
FunctionCompile zu einer schnelleren Funktion macht, besteht darin, dass Sie ihm sagen, dass er Annahmen über die Art des Arguments treffen soll, das er erhalten wird. Wir unterstützen viele Grundtypen (wie "
Integer32 " und "
Real64 "). Wenn Sie jedoch
FunctionCompile verwenden , legen Sie bestimmte Argumenttypen fest, sodass viel optimierterer Code erstellt werden kann.
Ein Großteil der Raffinesse des neuen Compilers hängt damit zusammen, welche Datentypen bei der Ausführung eines Programms generiert werden. (Es gibt viele graphentheoretische und andere Algorithmen, und natürlich erfolgt die gesamte Metaprogrammierung für den Compiler mit der Wolfram-Sprache.)
Hier ist ein Beispiel, das ein bisschen Typinferenz beinhaltet (der Typ von
fib wird abgeleitet als
"Integer64" -> "Integer64" : eine Ganzzahlfunktion, die eine Ganzzahl
zurückgibt ):
Auf meinem Computer läuft
cf [25] ungefähr 300-mal schneller als die nicht kompilierte Funktion. (Natürlich schlägt die kompilierte Version fehl, wenn ihre Ausgabe nicht mehr vom Typ "
Integer64 " ist, aber die Standardversion von Wolfram Language funktioniert weiterhin
einwandfrei .)
Der Compiler kann bereits Hunderte von Wolfram Language-Programmierprimitiven verarbeiten, die erzeugten Typen entsprechend verfolgen und Code generieren, der diese Primitive direkt implementiert. Manchmal möchte man jedoch ausgefeilte Funktionen in der Wolfram-Sprache verwenden, für die es keinen Sinn macht, eigenen kompilierten Code zu generieren - und wo man wirklich nur den Wolfram-Language-Kernel für diese Funktionen aufrufen möchte . In Version 12.0 können Sie mit
KernelFunction Folgendes tun:
OK, aber sagen wir, man hat eine kompilierte Codefunktion. Was kann man damit machen? Zunächst einmal kann man es einfach in der Wolfram-Sprache ausführen. Man kann es auch speichern und später ausführen. Eine bestimmte Kompilierung wird für eine bestimmte Prozessorarchitektur (z. B. 64-Bit x86) durchgeführt.
CompiledCodeFunction speichert jedoch automatisch genügend Informationen, um bei Bedarf eine zusätzliche Kompilierung für eine andere Architektur durchzuführen.
Bei einer
CompiledCodeFunction besteht eine der interessanten neuen Möglichkeiten darin, dass direkt Code generiert werden kann, der auch außerhalb der Wolfram Language-Umgebung ausgeführt werden kann. (Unser alter Compiler hatte das
CCodeGenerate- Paket, das in einfachen Fällen etwas ähnliche Funktionen bot - obwohl es selbst dann auf einer ausgeklügelten Toolchain von C-Compilern usw. beruht.)
So kann man rohen LLVM-Code exportieren (beachten Sie, dass Dinge wie die Optimierung der Schwanzrekursion automatisch ausgeführt werden - und beachten Sie am Ende auch die symbolische Funktion und die Compileroptionen):
Wenn man
FunctionCompileExportLibrary verwendet , erhält man eine Bibliotheksdatei - .dylib unter Mac, .dll unter Windows und .so unter Linux. Sie können dies in der Wolfram-Sprache verwenden, indem Sie
LibraryFunctionLoad ausführen . Man kann es aber auch in einem externen Programm verwenden.
Eines der wichtigsten Dinge, die die Allgemeinheit des neuen Compilers bestimmen, ist der Reichtum seines Typsystems.
Derzeit unterstützt der Compiler
14 Atomtypen (wie "
Boolean ", "
Integer8 ", "
Complex64 " usw.). Es werden auch
Typkonstruktoren wie "
PackedArray " unterstützt,
sodass beispielsweise
TypeSpecifier ["
PackedArray "] [
"Real64", 2 ] einem gepackten Array von 64-Bit-Reals mit Rang 2 entspricht.
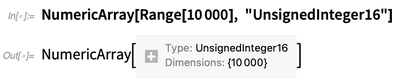
Bei der internen Implementierung der Wolfram-Sprache (die übrigens selbst hauptsächlich in Wolfram-Sprache vorliegt) hatten wir lange Zeit eine optimierte Möglichkeit, Arrays zu speichern. In Version 12.0 wird es als
NumericArray verfügbar gemacht . Im Gegensatz zu normalen Wolfram Language-Konstrukten müssen Sie
NumericArray detailliert mitteilen, wie Daten gespeichert werden sollen. Aber dann funktioniert es auf eine schöne, optimierte Weise:
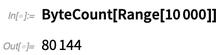
In Version 11.2 haben wir
ExternalEvaluate eingeführt, mit dem Sie Berechnungen in Sprachen wie
Python und
JavaScript aus der Wolfram-Sprache heraus durchführen können (in
Python bedeutet „^“
BitXor ):
In Version 11.3 haben wir externe Sprachzellen eingeführt, um die Eingabe von externen Sprachprogrammen oder anderen Eingaben direkt in ein Notizbuch zu vereinfachen:
In Version 12.0 verschärfen wir die Integration. In einer externen Sprachzeichenfolge können Sie beispielsweise <* ... *> verwenden, um Wolfram Language-Code zur Auswertung zu geben:
Dies funktioniert auch in externen Sprachzellen:
Natürlich ist Python keine Wolfram-Sprache, so viele Dinge funktionieren nicht:
ExternalEvaluate kann jedoch zumindest viele Datentypen aus Python zurückgeben, einschließlich Listen (als
Liste ), Wörterbücher (als
Zuordnung ), Bilder (als
Bild ), Datumsangaben (als
DateObject ),
NumPy-Arrays (als
NumericArray ) und
Pandas-Datasets (als
TimeSeries) ,
DataSet usw.). (
ExternalEvaluate kann auch
ExternalObject zurückgeben , das im Grunde ein Handle für ein Objekt ist, das Sie an Python zurücksenden können.)
Sie können auch externe Funktionen direkt verwenden (das leicht bizarr benannte Ord ist im Grunde das Python-Analogon von
ToCharacterCode ):
Und hier ist eine reine Python-Funktion, die symbolisch in der Wolfram-Sprache dargestellt wird:
Aufrufen der Wolfram-Sprache von Python und anderen Orten aus
Wie soll man auf die Wolfram-Sprache zugreifen? Es gibt viele Möglichkeiten. Man kann es direkt in einem Notebook verwenden. Man kann
APIs aufrufen , die es in der Cloud ausführen. Oder man kann
WolframScript in einer
Befehlszeilen-Shell verwenden . WolframScript kann entweder gegen eine lokale
Wolfram Engine oder gegen eine
Wolfram Engine in der Cloud ausgeführt werden . Sie können direkt Code zur Ausführung angeben:
Und damit können Sie beispielsweise Funktionen definieren, beispielsweise mit Code in einer Datei:
Zusammen mit der Veröffentlichung von Version 12.0 veröffentlichen wir auch unsere erste neue
Wolfram Language Client Library - für Python. Die Grundidee dieser Bibliothek besteht darin, Python-Programmen das Aufrufen der Wolfram-Sprache zu erleichtern. (Es ist erwähnenswert, dass wir seit nicht weniger als 30 Jahren effektiv eine C-Sprach-Client-Bibliothek haben - durch das, was jetzt
WSTP heißt.)
Die Funktionsweise einer Sprachclientbibliothek ist für verschiedene Sprachen unterschiedlich. For Python—as an interpreted language (that was actually historically informed by early Wolfram Language)—it's particularly simple. After you
set up the library , and start a session (locally or in the cloud), you can then just evaluate Wolfram Language code and get the results back in Python:
You can also directly access Wolfram Language functions (as a kind of inverse of
ExternalFunction ):
And you can directly interact with things like pandas structures, NumPy arrays, etc. In fact, you can in effect just treat the whole of the Wolfram Language like a giant library that can be accessed from Python. Or, of course, you can just use the nice, integrated Wolfram Language directly, perhaps creating external APIs if you need them.
More for the Wolfram “Super Shell”
One feature of using the Wolfram Language is that it lets you get away from having to think about the details of your computer system, and about things like files and processes. But sometimes one wants to work at a systems level. And for fairly simple operations, one can just use an operating system GUI. But what about for more complicated things? In the past I usually found myself using the
Unix shell . But for a long time now, I've instead used Wolfram Language.
It's certainly very convenient to have everything in a notebook, and it's been great to be able to programmatically use functions like
FileNames (ls),
FindList (grep),
SystemProcessData (ps),
RemoteRunProcess (ssh) and
FileSystemScan . But in Version 12.0 we're adding a bunch of additional functions to support using the Wolfram Language as a “super shell”.
There's
RemoteFile for symbolically representing a remote file (with authentication if needed)— that you can immediately use in functions like
CopyFile . There's
FileConvert for directly converting files between different formats.
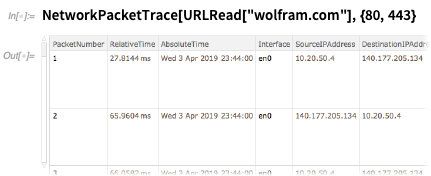
And if you really want to dive deep, here's how you'd trace all the packets on ports 80 and 443 used in reading from
wolfram.com :
Puppeting a Web Browser
Within the Wolfram Language, it's been easy for a long time to interact with web servers, using functions like
URLExecute and
HTTPRequest , as well as $
Cookies , etc. But in Version 12.0 we're adding something new: the ability of the Wolfram Language to
control a web browser , and programmatically make it do what we want. The most immediate thing we can do is just to get an image of what a website looks like to a web browser:
The result is an image that we can compute with:
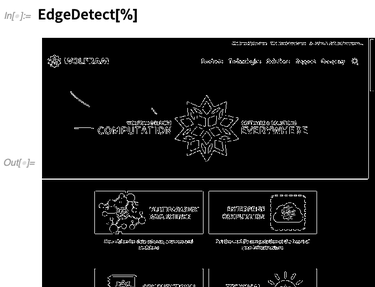
To do something more detailed, we have to start a browser session (we currently support Firefox and Chrome):
Immediately a blank browser window appears on our screen. Now we can use WebExecute to open a webpage:
Now that we've opened the page, there are lots of commands we can run. This clicks the first hyperlink containing the text “Programming Lab”:
This returns the title of the page we've reached:
You can type into fields, run JavaScript, and basically do programmatically anything you could do by hand with a web browser. Needless to say, we've been using a version of this technology for years inside our company to test all our various websites and web services. But now, in Version 12.0, we're making a streamlined version generally available.
For every general-purpose computer in the world today, there are probably 10 times as many
microcontrollers —running specific computations without any general operating system. A microcontroller might cost a few cents to a few dollars, and in something like a mid-range car, there might be 30 of them.
In Version 12.0 we're introducing a
Microcontroller Kit for the Wolfram Language, that lets you give symbolic specifications from which it automatically generates and deploys code to run autonomously in microcontrollers. In the typical setup, a microcontroller is continuously doing computations on data coming in from sensors, and in real time putting out signals to actuators. The most common types of computations are effectively ones in control theory and signal processing.
We've had extensive support for doing
control theory and
signal processing directly in the Wolfram Language for a long time. But now what's possible with the Microcontroller Kit is to take what's specified in the language and download it as embedded code in a standalone microcontroller that can be
deployed anywhere (in devices, IoT, appliances, etc.).
As an example, here's how one can generate a symbolic representation of an analog signal-processing filter:
We can use this filter directly in the Wolfram Language—say using
RecurrenceFilter to apply it to an audio signal. We can also do things like plot its frequency response:
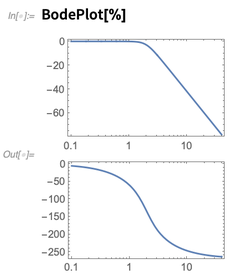
To deploy the filter in a microcontroller, we first have to derive from this continuous-time representation a discrete-time approximation that can be run in a tight loop (here, every 0.1 seconds) in the microcontroller:
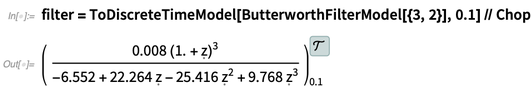
Now we're ready to use the Microcontroller Kit to actually deploy this to a microcontroller. The kit supports more than a hundred different types of microcontrollers. Here's how we could deploy the filter to an
Arduino Uno that we have connected to a serial port on our computer:
MicrocontrollerEmbedCode works by generating appropriate C-like source code, compiling it for the microcontroller architecture you want, then actually deploying it to the microcontroller through its so-called programmer. Here's the actual source code that was generated in this particular case:
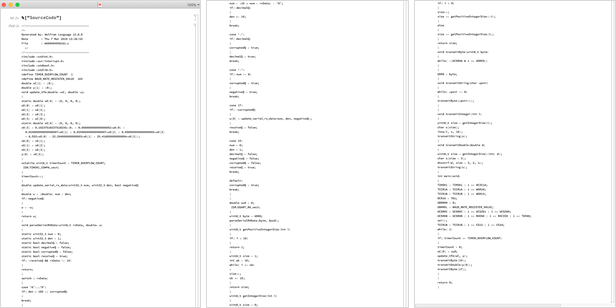
So now we have a thing like this that runs our
Butterworth filter , that we can use anywhere:
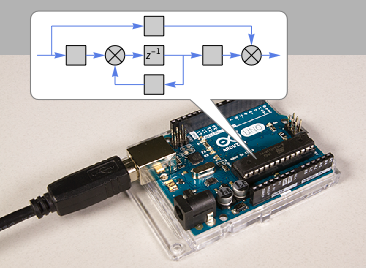
If we want to check what it's doing, we can always connect it back into the Wolfram Language using
DeviceOpen to open its
serial port , and read and write from it.
What's the relation between the Wolfram Language and video games? Over the years, the Wolfram Language has been used behind the scenes in
many aspects of game development (simulating strategies, creating geometries, analyzing outcomes, etc.). But for some time now we've been working on a closer link between Wolfram Language and the
Unity game environment , and in Version 12.0 we're releasing a first version of this link.
The basic scheme is to have Unity running alongside the Wolfram Language, then to set up two-way communication, allowing both objects and commands to be exchanged. The under-the-hood plumbing is quite complex, but the result is a nice merger of the strengths of Wolfram Language and Unity.
This sets up the link, then starts a new project in Unity:
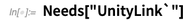
Now create some complex shape:
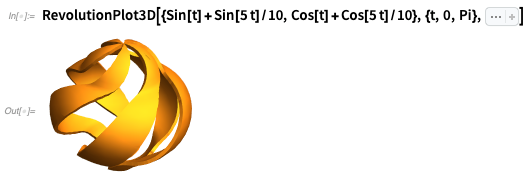
Then it takes just one command to put this into the Unity game as an object called "
thingoid ":
Within the Wolfram Language there's a symbolic representation of the object, and UnityLink now provides hundreds of functions for manipulating such objects, always maintaining versions both in Unity and in the Wolfram Language.
It's very powerful that one can take things from the Wolfram Language and immediately put them into Unity—whether they're
geometry ,
images ,
audio ,
geo terrain ,
molecular structures ,
3D anatomy , or whatever. It's also very powerful that such things can then be manipulated within the Unity game, either through things like game physics, or by user action. (Eventually, one can expect to have
Manipulate -like functionality, in which the controls aren't just sliders and things, but complex pieces of gameplay.)
We've done experiments with putting Wolfram Language–generated content into virtual reality since the early 1990s. But in modern times Unity has become something of a de facto standard for setting up VR/AR environments—and with UnityLink it's now straightforward to routinely put things from Wolfram Language into any modern XR environment.
One can use the Wolfram Language to prepare material for Unity games, but within a Unity game UnityLink also basically lets one just insert Wolfram Language code that can be executed during a game either on a local machine or through an API in the
Wolfram Cloud . And, among other things, this makes it straightforward to put hooks into a game so the game can send “telemetry” (say to the
Wolfram Data Drop ) for analysis in the Wolfram Language. (It's also possible to script the playing of the game—which is, for example, very useful for game testing.)
Writing games is a complex matter. But UnityLink provides an interesting new approach that should make it easier to prototype all sorts of games, and to learn the ideas of game development. One reason for this is that it effectively lets one script a game at a higher level by using symbolic constructs in the Wolfram Language. But another reason is that it lets the development process be done incrementally in a notebook, and explained and documented every step of the way. For example, here's what amounts to a
computational essay describing the development of a “
piano game ”:
UnityLink isn't a simple thing: it contains more than 600 functions. But with those functions it's possible to access pretty much all the capabilities of Unity, and to set up pretty much any imaginable game.
For something like reinforcement learning it's essential to have a manipulable external environment in the loop when one's doing machine learning. Well,
ServiceExecute lets you call APIs (what's the effect of posting that tweet, or making that trade?), and
DeviceExecute lets you actuate actual devices (turn the robot left) and get data from sensors (did the robot fall over?).
But for many purposes what one instead wants is to have a simulated external environment. And in a way, just the pure Wolfram Language already to some extent does that, for example providing access to a rich “computational universe” full of modifiable programs and equations (
cellular automata ,
differential equations , …). And, yes, the things in that computational universe can be informed by the real world—say with the realistic properties of
oceans , or
chemicals or
mountains .
But what about environments that are more like the ones we modern humans typically learn in—full of built engineering structures and so on? Conveniently enough,
SystemModel gives access to lots of realistic engineering systems. And through UnityLink we can expect to have access to rich game-based simulations of the world.
But as a first step, in Version 12.0 we're setting up connections to some simple games—in particular from the
OpenAI “gym” . The interface is much as it would be for interacting with the real world, with the game accessed like a “device” (after appropriate sometimes-“open-source-painful” installation):
We can read the state of the game:
And we can show it as an image:
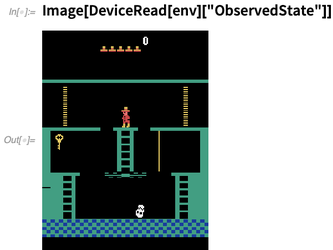
With a bit more effort, we can take 100 random actions in the game (always checking that we didn't “die”), then show a feature space plot of the observed states of the game:
In Version 11.3 we began
our first connection to the blockchain . Version 12.0 adds a lot of new features and capabilities, perhaps most notably the ability to write to public blockchains, as well as read from them. (We also have our own
Wolfram Blockchain for Wolfram Cloud users.) We're currently supporting
Bitcoin ,
Ethereum and
ARK blockchains, both their mainnets and testnets (and, yes, we have our own nodes connecting directly to these blockchains).
In Version 11.3 we allowed
raw reading of transactions from blockchains. In Version 12.0 we've added a layer of analysis, so that, for example, you can ask for a summary of “CK” tokens (AKA
CryptoKitties ) on the
Ethereum blockchain:
It's quick to look at all token transactions in history, and make a word cloud of how active different tokens have been:
But what about doing our own transaction? Let's say we want to use a
Bitcoin ATM (like the one that, bizarrely,
exists at a bagel store near me ) to transfer cash to a Bitcoin address. Well, first we create our crypto keys (and we need to make sure we remember our private key!):
Next, we have to take our public key and generate a Bitcoin address from it:
Make a QR code from that and you're ready to go to the ATM:
But what if we want to write to the blockchain ourselves? Here we'll use the Bitcoin testnet (so we're not spending real money). This shows an output from a transaction we did before—that includes 0.0002 bitcoin (ie 20,000 satoshi):
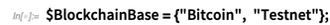
Now we can set up a transaction which takes this output, and, for example, sends 8000 satoshi to each of two addresses (that we defined just like for the ATM transaction):
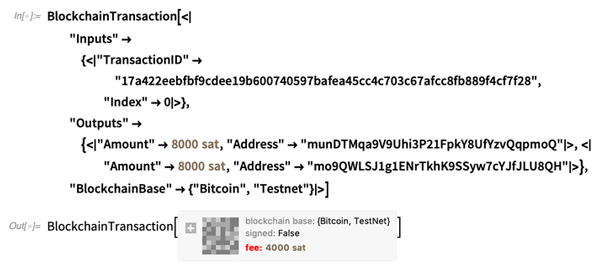
OK, so now we've got a blockchain transaction object—that would offer a fee (shown in red because it's “actual money” you'll spend) of all the leftover cryptocurrency (here 4000 satoshi) to a miner willing to put the transaction in the blockchain. But before we can submit this transaction (and “spend the money”) we have to sign it with our private key:
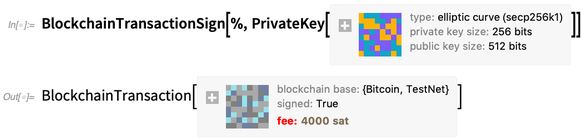
Finally, we just apply
BlockchainTransactionSubmit and we've submitted our transaction to be put on the blockchain:
Here's its transaction ID:
If we immediately ask about this transaction, we'll get a message saying it isn't in the blockchain:
But after we wait a few minutes, there it is—and it'll soon spread to every copy of the Bitcoin testnet blockchain:
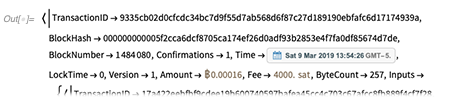
If you're prepared to spend real money, you can use exactly the same functions to do a transaction on a main net. You can also do things like buy CryptoKitties. Functions like
BlockchainContractValue can be used for any (for now, only Ethereum) smart contract, and are set up to immediately understand things like
ERC-20 and
ERC-721 tokens.
Dealing with blockchains involves lots of cryptography, some of which is new in Version 12.0 (notably, handling elliptic curves). But in Version 12.0 we're also extending our non-blockchain cryptographic functions. For example, we've now got functions for directly dealing with
digital signatures . This creates a digital signature using the private key from above:
Now anyone can verify the message using the corresponding public key:
In Version 12.0, we added several new types of hashes for the
Hash function, particularly to support various cryptocurrencies. We also added ways to generate and verify
derived keys . Start from any password, and
GenerateDerivedKey will “puff it out” to something longer (to be more secure you should add “
salt ”):
Here's a version of the derived key, suitable for use in various authentication schemes:
Connecting to Financial Data Feeds
The
Wolfram Knowledgebase contains all sorts of
financial data . Typically there's a
financial entity (like a stock), then there's a property (like price). Here's the complete daily history of Apple's stock price (it's very impressive that it looks best on a log scale):
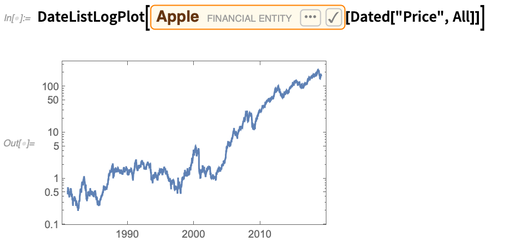
But while the financial data in the Wolfram Knowledgebase, and standardly available in the Wolfram Language, is continuously updated, it's not real time (mostly it's 15-minute delayed), and it doesn't have all the detail that many financial traders use. For serious finance use, however, we've developed
Wolfram Finance Platform . And now, in Version 12.0, it's got direct access to Bloomberg and Reuters financial data feeds.
The way we architect the Wolfram Language, the framework for the connections to Bloomberg and Reuters is always available in the language—but it's only activated if you have Wolfram Finance Platform, as well as the appropriate Bloomberg or Reuters subscriptions. But assuming you have these, here's what it looks like to connect to the
Bloomberg Terminal service:
All the financial instruments handled by the Bloomberg Terminal now become available as entities in the Wolfram Language:
Now we can ask for properties of this entity:
Altogether there are more than 60,000 properties accessible from the Bloomberg Terminal:
Here are 5 random examples (yes, they're pretty detailed; those are Bloomberg names, not ours):
We support the Bloomberg Terminal service, the
Bloomberg Data License service, and the
Reuters Elektron service. One sophisticated thing one can now do is to set up a continuous task to asynchronously receive data, and call a “
handler function ” every time a new piece of data comes in:
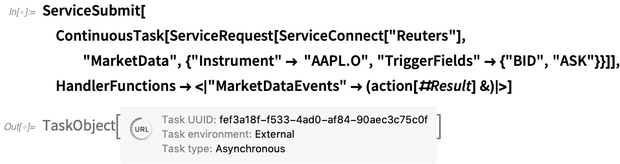
Software Engineering & Platform Updates
I've talked about lots of new functions and new functionality in the Wolfram Language. But what about the underlying infrastructure of the Wolfram Language? Well, we've been working hard on that too. For example, between Version 11.3 and Version 12.0 we've managed to fix nearly 8000 reported bugs. We've also made lots of things faster and more robust. And in general we've been tightening the software engineering of the system, for example reducing the initial download size by nearly 10% (despite all the functionality that's been added). (We've also done things like improve the predictive
prefetching of knowledgebase elements from the cloud—so when you need similar data it's more likely to be already cached on your computer.)
It's a longstanding feature of the computing landscape that operating systems are continually getting updated—and to take advantage of their latest features, applications have to get updated too. We've been working for several years on a major update to our Mac notebook interface—which is finally ready in Version 12.0. As part of the update, we've rewritten and restructured large amounts of code that have been developed and polished over more than 20 years, but the result is that in Version 12.0, everything about our system on the Mac is fully 64-bit, and makes use of the latest
Cocoa APIs . This means that the notebook front end is significantly faster—and can also go beyond the previous 2 GB memory limit.
There's also a platform update on Linux, where now the notebook interface fully supports
Qt 5 , which allows all rendering operations to take place “headlessly”, without any X server—greatly streamlining deployment of the
Wolfram Engine in the cloud. (Version 12.0 doesn't yet have high-dpi support for Windows, but that's coming very soon.)
The development of the
Wolfram Cloud is in some ways separate from the development of the Wolfram Language, and
Wolfram Desktop applications (though for internal compatibility we're releasing Version 12.0 at the same time in both environments). But in the past year since Version 11.3 was released, there's been dramatic progress in the Wolfram Cloud.
Especially notable are the advances in cloud notebooks—supporting more interface elements (including some, like embedded websites and videos, that aren't even yet available in desktop notebooks), as well as greatly increased robustness and speed. (Making our whole notebook interface work in a web browser is no small feat of software engineering, and in Version 12.0 there are some pretty sophisticated strategies for things like maintaining consistent fast-to-load caches, along with full symbolic DOM representations.)
In Version 12.0 there's now just a simple menu item (File > Publish to Cloud …) to publish any notebook to the cloud. And once the notebook is published, anyone in the world can interact with it—as well as make their own copy so they can edit it.
It's interesting to see
how broadly the cloud has entered what can be done in the Wolfram Language. In addition to all the seamless integration of the cloud knowledgebase, and the ability to reach out to things like blockchains, there are also conveniences like
Send To … sending any notebook through email, using the cloud if there's no direct email server connection available.
And a Lot Else…
Even though this has been a long piece, it's not even close to telling the whole story of what's new in Version 12.0. Along with the rest of our team, I've been working very hard on Version 12.0 for a long time now—but it's still exciting to see just how much is actually in it.
But what's critical (and a lot of work to achieve!) is that everything we've added is carefully designed to fit coherently with what's already there. From the very first version more than 30 years ago of what's now the Wolfram Language, we've been following the same core principles—and this is part of what's allowed us to so dramatically grow the system while maintaining long-term compatibility.
It's always difficult to decide exactly what to prioritize developing for each new version, but I'm very pleased with the choices we made for Version 12.0. I've given many talks over the past year, and I've been very struck with how often I've been able to say about things that come up: “Well, it so happens that that's going to be part of Version 12.0!”
I've personally been using internal preliminary builds of Version 12.0 for nearly a year, and I've come to take for granted many of its new capabilities—and to use and enjoy them a lot. So it's a great pleasure that today we have the final Version 12.0—with all these new capabilities officially in it, ready to be used by anyone and everyone…