Faltungsschicht: Techniken zur Optimierung der Matrixmultiplikation

Einführung

Dieser Artikel ist eine Fortsetzung einer Reihe von Artikeln , die die zugrunde liegenden Algorithmen beschreiben.
Synet ist ein Framework zum Starten von vorab trainierten neuronalen Netzwerken auf der CPU.

Wenn Sie sich die Verteilung der Prozessorzeit ansehen, die für die direkte Signalausbreitung in neuronalen Netzen aufgewendet wird, stellt sich heraus, dass häufig mehr als 90% aller Zeit in Faltungsschichten verbracht wird. Wenn wir also einen schnellen Algorithmus für ein neuronales Netzwerk erhalten wollen, brauchen wir zunächst einen schnellen Algorithmus für eine Faltungsschicht. In diesem Artikel möchte ich Methoden zur Optimierung der direkten Signalausbreitung in einer Faltungsschicht beschreiben. Und ich möchte mit den am weitesten verbreiteten Methoden beginnen, die auf der Matrixmultiplikation basieren. Ich werde versuchen, die Präsentation in der zugänglichsten Form zu halten, damit der Artikel nicht nur für Fachleute (sie wissen bereits alles darüber) interessant ist, sondern auch für einen größeren Leserkreis. Ich gebe nicht vor, eine vollständige Bewertung zu sein, daher sind Kommentare und Ergänzungen nur willkommen.

Faltungsschichtoptionen

Ich möchte die Beschreibung mit einer Beschreibung der Parameter beginnen, die sich in der Faltungsschicht befinden. Experten können diesen Abschnitt sicher überspringen.

Eingabe- und Ausgabebildgrößen

Zunächst wird eine Faltungsschicht durch ein Eingabe- und ein Ausgabebild charakterisiert, die durch die folgenden Parameter gekennzeichnet sind:

• srcC / dstC - Die Anzahl der Kanäle im Eingabe- und Ausgabebild. Alternative Notation: C / D.
• srcH / dstH - Höhe des Eingabe- und Ausgabebildes. Alternative Bezeichnung: H.
• srcW / dstW - Breite des Eingabe- und Ausgabebildes. Alternative Bezeichnung: W.
• Stapel - die Anzahl der Eingabe- (Ausgabe-) Bilder - Die Ebene kann einen ganzen Stapel von Bildern gleichzeitig verarbeiten. Alternative Bezeichnung: N.

Faltungskerngrößen

Die Faltungsoperation ist von Natur aus eine gewichtete Summe einer bestimmten Nachbarschaft eines bestimmten Punktes im Bild. Die Größe des Faltungskerns - charakterisiert die Größe dieser Nachbarschaft und wird durch zwei Parameter beschrieben:

• kernelY ist die Höhe des Faltungskerns. Alternative Bezeichnung: Y.
• kernelX ist die Breite des Faltungskerns. Alternative Bezeichnung: X.

Die häufigsten Windungen mit einer Kernelgröße von 1x1 und 3x3 . Größen 5x5 und 7x7 sind viel seltener. Manchmal werden auch große Faltungsgrößen sowie Faltungen mit einem anderen Kern als Quadrat gefunden, aber dies ist exotischer.

Faltungsschritt

Ein weiterer wichtiger Parameter ist der Faltungsschritt:

• Schritt Y ist der vertikale Faltungsschritt.
• strideX - horizontaler Faltungsschritt.

Wenn sich der Schritt von 1x1 unterscheidet , z. B. - 2x2 , ist das Ausgabebild halb so groß (die Faltung wird nur in der Nähe von geraden Punkten berechnet).

Dehnung der Faltung

Der Faltungskern kann mithilfe der folgenden Parameter gedehnt werden (die effektive Fenstergröße erhöhen, während die Anzahl der Operationen beibehalten wird):

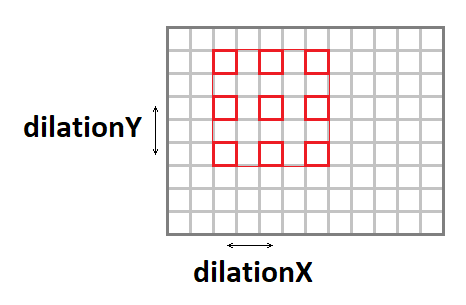
• dilationY - vertikale Dehnung der Faltung.
• dilationX - horizontale Dehnung der Faltung.

Es ist erwähnenswert, dass Fälle mit einer anderen Dehnung als 1x1 eher selten auftreten (so etwas habe ich in meiner Karriere noch nie erlebt).

Eingabebild auffüllen

Wenn Sie eine Faltung mit einem Fenster anwenden, das sich von einem einzelnen auf das Bild unterscheidet, ist das Ausgabebild um den Kernel-1- Betrag kleiner. Das Bündel „frisst“ sozusagen die Ränder. Um die Bildgröße beizubehalten, wird das Eingabebild häufig mit Nullen an den Rändern aufgefüllt. Dafür sind vier weitere Parameter verantwortlich:

• padY / padX - vertikale und horizontale Polsterung vorne.
• padH / padW - hintere vertikale und horizontale Polsterung.

Kanalgruppen

Typischerweise ist jeder Ausgangskanal die Summe der Windungen über alle Eingangskanäle. Dies ist jedoch nicht immer der Fall. Es ist möglich, die Eingangs- und Ausgangskanäle in Gruppen zu unterteilen, die Summierung erfolgt nur innerhalb der Gruppen:

• Gruppe - Die Anzahl der Gruppen.

In der Praxis treten am häufigsten Situationen mit group = 1 und group = srcC = dstC auf , der sogenannten Tiefenfaltung .

Verschiebungs- und Aktivierungsfunktion

Obwohl formale Verschiebungs- und Aktivierungsfunktionen nicht in der Faltung enthalten sind, folgen diese beiden Operationen sehr oft der Faltungsschicht, weshalb sie normalerweise auch darin enthalten sind. In Anbetracht der Vielzahl möglicher Aktivierungsfunktionen und ihrer Parameter werde ich sie hier nicht im Detail beschreiben.

Grundlegende Implementierung des Algorithmus

Zunächst möchte ich eine grundlegende Implementierung des Algorithmus geben:

float relu(float value) { return value > 0 ? return value : 0; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int b = 0; b < batch; ++b) { for (int g = 0; g < group; ++g) { for (int dc = 0; dc < dstC / group; ++dc) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { float sum = 0; for (int sc = 0; sc < srcC / group; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) sum += src[((b * srcC + sc)*srcH + sy)*srcW + sx] * weight[((dc * srcC / group + sc)*kernelY + ky)*kernelX + kx]; } } } dst[((b * dstC + dc)*dstH + dy)*dstW + dx] = relu(sum + bias[dc]); } } } } } } 

In dieser Implementierung habe ich angenommen, dass das Eingabe- und Ausgabebild im NCHW- Format vorliegt :



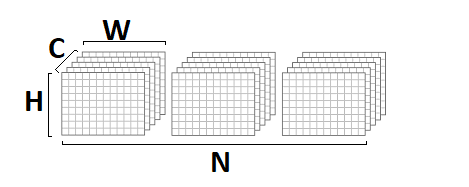
Faltungsgewichte werden im DCYX- Format gespeichert, und unsere Aktivierungsfunktion ist ReLU . Im allgemeinen Fall ist dies nicht der Fall, aber für die grundlegende Implementierung sind solche Annahmen durchaus angemessen - Sie müssen von etwas ausgehen.

Wir haben 8 verschachtelte Zyklen und die Gesamtzahl der Operationen:

 batch * kernelY * kernelX * srcC * dstH * dstW * dstC / group * 2, 

während die Datenmenge in der Eingabe:

 batch * srcC * srcH * srcW, 

und Ausgabebild:

 batch * dstC * dstH * dstW, 

und die Anzahl der Gewichte:

 kernelY * kernelX * srcC * dstC / group. 

Wenn Gruppe << srcC (die Anzahl der Gruppen ist viel kleiner als die Anzahl der Kanäle) sowie mit ausreichend großen Parametern srcC , srcH , srcW und dstC , erhalten wir ein klassisches Rechenproblem, wenn die Anzahl der Berechnungen die Menge der Eingabe- und Ausgabedaten erheblich überschreitet. Das heißt, Der Faltungsbetrieb mit ordnungsgemäßer Implementierung sollte auf den Rechenressourcen des Prozessors und nicht auf der Speicherbandbreite beruhen. Es bleibt nur diese Implementierung zu finden.

Reduktion des Problems auf Matrixmultiplikation

Die Hauptoperation bei der Faltung besteht darin, eine gewichtete Summe zu erhalten, und die Gewichte sind für alle Punkte des Ausgabebildes gleich. Wenn Sie das Eingabebild wie folgt neu anordnen:

 void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int sc = 0; sc < srcC; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[((b * srcC + sc)*srcH + sy)*srcW + sx]; else *buf++ = 0; } } } } } } 

Dann wechseln wir vom Format srcC - srcH - srcW zum Format srcC - kernelY - kernelX - dstH - dstW . Die folgende Abbildung zeigt, wie das Bild mit Padding 1 und 3x3 Core konvertiert wird:



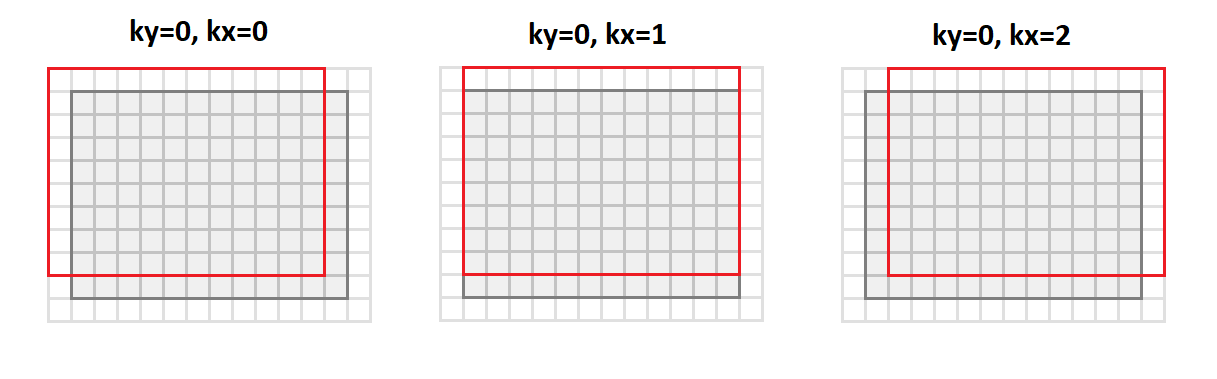
In diesem Fall werden alle Punkte der Bildumgebung, die für die Faltungsoperation erforderlich sind, entlang der Spalten der resultierenden Matrix ausgerichtet (daher der Name - Bild in Spalten).

Die neue Darstellung des Eingabebildes ist insofern interessant, als nun die Faltungsoperation in uns auf die Matrixmultiplikation reduziert wird:



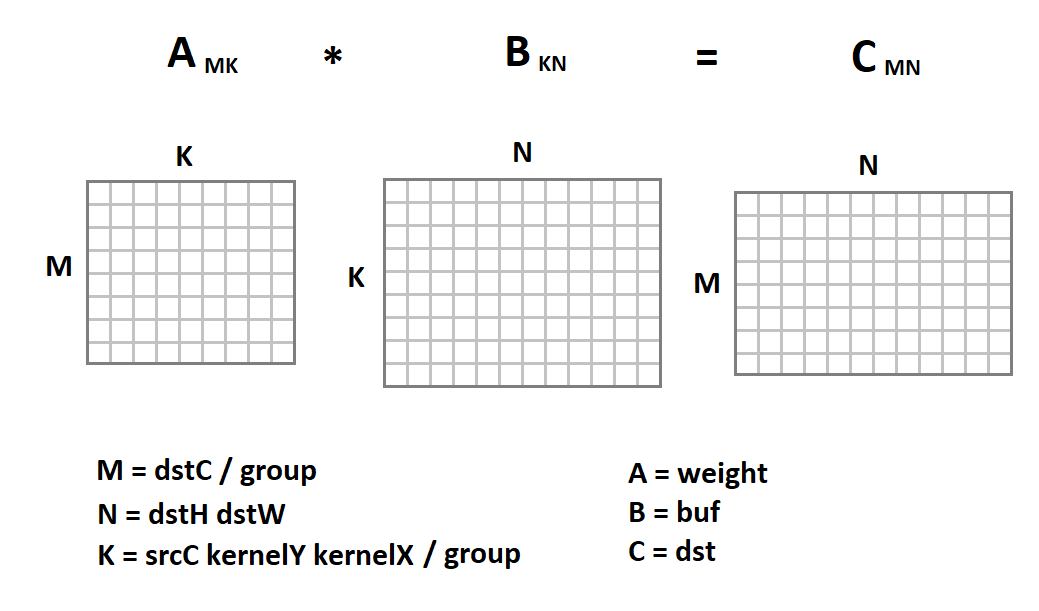
Jetzt sieht der Faltungscode folgendermaßen aus:

 void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) { for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstC / group; int N = dstH * dstW; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, weight + M * K * g, K, 0, buf + N * K * g, N, dst + M * N * g, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Hier wird die triviale Implementierung der Matrixmultiplikation nur als Beispiel gegeben. Wir können es durch jede andere Implementierung ersetzen. Glücklicherweise ist die Matrixmultiplikation eine seit langem etablierte Operation, die bereits in vielen Bibliotheken mit sehr hoher Effizienz implementiert wurde (bis zu 90% der theoretisch möglichen CPU-Leistung). Zum Thema, wie diese Effizienz erreicht wird, habe ich sogar einen separaten Artikel .

Verwenden der Matrixmultiplikation für das NHWC-Format

Neben dem NCHW- Format wird NHWC häufig beim maschinellen Lernen verwendet:



Beachten Sie beispielsweise, dass NHWC das native Tensorflow- Format ist.

Es ist bemerkenswert, dass für dieses Format die Faltungsoperation auch zu einer Matrixmultiplikation führen kann. Dazu übersetzen wir aus dem Format srcH - srcW - srcC das Originalbild mit der Funktion im2row in das Format dstH - dstW - kernelY - kernelX - srcC :

 void im2row(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int g = 0; g < group; ++g) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; for (int sc = 0; sc < srcC; ++sc) { if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[(sy * srcW + sx)*srcC + sc]; else *buf++ = 0; } } } } } src += srcC / group; } } 

Darüber hinaus sind alle Punkte der Bildumgebung, die für die Faltungsoperation erforderlich sind, entlang der Zeilen der resultierenden Matrix ausgerichtet (daher ihr Name - Bild zu Zeile s). Wir sollten auch das Speicherformat von Faltungsskalen vom DCYX- Format in das YXCD- Format ändern . Jetzt können wir die Matrixmultiplikation anwenden:



Im Gegensatz zum NCHW- Format multiplizieren wir die Bildmatrix mit der Gewichtsmatrix und nicht umgekehrt. Das Folgende ist ein Faltungsfunktionscode:

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstH * dstW; int N = dstC / group; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2row(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, group, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, buf + M * K * g, K * group, 0, weight + N * g, dstC, dst + N * g, dstC)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Vor- und Nachteile der Methode

Von Anfang an möchte ich die Vorteile dieses Ansatzes auflisten:

• Diese Methode hat eine sehr einfache Implementierung. Nicht umsonst wird es in fast allen mir bekannten Bibliotheken verwendet.
• Die Wirksamkeit der Methode ist in vielen Fällen sehr hoch: Aus Prozenteinheiten in der Basisversion erreichen wir mehr als 80% des theoretischen Maximums.
• Der Ansatz ist universell - wir haben einen Code für alle möglichen Parameter der Faltungsschicht (und es gibt viele davon!). Daher funktioniert diese Methode häufig in Fällen, in denen effektivere (und daher spezialisiertere) Ansätze Einschränkungen aufweisen.
• Der Ansatz funktioniert für die Hauptformate von Bildtensoren - NCHW und NHWC .

Nun zu den Nachteilen:

• Leider ist die Standardmatrixmultiplikation effektiv, vorausgesetzt, die Werte der Parameter M, N, K sind groß genug und außerdem ungefähr gleich groß (die Effizienz basiert auf der Tatsache, dass die erforderliche Anzahl von Berechnungen ~ O (N ^ 3) ist , und dem erforderlichen Durchsatz Gedächtnisfähigkeit ~ O (N ^ 2) ). Wenn daher einer der Parameter M, N, K klein ist, fällt die Effizienz des Verfahrens stark ab.
• Die Methode erfordert die Konvertierung von Eingabedaten. Und das ist alles andere als eine freie Operation. Sie kann nur vernachlässigt werden, wenn K groß genug ist. Und wenn wir berücksichtigen, dass es innerhalb der Standardmatrixmultiplikation immer noch eine interne Transformation der Eingabedaten gibt, wird die Situation noch trauriger.
• Basierend auf der Tatsache, dass K = srcC * kernelY * kernelX / Gruppe ist , ist die Effizienz des Verfahrens für Eingangsfaltungsschichten besonders gering. Und für die Tiefenfaltung verliert die Matrixmethode im Allgemeinen an der trivialen Implementierung.
• Das Verfahren erfordert eine zusätzliche Verarbeitung der Ausgangsdaten für den Schaltvorgang und die Berechnung der Aktivierungsfunktion.
• Es gibt effizientere mathematische Methoden zur Berechnung der Faltung, die weniger Operationen erfordern.

Schlussfolgerungen

Das Verfahren zur Berechnung der Faltung basierend auf der Matrixmultiplikation ist einfach zu implementieren und weist eine hohe Effizienz auf. Leider ist es nicht universell. Für eine Reihe von Sonderfällen gibt es schnellere Ansätze, deren Beschreibung ich auf die nächsten Artikel dieser Reihe verschieben möchte. Warten auf Feedback und Kommentare von Lesern. Ich hoffe du warst interessiert!

PS Dieser und andere Ansätze werden von mir im Convolution Framework als Teil der Simd- Bibliothek implementiert .
Dieses Framework liegt Synet zugrunde, einem Framework zum Ausführen vorab trainierter neuronaler Netze auf der CPU.