Vorwort
Vor nicht allzu langer Zeit musste ich mich mit der Vereinfachung der polygonalen Kette befassen (ein
Prozess, mit dem die Anzahl der Polylinienpunkte reduziert werden kann ). Im Allgemeinen ist diese Art von Aufgabe sehr häufig bei der Verarbeitung von Vektorgrafiken und beim Erstellen von Karten. Als Beispiel können wir eine Kette nehmen, deren mehrere Punkte in dasselbe Pixel fallen - es ist offensichtlich, dass alle diese Punkte zu einem vereinfacht werden können. Vor einiger Zeit wusste ich vom Wort „vollständig“ praktisch nichts darüber und musste daher schnell das notwendige Wissen zu diesem Thema auffüllen. Was mich jedoch überraschte, als ich im Internet nicht genügend vollständige Handbücher fand ... Ich musste Auszüge nach Informationen aus völlig anderen Quellen durchsuchen und nach der Analyse alles zu einem Gesamtbild zusammenfügen. Beruf ist nicht einer der angenehmsten, um ehrlich zu sein. Daher möchte ich eine Reihe von Artikeln über Algorithmen zur Vereinfachung der polygonalen Kette schreiben. Ich habe mich gerade entschlossen, mit dem beliebtesten Douglas-Pecker-Algorithmus zu beginnen.
Beschreibung
Der Algorithmus legt die anfängliche Polylinie und den maximalen Abstand (ε) fest, der zwischen der ursprünglichen und der vereinfachten Polylinie liegen kann (dh den maximalen Abstand von den Punkten des Originals zum nächsten Abschnitt der resultierenden Polylinie). Der Algorithmus teilt die Polylinie rekursiv. Die Eingabe in den Algorithmus sind die Koordinaten aller Punkte zwischen dem ersten und dem letzten, einschließlich dieser, sowie der Wert von ε. Der erste und der letzte Punkt bleiben unverändert. Danach findet der Algorithmus den Punkt, der am weitesten von dem Segment entfernt ist, das aus dem ersten und dem letzten besteht (
der Suchalgorithmus ist die Entfernung vom Punkt zum Segment ). Befindet sich der Punkt in einem Abstand von weniger als ε, können alle Punkte, die noch nicht zur Aufbewahrung markiert wurden, aus dem Satz ausgeworfen werden, und die resultierende gerade Linie glättet die Kurve mit einer Genauigkeit von mindestens ε. Wenn dieser Abstand größer als ε ist, ruft sich der Algorithmus rekursiv auf der Menge vom Startpunkt zum gegebenen und vom gegebenen zum Endpunkt auf.
Es ist anzumerken, dass der Douglas-Pecker-Algorithmus die Topologie im Verlauf seiner Arbeit nicht beibehält. Dies bedeutet, dass wir als Ergebnis eine Linie mit Selbstüberschneidungen erhalten können. Nehmen Sie als anschauliches Beispiel eine Polylinie mit den folgenden Punkten: [{1; 5}, {2; 3}, {5; 1}, {6; 4}, {9; 6}, {11; 4}, {13; 3}, {14; 2}, {18; 5}] und betrachten Sie den Vereinfachungsprozess für verschiedene Werte von ε:
Die ursprüngliche Polylinie aus dem dargestellten Satz von Punkten:

Polylinie mit ε gleich 0,5:
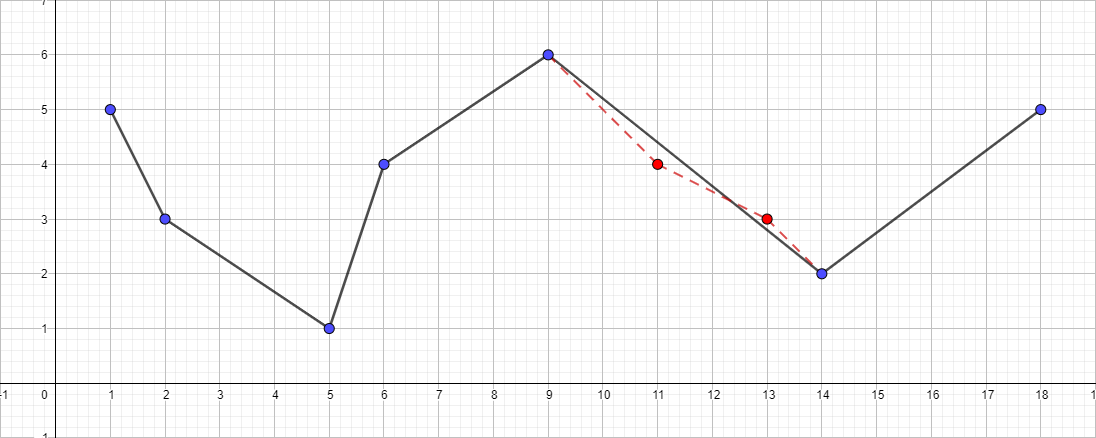
Eine Polylinie mit ε gleich 1:

Polylinie mit ε gleich 1,5:
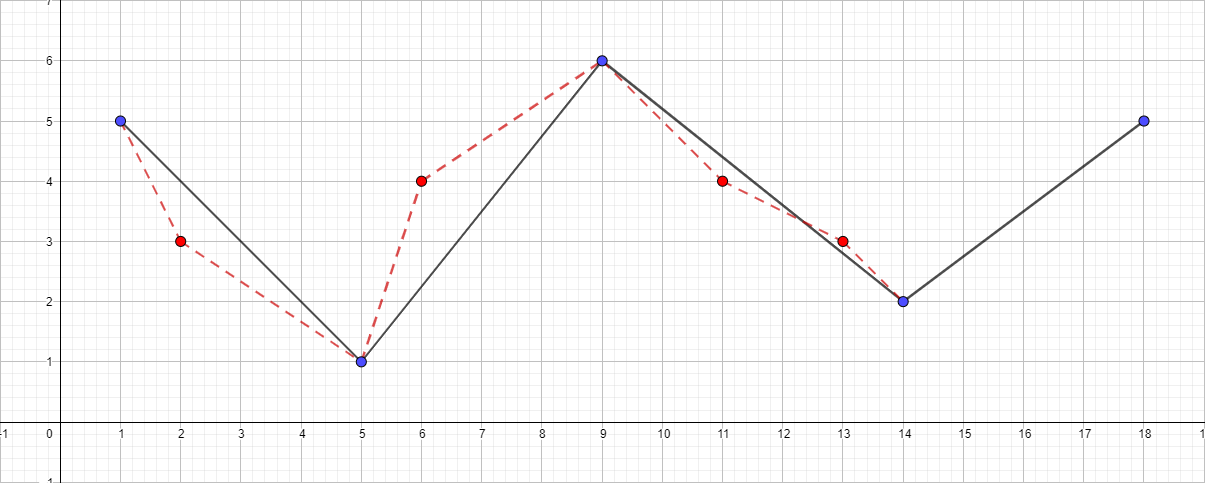
Sie können den maximalen Abstand weiter vergrößern und den Algorithmus visualisieren, aber ich denke, der Hauptpunkt nach diesen Beispielen ist klar geworden.
Implementierung
Als Programmiersprache für die Implementierung des Algorithmus wurde C ++ gewählt, der vollständige Quellcode des Algorithmus, den Sie
hier sehen können . Und jetzt direkt zur Implementierung selbst:
#define X_COORDINATE 0 #define Y_COORDINATE 1 template<typename T> using point_t = std::pair<T, T>; template<typename T> using line_segment_t = std::pair<point_t<T>, point_t<T>>; template<typename T> using points_t = std::vector<point_t<T>>; template<typename CoordinateType> double get_distance_between_point_and_line_segment(const line_segment_t<CoordinateType>& line_segment, const point_t<CoordinateType>& point) noexcept { const CoordinateType x = std::get<X_COORDINATE>(point); const CoordinateType y = std::get<Y_COORDINATE>(point); const CoordinateType x1 = std::get<X_COORDINATE>(line_segment.first); const CoordinateType y1 = std::get<Y_COORDINATE>(line_segment.first); const CoordinateType x2 = std::get<X_COORDINATE>(line_segment.second); const CoordinateType y2 = std::get<Y_COORDINATE>(line_segment.second); const double double_area = abs((y2-y1)*x - (x2-x1)*y + x2*y1 - y2*x1); const double line_segment_length = sqrt(pow((x2-x1), 2) + pow((y2-y1), 2)); if (line_segment_length != 0.0) return double_area / line_segment_length; else return 0.0; } template<typename CoordinateType> void simplify_points(const points_t<CoordinateType>& src_points, points_t<CoordinateType>& dest_points, double tolerance, std::size_t begin, std::size_t end) { if (begin + 1 == end) return; double max_distance = -1.0; std::size_t max_index = 0; for (std::size_t i = begin + 1; i < end; i++) { const point_t<CoordinateType>& cur_point = src_points.at(i); const point_t<CoordinateType>& start_point = src_points.at(begin); const point_t<CoordinateType>& end_point = src_points.at(end); const double distance = get_distance_between_point_and_line_segment({ start_point, end_point }, cur_point); if (distance > max_distance) { max_distance = distance; max_index = i; } } if (max_distance > tolerance) { simplify_points(src_points, dest_points, tolerance, begin, max_index); dest_points.push_back(src_points.at(max_index)); simplify_points(src_points, dest_points, tolerance, max_index, end); } } template< typename CoordinateType, typename = std::enable_if<std::is_integral<CoordinateType>::value || std::is_floating_point<CoordinateType>::value>::type> points_t<CoordinateType> duglas_peucker(const points_t<CoordinateType>& src_points, double tolerance) noexcept { if (tolerance <= 0) return src_points; points_t<CoordinateType> dest_points{}; dest_points.push_back(src_points.front()); simplify_points(src_points, dest_points, tolerance, 0, src_points.size() - 1); dest_points.push_back(src_points.back()); return dest_points; }
Nun, eigentlich die Verwendung des Algorithmus selbst:
int main() { points_t<int> source_points{ { 1, 5 }, { 2, 3 }, { 5, 1 }, { 6, 4 }, { 9, 6 }, { 11, 4 }, { 13, 3 }, { 14, 2 }, { 18, 5 } }; points_t<int> simplify_points = duglas_peucker(source_points, 1); return EXIT_SUCCESS; }
Beispiel für die Ausführung eines Algorithmus
Als Eingabe nehmen wir eine früher bekannte Menge von Punkten [{1; 5}, {2; 3}, {5; 1}, {6; 4}, {9; 6}, {11; 4}, {13; 3}, {14; 2}, {18; 5}] und ε gleich 1:
- Finden Sie den am weitesten vom Segment entfernten Punkt {1; 5} - {18; 5}, dieser Punkt wird der Punkt {5 sein; 1}.
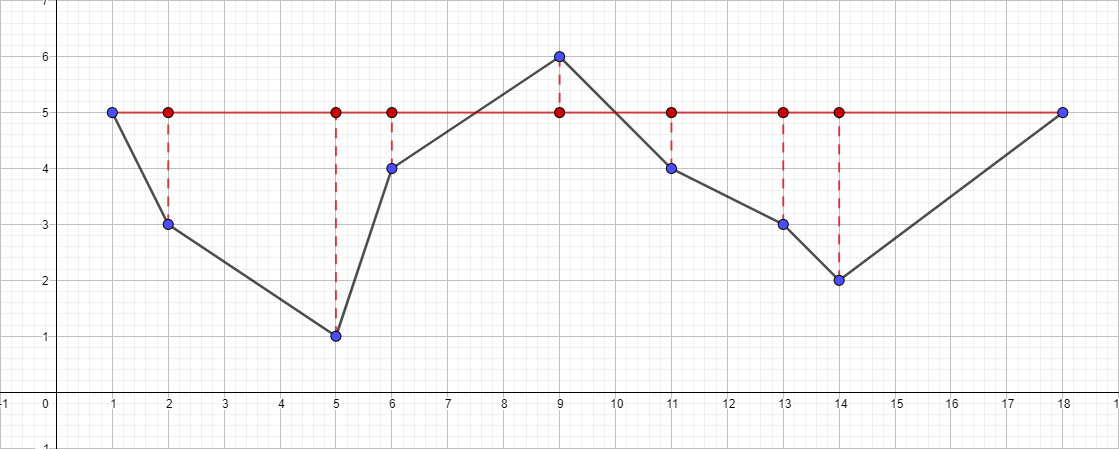
- Überprüfen Sie den Abstand zum Segment {1; 5} - {18; 5}. Es stellt sich heraus, dass es mehr als 1 ist, was bedeutet, dass wir es der resultierenden Polylinie hinzufügen.
- Führen Sie den Algorithmus für das Segment {1; 5} - {5; 1} und finden Sie den entferntesten Punkt für dieses Segment. Dieser Punkt ist {2; 3}.
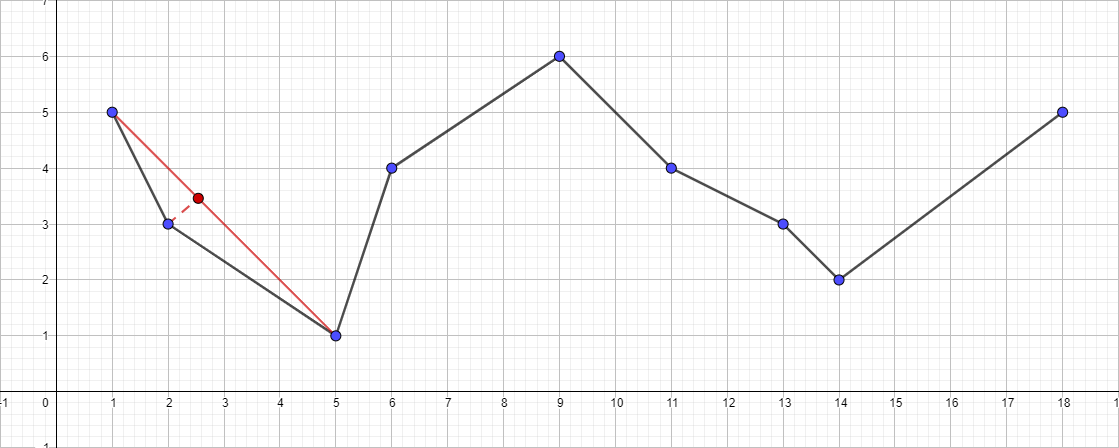
- Überprüfen Sie den Abstand zum Segment {1; 5} - {5; 1}. In diesem Fall ist es kleiner als 1, was bedeutet, dass wir diesen Punkt sicher verwerfen können.
- Führen Sie den Algorithmus für das Segment {5; 1} - {18; 5} und finde den entferntesten Punkt für dieses Segment ...
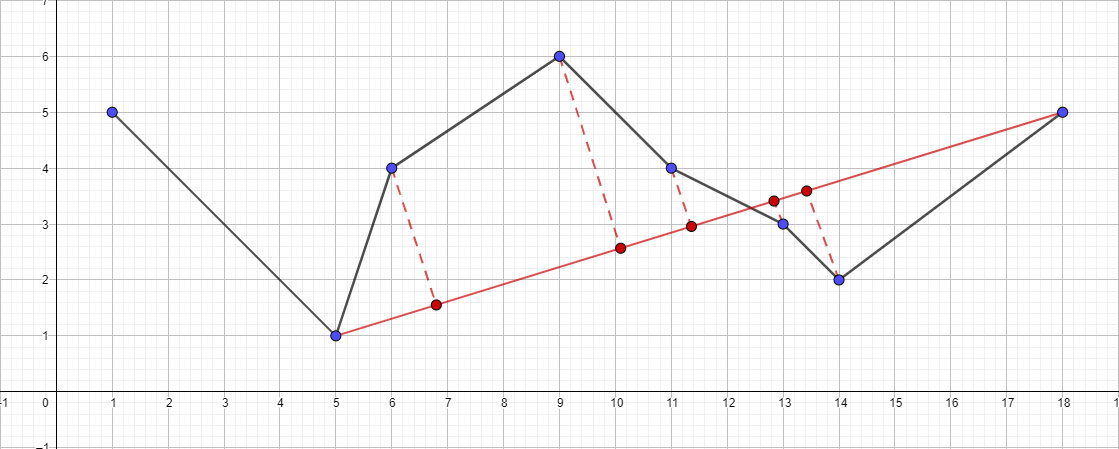
- Und so weiter nach dem gleichen Plan ...
Infolgedessen sieht der rekursive Aufrufbaum für diese Testdaten folgendermaßen aus:
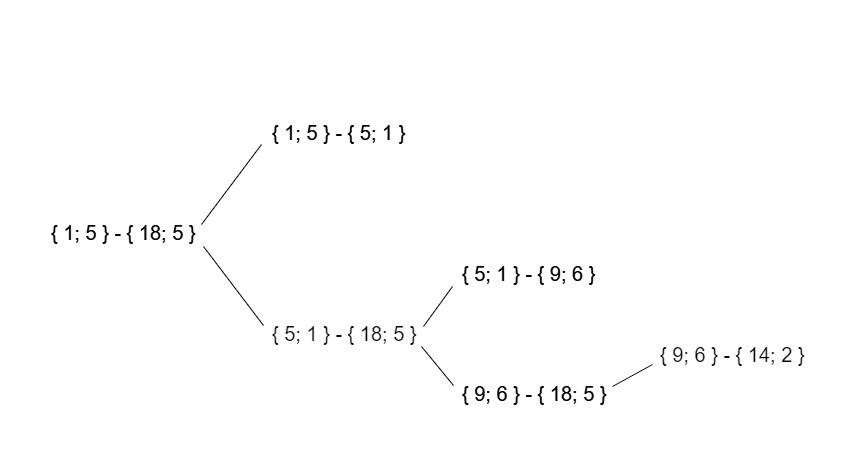
Arbeitszeit
Die erwartete Komplexität des Algorithmus ist bestenfalls O (nlogn), wenn die Nummer des am weitesten entfernten Punktes immer lexikographisch zentral ist. Im schlimmsten Fall ist die Komplexität des Algorithmus jedoch O (n ^ 2). Dies wird beispielsweise erreicht, wenn die Nummer des am weitesten entfernten Punktes immer neben der Nummer des Grenzpunktes liegt.
Ich hoffe, dass mein Artikel für jemanden nützlich sein wird. Ich möchte auch darauf hinweisen, dass ich, wenn der Artikel bei den Lesern genügend Interesse zeigt, bald bereit sein werde, Algorithmen zur Vereinfachung der polygonalen Kette von Reumman-Witkam, Opheim und Lang in Betracht zu ziehen. Vielen Dank für Ihre Aufmerksamkeit!