
Einführung
Dieser Artikel beschreibt die Ergebnisse eines Experiments, das im Rahmen des Projekts „Absoluter Wechselkurs“ durchgeführt wurde. Das Versuchsprotokoll kann durch Klicken auf den Link eingesehen werden.
Das Projekt „ Absoluter Wechselkurs “ befasst sich mit der Analyse gepaarter Wechselkurse, der Allokation absoluter Wechselkurse und deren Analyse. Im Rahmen des Projekts wurde eine Methode zur Umrechnung von Paarkursen in absolute Wechselkurse erhalten. Hierzu wird die absolute Währung ABS definiert. Alle verfügbaren Währungen werden in ABS ausgedrückt.
Eine ausführliche Beschreibung der Technologie finden Sie im Artikel „ Von Währungspaaren zu absoluten Wechselkursen “.
Bisher wurden bereits mehrere Artikel zur Anwendung der absoluten Wechselkursmethode veröffentlicht. Ich bringe die letzten beiden.
Der Artikel „ Eine Studie über die Vernetzung von Weltwährungen durch die Korrelation absoluter Wechselkurse “ beschreibt eine der Anwendungen der Technologie der absoluten Wechselkurse. Eine formale Methode zur Berechnung der Beziehung zwischen verschiedenen Währungen wird angegeben.
Der Artikel „ Die Markowitz-Portfoliomethode für den Devisenmarkt “ beschreibt bisher unzugängliche Technologien zur Optimierung des Devisenportfolios.
Im Folgenden wird die Umrechnungsmethode von paarweisen (relativen) Wechselkursen in absolute Wechselkurse beschrieben. Die numerischen Parameter der Transformation und die Methode für ihre Berechnung sind angegeben.
In der Quelldatei werden die täglichen Wechselkurse automatisch täglich geladen und die absoluten daraus berechnet.
Die Transformationsmatrix wurde 2017 erhalten. Sie wurde zu realen Paarwechselkursen berechnet, indem der Abweichungsfehler der wiederhergestellten Paarkurse vom Absoluten minimiert wurde. Seitdem wurde keine Fehleranalyse für moderne Daten durchgeführt.
Die nachstehend beschriebenen unerwarteten Verifizierungsergebnisse führten zur Entwicklung einer neuen Technik zum Erhalten der Transformationsmatrix. Außerdem wurde bei der Verarbeitung importierter Angebote ein Fehler festgestellt.
Theoretische Gründe
Um absolute Wechselkurse zu erhalten, müssen Sie die folgende Umrechnung durchführen. Zu Beginn sind gepaarte Kurse Logarithmus. Als nächstes multiplizieren wir sie mit der inversen Transformationsmatrix. Am Ende kehren wir mit einem Exponenten von der logarithmischen Skala zurück.
Für den weiteren Übergang zu Paarkursen müssen absolute Kurse protokolliert werden. Dann multiplizieren Sie mit der direkten Transformationsmatrix. Wir schließen wie zuvor mit dem Exponenten.
Die Technologie wird im Artikel „ Von Währungspaaren zu den absoluten Kursen einzelner Währungen “ ausführlicher beschrieben (nur dieser Artikel von 2018 bietet im Gegensatz zur Darstellung dieses Artikels eine transponierte Darstellung der Transformationsmatrizen).
Die direkte Matrix ist leicht zu bestimmen. Die darin enthaltenen Zeilen entsprechen Währungen, und die Spalten entsprechen den Währungspaaren. Die Matrix ist sehr dünn und besteht aus Nullen, Einsen und Minus-Einsen.
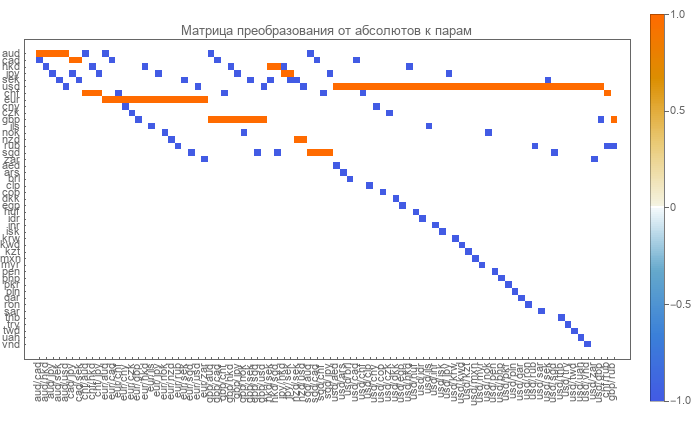
Nullen zeigen das Fehlen eines solchen Paares und einer solchen Währung an. Die Einheit entspricht der Währung im Zähler des Paares. Das Minuszeichen gibt die Währung im Nenner des Paares an.
Die inverse Transformationsmatrix von Paaren zu absoluten Raten ist nicht definiert. Es muss berechnet werden. Die naheliegendste Methode besteht darin, den Fehler bei der Paarwiederherstellung zu minimieren. Was wurde getan, um diese Matrix im Jahr 2017 zu berechnen? Wir geben eine grafische Darstellung dieser Matrix.
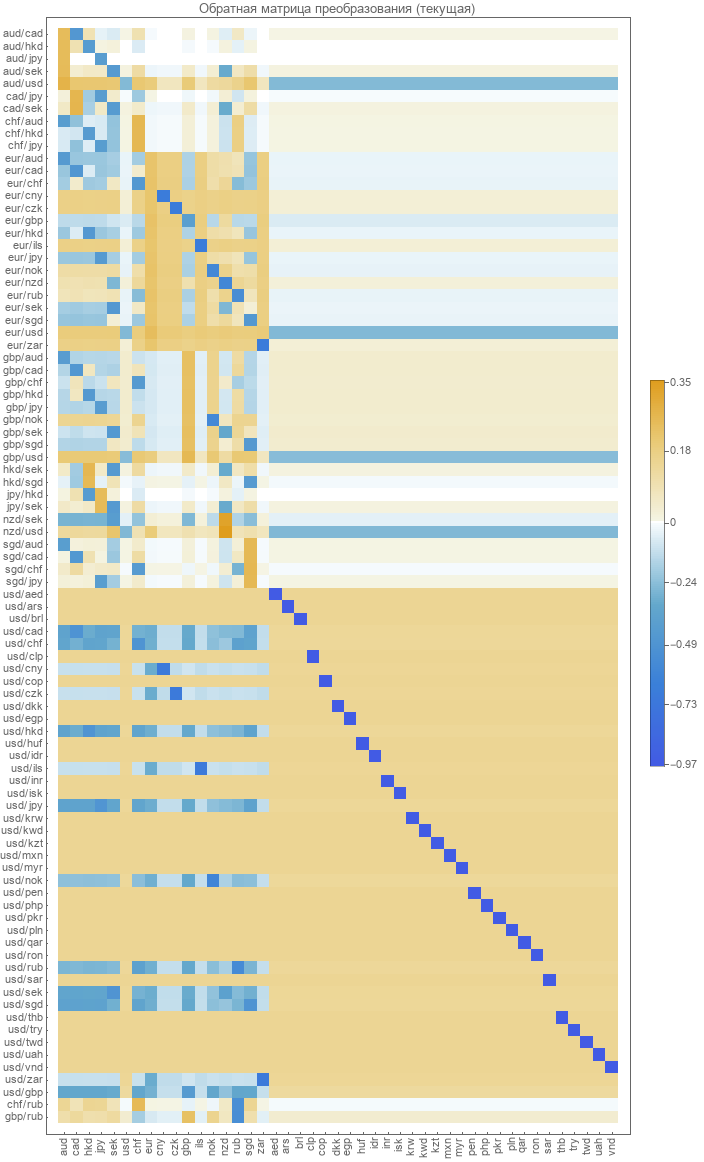
Überprüfen der Genauigkeit eines vorhandenen Modells
Für die aktuelle Matrix wurden absolute und wiederhergestellte Paarwechselkurse erhalten. Es gab starke Unterschiede zwischen den ursprünglichen und den restaurierten gepaarten Kursen.

Als nächstes wurde die Berechnung der Wiederherstellungsfehler für alle Paare durchgeführt.
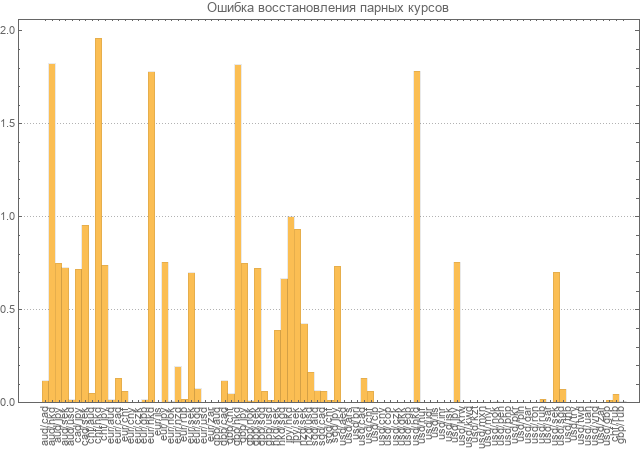
Der Fehler wurde als Durchschnitt der relativen Abweichungen betrachtet, die modulo genommen wurden. Wie im Diagramm zu sehen ist, sind die Fehler für viele Paare fast doppelt so groß wie die Werte selbst.
Diese Fehlerstufe erlaubt es natürlich nicht, das Modell als konsistent zu betrachten, und erfordert eine Nachzählung.
Pseudoinverse Matrix aus einer Linie
Als erstes werden wir versuchen, einfach die inverse Matrix für die direkte Transformationsmatrix zu berechnen. Aufgrund der Tatsache, dass die Matrix nicht quadratisch ist, müssen wir die pseudoinverse Transformation verwenden . Das Ergebnis hat Folgendes.
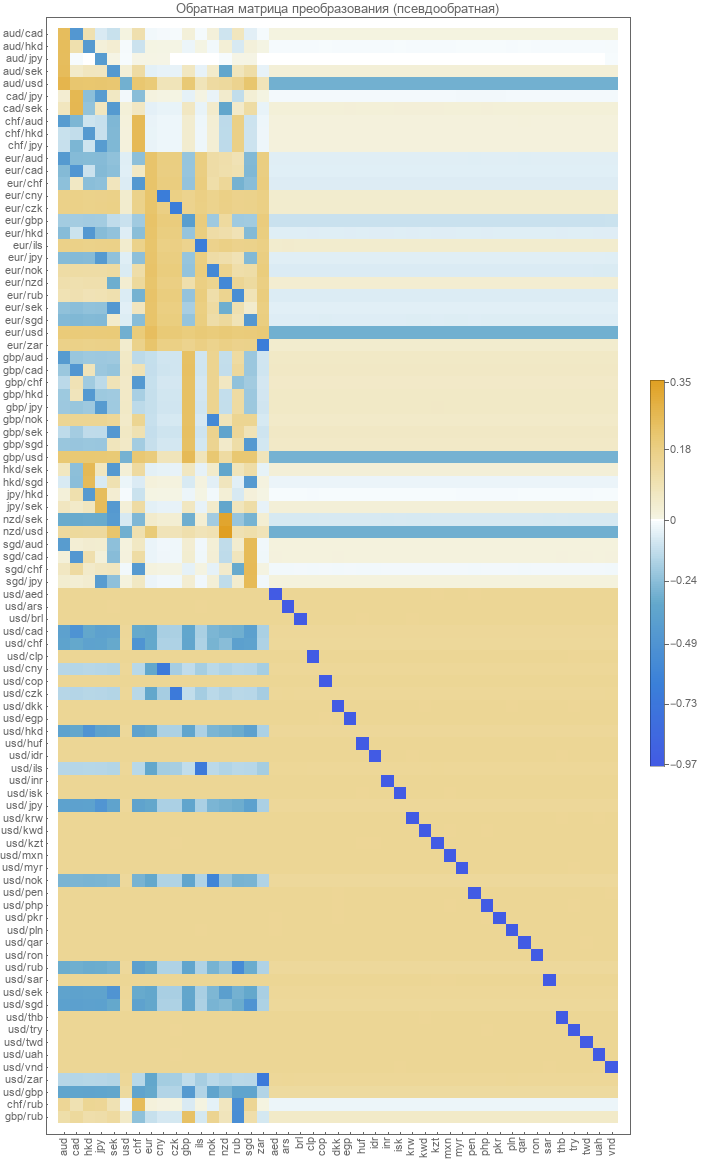
Es ist sehr ähnlich zu dem, was wir früher mit realen Paarwechselkursen zur Optimierung erhalten haben.
Wir berechnen absolute Kurse. Stellen Sie dann aus den absoluten Paarkursen wieder her. Das Fehlerdiagramm lautet wie folgt.

Die Fehler erwiesen sich ebenfalls als groß, wie in der obigen Bewertung. Dieses Modell kann auch nicht zu uns passen.
Berechnung der inversen Matrix durch linear unabhängige Komponenten
Wenn wir die direkte Transformationsmatrix im Detail analysieren, können wir feststellen, dass sie eine entartete Form hat (der Rang der Matrix ist geringer als die Anzahl der Währungszeilen). Mit anderen Worten, es gibt linear abhängige Zeilen in der direkten Matrix. Und deshalb können wir keine akzeptable inverse Matrix erhalten.
Um aus dieser Situation herauszukommen, wurde die folgende Lösung vorgeschlagen. Beim Übergang von absoluten Kursen zu gepaarten müssen Sie zunächst zu linear unabhängigen Komponenten wechseln. Und erst dann weiter zu den Paaren. Die Übergangsmatrizen von absoluten Kursen zu Komponenten und von Komponenten zu gepaarten Kursen sind nicht entartet und es können inverse Matrizen erhalten werden.
Um nach linear unabhängigen Komponenten zu suchen, muss eine Einheitsmatrix von Paarkursen an die Matrix der direkten Transformation angehängt werden. Somit erhalten wir zwei Matrizen des Übergangs von absoluten zu gepaarten Kursen und die angehängte Matrix des Übergangs von gepaarten zu gepaarten.

Jetzt werden wir Standardtransformationen in die Stufenform des oberen Teils dieser kombinierten Matrix durchführen (tatsächlich führen die Standardwerkzeuge des mathematischen Pakets Wolfram Mathematica weiter zur diagonalen Form ). Als Ergebnis war es möglich, die folgende transformierte Matrix zu erhalten.

In den Spalten dieser Matrix haben wir nun linear unabhängige Komponenten. Darüber hinaus können wir sowohl von absoluten Kursen (der obere Teil der Matrix) als auch von gepaarten Kursen (dem unteren Teil der kombinierten transformierten Matrix) zu ihnen wechseln.
Wir unterscheiden diese Übergangsmatrizen zu linear unabhängigen Komponenten. Hier ist die Übergangsmatrix für Komponenten aus absoluten Kursen.
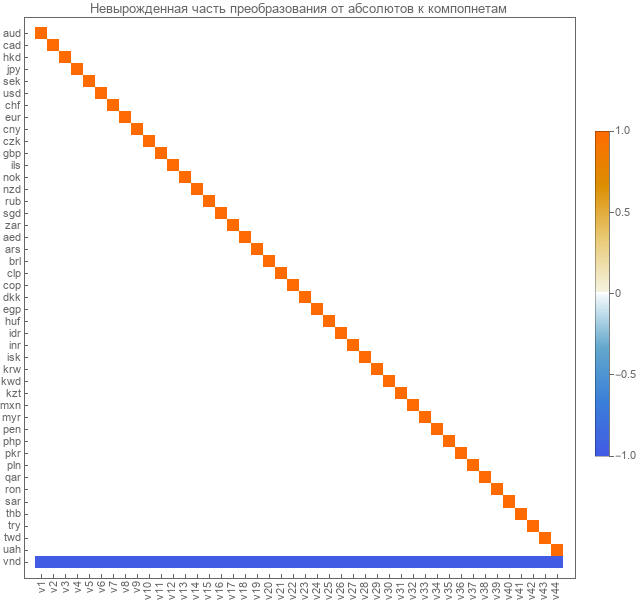
Hier ist die Übergangsmatrix von Paarkursen zu linear unabhängigen Komponenten.

Der Übergang von Absoluten zu Komponenten erfolgt über die oben berechnete Matrix. Die inverse Transformation von Komponenten zu Absoluten erfolgt über die inverse Matrix. Aufgrund der Tatsache, dass es nicht entartet ist, kann eine gute inverse Matrix erhalten werden. Wir erhalten als Pseudo-Inverse. Hier ist ihre Ansicht.

Jetzt können Sie die vollständige inverse Transformationsmatrix von Paaren zu Absoluten erhalten. Dazu multiplizieren wir die Transformationsmatrix von Paaren zu Komponenten mit der inversen Transformationsmatrix von Komponenten zu Absoluten. Sie sieht so aus.

Wir haben zwar oben schon ein ähnliches gesehen, aber die Matrix ist immer noch anders. Wir untersuchen die Ergebnisse, die es gibt. Wir werden absolute Kurse berechnen und daraus bereits gepaarte wiederherstellen. Der Wiederherstellungsfehler war wie folgt.

Bei allen Paaren außer zwei fast null Fehler. Wir finden heraus, was mit diesen Paaren nicht stimmt.
Es stellt sich heraus, dass in zwei Währungspaaren die falschen Daten akzeptiert werden. Für jpy / hkd und jpy / sek sind die Daten in vielen 10000 und 100 Teilen enthalten. Es ist notwendig, zu korrigieren und erneut zu überprüfen.
Nachdem wir die Eingabepaarkurse korrigiert (Lose entfernt) und die absoluten und wiederhergestellten Paarkurse neu berechnet haben, sehen wir uns den Wiederherstellungsfehler an.

Ich habe einen Fehler innerhalb von 0,3% erhalten. Ein ziemlich akzeptables Fehlerniveau.
Hier ist ein Beispiel für ein absolutes Kursdiagramm.
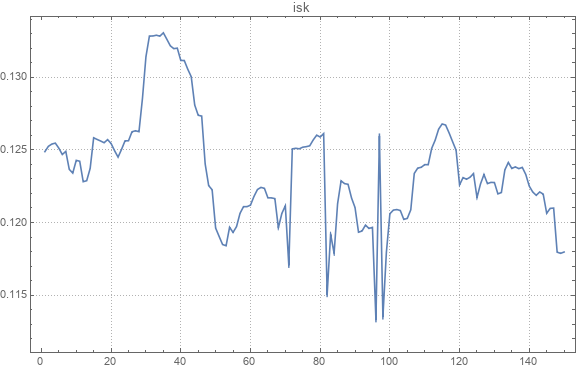
Hier ist ein Beispiel für die ursprünglichen und wiederhergestellten Paarwechselkurse.

Da wir die neue Matrix der inversen Transformation neu berechnet haben, präsentieren wir erneut Daten zu den neuesten absoluten Kursen aller teilnehmenden Währungen.
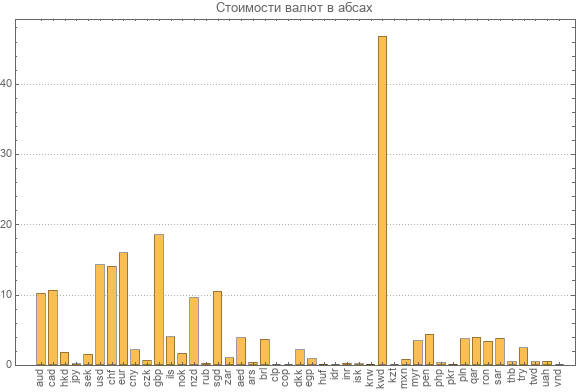
Sie können die teuerste Währung sehen. Dies ist ein kuwaitischer Dinar im Wert von fast 47 abs. Der kleinste absolute Wert des vietnamesischen Dong beträgt 0,003 abs.
Schlussfolgerungen
Als Ergebnis der Studien wurde festgestellt, dass die bestehende Methode zur Berechnung der absoluten Raten einen signifikanten Fehler ergibt. Außerdem wurde ein Fehler in den Quelldaten festgestellt.
Wir haben es geschafft, die inverse Transformationsmatrix von Paaren zu Absoluten nur unter Verwendung der Transformationsmethode in eine kleinere Anzahl linear unabhängiger Komponenten mit einer nicht entarteten Transformationsmatrix zu erhalten.
Das Verfahren zum Erhalten der inversen Transformationsmatrix verwendete keine Paarratendaten. Und damit unabhängig von ihnen.
Die Überprüfung der Konvertierung auf realen Kursen ergab eine geringe Fehlerquote. Daraus wurde geschlossen, dass die gefundene Matrix der inversen Transformation von gepaarten Wechselkursen auf absolute anwendbar ist.
Die Methode erhebt keinen Anspruch auf Vollständigkeit und mathematische Überprüfung, wird jedoch als akzeptable Lösung für weitere Untersuchungen ihrer absoluten Wechselkurse verwendet.