Dieser Artikel beschreibt die
optlib- Bibliothek, die zur Lösung globaler Optimierungsprobleme in der Sprache Rust entwickelt wurde. Zum Zeitpunkt dieses Schreibens implementiert diese Bibliothek einen genetischen Algorithmus zum Ermitteln des globalen Minimums einer Funktion. Die optlib-Bibliothek ist für eine optimierte Funktion nicht an einen bestimmten Eingabetyp gebunden. Außerdem ist die Bibliothek so aufgebaut, dass bei Verwendung des genetischen Algorithmus die Algorithmen für Kreuzung, Mutation, Selektion und andere Stufen des genetischen Algorithmus leicht geändert werden können. Tatsächlich ist der genetische Algorithmus wie aus Würfeln zusammengesetzt.
Das Problem der globalen Optimierung
Das Optimierungsproblem wird normalerweise wie folgt formuliert.
Finden Sie für eine gegebene Funktion f ( x ) unter allen möglichen Werten von x einen Wert x ', so dass f (x') einen minimalen (oder maximalen) Wert annimmt. Darüber hinaus kann x zu verschiedenen Mengen gehören - natürlichen Zahlen, reellen Zahlen, komplexen Zahlen, Vektoren oder Matrizen.
Mit dem Extremum der Funktion f ( x ) meinen wir einen Punkt x ', an dem die Ableitung der Funktion f ( x ) gleich Null ist.
Es gibt viele Algorithmen, die garantiert das Extremum der Funktion finden, das ein lokales Minimum oder Maximum in der Nähe eines bestimmten Startpunkts x 0 ist . Solche Algorithmen umfassen beispielsweise Gradientenabstiegsalgorithmen. In der Praxis ist es jedoch häufig erforderlich, das globale Minimum (oder Maximum) einer Funktion zu finden, die in einem bestimmten Bereich von x zusätzlich zu einem globalen Extremum viele lokale Extrema aufweist.
Gradientenalgorithmen können die Optimierung einer solchen Funktion nicht bewältigen, da ihre Lösung nahe dem Startpunkt zum nächsten Extremum konvergiert. Bei Problemen beim Finden eines globalen Maximums oder Minimums werden die sogenannten globalen Optimierungsalgorithmen verwendet. Diese Algorithmen garantieren nicht, ein globales Extremum zu finden, weil sind probabilistische Algorithmen, aber es bleibt nichts anderes übrig, als verschiedene Algorithmen für eine bestimmte Aufgabe auszuprobieren und herauszufinden, welcher Algorithmus die Optimierung besser bewältigen kann, vorzugsweise in kürzester Zeit und mit der maximalen Wahrscheinlichkeit, ein globales Extremum zu finden.
Einer der bekanntesten (und schwierig zu implementierenden) Algorithmen ist der genetische Algorithmus.
Das allgemeine Schema des genetischen Algorithmus
Die Idee eines genetischen Algorithmus wurde nach und nach geboren und in den späten 1960er - frühen 1970er Jahren entwickelt. Genetische Algorithmen entwickelten sich nach der Veröffentlichung von John Hollands Buch „Adaptation in Natural and Artificial Systems“ (1975) stark.
Der genetische Algorithmus basiert auf der Modellierung einer Population von Individuen über eine große Anzahl von Generationen. Im Verlauf des genetischen Algorithmus erscheinen neue Individuen mit den besten Parametern und die am wenigsten erfolgreichen Individuen sterben. Für die Bestimmtheit sind die folgenden Begriffe, die im genetischen Algorithmus verwendet werden.
- Ein Individuum ist ein Wert von x aus der Menge möglicher Werte zusammen mit dem Wert der Zielfunktion für einen gegebenen Punkt x .
- Chromosomen - der Wert von x .
- Chromosom - der Wert von x i, wenn x ein Vektor ist.
- Die Fitnessfunktion (Fitnessfunktion, Zielfunktion) ist die optimierte Funktion f ( x ).
- Eine Bevölkerung ist eine Sammlung von Individuen.
- Generation - die Anzahl der Iterationen des genetischen Algorithmus.
Jedes Individuum repräsentiert einen Wert von
x aus der Menge aller möglichen Lösungen. Der Wert der optimierten Funktion (der Kürze halber nehmen wir in Zukunft an, dass wir nach dem Minimum der Funktion suchen) wird für jeden Wert von
x berechnet. Wir gehen davon aus, dass diese Lösung umso besser ist, je weniger wichtig die Zielfunktion ist.
Genetische Algorithmen werden in vielen Bereichen eingesetzt. Sie können beispielsweise verwendet werden, um Gewichte in neuronalen Netzen auszuwählen. Viele CAD-Systeme verwenden einen genetischen Algorithmus, um Geräteparameter zu optimieren, um bestimmte Anforderungen zu erfüllen. Außerdem können globale Optimierungsalgorithmen verwendet werden, um die Position von Leitern und Elementen auf der Platine auszuwählen.
Das Strukturdiagramm des genetischen Algorithmus ist in der folgenden Abbildung dargestellt:
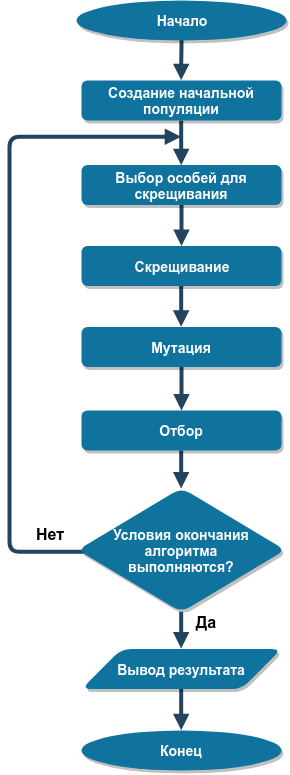
Wir betrachten jede Stufe des Algorithmus genauer.
Erstellen Sie eine Grundgesamtheit
Die erste Stufe des Algorithmus ist die Erzeugung der Anfangspopulation, dh die Erzeugung vieler Individuen mit unterschiedlichen Werten der Chromosomen x . In der Regel wird die Anfangspopulation aus Personen mit einem zufälligen Chromosomenwert erstellt, wobei versucht wird, sicherzustellen, dass die Chromosomenwerte in der Population den gesamten Lösungssuchbereich relativ gleichmäßig abdecken, es sei denn, es gibt Annahmen darüber, wo sich das globale Extremum befinden kann.
Anstatt Chromosomen zufällig zu verteilen, können Sie Chromosomen so erstellen, dass die Anfangswerte von x mit einem bestimmten Schritt gleichmäßig im Suchbereich verteilt werden. Dies hängt davon ab, wie viele Personen in dieser Phase des Algorithmus erstellt werden.
Je mehr Individuen zu diesem Zeitpunkt erstellt werden, desto größer ist die Wahrscheinlichkeit, dass der Algorithmus die richtige Lösung findet, und mit zunehmender Größe der Anfangspopulation sind in der Regel weniger Iterationen des genetischen Algorithmus (Anzahl der Generationen) erforderlich. Mit zunehmender Populationsgröße sind jedoch eine zunehmende Anzahl von Berechnungen der Zielfunktion und der Durchführung anderer genetischer Operationen in nachfolgenden Stufen des Algorithmus erforderlich. Das heißt, mit zunehmender Bevölkerungszahl erhöht sich die Berechnungszeit einer Generation.
Grundsätzlich muss die Populationsgröße nicht während der gesamten Arbeit des genetischen Algorithmus konstant bleiben, häufig kann mit zunehmender Generationszahl die Populationsgröße reduziert werden, weil Mit der Zeit wird sich eine zunehmende Anzahl von Personen näher an der gewünschten Lösung befinden. Oft wird die Bevölkerungszahl jedoch annähernd konstant gehalten.
Auswahl von Individuen für die Kreuzung
Nach der Erstellung einer Population muss festgelegt werden, welche Personen an der Kreuzung teilnehmen werden (siehe nächster Absatz). Für diese Phase gibt es verschiedene Algorithmen. Am einfachsten ist es, jedes Individuum mit jedem zu kreuzen. Im nächsten Schritt müssen Sie jedoch zu viele Kreuzungsoperationen durchführen und die Werte der Zielfunktion berechnen.
Es ist besser, eine größere Chance für die Paarung von Personen mit erfolgreicheren Chromosomen (mit einem Mindestwert der Zielfunktion) zu geben, und Personen, deren Zielfunktion mehr (schlechter) ist, die Fähigkeit zu berauben, Nachkommen zu hinterlassen.
In dieser Phase müssen Sie daher Paare von Personen erstellen (oder nicht unbedingt Paare, wenn mehr Personen an der Überfahrt teilnehmen können), für die die Überfahrt in der nächsten Stufe ausgeführt wird.
Hier können Sie auch verschiedene Algorithmen anwenden. Erstellen Sie beispielsweise Paare nach dem Zufallsprinzip. Oder Sie können Personen in aufsteigender Reihenfolge nach dem Wert der Zielfunktion sortieren und Paare von Personen erstellen, die sich näher am Anfang der sortierten Liste befinden (z. B. von Personen in der ersten Hälfte der Liste, im ersten Drittel der Liste usw.). Diese Methode ist insofern schlecht, als sie einige Zeit in Anspruch nimmt Einzelpersonen sortieren.
Die Turniermethode wird häufig verwendet. Wenn mehrere Personen zufällig für die Rolle jedes Antragstellers für die Kreuzung ausgewählt werden, wird die Person mit dem besten Wert der Zielfunktion an das zukünftige Paar gesendet. Und selbst hier kann man ein Element der Zufälligkeit einführen, das dem Individuum mit dem schlechtesten Wert der Zielfunktion eine kleine Chance gibt, das Individuum mit dem besten Wert der Zielfunktion zu "besiegen". Dies ermöglicht es Ihnen, eine heterogenere Population aufrechtzuerhalten und sie vor Degeneration zu schützen, d. H. aus einer Situation, in der alle Individuen ungefähr gleiche Chromosomenwerte haben, was dem Abwürgen des Algorithmus auf ein Extrem entspricht, möglicherweise nicht global.
Das Ergebnis dieser Operation ist eine Liste der Partner für die Überfahrt.
Kreuzung
Kreuzung ist eine genetische Operation, die neue Individuen mit neuen Chromosomenwerten erzeugt. Neue Chromosomen werden basierend auf den Chromosomen der Eltern erstellt. Meistens wird beim Überqueren einer Gruppe von Partnern eine Tochter geschaffen, aber theoretisch können mehr Kinder geschaffen werden.
Der Kreuzungsalgorithmus kann auch auf verschiedene Arten implementiert werden. Wenn der Chromosomentyp eine Zahl bei Individuen ist, ist es am einfachsten, ein neues Chromosom als arithmetisches Mittel oder geometrisches Mittel der Chromosomen der Eltern zu erstellen. Für viele Aufgaben ist dies ausreichend, aber meistens werden andere Algorithmen verwendet, die auf Bitoperationen basieren.
Bitweise Kreuze funktionieren so, dass das Tochterchromosom aus einem Teil der Bits eines Elternteils und einem Teil der Bits eines anderen Elternteils besteht, wie in der folgenden Abbildung dargestellt:
Der übergeordnete Teilungspunkt wird normalerweise zufällig ausgewählt. Es ist nicht notwendig, zwei Kinder mit einem solchen Kreuz zu schaffen, das oft auf eines von ihnen beschränkt ist.
Wenn der Teilungspunkt der Elternchromosomen eins ist, wird eine solche Kreuzung als Einzelpunkt bezeichnet. Sie können aber auch die Mehrpunktaufteilung verwenden, wenn die Elternchromosomen in mehrere Abschnitte unterteilt sind, wie in der folgenden Abbildung dargestellt:
In diesem Fall sind mehr Kombinationen von Tochterchromosomen möglich.
Wenn es sich bei den Chromosomen um Gleitkommazahlen handelt, können alle oben beschriebenen Methoden auf sie angewendet werden, sie sind jedoch nicht sehr effektiv. Wenn beispielsweise Gleitkommazahlen wie zuvor beschrieben Stück für Stück gekreuzt werden, erzeugen viele Kreuzungsoperationen Tochterchromosomen, die sich von einem der Elternteile nur in der äußersten Dezimalstelle unterscheiden. Die Situation wird besonders verschärft, wenn Gleitkommazahlen mit doppelter Genauigkeit verwendet werden.
Um dieses Problem zu lösen, muss daran erinnert werden, dass die Gleitkommazahlen gemäß dem IEEE 754-Standard als drei ganzzahlige Zahlen gespeichert sind: S (ein Bit), M und N, aus denen die Gleitkommazahl als x = (-1) S × berechnet wird M × 2 N. Eine Möglichkeit, Gleitkommazahlen zu kreuzen, besteht darin, die Zahl zuerst in Komponenten S, M, N zu unterteilen, die ganze Zahlen sind, und dann die oben beschriebenen bitweisen Kreuzungsoperationen auf die Zahlen M und N anzuwenden und das Vorzeichen S einer von auszuwählen Eltern und aus den erhaltenen Werten ein Tochterchromosom zu machen.
Bei vielen Problemen hat ein Individuum nicht nur ein, sondern mehrere Chromosomen, und es kann sogar von verschiedenen Typen sein (ganze Zahlen und Gleitkommazahlen). Dann gibt es noch mehr Möglichkeiten, solche Chromosomen zu kreuzen. Wenn Sie beispielsweise eine Tochter erstellen, können Sie alle Chromosomen der Eltern kreuzen oder einige Chromosomen ohne Änderungen vollständig von einem der Elternteile übertragen.
Mutation
Die Mutation ist eine wichtige Stufe des genetischen Algorithmus, die die Diversität einzelner Chromosomen unterstützt und somit die Wahrscheinlichkeit verringert, dass die Lösung schnell auf ein lokales Minimum anstatt auf ein globales konvergiert. Eine Mutation ist eine zufällige Veränderung des Chromosoms eines Individuums, die gerade durch Kreuzung erzeugt wurde.
In der Regel ist die Wahrscheinlichkeit einer Mutation nicht sehr hoch eingestellt, so dass die Mutation die Konvergenz des Algorithmus nicht beeinträchtigt, da sonst Personen mit erfolgreichen Chromosomen verwöhnt werden.
Neben der Kreuzung können verschiedene Algorithmen für die Mutation verwendet werden. Sie können beispielsweise ein Chromosom oder mehrere Chromosomen durch einen zufälligen Wert ersetzen. Am häufigsten wird jedoch eine bitweise Mutation verwendet, wenn ein Bit oder mehrere Bits im Chromosom (oder in mehreren Chromosomen) invertiert sind, wie in den folgenden Abbildungen gezeigt.
Mutation eines Bits:
Mutation mehrerer Bits:
Die Anzahl der Bits für eine Mutation kann entweder vordefiniert oder eine Zufallsvariable sein.
Infolge von Mutationen können sich Individuen als sowohl erfolgreicher als auch weniger erfolgreich herausstellen, aber diese Operation ermöglicht ein erfolgreiches Chromosom mit Sätzen von Nullen und Einsen, bei denen elterliche Individuen nicht mit einer Wahrscheinlichkeit ungleich Null auftreten mussten.
Auswahl
Infolge der Kreuzung und der anschließenden Mutation erscheinen neue Individuen. Wenn es keine Auswahlphase gäbe, würde die Anzahl der Individuen exponentiell zunehmen, was für jede neue Generation der Bevölkerung immer mehr RAM und Verarbeitungszeit erfordern würde. Daher ist es nach dem Auftreten neuer Individuen notwendig, die Bevölkerung von den am wenigsten erfolgreichen Individuen zu befreien. Dies geschieht in der Auswahlphase.
Auswahlalgorithmen können auch unterschiedlich sein. Oft werden Personen, deren Chromosomen nicht in ein bestimmtes Intervall einer Lösungssuche fallen, zuerst verworfen.
Sie können dann so viele der am wenigsten erfolgreichen Personen wie möglich fallen lassen, um eine konstante Bevölkerungsgröße aufrechtzuerhalten. Es können auch verschiedene Wahrscheinlichkeitskriterien für die Auswahl angewendet werden, beispielsweise kann die Wahrscheinlichkeit der Auswahl eines Individuums vom Wert der Zielfunktion abhängen.
Algorithmus-Endbedingungen
Wie in anderen Phasen des genetischen Algorithmus gibt es mehrere Kriterien zum Beenden des Algorithmus.
Das einfachste Kriterium zum Beenden eines Algorithmus besteht darin, den Algorithmus nach einer bestimmten Iterations- (Generierungs-) Nummer abzubrechen. Dieses Kriterium muss jedoch sorgfältig angewendet werden, da der genetische Algorithmus probabilistisch ist und unterschiedliche Starts des Algorithmus mit unterschiedlichen Geschwindigkeiten konvergieren können. Normalerweise wird das Beendigungskriterium durch die Iterationsnummer als zusätzliches Kriterium verwendet, falls der Algorithmus während einer großen Anzahl von Iterationen keine Lösung findet. Daher muss eine ausreichend große Zahl als Schwellenwert für die Iterationszahl festgelegt werden.
Ein weiteres Stoppkriterium ist, dass der Algorithmus unterbrochen wird, wenn für eine bestimmte Anzahl von Iterationen keine neue beste Lösung angezeigt wird. Dies bedeutet, dass der Algorithmus ein globales Extremum gefunden hat oder in einem lokalen Extremum steckt.
Es gibt auch eine ungünstige Situation, wenn die Chromosomen aller Individuen die gleiche Bedeutung haben. Dies ist die sogenannte entartete Bevölkerung. In diesem Fall steckt der Algorithmus höchstwahrscheinlich in einem Extrem und nicht unbedingt global. Nur eine erfolgreiche Mutation kann eine Population aus diesem Zustand herausholen. Da jedoch die Wahrscheinlichkeit einer Mutation normalerweise gering ist und weit davon entfernt ist, dass die Mutation ein erfolgreicheres Individuum hervorbringt, wird die Situation mit einer entarteten Population normalerweise als Entschuldigung dafür angesehen, den genetischen Algorithmus zu stoppen. Um dieses Kriterium zu überprüfen, müssen die Chromosomen aller Individuen verglichen werden, ob es Unterschiede zwischen ihnen gibt, und wenn es keine Unterschiede gibt, stoppen Sie den Algorithmus.
Bei einigen Problemen ist es nicht erforderlich, ein globales Minimum zu finden, sondern eine gute Lösung zu finden - eine Lösung, bei der der Wert der Zielfunktion unter einem bestimmten Wert liegt. In diesem Fall kann der Algorithmus vorzeitig gestoppt werden, wenn die bei der nächsten Iteration gefundene Lösung dieses Kriterium erfüllt.
optlib
Optlib ist eine Bibliothek für die Sprache Rust, die zur Optimierung von Funktionen entwickelt wurde. Zum Zeitpunkt des Schreibens dieser Zeilen ist nur der genetische Algorithmus in der Bibliothek implementiert. In Zukunft ist jedoch geplant, diese Bibliothek durch Hinzufügen neuer Optimierungsalgorithmen zu erweitern. Optlib ist vollständig in Rust geschrieben.
Optlib ist eine Open Source-Bibliothek, die unter der MIT-Lizenz vertrieben wird.
optlib :: genetisch
Aus der Beschreibung des genetischen Algorithmus ist ersichtlich, dass viele Stufen des Algorithmus auf unterschiedliche Weise implementiert werden können, indem sie ausgewählt werden, so dass der Algorithmus für eine gegebene Zielfunktion in einer minimalen Zeitspanne zur richtigen Lösung konvergiert.
Das optlib :: genetische Modul ist so konzipiert, dass der genetische Algorithmus „aus Würfeln“ zusammengesetzt werden kann. Wenn Sie eine Instanz der Struktur erstellen, in der die Arbeit des genetischen Algorithmus stattfinden wird, müssen Sie angeben, welche Algorithmen zum Erstellen der Population verwendet werden, Partner auswählen, kreuzen, mutieren, auswählen und welches Kriterium zum Unterbrechen des Algorithmus verwendet wird.
Die Bibliothek verfügt bereits über die am häufigsten verwendeten Algorithmen für die Stufen des genetischen Algorithmus. Sie können jedoch eigene Typen erstellen, die die entsprechenden Algorithmen implementieren.
In der Bibliothek ist der Fall, in dem die Chromosomen ein Vektor von Bruchzahlen sind, d.h. wenn die Funktion f ( x ) minimiert ist, wobei x der Vektor von Gleitkommazahlen ( f32 oder f64 ) ist.
Optimierungsbeispiel mit optlib :: genet
Bevor wir mit der detaillierten Beschreibung des genetischen Moduls beginnen, betrachten wir ein Beispiel für seine Verwendung zur Minimierung der Schwefel-Funktion. Diese mehrdimensionale Funktion wird wie folgt berechnet:
Die minimale Schweffel-Funktion im Intervall -500 <= x i <= 500 befindet sich am Punkt x ' , wobei alle x i = 420.9687 für i = 1, 2, ..., N und der Wert der Funktion an diesem Punkt f ( x' ) ist. = 0.
Wenn N = 2 ist, ist das dreidimensionale Bild dieser Funktion wie folgt:

Extreme werden deutlicher sichtbar, wenn wir die Ebenenlinien dieser Funktion erstellen:

Das folgende Beispiel zeigt, wie mit dem genetischen Modul die minimale Schweffel-Funktion ermittelt wird. Sie finden dieses Beispiel im Quellcode im Ordner examples / genetisch-schwefel.
Dieses Beispiel kann vom Quellstamm aus ausgeführt werden, indem der Befehl ausgeführt wird
cargo run --bin genetic-schwefel --release
Das Ergebnis sollte ungefähr so aussehen:
Solution: 420.962615966796875 420.940093994140625 420.995391845703125 420.968505859375000 420.950866699218750 421.003784179687500 421.001281738281250 421.300537109375000 421.001708984375000 421.012603759765625 420.880493164062500 420.925079345703125 420.967559814453125 420.999237060546875 421.011505126953125 Goal: 0.015625000000000 Iterations count: 3000 Time elapsed: 2617 ms
Der größte Teil des Beispielcodes ist an der Erstellung von Merkmalsobjekten für die verschiedenen Stufen des genetischen Algorithmus beteiligt. Wie am Anfang des Artikels geschrieben, kann jede Stufe des genetischen Algorithmus auf verschiedene Arten implementiert werden. Um das genetische Modul optlib :: zu verwenden, müssen Sie Merkmalsobjekte erstellen, die jeden Schritt auf die eine oder andere Weise implementieren. Anschließend werden alle diese Objekte an den Konstruktor der GeneticOptimizer-Struktur übertragen, in dem der genetische Algorithmus implementiert ist.
Die find_min () -Methode der GeneticOptimizer-Struktur startet die Ausführung des genetischen Algorithmus.
Grundtypen und Objekte
Grundzüge des optlib-Moduls
Die optlib-Bibliothek wurde mit dem Ziel entwickelt, dass in Zukunft neue Optimierungsalgorithmen hinzugefügt werden, damit das Programm problemlos von einem Optimierungsalgorithmus zu einem anderen wechseln kann. Daher enthält das optlib-Modul das Merkmal Optimizer , das eine einzige Methode enthält: find_min (), der den Optimierungsalgorithmus bei der Ausführung ausführt. Hier ist der Typ T der Typ des Objekts, der ein Punkt im Lösungssuchraum ist. Im obigen Beispiel ist dies beispielsweise Vec <Gene> (wobei Gene ein Alias für f32 ist). Das heißt, dies ist der Typ, dessen Objekt dem Eingang der Zielfunktion zugeführt wird.
Das Optimizer-Merkmal wird im optlib-Modul wie folgt deklariert:
pub trait Optimizer<T> { fn find_min(&mut self) -> Option<(&T, f64)>; }
Die find_min () -Methode des optim_-Merkmals sollte ein Objekt vom Typ Option <(& T, f64)> zurückgeben, wobei & T im zurückgegebenen Tupel die gefundene Lösung und f64 der Wert der Zielfunktion für die gefundene Lösung ist. Wenn der Algorithmus keine Lösung finden konnte, sollte die Funktion find_min () None zurückgeben.
Da viele stochastische Optimierungsalgorithmen sogenannte Agenten verwenden (im Sinne eines genetischen Algorithmus ist ein Agent ein Individuum), enthält das optlib-Modul auch das Merkmal AlgorithmWithAgents mit einer einzigen Methode get_agents (), die den Agentenvektor zurückgeben soll.
Ein Agent ist wiederum eine Struktur, die ein anderes Merkmal von optlib - Agent implementiert.
Die Merkmale AlgorithmWithAgents und Agent werden im optlib-Modul wie folgt deklariert:
pub trait AlgorithmWithAgents<T> { type Agent: Agent<T>; fn get_agents(&self) -> Vec<&Self::Agent>; } pub trait Agent<T> { fn get_parameter(&self) -> &T; fn get_goal(&self) -> f64; }
Sowohl für AlgorithmWithAgents als auch für Agent hat Typ T dieselbe Bedeutung wie für Optimizer, dh es ist der Objekttyp, für den der Wert der Zielfunktion berechnet wird.
GeneticOptimizer Structure - Implementierung eines genetischen Algorithmus
Beide Typen sind für die GeneticOptimizer- Struktur implementiert - Optimizer und AlgorithmWithAgents.
Jede Stufe des genetischen Algorithmus wird durch einen eigenen Typ dargestellt, der von Grund auf neu implementiert werden kann oder eine der darin verfügbaren optlib :: genetischen Implementierungen verwendet. Für jede Stufe des genetischen Algorithmus gibt es innerhalb des optlib :: genetischen Moduls ein Submodul mit Hilfsstrukturen und -funktionen, die die am häufigsten verwendeten Algorithmen der Stufen des genetischen Algorithmus implementieren. Über diese Module wird unten diskutiert. In einigen dieser Submodule befindet sich auch ein Submodul vec_float, das die Schritte des Algorithmus für den Fall implementiert, dass die Zielfunktion aus einem Vektor von Gleitkommazahlen (f32 oder f64) berechnet wird.
Der Konstruktor der GeneticOptimizer-Struktur wird wie folgt deklariert:
impl<T: Clone> GeneticOptimizer<T> { pub fn new( goal: Box<dyn Goal<T>>, stop_checker: Box<dyn StopChecker<T>>, creator: Box<dyn Creator<T>>, pairing: Box<dyn Pairing<T>>, cross: Box<dyn Cross<T>>, mutation: Box<dyn Mutation<T>>, selections: Vec<Box<dyn Selection<T>>>, pre_births: Vec<Box<dyn PreBirth<T>>>, loggers: Vec<Box<dyn Logger<T>>>, ) -> GeneticOptimizer<T> { ... } ... }
Der Konstruktor von GeneticOptimizer akzeptiert viele Arten von Objekten, die sich auf jede Stufe des genetischen Algorithmus sowie auf die Ausgabe der Ergebnisse auswirken:
- Ziel: Box <dyn Ziel <T>> - Zielfunktion;
- stop_checker: Box <dyn StopChecker <T>> - Stoppkriterium;
- Ersteller: Box <dyn Ersteller <T>> - erstellt die ursprüngliche Grundgesamtheit;
- Pairing: Box <dyn Pairing <T>> - Algorithmus zur Auswahl der Partner für die Kreuzung;
- cross: Box <dyn Cross <T>> - Kreuzungsalgorithmus;
- Mutation: Box <dyn Mutation <T>> - Mutationsalgorithmus;
- Auswahl: Vec <Box <dyn Auswahl <T> >> - ein Vektor von Auswahlalgorithmen;
- pre_births: Vec <Box <dyn PreBirth <T> >> - ein Vektor von Algorithmen zur Zerstörung erfolgloser Chromosomen vor der Erstellung von Individuen;
- Logger: Vec <Box <dyn Logger <T> >> - ein Vektor von Objekten, die das Log des genetischen Algorithmus beibehalten.
Um den Algorithmus auszuführen, müssen Sie die find_min () -Methode des Optimizer-Merkmals ausführen. Darüber hinaus verfügt die GeneticOptimizer-Struktur über die next_iterations () -Methode, mit der die Berechnung nach Abschluss der find_min () -Methode fortgesetzt werden kann.
Manchmal ist es nach dem Stoppen des Algorithmus nützlich, die Parameter des Algorithmus oder die verwendeten Methoden zu ändern. Dies kann mit den folgenden Methoden der GeneticOptimizer-Struktur erfolgen: replace_pairing (), replace_cross (), replace_mutation (), replace_pre_birth (), replace_selection (), replace_stop_checker (). Mit diesen Methoden können Sie die Merkmalsobjekte ersetzen, die beim Erstellen an die GeneticOptimizer-Struktur übergeben werden.
Die Haupttypen für den genetischen Algorithmus werden in den folgenden Abschnitten erläutert.
Zielmerkmal - Zielfunktion
Das Zielmerkmal wird im genetischen Modul optlib :: wie folgt deklariert:
pub trait Goal<T> { fn get(&self, chromosomes: &T) -> f64; }
Die Methode get () sollte den Wert der Zielfunktion für das angegebene Chromosom zurückgeben.
Innerhalb des optlib :: genet :: target- Moduls gibt es eine GoalFromFunction- Struktur, die das Goal- Merkmal implementiert. Für diese Struktur gibt es einen Konstruktor, der eine Funktion übernimmt, die die Zielfunktion ist. Mit dieser Struktur können Sie aus einer regulären Funktion ein Objekt vom Typ Ziel erstellen.
Schöpfermerkmal - Erstellen einer anfänglichen Population
Das Creator-Merkmal beschreibt den „Creator“ der ursprünglichen Population. Dieses Merkmal wird wie folgt deklariert:
pub trait Creator<T: Clone> { fn create(&mut self) -> Vec<T>; }
Die Methode create () sollte den Vektor der Chromosomen zurückgeben, auf dessen Grundlage die ursprüngliche Population erstellt wird.
Für den Fall, dass eine Funktion mehrerer Gleitkommazahlen optimiert wird, verfügt das optlib :: genet :: Creator :: vec_float-Modul über eine RandomCreator <G> -Struktur, mit der eine anfängliche Verteilung von Chromosomen auf zufällige Weise erstellt werden kann.
Im Folgenden ist der Typ <G> der Typ eines Chromosoms im Chromosomenvektor (manchmal wird der Begriff "Gen" anstelle des Begriffs "Chromosom" verwendet). Grundsätzlich bedeutet der Typ <G> den Typ f32 oder f64, wenn die Chromosomen vom Typ Vec <f32> oder Vec <f64> sind.
Die Struktur von RandomCreator <G> wird wie folgt deklariert:
pub struct RandomCreator<G: Clone + NumCast + PartialOrd> { ... }
Hier ist NumCast ein Typ aus der Zahlenkiste. Mit diesem Typ können Sie mit der from () -Methode einen Typ aus anderen numerischen Typen erstellen.
Um eine RandomCreator <G> -Struktur zu erstellen, müssen Sie die new () -Funktion verwenden, die wie folgt deklariert ist:
pub fn new(population_size: usize, intervals: Vec<(G, G)>) -> RandomCreator<G> { ... }
Hier ist populationsgröße die Größe der Population (die Anzahl der zu erstellenden Chromosomensätze), und Intervalle sind der Vektor von Tupeln zweier Elemente - der minimale und maximale Wert des entsprechenden Chromosoms (Gens) im Chromosomensatz, und die Größe dieses Vektors bestimmt, wie viele Chromosomen im Chromosomensatz enthalten sind jeder einzelne.
Im obigen Beispiel wurde die Schweffel-Funktion für 15 Variablen vom Typ f32 optimiert. Jede Variable muss im Bereich [-500; 500]. Das heißt, um eine Population zu erstellen, muss der Intervallvektor 15 Tupel enthalten (-500.0f32, 500.0f32).
Typpaarung - Auswahl der Partner für die Kreuzung
Das Pairing-Merkmal wird verwendet, um Personen auszuwählen, die sich kreuzen. Dieses Merkmal wird wie folgt deklariert:
pub trait Pairing<T: Clone> { fn get_pairs(&mut self, population: &Population<T>) -> Vec<Vec<usize>>; }
Die Methode get_pairs () zeigt auf die Bevölkerungsstruktur , die alle Personen in der Bevölkerung enthält. Durch diese Struktur können Sie auch die besten und schlechtesten Personen in der Bevölkerung ermitteln.
Die Pairing-Methode get_pairs () sollte einen Vektor zurückgeben, der Vektoren enthält, in denen die Indizes von Personen gespeichert sind, die sich kreuzen. Abhängig vom Kreuzungsalgorithmus (der im nächsten Abschnitt erläutert wird) können zwei oder mehr Personen kreuzen.
Wenn beispielsweise Personen mit den Indizes 0 und 10, 5 und 2, 6 und 3 gekreuzt werden, sollte die Methode get_pairs () den Vektor vec! [Vec! [0, 10], vec! [5, 2], vec! [Zurückgeben. 6, 3]].
Das optlib :: genet :: pairing-Modul enthält zwei Strukturen, die verschiedene Partnerauswahlalgorithmen implementieren.
Für die RandomPairing- Struktur wird der Pairing-Typ so implementiert, dass Partner für die Kreuzung zufällig ausgewählt werden.
Für die Turnierstruktur wird das Pairing-Merkmal so implementiert, dass die Turniermethode verwendet wird. Die Turniermethode impliziert, dass jede Person, die am Kreuz teilnimmt, eine andere Person besiegen muss (der Wert der Zielfunktion der siegreichen Person muss geringer sein). Wenn die Turniermethode eine Runde verwendet, bedeutet dies, dass zwei Personen zufällig ausgewählt werden und eine Person mit einem niedrigeren Wert der Zielfunktion unter diesen beiden Personen in die zukünftige „Familie“ gelangt. Wenn mehrere Runden verwendet werden, sollte die gewinnende Person auf diese Weise gegen mehrere zufällige Personen gewinnen.
Der Turnierstrukturkonstruktor wird wie folgt deklariert:
pub fn new(partners_count: usize, families_count: usize, rounds_count: usize) -> Tournament { ... }
Hier:
- Partners_Count - die erforderliche Anzahl von Personen zum Überqueren;
- family_count - die Anzahl der "Familien", d.h. Gruppen von Individuen, die Nachkommen hervorbringen;
- round_count - die Anzahl der Runden im Turnier.
Als weitere Modifikation der Turniermethode können Sie den Zufallszahlengenerator verwenden, um eine kleine Chance zu geben, Personen mit dem schlechtesten Wert der Zielfunktion zu besiegen, d. H. Um die Wahrscheinlichkeit des Sieges durch den Wert der Zielfunktion zu beeinflussen und je größer der Unterschied zwischen den beiden Wettbewerbern ist, desto größer ist die Chance, das beste Individuum zu gewinnen, und bei nahezu gleichen Werten der Zielfunktion würde die Wahrscheinlichkeit des Sieges eines Individuums nahe 50% liegen.
Typ Cross - Crossing
Nachdem „Familien“ von Individuen gebildet wurden, müssen Sie zum Kreuzen ihre Chromosomen kreuzen, um Kinder mit neuen Chromosomen zu bekommen. Die Kreuzungsstufe wird durch den Kreuztyp dargestellt , der wie folgt deklariert wird:
pub trait Cross<T: Clone> { fn cross(&mut self, parents: &[&T]) -> Vec<T>; }
Die cross () -Methode kreuzt eine Gruppe von Eltern. Diese Methode akzeptiert den Elternparameter - ein Ausschnitt aus Verweisen auf die Chromosomen der Eltern (nicht auf die Individuen selbst) - und sollte einen Vektor von den neuen Chromosomen zurückgeben. Die Größe der Eltern hängt vom Algorithmus zur Auswahl der Partner für die Kreuzung unter Verwendung des im vorherigen Abschnitt beschriebenen Pairing-Merkmals ab . Oft wird ein Algorithmus verwendet, der neue Chromosomen basierend auf Chromosomen von zwei Elternteilen erstellt, dann ist die Größe der Eltern gleich zwei.
Das optlib :: genet :: cross- Modul enthält Strukturen, für die der Cross-Typ mit verschiedenen Kreuzungsalgorithmen implementiert ist.
- VecCrossAllGenes - eine Struktur, die zum Kreuzen von Chromosomen entwickelt wurde, wenn jedes Individuum einen Satz von Chromosomen hat - dies ist ein Vektor. Der VecCrossAllGenes-Konstruktor akzeptiert einen Cross-Objekttyp, der auf alle Elemente der übergeordneten Chromosomenvektoren angewendet wird. In diesem Fall muss die Größe der Elternchromosomenvektoren gleich groß sein. Das obige Beispiel verwendet die VecCrossAllGenes-Struktur, da das Chromosom in den verwendeten Personen vom Typ Vec <f32> ist.
- CrossMean ist eine Struktur, die zwei Zahlen so kreuzt, dass als Tochterchromosom eine Zahl als arithmetischer Durchschnitt der Elternchromosomen berechnet wird.
- FloatCrossGeometricMean ist eine Struktur, die zwei Zahlen so kreuzt, dass als Tochterchromosom eine Zahl als geometrisches Mittel der Elternchromosomen berechnet wird. Es sollten Gleitkommazahlen als Chromosomen vorhanden sein.
- CrossBitwise - bitweise Einzelpunktkreuzung zweier Zahlen.
- FloatCrossExp - bitweise Einzelpunktkreuzung von Gleitkommazahlen. Unabhängig davon kreuzen sich Mantisse und Elternaussteller. Das Kind erhält das Zeichen von einem der Elternteile.
Das
optlib :: genet :: cross- Modul enthält auch Funktionen zum bitweisen Überkreuzen von Zahlen verschiedener Typen - Ganzzahl und Gleitkomma.
Typmutation - Mutation
Nach der Kreuzung ist es notwendig, die erhaltenen Kinder zu mutieren, um die Vielfalt der Chromosomen aufrechtzuerhalten, und die Population rutschte nicht in einen entarteten Zustand. Für die Bevölkerung ist das Merkmal Mutation vorgesehen, das wie folgt deklariert wird:
pub trait Mutation<T: Clone> { fn mutation(&mut self, chromosomes: &T) -> T; }
Die einzige mutations () -Methode des Mutationsmerkmals bezieht sich auf ein Chromosom und sollte ein möglicherweise verändertes Chromosom zurückgeben. In der Regel wird eine geringe Wahrscheinlichkeit einer Mutation festgestellt, beispielsweise einige Prozent, so dass die auf Basis der Eltern erhaltenen Chromosomen erhalten bleiben und somit die Population verbessern.
Einige Mutationsalgorithmen sind bereits im optlib :: genet :: mutations- Modul implementiert.
Dieses Modul enthält beispielsweise die VecMutation- Struktur, die ähnlich wie die VecCrossAllGenes- Struktur funktioniert , d. H. Wenn das Chromosom ein Vektor ist, akzeptiert VecMutation den Mutation-Objekttyp und wendet ihn mit einer bestimmten Wahrscheinlichkeit für alle Elemente des Vektors an, wodurch ein neuer Vektor mit mutierten Genen (Elementen des Chromosomenvektors) erstellt wird.
Das optlib :: genet :: Mutationsmodul enthält auch eine BitwiseMutation- Struktur, für die das Mutationsmerkmal implementiert ist. Diese Struktur invertiert eine gegebene Anzahl von Zufallsbits in dem an sie übertragenen Chromosom. Es wird empfohlen, diese Struktur zusammen mit der VecMutation-Struktur zu verwenden.
PreBirth-Merkmal - Vorauswahl
Nach der Kreuzung und Mutation tritt normalerweise das Selektionsstadium auf, in dem die erfolglosesten Individuen zerstört werden. Bei der Implementierung des genetischen Algorithmus in der optlib :: genetischen Bibliothek gibt es jedoch vor dem Auswahlschritt einen weiteren Schritt, bei dem nicht erfolgreiche Chromosomen verworfen werden können. Dieser Schritt wurde hinzugefügt, da die Berechnung der Zielfunktion für Einzelpersonen häufig viel Zeit in Anspruch nimmt und keine Berechnung erforderlich ist, wenn die Chromosomen nicht in das bekannte Suchintervall fallen. Zum Beispiel im obigen Beispiel Chromosomen, die nicht auf das Segment fallen [-500; 500].
Um eine solche Vorfilterung durchzuführen, ist das PreBirth-Merkmal vorgesehen , das wie folgt deklariert wird:
pub trait PreBirth<T: Clone> { fn pre_birth(&mut self, population: &Population<T>, new_chromosomes: &mut Vec<T>); }
Die einzige preBirth () -Methode des PreBirth-Merkmals ist eine Referenz auf die oben erwähnte Populationsstruktur sowie eine veränderbare Referenz auf den Chromosomenvektor new_chromosomes. Dies ist der Vektor der Chromosomen, die nach dem Mutationsschritt erhalten wurden. Die Implementierung der Methode pre_birth () sollte diejenigen Chromosomen aus diesem Vektor entfernen, die offensichtlich nicht für den Zustand des Problems geeignet sind.
Für den Fall, dass die Funktion des Vektors von Gleitkommazahlen optimiert ist, enthält das Modul optlib :: genet :: pre_birth :: vec_float die CheckChromoInterval- Struktur, mit der Chromosomen entfernt werden sollen, wenn es sich um einen Vektor von Gleitkommazahlen handelt, sowie ein Element des Vektors fällt nicht in das angegebene Intervall.
Der Konstruktor für die CheckChromoInterval-Struktur lautet wie folgt:
pub fn new(intervals: Vec<(G, G)>) -> CheckChromoInterval<G> { ... }
Hier nimmt der Konstruktor einen Tupelvektor mit zwei Elementen - dem Minimal- und Maximalwert für jedes Element im Chromosom. Daher muss die Größe des Intervallvektors mit der Größe des Chromosomenvektors von Individuen übereinstimmen. Im obigen Beispiel wurde ein Vektor von 15 Tupeln (-500,0f32, 500,0f32) als Intervalle verwendet.
Auswahl Auswahl - Auswahl
Nach vorläufiger Auswahl der Chromosomen werden Individuen erstellt und in die Population eingeordnet ( Populationsstruktur ). Bei der Erstellung von Individuen für jeden von ihnen wird der Wert der Zielfunktion berechnet. In der Auswahlphase ist es notwendig, eine bestimmte Anzahl von Personen zu vernichten, damit die Bevölkerung nicht auf unbestimmte Zeit wächst. Hierzu wird das Merkmal Selection verwendet, das wie folgt deklariert wird:
pub trait Selection<T: Clone> { fn kill(&mut self, population: &mut Population<T>); }
Ein Objekt, das das Selection-Merkmal in der kill () -Methode implementiert, muss die kill () -Methode der Individual- Struktur (individual) für jedes Individuum in der Population aufrufen, das zerstört werden muss.
Um alle Personen in einer Population zu umgehen, können Sie einen Iterator verwenden, der die IterMut () -Methode der Populationsstruktur zurückgibt.
Da beim Erstellen der GeneticOptimizer- Struktur häufig mehrere Auswahlkriterien angewendet werden müssen, akzeptiert der Konstruktor einen Vektor von Objekten vom Typ Auswahl.
Wie bei anderen Stufen des genetischen Algorithmus bietet das optlib :: genetische :: Auswahlmodul bereits mehrere Implementierungen der Auswahlstufe.
StopChecker-Merkmal - Stoppkriterium
Nach der Auswahlphase müssen Sie prüfen, ob es Zeit ist, den genetischen Algorithmus zu stoppen. Wie bereits oben erwähnt, können Sie zu diesem Zeitpunkt auch verschiedene Stoppalgorithmen verwenden. Für die Unterbrechung des Algorithmus ist das Objekt verantwortlich, für das das StopChecker-Merkmal implementiert ist, das wie folgt deklariert wird:
pub trait StopChecker<T: Clone> { fn can_stop(&mut self, population: &Population<T>) -> bool; }
Hier sollte die Methode can_stop () true zurückgeben, wenn der Algorithmus gestoppt werden kann, andernfalls sollte diese Methode false zurückgeben.
Das optlib :: genet :: stopchecker-Modul enthält mehrere Strukturen mit grundlegenden Stoppkriterien und zwei Strukturen zum Erstellen von Kombinationen aus anderen Kriterien:
- MaxIterations - Unterbrechungskriterium nach Generationsnummer. Der genetische Algorithmus stoppt nach einer bestimmten Anzahl von Iterationen (Generationen).
- GoalNotChange - ein Unterbrechungskriterium, nach dem der Algorithmus gestoppt werden soll, wenn für eine bestimmte Anzahl von Iterationen keine neue Lösung gefunden werden kann. Oder mit anderen Worten, wenn für eine bestimmte Anzahl von Generationen erfolgreichere Individuen nicht erscheinen.
- Schwellenwert - Ein Stoppkriterium, nach dem der genetische Algorithmus unterbrochen wird, wenn der Wert der Zielfunktion der derzeit besten Lösung unter dem angegebenen Schwellenwert liegt.
- CompositeAll — , ( - StopChecker). , - , .
- CompositeAny — , ( - StopChecker). , - , .
Logger —
Logger , , , . Logger :
pub trait Logger<T: Clone> {
optlib::genetic::logging , Logger:
Der Konstruktor der GeneticOptimizer- Struktur akzeptiert als letztes Argument einen Vektor von Logger-Zeichentypen, mit dem Sie die Ausgabe des Programms flexibel konfigurieren können.Funktionen zum Testen von Optimierungsalgorithmen
Schweffel-Funktion
Um die Optimierungsalgorithmen zu testen, wurden viele Funktionen mit vielen lokalen Extrema erfunden. Das Modul optlib :: testfunctions enthält mehrere Funktionen, mit denen Algorithmen getestet werden können. Zum Zeitpunkt dieses Schreibens enthält das Modul optlib :: testfunctions nur zwei Funktionen.
Eine dieser Funktionen ist die Schweffel-Funktion, über die ganz am Anfang des Artikels geschrieben wurde. Ich erinnere mich noch einmal daran, dass diese Funktion wie folgt geschrieben ist:
x' = (420.9687, 420.9687, ...). .
optlib::testfunctions schwefel . N .
, , , , .
:
x' = (1.0, 2.0,… N). .
optlib::testfunctions paraboloid .
Fazit
optlib , . ( optlib::genetic ), , , , .
optlib::genetic. . , , , , .
, . , ( , ..)
Darüber hinaus ist geplant, neben der Schweffel-Funktion neue Analysefunktionen zum Testen von Optimierungsalgorithmen hinzuzufügen.
Ich erinnere mich noch einmal an die Links, die mit der optlib-Bibliothek verbunden sind:
Ich freue mich auf Ihre Kommentare, Ergänzungen und Kommentare.