Vielseitiges und perfektes Hashing

Wir beginnen die Woche mit nützlichem Material zum Start des Kurses "Algorithmen für Entwickler" . Gute Lektüre.



1. Übersicht

Hashing ist ein großartiges praktisches Werkzeug mit einer interessanten und subtilen Theorie. Neben der Verwendung von Daten als Vokabularstruktur findet sich Hashing auch in vielen verschiedenen Bereichen, einschließlich Kryptographie und Komplexitätstheorie. In dieser Vorlesung beschreiben wir zwei wichtige Konzepte: universelles Hashing (auch als universelle Familie von Hash-Funktionen bekannt) und ideales Hashing.

Das in dieser Vorlesung hervorgehobene Material umfasst:

• Die formale Einstellung und die allgemeine Idee des Hashing.
• Universelles Hashing.
• Perfektes Hashing.

2. Einführung

Wir werden das Hauptproblem mit dem zuvor diskutierten Wörterbuch betrachten und zwei Versionen betrachten: statisch und dynamisch:

• Statisch : Bei vielen S-Elementen möchten wir sie so speichern, dass wir schnell eine Suche durchführen können.
• Zum Beispiel ein festes Wörterbuch.
• Dynamisch : Hier haben wir eine Folge von Anforderungen zum Einfügen, Suchen und möglicherweise Entfernen. Wir wollen das alles effektiv machen.

Für das erste Problem könnten wir ein sortiertes Array und eine binäre Suche verwenden. Für den zweiten könnten wir einen ausgeglichenen Suchbaum verwenden. Hashing bietet jedoch einen alternativen Ansatz, der häufig der schnellste und bequemste Weg ist, um diese Probleme zu lösen. Angenommen, Sie schreiben ein Programm für die KI-Suche und möchten bereits gelöste Situationen (Positionen auf der Tafel oder Elemente des Statusraums) speichern, um nicht dieselben Berechnungen zu wiederholen, wenn Sie erneut darauf stoßen. Hashing bietet eine einfache Möglichkeit, diese Informationen zu speichern. Es gibt auch viele Anwendungen in der Kryptographie, in Netzwerken und in der Komplexitätstheorie.

3. Hash-Grundlagen

Die formale Einstellung für das Hashing ist wie folgt.

• Die Schlüssel gehören zu einem großen Satz von U. (Stellen Sie sich zum Beispiel vor, U ist eine Sammlung aller Zeichenfolgen mit einer maximalen Länge von 80 ASCII-Zeichen.)
• Es gibt einige S-Tasten in U, die wir wirklich brauchen (Tasten können entweder statisch oder dynamisch sein). Sei N = | S |. Stellen Sie sich vor, N ist viel kleiner als die Größe von U. Zum Beispiel ist S die Menge der Schülernamen in einer Klasse, die viel kleiner als 128 ^ 80 ist.
• Wir werden Einfügungen und Suchen mit einem Array A der Größe M und einer Hash-Funktion h: U → {0, ..., M - 1} durchführen. Bei gegebenem Element x besteht die Idee des Hashings darin, dass wir es in A [h (x)] speichern möchten. Beachten Sie, dass Sie, wenn U klein wäre (z. B. 2-stellige Zeichenfolgen), x einfach in A [x] speichern könnten, wie bei der Blocksortierung. Das Problem ist, dass U groß ist, also brauchen wir eine Hash-Funktion.
• Wir brauchen eine Methode, um Kollisionen aufzulösen. Eine Kollision ist, wenn h (x) = h (y) für zwei verschiedene Schlüssel x und y ist. In dieser Vorlesung werden wir Kollisionen behandeln, indem wir jedes Element von A als verknüpfte Liste definieren. Es gibt eine Reihe anderer Methoden, aber für die Probleme, auf die wir uns hier konzentrieren werden, ist dies die am besten geeignete. Diese Methode wird als Verkettungsmethode bezeichnet. Um ein Element einzufügen, setzen wir es einfach ganz oben in die Liste. Wenn h eine gute Hash-Funktion ist, hoffen wir, dass die Listen klein sind.

Eines der großartigen Dinge beim Hashing ist, dass alle Wörterbuchoperationen unglaublich einfach zu implementieren sind. Um nach dem Schlüssel x zu suchen, berechnen Sie einfach den Index i = h (x) und gehen Sie dann die Liste in A [i] durch, bis Sie ihn finden (oder verlassen Sie die Liste). Platzieren Sie zum Einfügen einfach ein neues Element oben in der Liste. Zum Löschen müssen Sie nur den Löschvorgang in der verknüpften Liste ausführen. Nun wenden wir uns der Frage zu: Was brauchen wir, um eine gute Leistung zu erzielen?

Wünschenswerte Eigenschaften. Wichtige wünschenswerte Eigenschaften für ein gutes Hash-Schema:

1. Die Schlüssel sind gut verteilt, sodass wir nicht zu viele Kollisionen haben, da Kollisionen die Such- und Löschzeit beeinflussen.
2. M = O (N): Insbesondere möchten wir, dass unsere Schaltung die Eigenschaft (1) erreicht, ohne dass die Größe der Tabelle M viel größer als die Anzahl der Elemente N sein muss.
3. Die Funktion h muss schnell berechnet werden. In unserer heutigen Analyse werden wir die Zeit zur Berechnung von h (x) als Konstante betrachten. Es ist jedoch zu beachten, dass dies nicht zu kompliziert sein sollte, da es sich auf die Gesamtausführungszeit auswirkt.

Vor diesem Hintergrund beträgt die Suchzeit für das Element x O (die Größe der Liste beträgt A [h (x)]). Gleiches gilt für Löschungen. Einfügungen benötigen O (1) Zeit, unabhängig von der Länge der Listen. Wir möchten also analysieren, wie groß diese Listen sind.

Grundlegende Intuition: Eine Möglichkeit, Elemente schön zu verteilen, besteht darin, sie zufällig zu verteilen. Leider können wir nicht einfach den Zufallszahlengenerator verwenden, um zu entscheiden, wohin das nächste Element geleitet werden soll, da wir es dann nie wieder finden können. Wir wollen also, dass h in einem formalen Sinne etwas „Pseudozufälliges“ ist.

Jetzt werden wir einige schlechte Nachrichten und dann einige gute Nachrichten präsentieren.

Anweisung 1 (schlechte Nachrichten) Für jede Hash-Funktion h if | U | ≥ (N −1) M +1 gibt es eine Menge S von N Elementen, die alle an einer Stelle gehasht haben.

Beweis: nach dem Dirichlet-Prinzip. Um Kontrapunkte zu berücksichtigen, könnte U eine Größe von nicht mehr als M (N - 1) haben, wenn jeder Ort nicht mehr als N - 1 Elemente von U hat, die ihn hashen.

Dies ist teilweise der Grund, warum Hashing so mysteriös erscheint - wie kann argumentiert werden, dass Hashing gut ist, wenn Sie sich für eine Hash-Funktion Möglichkeiten ausdenken können, dies zu verhindern? Eine Antwort ist, dass es viele einfache Hash-Funktionen gibt, die in der Praxis für typische S-Mengen gut funktionieren. Aber was ist, wenn wir eine gute Garantie für den schlimmsten Fall wollen?

Hier ist die Schlüsselidee: Verwenden wir die Randomisierung in unserem h-Konstrukt, ähnlich wie bei der randomisierten Quicksortierung. (Unnötig zu sagen, dass h eine deterministische Funktion sein wird). Wir werden zeigen, dass für jede Sequenz von Einfüge- und Suchoperationen (wir müssen nicht annehmen, dass die Menge der eingefügten Elemente S zufällig ist), wenn wir h auf diese probabilistische Weise wählen, die Leistung von h in dieser Sequenz in Erwartung gut ist. Dies ist also die gleiche Garantie wie bei randomisierten Quicksort oder Fallen. Dies ist insbesondere die Idee des universellen Hashing.

Sobald wir diese Idee entwickelt haben, werden wir sie für eine besonders unterhaltsame Anwendung namens „Perfect Hashing“ verwenden.

4. Universelles Hashing

Definition 1. Ein randomisierter Algorithmus H zur Konstruktion von Hash-Funktionen h: U → {1, ..., M}
universell, wenn wir für alle x! = y in U haben



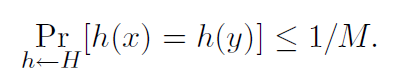
Wir können auch sagen, dass die Menge H von Hash-Funktionen eine universelle Familie von Hash-Funktionen ist, wenn die Prozedur „zufällig ausgewählte h ∈ H“ universell ist. (Hier identifizieren wir den Satz von Funktionen mit einer gleichmäßigen Verteilung über den Satz.)

Satz 2. Wenn H universell ist, dann für jede Menge S ⊆ U der Größe N, für jedes x ∈ U (zum Beispiel, nach dem wir suchen könnten), wenn wir h zufällig gemäß H konstruieren, die erwartete Anzahl von Kollisionen zwischen x und anderen Elemente in S nicht mehr als N / M.

Beweis: Jedes y ∈ S (y! = X) hat nach der Definition von „universal“ höchstens 1 / M Chance auf eine Kollision mit x. Also

• Sei Cxy = 1, wenn x und y kollidieren, andernfalls 0.
• Cx bezeichne die Gesamtzahl der Kollisionen für x. Also, Cx = Py∈S, y! = X Cxy.
• Wir wissen, dass E [Cxy] = Pr (x und y kollidieren) ≤ 1 / M ist.
• Somit ist in der Linearität der Erwartung E [Cx] = Py E [Cxy] <N / M.

Jetzt erhalten wir die folgende Folgerung.

Folgerung 3. Wenn H universell ist, betragen für jede Folge von Einfüge-, Such- und Löschoperationen L, in denen nicht mehr als M Elemente gleichzeitig in einem System vorhanden sein können, die erwarteten Gesamtkosten von L Operationen für ein zufälliges h ∈ H nur O (L) (Betrachtung der Zeit) h als Konstanten berechnen).

Beweis: Für jede gegebene Operation in der Sequenz sind ihre erwarteten Kosten gemäß Satz 2 konstant, so dass die erwarteten Gesamtkosten von L Operationen O (L) in der Linearität der Erwartung sind.

Frage: Können wir tatsächlich ein universelles H bauen? Wenn nicht, dann ist das alles ziemlich sinnlos. Zum Glück lautet die Antwort ja.

4.1. Erstellen einer universellen Hash-Familie: Matrix-Methode

Angenommen, die Schlüssel sind U-Bits lang. Angenommen, die Größe der Tabelle M ist gleich Grad 2, daher ist der Index mit M = 2b b-Bit lang.

Wir wählen h als Zufallsmatrix 0/1 b-by-u und definieren h (x) = hx, wobei wir Mod 2 hinzufügen. Diese Matrizen sind kurz und dick. Zum Beispiel:



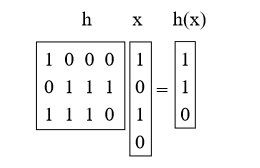
Satz 4. Für x! = Y Prh [h (x) = h (y)] = 1 / M = 1 / 2b.

Beweis: Was bedeutet es, h mit x zu multiplizieren? Wir können uns vorstellen, dass einige der Spalten h hinzugefügt werden (Vektoraddition mod 2), wobei 1 Bit in x angibt, welche hinzugefügt werden sollen. (Zum Beispiel haben wir die 1. und 3. Spalte von h oben hinzugefügt.)

Nehmen Sie nun ein beliebiges Schlüsselpaar x, y, so dass x! = Y ist. Sie müssen irgendwo unterschiedlich sein, damit sie sich beispielsweise in der i-ten Koordinate unterscheiden, und der Vollständigkeit halber sagen wir xi = 0 und yi = 1. Stellen Sie sich vor, wir hätten zuerst alle h außer der i-ten Spalte ausgewählt. Für die verbleibenden Proben der i-ten Spalte ist h (x) festgelegt. Jede der 2b unterschiedlichen Einstellungen der i-ten Spalte ergibt jedoch einen anderen Wert von h (y) (insbesondere jedes Mal, wenn wir ein Bit in dieser Spalte drehen, verwandeln wir das entsprechende Bit in h (y)). Es besteht also genau eine 1 / 2b-Chance, dass h (x) = h (y) ist.

Es gibt andere Methoden zum Aufbau universeller Hash-Familien, die ebenfalls auf der Multiplikation von Primzahlen basieren (siehe Abschnitt 6.1).

Die nächste Frage, die wir uns stellen werden: Wenn wir die Menge S korrigieren, können wir eine Hash-Funktion h finden, so dass alle Suchvorgänge eine konstante Zeit haben? Die Antwort lautet ja, und dies führt zum Thema perfektes Hashing.

5. Perfektes Hashing

Wir sagen, dass eine Hash-Funktion für S ideal ist, wenn alle Suchen in O (1) stattfinden. Hier sind zwei Möglichkeiten, um perfekte Hash-Funktionen für eine bestimmte Menge S zu erstellen.

5.1 Methode 1: eine Lösung im Raum O (N2)

Angenommen, wir möchten eine Tabelle haben, deren Größe quadratisch in der Größe N unseres Wörterbuchs S ist. Dann ist hier eine einfache Methode zum Erstellen einer idealen Hash-Funktion. Sei H universell und M = N2. Dann wählen Sie einfach ein zufälliges h aus H und probieren Sie es aus! Die Aussage ist, dass es eine mindestens 50% ige Chance gibt, dass sie keine Kollisionen hat.

Satz 5. Wenn H universell ist und M = N2, dann ist Prh∼H (keine Kollisionen in S) ≥ 1/2.

Beweis:

• Wie viele Paare (x, y) gibt es in S? Die Antwort lautet:
• Für jedes Paar beträgt die Wahrscheinlichkeit ihrer Kollision per Definition der Universalität ≤ 1 / M.
• Also Pr (es gibt eine Kollision) ≤ / M <1/2.

Dies ist wie die andere Seite des "Geburtstagsparadoxons". Wenn die Anzahl der Tage viel größer ist als die Anzahl der Personen im Quadrat, besteht eine vernünftige Chance, dass kein Paar denselben Geburtstag hat.

Wir wählen also einfach ein zufälliges h aus H aus, und wenn Kollisionen auftreten, wählen wir einfach ein neues h aus. Im Durchschnitt müssen wir dies nur zweimal tun. Was ist nun, wenn wir nur den O (N) -Raum verwenden möchten?

5.2 Methode 2: eine Lösung im Raum O (N)

Die Frage, ob es möglich ist, ein perfektes Hashing im O (N) -Raum zu erreichen, ist seit einiger Zeit offen: "Sollten die Tabellen sortiert werden?" Das heißt, für eine feste Menge können Sie eine konstante Suchzeit nur mit linearem Raum erhalten? Es gab eine Reihe immer komplexerer Versuche, bis sie schließlich mit der guten Idee universeller Hash-Funktionen in einem zweistufigen Schema gelöst wurden.

Das Verfahren ist wie folgt. Zuerst werden wir mit Universal Hashing in eine Tabelle der Größe N hashen. Dies führt zu einigen Kollisionen (es sei denn, wir haben Glück). Dann wärmen wir jedoch jeden Korb mit Methode 1 erneut auf und quadrieren die Korbgröße, um keine Kollisionen zu erhalten. Das Schema besteht also darin, dass wir eine Hash-Funktion der ersten Ebene h und eine Tabelle A der ersten Ebene haben und dann N Hash-Funktionen der zweiten Ebene h1, ..., hN und N der Tabelle der zweiten Ebene A1, ..., . ... Um das Element x zu finden, berechnen wir zuerst i = h (x) und dann das Element in Ai [hi (x)]. (Wenn Sie dies in der Praxis tun würden, könnten Sie das Flag so setzen, dass Sie den zweiten Schritt nur dann ausführen, wenn es wirklich Konflikte mit dem Index i gibt, andernfalls würden Sie einfach x selbst in A [i] setzen, aber lassen Sie uns Machen wir uns hier keine Sorgen.)

Angenommen, eine Hash-Funktion h hasht n Elemente von S an Position i. Wir haben bereits bewiesen (durch Analyse von Methode 1), dass wir h1, ..., hN finden können, so dass der in den sekundären Tabellen verwendete Gesamtraum Pi (ni) 2 ist. Es bleibt zu zeigen, dass wir eine Funktion h der ersten Ebene finden können, so dass Pi (ni) 2 = O (N). In der Tat werden wir Folgendes zeigen:

Satz 6. Wenn wir den Startpunkt h aus der universellen Menge H wählen, dann

Pr[X i (ni)2 > 4N] < 1/2. 

Beweis. Beweisen wir dies, indem wir zeigen, dass E [Pi (ni) 2] <2N ist. Dies impliziert, was wir von der Markov-Ungleichung wollen. (Wenn es eine Wahrscheinlichkeit von sogar 1/2 gäbe, dass die Summe mehr als 4 N betragen könnte, würde diese Tatsache allein bedeuten, dass die Erwartung mehr als 2 N betragen sollte. Wenn also die Erwartung weniger als 2 N beträgt, sollte die Ausfallwahrscheinlichkeit geringer sein 1/2.)

Der knifflige Trick besteht nun darin, dass eine Möglichkeit zur Berechnung dieses Betrags darin besteht, die Anzahl der geordneten Paare zu zählen, die eine Kollision haben, einschließlich Kollisionen mit sich selbst. Wenn der Korb beispielsweise {d, e, f} hat, hat d einen Konflikt mit jedem von {d, e, f}, e hat einen Konflikt mit jedem von {d, e, f} und f hat einen Konflikt mit jedes von {d, e, f}, also bekommen wir 9. Also haben wir:

 E[X i (ni)2] = E[X x X y Cxy] (Cxy = 1 if x and y collide, else Cxy = 0) = N +X x X y6=x E[Cxy] ≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal) < 2N. (since M = N) 

Also versuchen wir einfach ein zufälliges h von H, bis wir eines finden, so dass Pi n2 i <4N ist, und dann, indem wir diese Funktion h fixieren, finden wir N sekundäre Hash-Funktionen h1, ..., hN wie in Methode 1.

6. Weitere Diskussion

6.1 Eine weitere universelle Hashing-Methode

Hier ist eine andere Methode zum Erstellen universeller Hash-Funktionen, die etwas effizienter ist als die zuvor angegebene Matrixmethode.

Bei der Matrixmethode haben wir den Schlüssel als einen Bitvektor betrachtet. Bei dieser Methode betrachten wir stattdessen den Schlüssel x als einen Vektor von ganzen Zahlen [x1, x2, ..., xk] mit der einzigen Anforderung, dass jedes xi im Bereich {0, 1, ..., M-1} liegt. Wenn wir beispielsweise Zeichenfolgen der Länge k hashen, kann xi das i-te Zeichen (wenn die Größe unserer Tabelle mindestens 256 beträgt) oder das i-te Zeichenpaar (wenn die Größe unserer Tabelle mindestens 65536 beträgt) sein. Außerdem müssen die Größe unserer Tabelle M eine Primzahl sein. Um die Hash-Funktion h auszuwählen, wählen wir k Zufallszahlen r1, r2, ..., pk aus {0, 1, ..., M - 1} und bestimmen:

 h(x) = r1x1 + r2x2 + . . . + rkxk mod M. 

Der Beweis, dass diese Methode universell ist, wird auf die gleiche Weise konstruiert wie der Beweis der Matrixmethode. Sei x und y zwei verschiedene Schlüssel. Wir wollen zeigen, dass Prh (h (x) = h (y)) ≤ 1 / M ist. Da x! = Y, sollte es einen Fall geben, in dem ein Index i existiert, so dass xi! = Yi. Stellen Sie sich nun vor, Sie hätten zuerst alle Zufallszahlen rj für j! = I ausgewählt. Sei h '(x) = Pj6 = i rjxj. Wenn wir also ri wählen, erhalten wir h (x) = h '(x) + rixi. Dies bedeutet, dass wir genau dann einen Konflikt zwischen x und y haben

 h′(x) + rixi = h′(y) + riyi mod M, or equivalently when ri(xi − yi) = h′(y) − h′(x) mod M. 

Da M eine Primzahl ist, ist die Division durch einen Wert ungleich Null von mod M gültig (jede ganze Zahl von 1 bis M −1 hat ein multiplikatives inverses Modulo M), was bedeutet, dass es genau einen Wert ri modulo M gibt, für den die obige Gleichung gilt wahr, nämlich ri = (h '(y) - h' (x)) / (xi - yi) mod M. Somit ist die Wahrscheinlichkeit dieses Vorfalls genau 1 / M.

6.2 Andere Verwendungen von Hashing

Angenommen, wir haben eine lange Folge von Elementen und möchten sehen, wie viele verschiedene Elemente in der Liste enthalten sind. Gibt es eine gute Möglichkeit, dies zu tun?

Eine Möglichkeit besteht darin, eine Hash-Tabelle zu erstellen und dann die Sequenz einmal zu durchlaufen, indem nach jedem Element gesucht und dann eingefügt wird, wenn es nicht bereits in der Tabelle enthalten ist. Die Anzahl der einzelnen Elemente ist einfach die Anzahl der Einfügungen.

Und jetzt, was ist, wenn die Liste wirklich riesig ist und wir keinen Platz zum Speichern haben, aber eine ungefähre Antwort für uns geeignet ist. Stellen Sie sich zum Beispiel vor, wir sind ein Router und beobachten, wie viele Pakete übertragen werden, und wir möchten (ungefähr) sehen, wie viele verschiedene Quell-IP-Adressen vorhanden sind.

Hier ist eine gute Idee: Nehmen wir an, wir haben eine Hash-Funktion h, die sich wie eine Zufallsfunktion verhält, und stellen wir uns vor, dass h (x) eine reelle Zahl von 0 bis 1 ist. Wir können nur das Minimum verfolgen Der Hash-Wert wurde bisher erstellt (wir haben also überhaupt keine Tabelle). Wenn zum Beispiel die Schlüssel 3,10,3,3,12,10,12 und h (3) = 0,4, h (10) = 0,2, h (12) = 0,7 sind, erhalten wir 0, 2.

Tatsache ist, dass wenn wir in [0, 1] N Zufallszahlen auswählen, der erwartete Mindestwert 1 / (N + 1) ist. Darüber hinaus besteht eine gute Chance, dass es ziemlich nahe ist (wir können unsere Schätzung verbessern, indem wir mehrere Hash-Funktionen ausführen und den Median der Tiefs nehmen).

Frage: Warum eine Hash-Funktion verwenden und nicht jedes Mal eine Zufallszahl auswählen? Dies liegt daran, dass wir uns um die Anzahl der verschiedenen Elemente kümmern und nicht nur um die Gesamtzahl der Elemente (dieses Problem ist viel einfacher: Verwenden Sie einfach einen Zähler ...).

Freunde, war dieser Artikel hilfreich für Sie? Schreiben Sie in die Kommentare und nehmen Sie am Tag der offenen Tür teil , der am 25. April stattfinden wird.