Hallo lieber Leser! Ich präsentiere Ihnen die englische Übersetzung des Artikels „Physik, die nächste Grenze“ von Chris Hecker.

Ich, ein unerfahrener Java-Entwickler, war mit der Tatsache konfrontiert, dass die Materialien zum Erstellen einer physischen In-Game-Engine nur auf Englisch präsentiert werden. Daher wurde dieser Artikel übersetzt. Es werden drei weitere Artikel in der Reihe sein, ich werde sie so schnell wie möglich veröffentlichen. Viel Spaß beim Lesen!

Neue Grenzen in der Physik

Es besteht kein Zweifel, dass die Grafiken im Spiel von Jahr zu Jahr realistischer werden. Bereits heute erstellt jeder (oder zeigt zumindest Screenshots) 3D-Welten mit Texturkarten, und wenn genügend fleißige Leute zusammenkommen, um an einem Projekt zu arbeiten, kann jeder Entwickler Milliarden von Polygonen realistischer Texturen und Schatten pro Sekunde zeichnen. Was bleibt technisch noch zu tun, um ein Spiel auf hohem Niveau zu schaffen? Wird jeder Entwickler mit einer Kopie des Buches „Lernen, wie man 3D-Hardware in 21 Tagen verwendet“ ein wirklich beeindruckendes Spiel erstellen können?

Überhaupt nicht. Gehobene Entwickler werden die Messlatte für viele verschiedene Technologien (wie GUI-Komplexität, künstliche Intelligenz und Vernetzung) weiterhin höher legen. All dies ist natürlich sehr wichtig. Wir können keines von ihnen ernsthaft diskutieren, ohne Details anzugeben. Dennoch gibt es eine Technologie, die auf alles anwendbar ist und meiner Meinung nach in naher Zukunft zu einem entscheidenden Faktor werden wird: die Physik.

Betrachten Sie das folgende Beispiel: Erinnern Sie sich an diese riesigen Spinnräder in einem der frühen Levels von Duke Nukem 3D?



Abbildung 1. Screenshot aus dem Spiel "Duke Nukem 3D"

Stellen Sie sich vor, ihre Rotation würde nicht durch eine zyklische Animation beschrieben, sondern durch eine echte physische Engine. Plötzlich werden die Zahnräder zu mehr als einer Spieldekoration, so wie einer von ihnen vom vorgegebenen Winkel abweicht und den Korridor hinter Ihnen hinunter rollt, wie in den Indiana Jones-Filmen. Oder stellen Sie sich vor, dass ein Gerät, das von einem Raketenwerfer abgefeuert wurde, den Korridor entlang rollt und Ihren Freund vernichtet, der sich hinter Sie geschlichen hat, um Sie zu töten! Physische Motoren machen solche Situationen real.

Physische Simulation macht die Spielwelt ganz: Dank dieser Tatsache befindet sich „hier“ hier, wenn Sie verstehen, was ich meine. Jede Magie in den Grafiken der Welt erlaubt es dem Spieler nicht, in den Spielprozess einzutauchen, wenn er in einen anderen Spieler oder in die Wände des Levels eindringt oder wenn die Masse und der Moment der Masse nicht gefühlt werden. Die Animatoren von Disney empfanden dieses Gefühl der Massen als das, was gute Animation von schlechter Animation unterscheidet. Laut Frank Thomas und Ollie Johnston, dem epischen Buch Disney Animation: Die Illusion des Lebens, sollten sich Disney-Animatoren, die nur ein Poster im Studio aufhängen, immer fragen: „Gibt es viel Gewicht, Tiefe und Gleichgewicht in ihrer Zeichnung? ? "

Aber heute hat fast jedes Spiel eine Physik-Engine, oder? Zweifellos verhindert dies, dass Ihr Auto über den Rand der Spielwelt fällt. Dank dessen fliegen Ihre Charaktere beim Springen nicht in den Weltraum, und dies wirft Ihr Boot zur Seite, wenn eine Rakete in der Nähe explodiert. Die meisten physischen Engines in modernen Spielen sind jedoch ziemlich schwach. Sie haben nur die Aufgabe, das Auto davon abzuhalten, über den Rand der Welt zu fallen, aber ihre Fähigkeiten reichen nicht aus, um das Spiel auf ein neues Level zu heben - wo die Trümmer eines zerstörten Autos direkt auf der Strecke explodieren und eine Rolle von Wänden und anderen Autos verursachen können.

Andere physische Effekte, die oft ignoriert werden, sind: von einfachen Verdrehungseffekten infolge eines Tangentenschlags bis hin zu den Charakteren im Spiel, die im Gegensatz zu statisch animierten die Balance halten und sich bewegen. Ich glaube, dass viele Entwickler diese Möglichkeiten ignorieren, weil sie die Mathematik, die die Physik beschreibt, nicht verstehen oder zu beschäftigt waren, Textur-Maps zu erstellen, um sie zu lernen. Der Ansturm der Hardware für die Arbeit mit 3D wird sich um Letzteres kümmern, und ich beginne eine neue Artikelserie. Der erste Artikel wird sich um die Formalitäten kümmern. Am Ende unseres Zyklus können Sie selbst eine physische Engine erstellen, mit der sich die Spieler dank unglaublichen Realismus oder eines unterhaltsamen, aber anhaltenden Surrealismus vollständig in das Gameplay vertieft fühlen.

Achtung! Physik = Mathematik, um ein interessantes Projekt abzuschließen, müssen Sie beide verwenden. Bevor dies Sie abschreckt, möchte ich darauf hinweisen, dass die Mathematik, die die Physik beschreibt, nicht nur elegant und schön ist, sondern auch einen angewandten Charakter hat. Das heißt, es ist keine abstrakte Mathematik für Mathematik. Jede Gleichung, die wir verwenden, hat eine echte physikalische Bedeutung. Wir erstellen Gleichungen aus einem physikalischen Modell und im Gegenzug sagen uns die Gleichungen, wie sich das Modell zeitlich verhält.

Großartiges Unternehmen

Die Physik ist ein weites wissenschaftliches Gebiet. Aber wir sind wirklich interessiert an seinem kleinen Abschnitt namens "Dynamik", genauer gesagt "Dynamik von Festkörpern". Die Dynamik kann anhand eines verwandten Abschnitts definiert werden - der Kinematik (der Doktrin der Bewegung in der Zeit). Die Kinematik konzentriert sich nicht darauf, was die Bewegung verursacht oder wie die Körper dort gelandet sind, wo sie sich befinden, sondern beschreibt lediglich die Bewegung. Im Gegensatz dazu beschreibt die Dynamik die Kräfte und Massen, die dazu beitragen, dass sich die Werte der Kinematik im Laufe der Zeit ändern. Wie weit der Baseballball fliegen wird, wenn die Flugzeit 10 Sekunden und seine Anfangsgeschwindigkeit 50 Kilometer / Stunde beträgt und die Flugbahn - eine gerade Linie - ein kinematisches Problem ist; Wie weit der Baseballball im Gravitationsfeld der Erde fliegen wird, wenn ich ihn mit einem Schläger treffe - das ist ein dynamisches Problem.

Der Teil der Dynamik, der Volumenkörper beschreibt, bezieht sich auf die Einschränkungen, die wir für simulierte Objekte hinzufügen. Die Form eines festen Körpers ändert sich während der Simulation nicht - der Körper ist eher aus Holz oder Metall als aus Gelee. Wir können zum Beispiel artikulierte Figuren einer Person erstellen, indem wir jeden Teil der Figur aus einem festen Körper konstruieren und Bänder zwischen ihnen erstellen. Wir rechnen jedoch nicht damit, dass sich die Knochen unter Stress oder ähnlichen Effekten verbiegen. Dadurch können wir unsere Gleichungen vereinfachen, ohne die Qualität des interessanten dynamischen Verhaltens von Körpern zu verlieren.

Obwohl wir einen so kleinen Teil der Dynamik betrachten werden, erfordert die Dynamik eines starren Körpers eine Reihe von Artikeln, um die Essenz zu erklären. Wir beginnen unsere Reise mit dem Studium der Grundlagen der Computerprogrammierung, um die Bewegung eines ebenen starren Körpers unter Krafteinwirkung zu beschreiben. Ich wiederhole beharrlich die „Computerprogrammierung“, da wir zusätzlich zu den Gleichungen, die wir für Kinematik und Dynamik schreiben, auch lernen werden, diese Gleichungen mithilfe von Berechnungen mit Gleitkommazahlen zu lösen, was für jeden Programmierer von entscheidender Bedeutung ist. Ich sage "flach fest", weil wir uns im nächsten Artikel und darüber hinaus nur mit der zweidimensionalen Welt befassen werden. Die Prinzipien - und tatsächlich mehr als nur Gleichungen - können auch auf die dreidimensionale Welt übertragen werden, aber in der zweidimensionalen Welt ist definitiv alles viel einfacher. Deshalb werden wir dort studieren, bis wir uns sicher fühlen, in den dreidimensionalen Raum einzutreten. In zukünftigen Artikeln werden wir lernen, die Wirkung der Rotation, die Verarbeitung von Körperkontakten und natürlich die Vorgehensweise in einer dreidimensionalen Welt zu beschreiben. Nun, genug Worte! Fangen wir an!

Arbeiten Sie mit einem Derivat

Dies mag Sie überraschen, aber Sie können ein Objekt wirklich nicht bewegen, indem Sie es einfach drücken. Ich weiß, du denkst, ich liege falsch darin, mir das Gegenteil zu beweisen, indem ich dieses Magazin in den Müll wirf, weil ich so einen Unsinn geschrieben habe, aber es ist wahr! Nur Druck auf ein Magazin auszuüben, wirkt sich niemals direkt auf seine Position im Weltraum aus. Tatsächlich wirkt sich der Druck nicht einmal direkt auf die Geschwindigkeit aus. Was Druck tatsächlich beeinflusst, ist die Beschleunigung der Zeitschrift, und tatsächlich ist es eine der wichtigsten Schlussfolgerungen in der Geschichte der Wissenschaft.

Um diese Tatsache zu nutzen, um etwas Interessantes zu tun, müssen wir zuerst über die Beziehung der Position des Körpers zu Geschwindigkeit und Beschleunigung sprechen. Tatsächlich sind alle diese Werte sehr eng miteinander verbunden (wie Sie wahrscheinlich wissen): Geschwindigkeit ist ein Indikator für Änderungen der Koordinaten des Körpers im Laufe der Zeit, und Beschleunigung ist ein Indikator für Änderungen der Geschwindigkeit. Das Hauptwerkzeug zur Untersuchung von Änderungen dieser Größen im Zeitverlauf ist die Differentialrechnung. Wenn Sie das verstehen, fahren wir fort. Ich nehme an, Sie sind gut in Mathe. Wir werden nur einfache Skalar- und Vektorberechnungen (Ableitungen und Integrale) verwenden, aber es ist nicht überflüssig, wenn Sie mit der Mathematik als Ganzes vertraut sind. Als Referenz: Mein Lieblingsbuch über Computer ist Calculus with Analytic Geometry von Thomas und Finney.

Koordinate, Geschwindigkeit und Beschleunigung sind Kinematiken, die in diesem Artikel behandelt werden. Die Position eines Festkörpers in einer zweidimensionalen Welt ist offensichtlich ein Koordinatenpaar X und Y, die die Koordinaten des Raums eines bestimmten Punktes des Körpers bezeichnen. Die Ableitung für den Koordinatenvektor ist der Geschwindigkeitsvektor und zeigt uns, in welche Richtung sich der Punkt bewegt (und der Körper, wenn wir die Rotation ignorieren, die gerade stattfindet) und wie schnell er sich bewegt. Die Vektorrechnung ist nur die Skalarrechnung jedes Elements des Vektors, daher ist die Ableitung der X-Koordinate die Körpergeschwindigkeit in Bezug auf X und so weiter. Wir führen die folgende Notation ein. Die Koordinate des Körpers sei der Vektor r und die Geschwindigkeit der Vektor v oder der Vektor r mit einer Primzahl. Wir bekommen die Gleichung:

$$

$${{dx} \ over {dt}} = v = r '$$

Gleichung 1

Wenn wir den Geschwindigkeitsvektor in Bezug auf die Zeit differenzieren, zeigt dies, wie sich der Koordinatenvektor mit der Zeit ändert. Die Beschleunigung wird analog bestimmt. Dies ist die erste Ableitung der Geschwindigkeit oder die zweite Ableitung des Koordinatenvektors:

$$

$${{d ^ 2 r} \ über {dt ^ 2}} = r '' = {{dr '} \ über {dt}} = {{dv} \ über {dt}} = v' = a$$

Gleichung 2

Das Integral der Beschleunigung gibt uns Geschwindigkeit, und wenn wir die Beschleunigung zweimal integrieren, erhalten wir die Koordinate.

Diese Beziehungen in der Kinematik zeigen, dass wir die Beschleunigung eines Objekts finden und im Laufe der Zeit integrieren können, um die Geschwindigkeit und Koordinate zu erhalten. Wie wir später sehen werden, werden wir uns mehrmals der Integration in unseren Simulationscode zuwenden und für jeden Frame eine neue Position für unseren Volumenkörper berechnen. Hurra Animation!

Hier ist ein einfaches Beispiel für eine eindimensionale Welt, die wir analytisch integrieren können. Lassen Sie uns zustimmen, dass wir die Koordinatenänderung vom Ende des letzten Rahmens bis zum Zeitpunkt des aktuellen Rahmens ermitteln möchten, um die aktuelle Position zu zeichnen. Als nächstes sagen wir, dass die Beschleunigung unseres Festkörpers gleich 5 willkürliche Einheiten / Sekunde ^ 2 war. Wir werden die seit dem Ende des letzten Frames verstrichene Zeit als Variable t (im Integrationselement dt) verwenden.

$$

$$v (t) = ∫adt = ∫5dt = 5t + C$$

Gleichung 3

Die obigen Gleichungen zeigen, dass die Geschwindigkeit eine Funktion der Zeit ist, die seit dem letzten Frame vergangen ist. Wir fanden die Integrationskonstante C, die gleich der Anfangsgeschwindigkeit zu Beginn der Integrationsperiode ist (bei t = 0).

$$

$$v (0) = 5 (0) + C$$

$$

$$v_0 = {C}$$

Gleichung 4

$$

$$v (t) = 5t + v_0 {}$$

Jetzt integrieren wir unsere Geschwindigkeitsgleichung, um die Koordinate zu finden (vergessen Sie auch hier nicht die Integrationskonstante):

$$

$$r (t) = ∫v (t) dt = ∫5t + v_0 dt = {{5} \ über {2}} t ^ 2 + v_0 t + r_0$$

Gleichung 5

Basierend auf Gleichung 5 können wir die aktuelle Position nur durch eine gegebene Beschleunigung finden, wenn wir die anfängliche Koordinate und Geschwindigkeit (die wir aus dem letzten Frame nehmen werden) und die verstrichene Zeit kennen. Die Eingangsvariable ist die Zeit und der Wert der Funktion ist die aktuelle Position. Wir werden auch die Zeit in Gleichung 4 angeben, um die Endgeschwindigkeit zu berechnen, damit wir diese als Anfangsbedingung für den nächsten Rahmen verwenden können.

Möge die Macht mit dir sein

Jetzt haben wir die Erkenntnis, dass wir die Beschleunigung richtig einstellen müssen, um die Kinematikgleichungen zu integrieren, um die Animation zu erhalten. Der Ausgang der Lautsprecher auf der Bühne. Erinnern Sie sich, wie gesagt, dass Sie durch Drücken auf etwas direkt nur die Beschleunigung des Körpers beeinflussen? Nun, „Druck ausüben“ ist nur ein Euphemismus für den Ausdruck „Kraft anwenden“ - eine der beiden Schlüsselvariablen in der Dynamik - und jetzt können wir uns an Newton wenden, um herauszufinden, wie Kräfte die Beschleunigung beeinflussen. Newtons zweites Gesetz verbindet die Kraft F mit der Ableitung der Masse - der zweiten Größe der Dynamik - mal der Geschwindigkeit. Das Produkt aus Masse und Geschwindigkeit wird als "Impuls des Körpers" bezeichnet, bezeichnet mit p:

$$

$$F = p '= {{dp} \ über {dt}} = {{d (mv)} \ über {dt}} = mv' = ma$$

Gleichung 6

Die Masse ist eine Konstante für die Geschwindigkeiten, mit denen wir jetzt arbeiten. Dies folgt aus der Ableitung in Gleichung 6, und wir haben die bekannte Gleichung F = ma erhalten (obwohl ich sicher bin, dass Newton die Kraft ursprünglich durch die Ableitung des Impulses bestimmt hat).

Wenn wir uns nur mit materiellen Punkten befassen, ist Gleichung 6 das, was wir in der Dynamik brauchen. Für eine gegebene Kraft eines gegebenen Materialpunktes wird die Beschleunigung durch Teilen der Kraft durch Masse gefunden. Dies gibt uns eine Beschleunigung, die hilft, die Bewegungsgleichung aus dem obigen Beispiel zu lösen. Trotzdem haben wir es mit Festkörpern zu tun, deren Masse über einen bestimmten Bereich verteilt ist (Volumen, wenn es um die dreidimensionale Welt geht), also müssen wir noch arbeiten.

Betrachten Sie zunächst einen Festkörper als eine Menge von Punktmassen. Wir definieren den Gesamtimpuls pT für einen Festkörper als die Summe der Impulse aller Punkte, aus denen der Körper besteht (ich verwende die obere Indizierung, weil ich klarer zeigen möchte, welche quantitativen Werte zu diesen Punkten gehören):

$$

$$p ^ T = \ sum_ {i} {m ^ i v ^ i}$$

Gleichung 7

Wir können die Analyse der Dynamik eines starren Körpers erheblich vereinfachen, indem wir das Konzept des Massenschwerpunkts (CM) einführen. Ein auf den Massenmittelpunkt gerichteter Vektor ist eine lineare Summe von Vektoren, die von allen Massenpunkten eines festen Körpers gerichtet sind, geteilt durch die Masse des gesamten Körpers, M:

$$

$$r ^ {CM} = {\ sum_ {i} {m ^ i r ^ i} \ über {M}}$$

Gleichung 8

Unter Verwendung der Definition des Massenschwerpunkts können wir Gleichung 7 vereinfachen, indem wir beide Seiten von Gleichung 8 mit M multiplizieren, sie differenzieren und dann das Ergebnis in Gleichung 7 einsetzen:

$$

$${{d (Mr ^ {CM})} \ über {dt}} = {\ sum_ {i} {} {{d (m ^ ir ^ i) \ über dt}}} = {\ sum_ {i} {} {m ^ iv ^ i}} = p ^ T$$

Gleichung 9

Die rechte Seite von Gleichung 9 ist der in Gleichung 7 definierte Gesamtimpuls. Schauen wir uns nun die linke Seite der Gleichung an: Dies ist die Geschwindigkeit im Massenmittelpunkt multipliziert mit der Masse des gesamten Körpers. Bewegen Sie die rechte Seite nach links und erhalten Sie:

$$

$$p ^ T = {{d (Mr ^ {CM})} \ over {dt}} = Mv ^ {CM}$$

Gleichung 10

Aus Gleichung 10 folgt, dass der lineare Impuls gleich der Gesamtmasse multipliziert mit der vom Massenmittelpunkt gerichteten Geschwindigkeit ist, so dass es nicht erforderlich ist, in Gleichung 7 zu summieren, um den Impuls zu finden, wenn wir die Masse des Körpers und die Richtung des Geschwindigkeitsvektors des Massenschwerpunkts kennen. Ferner finden alle Endergebnisse der Berechnungen die Integrale für den gesamten Körper, aber der Schwerpunkt existiert und vereinfacht die Bestimmung des Gesamtimpulses aus Gleichung 10 erheblich, sodass wir uns keine Sorgen machen können - um den linearen Impuls zu finden, können wir den Körper als Materialpunkt mit gegebener Geschwindigkeit und Masse betrachten.

In Analogie dazu ist die Gesamtkraft eine Ableitung des Gesamtimpulses, sodass das Konzept des Massenschwerpunkts verwendet werden kann, um die Kraftgleichung zu vereinfachen:

$$

$$F ^ T = p ^ T = Mv '^ {CM} = Ma ^ {CM}$$

Gleichung 11

Kurz gesagt, aus Gleichung 11 folgt, dass wir alle Kräfte betrachten können, die mit einem Festkörper interagieren, als ob ihr Summenvektor einen Einfluss auf den Punkt des Massenschwerpunkts hätte, der die Masse des gesamten Körpers enthält. Wir teilen die Kraft (Schwerkraft ablesen) durch M, um die Beschleunigung des Massenschwerpunkts zu ermitteln, und integrieren dann die Beschleunigung zeitlich, um die Geschwindigkeit und Koordinate des Körpers zu erhalten. Weil Wir ignorieren die Auswirkungen der Rotation bis zum nächsten Artikel. Wir haben bereits alle Gleichungen, die wir zur Beschreibung der Dynamik eines starren Körpers benötigen. Es ist zu beachten, dass Gleichung 11 keine Informationen darüber enthält, wohin die auf den Körper ausgeübten Kräfte gerichtet sind. Dies wird angezeigt, wenn wir uns mit dem linearen Impuls und dem Massenschwerpunkt befassen und nur Kräfte auf das CM ausüben, um die Beschleunigung des Massenschwerpunkts zu ermitteln. Wenn wir im nächsten Artikel die Rotation des Körpers unter dem Einfluss dieser Kräfte berechnen, werden wir sehen, wie die Koordinate der Krafteinwirkung verwendet wird.

Ode an die Freude

In diesem Stadium können wir ein weiteres Beispiel für die analytische Integration betrachten, indem wir Gleichung 11 verwenden, um die Beschleunigung des Massenschwerpunkts anstelle eines willkürlich gewählten Werts = 5 zu ermitteln. Dennoch stehen wir vor einem ernsthaften Problem, da die analytische Integration normalerweise keinen angewendeten Wert hat, weil Da es zu kompliziert ist, konzentrieren wir uns auf die sogenannte numerische Integration gewöhnlicher Differentialgleichungen (ODEs). Wow, das klingt nach echter Mathematik! Sobald Sie dies gelernt haben, wird es Zeit, die Messlatte höher zu legen. Glücklicherweise ist die numerische Integration von ODEs nicht so schwierig, wie es auf den ersten Blick erscheinen mag! Um zu verstehen, was dies bedeutet, bewegen wir uns von Worten zu Taten!

Eine Differentialgleichung ist also eine Gleichung, die neben der Funktion selbst Ableitungen abhängiger Größen, unabhängige Variablen und Parameter enthält. Dies ist ausführlich, aber hier ist ein Beispiel für eine zeitlich veränderliche Kraft in einer eindimensionalen Welt: F = 2t, F ist eine abhängige Größe und t ist unabhängig. Der Wert von F wird nur durch F bestimmt. Lassen Sie die Kraftgleichung nur von der Geschwindigkeit unseres Körpers abhängen.Die Kraft des Luftwiderstands nimmt mit zunehmender Geschwindigkeit des Flugzeugs zu. Kehren wir zum Beispiel in der eindimensionalen Welt zurück. Was ist, wenn F = -v bedeutet, dass die Reibungskraft unseren Körper proportional zur Geschwindigkeit verlangsamt? Wir haben ein Problem, weil wir die Gleichung wie folgt lösen: F = ma = -v und dividiert durch m erhalten wir (denken Sie daran, dass die Beschleunigung eine Ableitung der Geschwindigkeit ist):

$$

$$a = {{dv}\over {dt}} = {-v\over m}$$

Gleichung 12

Diese Differentialgleichung (die Geschwindigkeitsgleichung enthält die Geschwindigkeitsableitung in Gleichung 12) wird als gewöhnliche Differentialgleichung bezeichnet, da sie nur gewöhnliche Ableitungen abhängiger Größen enthält (im Gegensatz zu partiellen Ableitungen, die partielle Differentialgleichungen [PDEs] bilden, über die wir nicht sprechen wir werden reden).

Kommen wir nun zum nächsten Teil unseres Satzes: Integration. Wie haben wir zuvor dv / dt integriert, um v in den Bedingungen dieser Gleichung zu finden?

Dies wird unglaublich erscheinen, aber fast jede Gleichung in der Physik ist differentiell, so dass ODEs gut untersucht wurden. Differentialgleichungen sind in der Physik so häufig anzutreffen, weil die Änderungsrate einer quantitativen Größe häufig von der Größe selbst abhängt. Zum Beispiel haben wir bereits festgestellt, dass das Bremsen (das Ausmaß einer Geschwindigkeitsänderung), einschließlich der Geschwindigkeit des Luftwiderstands, von der Geschwindigkeit abhängt. Weitere Beispiele aus der Physik: Abkühlung (die Wärmeverlustrate hängt von der aktuellen Temperatur ab) und radioaktiver Zerfall (Zerfallsrate hängt davon ab, wie viel radioaktives Material vorhanden ist).

Das letzte Wort in unserer Phrase - numerisch - ist unsere Erlösung. Ich sage das, weil die Theorie der analytischen Integration von Differentialgleichungen, selbst der einfachsten, riesig und ziemlich verwirrend ist. Ironischerweise ist die Integration von ODEs mit numerischen Computermethoden relativ einfach zu verstehen. Als nächstes werde ich einen einfachen numerischen Integrator beschreiben, der auf der Euler-Methode basiert, und ihn im nächsten Artikel verfeinern.

Fast alle numerischen Integratoren, aber kein anderer, der so explizit ist wie die Euler-Methode, basieren einfach auf der alten Definition der Berechnung durch die erste Ableitung der Neigung: dy / dx bestimmt die Steigung von y in Abhängigkeit von x. Wenn wir zum Beispiel die lineare Gleichung y = 5x haben, bedeutet dy / dx = 5, dass die Steigung für jedes x eine Konstante von 5 ist, und wie Sie annehmen können, ist dies eine gerade Linie. Ein etwas schwierigeres Beispiel ist die Parabel y = x2. In diesem Fall ist dy / dx = 2x, und dies ist eine Funktion zum Bestimmen der neuen Neigung für jede x-Koordinate. Ich habe y = x2 in Abbildung 2 dargestellt: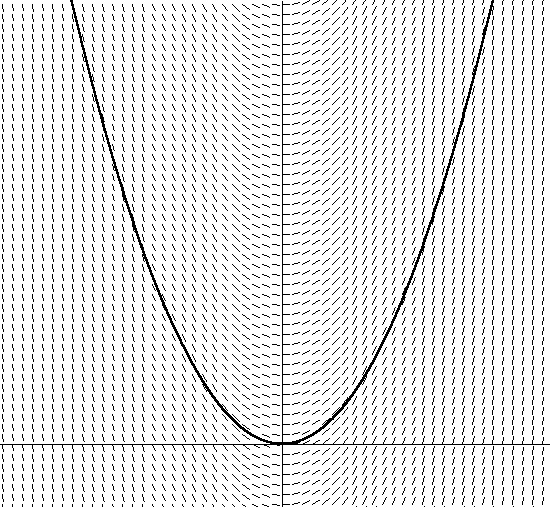



Abbildung 2. y = x2

Zusätzlich habe ich die Richtung des Vektors schräg geschlüpft, indem ich die Gleichung dy / dx = 2x + C für alle x gelöst habe. Beachten Sie, dass der Winkel des geneigten Vektors an dieser Stelle gleich der Tangente des Tangentenwinkels ist. Beachten Sie auch, dass es viele verschiedene Parabeln gibt, die den Winkel des Tangentensatzes erfüllen und sich nur in einer Verschiebung entlang der y-Achse unterscheiden. Jede dieser Parabeln wird unter Verwendung verschiedener Integrationskonstanten erhalten, die in der Gleichung dy / dx = 2x + C enthalten sind. Die abgebildete Parabel hat eine Integrationskonstante von 0. Wenn ich eine andere Konstante wähle, zum Beispiel 1, erhalte ich die Gleichung y = 2x + 1. Dies bedeutet, dass es eine ähnliche Parabel mit einer Verschiebung von 1 Einheit entlang der y-Achse gibt.

Denken Sie nun an die Tatsache, dass Sie, wenn Sie das durch eine Parabel definierte Vektorfeld in Abbildung 2 nicht kennen, einfach in einer Pfütze sitzen. Wenn Sie also die Tangentengleichung lösen möchten, müssen Sie nur an jedem Punkt der Richtung des Vektors folgen und die Richtung entsprechend der Richtungsänderung des Vektorfelds ändern. Sie werden überrascht sein, dass Sie nach einiger Zeit feststellen werden, dass Sie sich auf einer parabolischen Flugbahn (oder entlang eines Abschnitts der Parabel) bewegen, je nachdem, wo Sie begonnen haben. Ohne es zu merken, haben Sie die Gleichung des Vektorfeldes integriert. Sie haben eine bestimmte Parabel gefunden (abhängig davon, wo Sie begonnen haben oder unter den Anfangsbedingungen), indem Sie nur die Ableitungsgleichung verwendet haben (Berechnung von dy / dx, wenn Sie sich im Vektorfeld bewegen).

Dasselbe für eine echte Differentialgleichung zu tun, ist ebenfalls einfach. Für eine Differentialgleichung vom Typ dy / dx = f (x, y) beschreibt das Finden der Ableitung dy / dx als Tangente an f (x, y) den Neigungswinkel der Tangente für jede Koordinate im x, y-Diagramm. Wenn Sie ein Vektorfeld zeichnen, das durch dy / dx = f (x, y) gegeben ist, können Sie dies analog zu einer Parabel verfolgen, indem Sie die Ableitung an jedem Punkt finden und in diese Richtung folgen. Abbildung 2 zeigt ein Vektorfeld für Gleichung 12, unsere Gleichung für den Luftwiderstand, mit Geschwindigkeit entlang der vertikalen Achse und Zeit entlang der Horizontalen (ich habe für diesen Graphen willkürlich m = 1 gewählt).



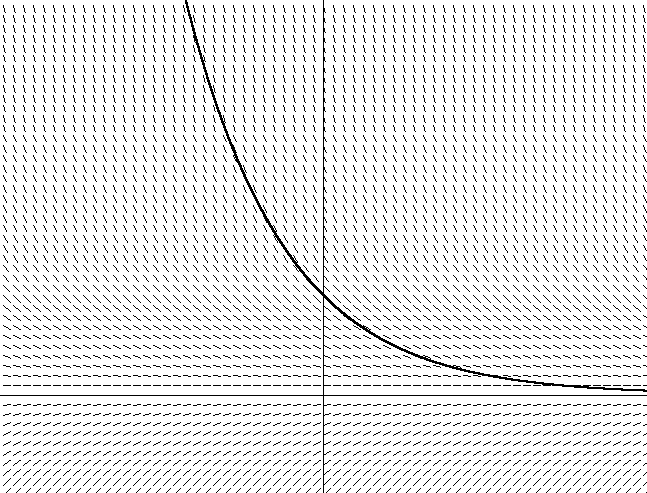Abbildung 3. dv / dt = -v / m

Es zeigt auch eine der vielen möglichen Kurven. Möglicherweise stellen Sie fest, dass bei Auswahl der Startposition im Diagramm (die von der Anfangsgeschwindigkeit in der Gleichung abhängt) die Geschwindigkeit im Laufe der Zeit gegen Null tendiert, da die Reibungskraft den Körper verlangsamt. Sie können auch sehen, wie die Geschwindigkeitsabnahme vom aktuellen Geschwindigkeitswert abhängt. Je schneller Sie sich bewegen, desto schneller nimmt sie ab. Dies wird deutlich, wenn dasselbe aus Gleichung 12 folgt.

Die numerische Integration ähnelt der in der Tabelle beschriebenen. Der Euler-Algorithmus für die numerische Integration folgt einfach dem Vektorfeld gemäß der Anfangsposition, indem er die Ableitung der Gleichung (-v / m für unser Beispiel mit der Reibungskraft) findet, um die Steigung am aktuellen Punkt zu bestimmen, und bewegt sich dann einfach schrittweise vorwärts, abhängig von unveränderter Wert von h entlang der Steigung. Dann wird eine neue Position berechnet, um die neue Steigung nach einem bestimmten Zeitintervall zu bestimmen:

$$

$$y_{n+1} ≈ y_{ n } + {h(dy_{ n })\over dx}$$

Genauer gesagt für unsere Luftwiderstandsgleichung:

$$

$$v_{ n+1 } ≈v_{ n }+{h( -v_{n})\over m}$$

Offensichtlich ergibt die Euler-Methode bei jedem Zeitschritt einen kleinen Fehler, da sich der reale Geschwindigkeitsvektor (und damit die Lösungskurve) an jedem Punkt mit einer Abweichung biegt und der Euler-Algorithmus geringfügig vom Neigungswinkel abweicht. Wenn jedoch der Zeitschritt h eher kleine Größen sind, tendiert der Fehler gegen Null. Wir werden dies in Zukunft genauer diskutieren.

Dies ist alles, was Sie über die numerische Integration mit der Euler-Methode wissen müssen. Sie können sich fragen, wie wir die Geschwindigkeit integrieren, um die Koordinate zu erhalten. Wir verwenden einfach die Euler-Methode erneut, um dr / dt = v zu integrieren, genauso wie wir dv / dt = a analog integriert haben. Wir erhalten zwei zusammenhängende Differentialgleichungen (eine weitere von unserem Sieg):

$$

$$v_{n+1} ≈ v_n+hv'=v_n+{h F_n\over M }$$

$$

$$r_{ n+1 } = r_n + hr_n'= r_n+hv_n$$

Dies gibt uns einen alternativen Algorithmus zur Berechnung der Koordinate nach der Einwirkung einer willkürlich auf unser Objekt ausgeübten Kraft (die von der Geschwindigkeit, wie wir sie gesehen haben, der Zeit oder sogar der Position unseres Körpers und anderer Körper oder auf einmal abhängen kann!). Bei der Euler-Methode spielt es keine Rolle, wie die aufgebrachte Kraft aussieht, da Sie sie jederzeit berechnen können. Euler interessiert sich für das Ausmaß der Kraftwirkung auf die Masse als geneigt, und das war's.
Ich habe keinen Platz mehr, daher kann ich keine Links mehr bereitstellen. Das nächste Mal werde ich verschiedene wundervolle Bücher beraten und herausfinden, wie die Rotation von Festkörpern berechnet werden kann.

Und obwohl sein Körper nicht so solide ist, wie wir es gerne hätten, hat Chris Hecker eine dynamische Persönlichkeit. Wenn Sie Gewalt anwenden, wird er eine E-Mail an checker@bix.com senden.

Anmerkungen des Übersetzers: Hier wird ein Wortspiel vorgestellt, das Thema des Artikels und sein Inhalt werden abgespielt.

PS Der Autor der Übersetzung bedankt sich ganz besonders bei den Nutzern von berez und MarazmDed für die Bearbeitung der Übersetzung. Vielen Dank!