Unterscheiden Sie Zeichen von Müll: So erstellen Sie robuste neuronale Netzwerkmodelle in OCR-Aufgaben

In jüngster Zeit setzen wir in der ABBYY-Erkennungsgruppe zunehmend neuronale Netze für verschiedene Aufgaben ein. Sehr gut haben sie sich vor allem für komplexe Schreibweisen bewährt. In früheren Beiträgen haben wir darüber gesprochen, wie wir neuronale Netze verwenden, um japanische, chinesische und koreanische Skripte zu erkennen.

Beitrag über die Erkennung japanischer und chinesischer Schriftzeichen
Post zur Erkennung koreanischer Zeichen

In beiden Fällen haben wir neuronale Netze verwendet, um die Klassifizierungsmethode für ein einzelnes Symbol vollständig zu ersetzen. Alle Ansätze umfassten viele verschiedene Netzwerke, und einige der Aufgaben umfassten die Notwendigkeit, Bilder, die keine Symbole sind, angemessen zu bearbeiten. Das Modell in diesen Situationen sollte irgendwie signalisieren, dass wir kein Symbol sind. Heute werden wir nur darüber sprechen, warum dies im Prinzip notwendig sein kann und über Ansätze, mit denen der gewünschte Effekt erzielt werden kann.

Motivation

Was ist das Problem? Warum an Bildern arbeiten, die keine separaten Zeichen sind? Es scheint, dass Sie ein Fragment einer Zeichenfolge in Zeichen unterteilen, alle klassifizieren und das Ergebnis daraus sammeln können, wie beispielsweise im folgenden Bild.



Ja, speziell in diesem Fall kann dies wirklich getan werden. Leider ist die reale Welt viel komplizierter, und in der Praxis muss man sich beim Erkennen mit geometrischen Verzerrungen, Unschärfen, Kaffeeflecken und anderen Schwierigkeiten auseinandersetzen.

Infolgedessen müssen Sie häufig mit solchen Fragmenten arbeiten:



Ich denke, es ist für alle offensichtlich, wo das Problem liegt. Nach einem solchen Bild eines Fragments ist es nicht so einfach, es eindeutig in separate Symbole zu unterteilen, um sie einzeln zu erkennen. Wir müssen eine Reihe von Hypothesen aufstellen, wo sich die Grenzen zwischen den Zeichen befinden und wo sich die Zeichen selbst befinden. Hierfür verwenden wir den sogenannten Linear Division Graph (GLD). Im obigen Bild ist dieses Diagramm unten dargestellt: Die grünen Segmente sind die Bögen der konstruierten GLD, dh die Hypothesen darüber, wo sich die einzelnen Symbole befinden.

Somit sind einige der Bilder, für die das Einzelzeichenerkennungsmodul gestartet wird, tatsächlich keine Einzelzeichen, sondern Segmentierungsfehler. Und dasselbe Modul sollte signalisieren, dass es höchstwahrscheinlich kein Symbol davor ist, was für alle Erkennungsoptionen ein geringes Vertrauen zurückgibt. Und wenn dies nicht geschieht, kann am Ende die falsche Option zum Segmentieren dieses Fragments nach Symbolen gewählt werden, was die Anzahl der linearen Teilungsfehler erheblich erhöht.

Zusätzlich zu Segmentierungsfehlern muss das Modell auch gegen A-priori-Müll von der Seite resistent sein. Hier können beispielsweise auch solche Bilder gesendet werden, um ein einzelnes Zeichen zu erkennen:



Wenn Sie solche Bilder einfach in separate Zeichen klassifizieren, fallen die Klassifizierungsergebnisse in die Erkennungsergebnisse. Darüber hinaus sind diese Bilder lediglich Artefakte des Binarisierungsalgorithmus, nichts sollte ihnen im Endergebnis entsprechen. Auch für sie müssen Sie in der Lage sein, ein geringes Vertrauen in die Klassifizierung zurückzugeben.

Alle ähnlichen Bilder: Segmentierungsfehler, a priori Müll usw. Wir werden im Folgenden negative Beispiele genannt. Bilder von realen Symbolen werden als positive Beispiele bezeichnet.

Das Problem des neuronalen Netzwerkansatzes

Erinnern wir uns nun daran, wie ein normales neuronales Netzwerk funktioniert, um einzelne Zeichen zu erkennen. Normalerweise ist dies eine Art Faltungsschicht und vollständig verbundene Schicht, mit deren Hilfe der Vektor der Wahrscheinlichkeiten der Zugehörigkeit zu jeder bestimmten Klasse aus dem Eingabebild gebildet wird.



Darüber hinaus stimmt die Anzahl der Klassen mit der Größe des Alphabets überein. Während des Trainings des neuronalen Netzwerks werden Bilder von realen Symbolen bereitgestellt und gelehrt, um eine hohe Wahrscheinlichkeit für die richtige Symbolklasse zurückzugeben.

Und was passiert, wenn ein neuronales Netzwerk mit Segmentierungsfehlern und a priori Müll gespeist wird? Rein theoretisch kann alles passieren, weil das Netzwerk solche Bilder im Lernprozess überhaupt nicht gesehen hat. Bei einigen Bildern kann es ein Glück sein, und das Netzwerk gibt für alle Klassen eine geringe Wahrscheinlichkeit zurück. In einigen Fällen kann das Netzwerk jedoch beginnen, im Müll am Eingang nach den bekannten Umrissen eines bestimmten Symbols zu suchen, beispielsweise nach dem Symbol „A“, und es mit einer Wahrscheinlichkeit von 0,99 erkennen.

In der Praxis führte die Verwendung der groben Wahrscheinlichkeit aus der Ausgabe des Netzwerks zum Auftreten einer großen Anzahl von Segmentierungsfehlern, als wir beispielsweise an einem neuronalen Netzwerkmodell für japanische und chinesische Schrift arbeiteten. Und trotz der Tatsache, dass das symbolische Modell auf der Basis von Bildern sehr gut funktionierte, war es nicht möglich, es in den vollständigen Erkennungsalgorithmus zu integrieren.

Jemand könnte fragen: Warum genau bei neuronalen Netzen tritt ein solches Problem auf? Warum funktionierten die Attributklassifikatoren nicht auf die gleiche Weise, weil sie auch anhand von Bildern studierten, was bedeutet, dass es im Lernprozess keine negativen Beispiele gab?

Der grundlegende Unterschied besteht meiner Meinung nach darin, wie genau Zeichen von Symbolbildern unterschieden werden. Im Fall des üblichen Klassifikators schreibt eine Person selbst vor, wie sie extrahiert werden sollen, wobei sie sich an einigen Kenntnissen ihres Geräts orientiert. Bei einem neuronalen Netzwerk ist die Merkmalsextraktion ebenfalls ein trainierter Teil des Modells: Sie sind so konfiguriert, dass Zeichen aus verschiedenen Klassen optimal unterschieden werden können. In der Praxis stellt sich heraus, dass die von einer Person beschriebenen Merkmale gegenüber Bildern, die keine Symbole sind, widerstandsfähiger sind: Es ist weniger wahrscheinlich, dass sie mit Bildern realer Symbole identisch sind, was bedeutet, dass ihnen ein niedrigerer Vertrauenswert zurückgegeben werden kann.

Verbesserung der Modellstabilität durch Center Loss

Weil Unserem Verdacht zufolge bestand das Problem darin, wie das neuronale Netzwerk Zeichen auswählt. Wir beschlossen, diesen bestimmten Teil zu verbessern, dh zu lernen, wie einige „gute“ Zeichen hervorgehoben werden. Beim Deep Learning gibt es einen separaten Abschnitt, der diesem Thema gewidmet ist und als „Repräsentationslernen“ bezeichnet wird. Wir haben uns entschlossen, verschiedene erfolgreiche Ansätze in diesem Bereich auszuprobieren. Die meisten Lösungen wurden für das Training von Repräsentationen bei Gesichtserkennungsproblemen vorgeschlagen.

Der im Artikel „ Ein diskriminativer Lernansatz für die Gesichtserkennung “ beschriebene Ansatz schien recht gut zu sein. Die Hauptidee der Autoren: Hinzufügen eines zusätzlichen Begriffs zur Verlustfunktion, wodurch der euklidische Abstand im Merkmalsraum zwischen Elementen derselben Klasse verringert wird.



Für verschiedene Werte des Gewichts dieses Terms in der allgemeinen Verlustfunktion kann man verschiedene Bilder in den Attributräumen erhalten:



Diese Abbildung zeigt die Verteilung der Elemente einer Testprobe in einem zweidimensionalen Attributraum. Das Problem der Klassifizierung handschriftlicher Zahlen wird berücksichtigt (Beispiel MNIST).

Eine der wichtigen Eigenschaften, die von den Autoren angegeben wurde: eine Erhöhung der Generalisierungsfähigkeit der erhaltenen Merkmale für Personen, die nicht im Trainingssatz waren. Die Gesichter einiger Leute befanden sich immer noch in der Nähe, und die Gesichter verschiedener Leute waren weit voneinander entfernt.

Wir haben uns entschlossen zu prüfen, ob eine ähnliche Eigenschaft für die Zeichenauswahl erhalten bleibt. Gleichzeitig wurden sie von der folgenden Logik geleitet: Wenn im Merkmalsraum alle Elemente derselben Klasse kompakt in der Nähe eines Punkts gruppiert sind, ist es weniger wahrscheinlich, dass sich Vorzeichen für negative Beispiele in der Nähe desselben Punkts befinden. Daher haben wir als Hauptkriterium für die Filterung den euklidischen Abstand zum statistischen Zentrum einer bestimmten Klasse verwendet.

Um die Hypothese zu testen, führten wir das folgende Experiment durch: Wir trainierten Modelle zum Erkennen einer kleinen Teilmenge japanischer Zeichen aus Silbenalphabeten (dem sogenannten Kana). Zusätzlich zur Trainingsstichprobe haben wir 3 künstliche Grundlagen negativer Beispiele untersucht:

• Paare - eine Reihe von Paaren europäischer Zeichen
• Schnitte - Fragmente japanischer Linien, die in Lücken geschnitten sind, keine Zeichen
• Nicht Kana - andere Zeichen aus dem japanischen Alphabet, die nicht mit der betrachteten Teilmenge zusammenhängen

Wir wollten den klassischen Ansatz mit der Cross-Entropy-Loss-Funktion und den Ansatz mit Center Loss in ihrer Fähigkeit vergleichen, negative Beispiele zu filtern. Die Filterkriterien für negative Beispiele waren unterschiedlich. Im Fall von Cross Entropy Loss haben wir die Netzwerkantwort der letzten Schicht verwendet, und im Fall von Center Loss haben wir den euklidischen Abstand zum statistischen Zentrum der Klasse im Attributraum verwendet. In beiden Fällen haben wir den Schwellenwert der entsprechenden Statistik gewählt, bei dem nicht mehr als 3% der positiven Beispiele aus der Testprobe eliminiert werden, und den Anteil negativer Beispiele aus jeder Datenbank untersucht, der bei diesem Schwellenwert eliminiert wird.


Wie Sie sehen können, filtert der Center Loss-Ansatz negative Beispiele besser heraus. Darüber hinaus hatten wir in beiden Fällen keine Bilder von negativen Beispielen im Lernprozess. Dies ist tatsächlich sehr gut, da es im allgemeinen Fall keine leichte Aufgabe ist, eine repräsentative Basis aller negativen Beispiele im OCR-Problem zu erhalten.

Wir haben diesen Ansatz auf das Problem der Erkennung japanischer Zeichen (auf der zweiten Ebene eines zweistufigen Modells) angewendet, und das Ergebnis hat uns gefallen: Die Anzahl der linearen Teilungsfehler wurde erheblich reduziert. Obwohl die Fehler bestehen blieben, konnten sie bereits nach bestimmten Typen klassifiziert werden: seien es Zahlenpaare oder Hieroglyphen mit einem festsitzenden Interpunktionssymbol. Für diese Fehler war es bereits möglich, eine synthetische Basis negativer Beispiele zu bilden und diese im Lernprozess zu verwenden. Wie dies getan werden kann, wird weiter diskutiert.

Verwendung der Basis negativer Beispiele im Training

Wenn Sie eine Sammlung negativer Beispiele haben, ist es dumm, sie nicht im Lernprozess zu verwenden. Aber lassen Sie uns darüber nachdenken, wie dies getan werden kann.

Betrachten Sie zunächst das einfachste Schema: Wir gruppieren alle negativen Beispiele in einer separaten Klasse und fügen der Ausgabeschicht, die dieser Klasse entspricht, ein weiteres Neuron hinzu. Jetzt haben wir am Ausgang eine Wahrscheinlichkeitsverteilung für die Klasse N + 1 . Und wir lehren dies den üblichen Cross-Entropy-Verlust.

Das Kriterium, dass das Beispiel negativ ist, kann als Wert der entsprechenden neuen Netzwerkantwort betrachtet werden. Aber manchmal können echte Charaktere von nicht sehr hoher Qualität als negative Beispiele eingestuft werden. Ist es möglich, den Übergang zwischen positiven und negativen Beispielen reibungsloser zu gestalten?

Tatsächlich können Sie versuchen, die Gesamtzahl der Ausgaben nicht zu erhöhen, sondern das Modell beim Lernen einfach dazu bringen, niedrige Antworten für alle Klassen zurückzugeben, wenn Sie negative Beispiele auf die Eingabe anwenden. Dazu können wir dem Modell nicht explizit die Ausgabe N + 1 hinzufügen, sondern einfach den Wert –max aus den Antworten für alle anderen Klassen zum Element N + 1 hinzufügen. Wenn dann negative Beispiele auf die Eingabe angewendet werden, versucht das Netzwerk, so viel wie möglich zu tun, was bedeutet, dass die maximale Antwort versucht, so wenig wie möglich zu machen.



Genau ein solches Schema haben wir auf der ersten Ebene eines Zwei-Ebenen-Modells für Japaner in Kombination mit dem Center-Loss-Ansatz auf der zweiten Ebene angewendet. So wurden einige der negativen Beispiele auf der ersten Ebene und einige auf der zweiten Ebene gefiltert. In Kombination ist es uns bereits gelungen, eine Lösung zu erhalten, die in den allgemeinen Erkennungsalgorithmus eingebettet werden kann.

Im Allgemeinen kann man sich auch fragen: Wie kann man die Basis negativer Beispiele im Ansatz mit Center Loss verwenden? Es stellt sich heraus, dass wir die negativen Beispiele, die sich in der Nähe der statistischen Zentren der Klassen im Attributraum befinden, irgendwie verschieben müssen. Wie kann man diese Logik in die Verlustfunktion einbauen?

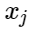
Lass - Anzeichen negativer Beispiele und - Klassenzentren. Dann können wir den folgenden Zusatz für die Verlustfunktion in Betracht ziehen:



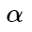
Hier - eine gewisse zulässige Lücke zwischen dem Zentrum und den negativen Beispielen, innerhalb derer negative Beispiele bestraft werden.

Die Kombination von Center Loss mit dem oben beschriebenen Additiv haben wir beispielsweise für einige einzelne Klassifikatoren erfolgreich angewendet, um koreanische Zeichen zu erkennen.

Schlussfolgerungen

Im Allgemeinen können alle oben beschriebenen Ansätze zum Filtern der sogenannten „negativen Beispiele“ bei allen Klassifizierungsproblemen angewendet werden, wenn Sie eine implizit stark unausgeglichene Klasse im Vergleich zu den anderen haben, ohne eine gute Basis von Vertretern, mit der jedoch irgendwie gerechnet werden muss . OCR ist nur eine bestimmte Aufgabe, bei der dieses Problem am akutesten ist.

All diese Probleme treten natürlich nur auf, wenn neuronale Netze als Hauptmodell für die Erkennung einzelner Zeichen verwendet werden. Bei Verwendung der End-to-End-Zeilenerkennung als separates Modell tritt ein solches Problem nicht auf.

OCR New Technologies Group