Das von Dutzenden von Sensoren eingefügte „Forschungsobjekt“ bei dynamischen Tests in vollem Umfang (z. B. bei der Untersuchung der Schwingungsaktivität des Fahrzeugs) liefert uns leicht eine große Datenmenge, aber es ist oft nicht klar, was damit zu tun ist. Gleiches gilt für die Simulationsmodellierung dynamischer Prozesse von Systemen mit einer Vielzahl von Freiheitsgraden.
Dies mag für diejenigen, die nicht regelmäßig auf ein Problem stoßen, nicht ganz klar sein, aber es ist in der Regel fast sinnlos, die entsprechende Animation eines zeitlich und räumlich stochastischen Prozesses zu betrachten. Wo es bricht oder warum es so zittert - normalerweise „nicht sichtbar“. Was sie neben der Animation erfunden haben, werde ich Ihnen weiter unten sagen, aber ich werde dies empfehlen.
Durch ein elementares Verfahren kann man auch die räumlichen "Formen" der Schwingungen selbst erhalten, außerdem sind es genau die tatsächlichen Manifestationen unter gegebenen Belastungsbedingungen und die Intensität ihrer Manifestation (Dispersion; falls gewünscht die Prozesse selbst).
Quelle
Mehrkanal
der Prozess
 | Zersetzung
|
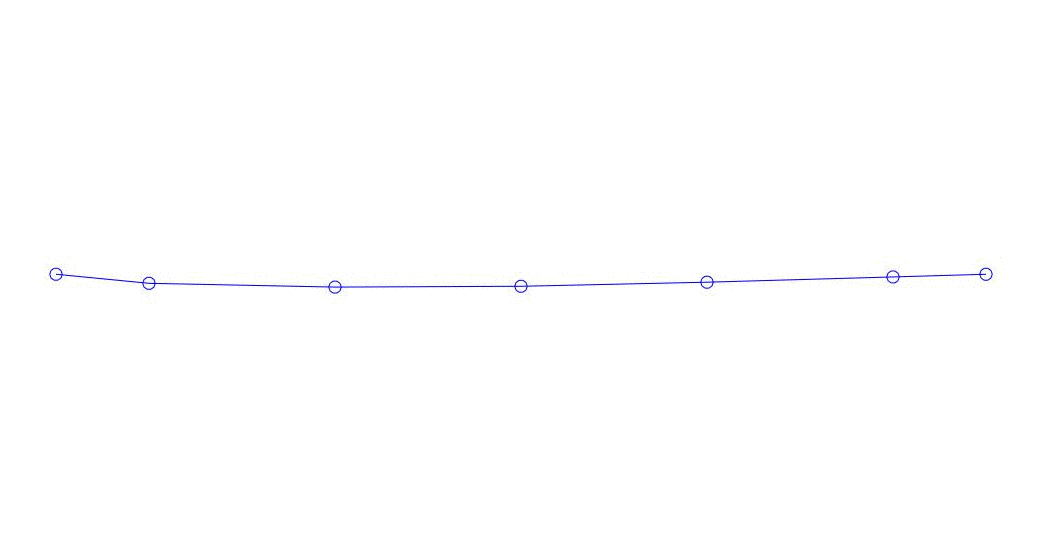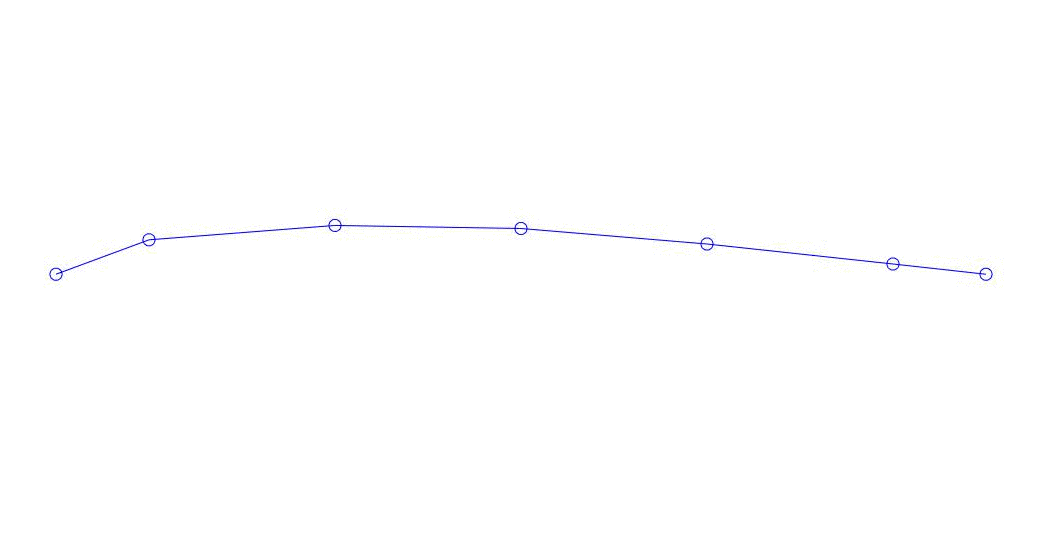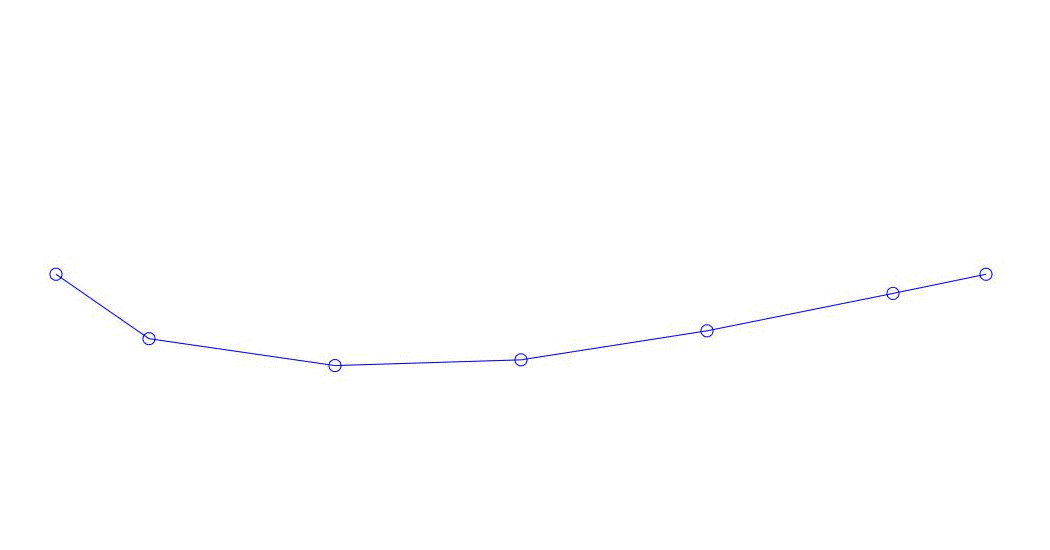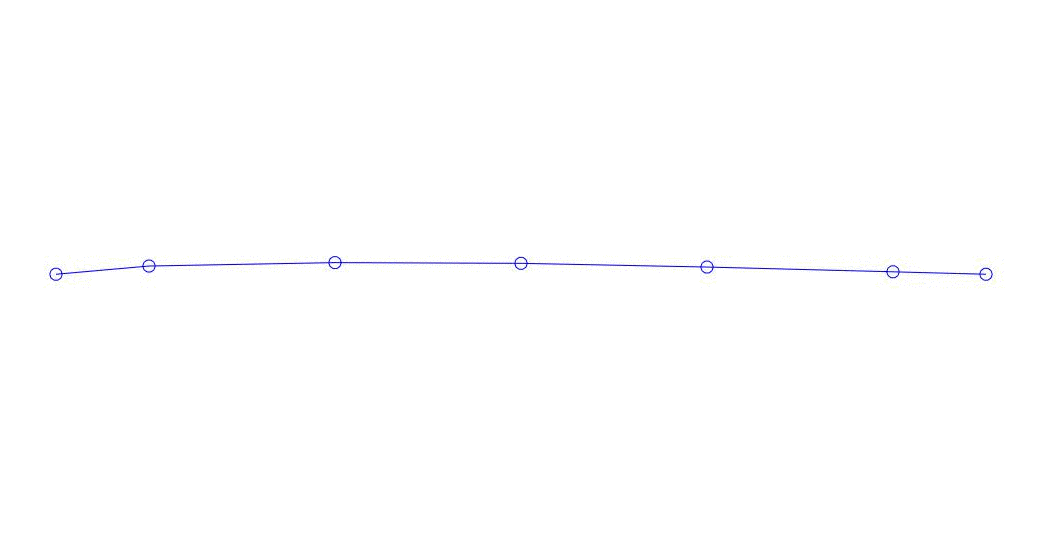
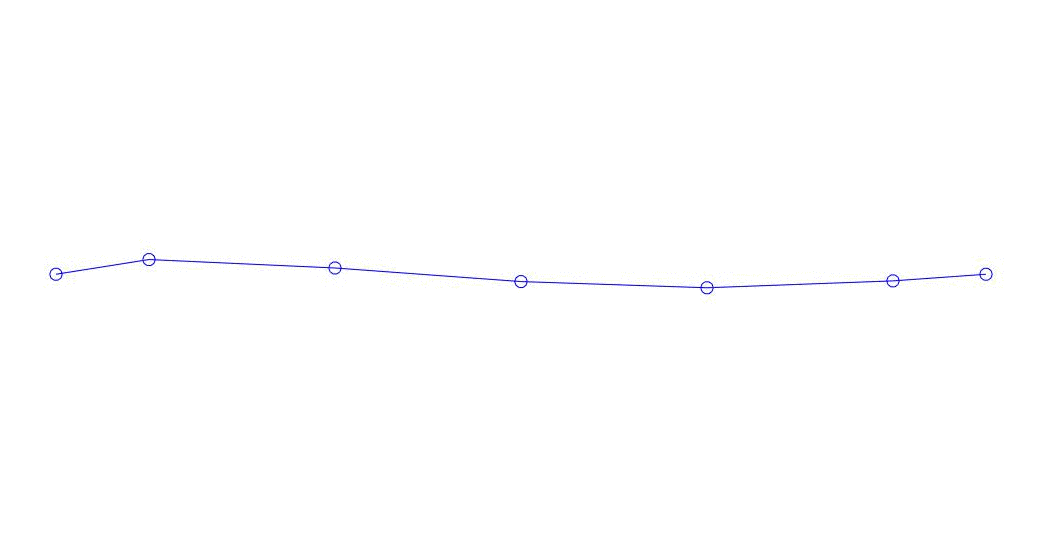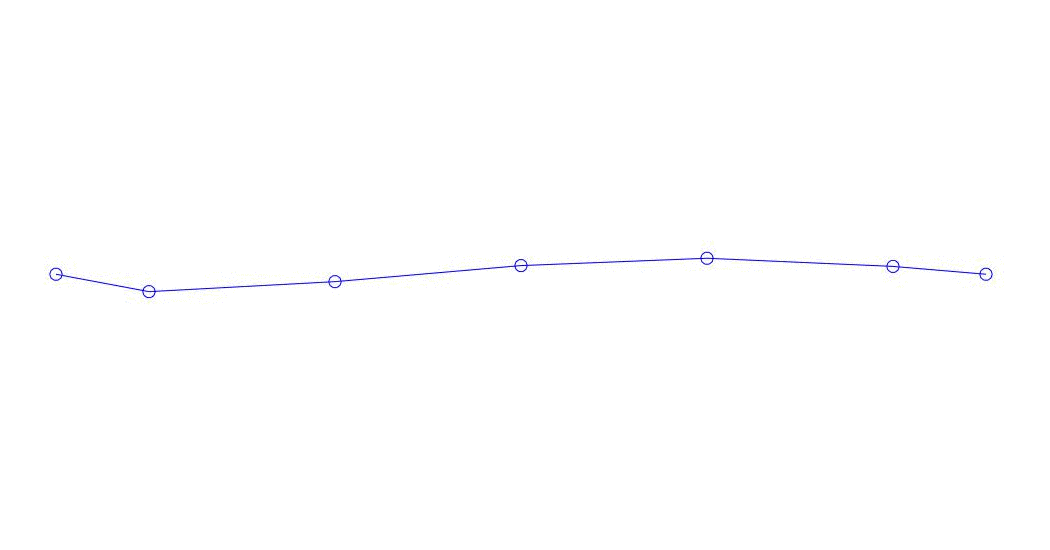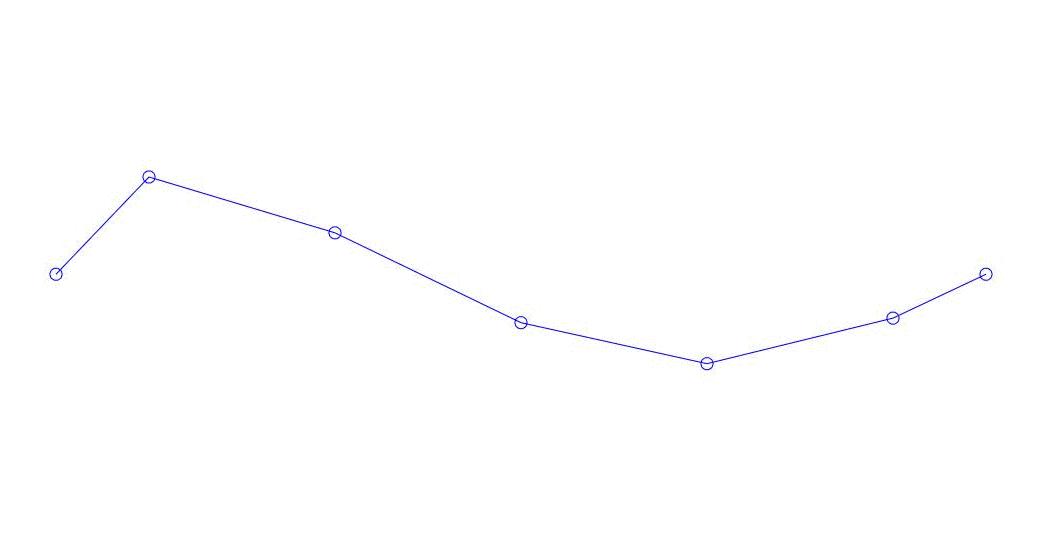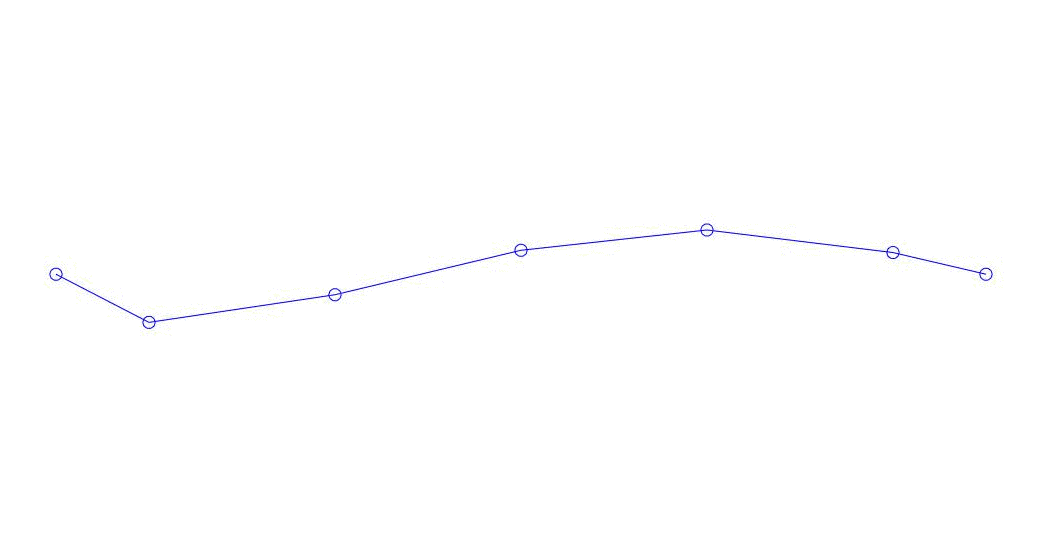
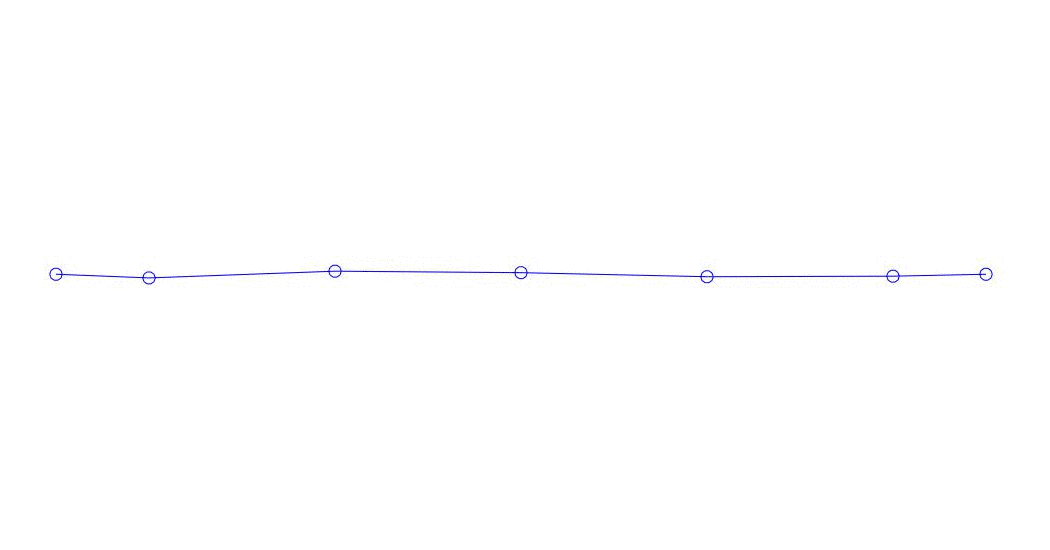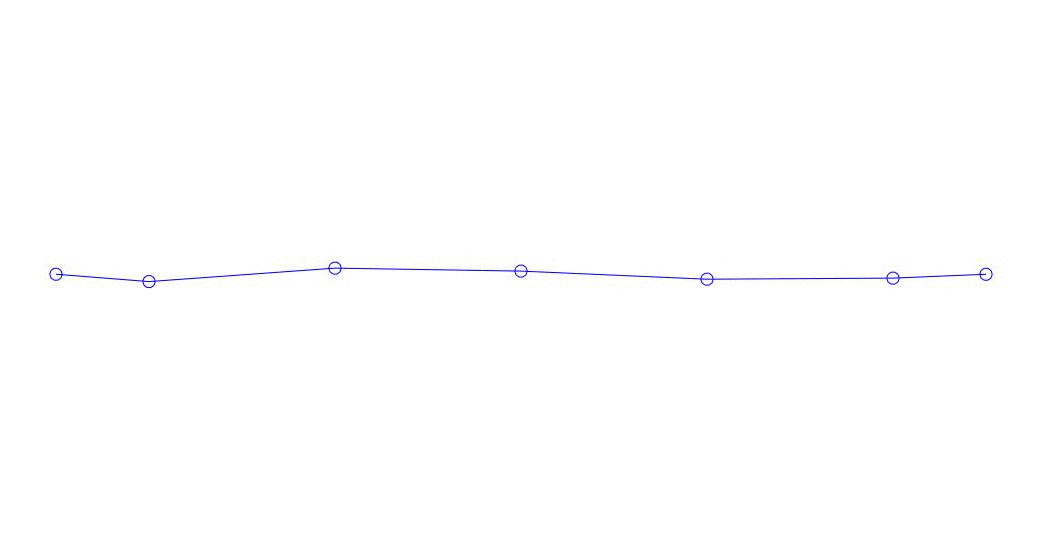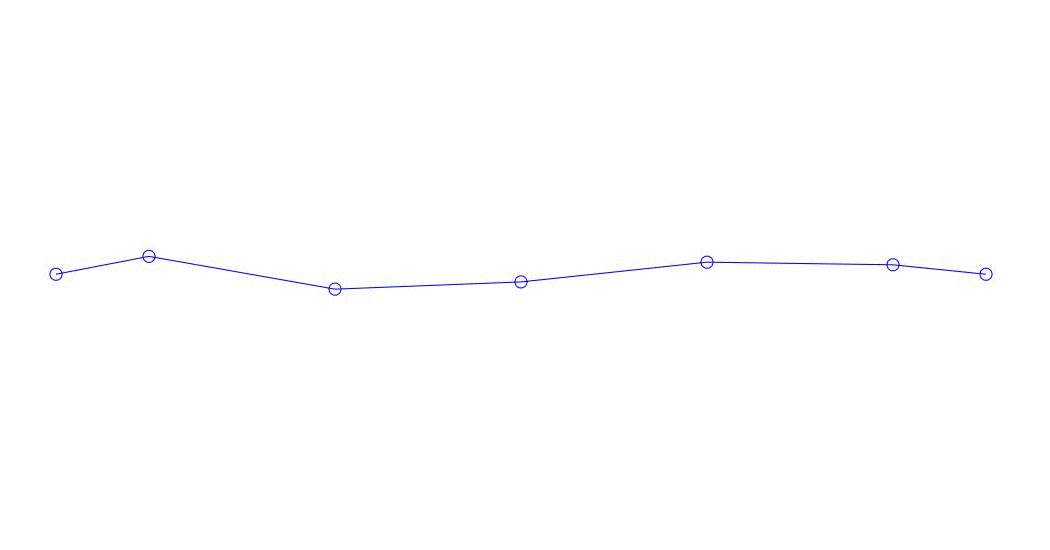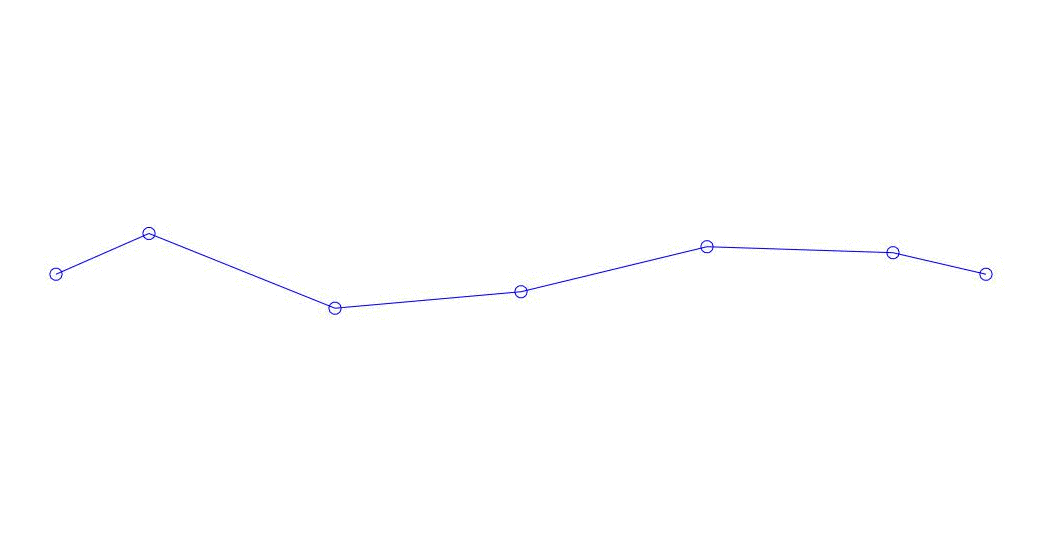
Fig. 1 Zerlegung einer Mehrkanalantwort in Pseudoform. „Schnur in einem viskosen Medium“ (siehe Abbildung 2)
Neben der Animation sind "paarweise" Studien (gegenseitige Spektren usw.) bekannt, die natürlich kein allgemeines Bild liefern.
Solche Verfahren sind ziemlich offensichtlich - durch "Ausschneiden" sehr schmaler Bänder des Spektrums, die den Resonanzpeaks in den Spektrogrammen entsprechen, erzeugen Spektrogrammverfahren (wiederum "paarweise") fast Formen von nahezu harmonischen (stark korrelierten) Schwingungen.
Neben der offensichtlichen technischen Komplexität besteht der Nachteil solcher Methoden darin, dass Sie normalerweise einen Referenzkanal "erfolgreich" auswählen müssen, was nicht immer möglich ist. Infolgedessen treten in den gegenseitigen Phasen der Prozesse sehr große Fehler auf. Darüber hinaus kann sich die ausgeprägte räumliche Form von Schwingungen ohne solche Fehler aufgrund der Eigenschaften eines linearen Systems als „komplex“ (nichtphasig) herausstellen, dessen Wert für die nachfolgende subjektive Analyse normalerweise (nicht immer) erheblich abnimmt.
Es ist eine 4-Kanal-Studie über Torsionsschwingungen (das Trägersystem eines durchschnittlichen Busses) bekannt, die in einem Prozess anhand der räumlichen Schwingungsform zugeordnet wird, die durch die Inspiration des Forschers bestimmt wurde. Die Messwerte von zwei Sensoren, die sich diagonal an den Ecken des Körpers befinden, wurden hinzugefügt (entnommen aus „+“) Sie wurden vom Zeugnis zweier anderer achsensymmetrisch angeordneter Zeugen abgezogen (von „-“ übernommen).
Selbst mit einer kleinen Anzahl von Sensoren ist dieser Ansatz möglicherweise nicht ganz gut. Zum Beispiel ist der Rahmen eines Lastwagens im Submotor- (Front-) Teil bzw. in einer Torsionsform in der Regel viel formbarer, möglicherweise sollte er in einer komplexeren Form angenommen werden (wahrscheinlich mit einigen „ansteigenden“ Koeffizienten für die Frontsensoren - und gleichzeitig die Frage, ob das Akzeptierte begründet wird Modelle). Bei einer größeren Anzahl von Überwachungskanälen ist dies alles sehr kompliziert und schlecht gerechtfertigt.
Die explizite Trennung (in getrennte Prozesse) mehrerer Schwingungsmodi (Modi), die zuvor aus einem anderen Experiment oder einer anderen Simulation bestimmt wurden, wurde einmal von mir (wahrscheinlich nicht nur von mir) vorgeschlagen und von meinem Chef damals als "Methode der modalen Zersetzung" bezeichnet. Es sollte die Ergebnisse von Feldtests so analysieren und die Vektoren ihrer eigenen Form durch Bench-Tests (oder Finite-Elemente-Modellierung) bestimmen.
Eigentlich haben sie das getan, aber gleichzeitig hat sich herausgestellt, dass.
Es ist klar, dass „Bench-Experimentatoren“ im Gegensatz zu „Polygon-Experimentatoren“ für die synchrone Beobachtung einen wirklich störenden Prozess zur Verfügung haben. Dies gab ihnen einen großen Vorteil: Sie konnten die tatsächlichen Übertragungsfunktionen bestimmen und mithilfe der verfügbaren Hardware und Software experimentell ihre eigenen Formen und Frequenzen von Strukturschwingungen bestimmen (basierend auf Kopplung, „Schneiden“ der Frequenzbereiche „per Auge“ und Anzeigen an das System, wie viele Formen es gibt finden; auch eher Kunst als Wissenschaft, aber immer noch).
Allerdings. Sie vermieden es eindeutig, ein Objekt wie eine Fahrzeugbaugruppe zu erkunden, und bevorzugten einzelne Rahmen, Stützkörper usw. - Gegenstände mit sehr geringer Dämpfung. Es geht um modale Bench-Tests - die Bestimmung von Eigenfrequenzen und -formen. Nicht über Simulation. Plausible intrinsische Schwingungsmoden an etwas stärker gedämpften Objekten können im Prinzip experimentell erhalten werden, sind jedoch wesentlich komplizierter.
Es stellte sich heraus, dass es sich bei sehr wertvollen Informationen um diese "Vorlieben" handelte. Wenn auch nur sehr kurz, dann sind es trotz der "Schönheit" der Idee kaum wert, nur die Schlussfolgerungen zu ziehen, die später nach und nach gezogen wurden: Es ist kaum wert, die Antwort genau auf die wirklich richtigen Formen der Konstruktion zu zerlegen.
Wenn es "an Ihren Fingern" ist, ist der Grund wahrscheinlich mit einer hohen Wahrscheinlichkeit, z. B. - abhängig von der äußeren Störung werden "natürliche Schwingungsmodi" (genauer gesagt stationäre "modale" Prozesse, die natürlichen Schwingungsmodi entsprechen) höchstwahrscheinlich so sein oder sie sind ansonsten miteinander korreliert und bilden tatsächlich einige andere räumliche Formen von Schwingungen, die sich in dem einen oder anderen Grad von ihren eigenen unterscheiden, und dies äußert sich natürlich in einer starken Abhängigkeit von der Dämpfung der Struktur.
Als kurze Erklärung "aus dem Gegenteil" - zwei verschiedene "ungedämpfte" Harmonische sind natürlich immer nichts miteinander korreliert. (Erklärung. Der oben erwähnte Effekt des "Mischens eigener Formen" wird sowohl in Abwesenheit von "signifikanten Nichtlinearitäten" als auch außerhalb von "komplexen Formen" mit "unverhältnismäßiger" Dämpfung in linearen Systemen beobachtet.)
Auf der Grundlage des Vorstehenden wird vorgeschlagen, die Reaktion des Systems als die Summe mehrerer korrelationsunabhängiger Prozesse wie bestimmter Schwingungsformen (Biegung, Torsion usw.) darzustellen. Eine solche Analyse ist sehr einfach und liefert in der Regel sehr wertvolle Ergebnisse. Die erhaltenen Formen können den Eigenschwingungsmodi des Systems ähnlich sein oder auch nicht, aber sie spiegeln immer das Verhalten des Systems genau unter Bedingungen realen äußeren Einflusses wider. Darüber hinaus reflektieren sie so einfach und informativ wie möglich, und ihre Reihenfolge, geordnet nach ihren Varianzen, ist eine ungefähre Reihe.
Um die für uns interessante Zerlegung zu erhalten, betrachten wir (1),
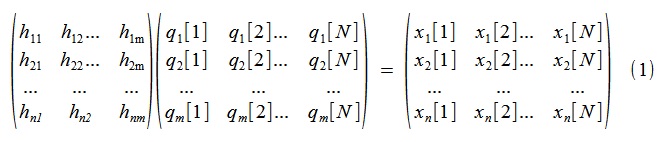
oder gleich kompakt (2),
Dabei ist
x die n-Kanal-physikalische Antwort des Systems mit der Dauer von N Proben, die direkt im Experiment erhalten wurden,
q der echte "modale" m-Kanal-Prozess mit nicht miteinander korrelierten Kanälen, H die Spaltenmatrix, die die gewünschten gleichphasigen ("realen") Schwingungsmodi beschreibt.
Im Allgemeinen wird anschließend m <n erwartet (die Anzahl der Formen ist geringer als die Anzahl der physikalischen Antwortkanäle), aber zunächst nehmen wir an, dass m = n ist, und wenn H und
q den Rang n haben, (2) in jedem Fall ohne Residuum erfüllt ist, kommen wir offensichtlich zu
| H · Rqq [0] · H T = Rxx [0] (3) |
oder genauer
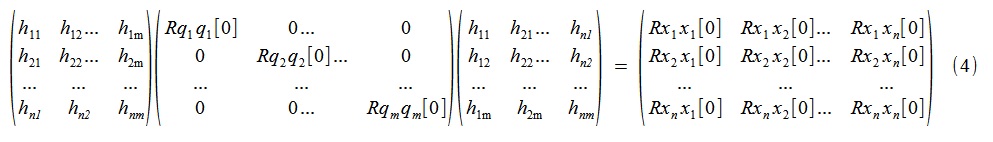
Das heißt, die Suche nach den gesuchten solchen "pseudo-richtigen" Schwingungsmoden und den entsprechenden unkorrelierten (mit null Verzögerung) Prozessen
q reduziert sich auf die spektrale Zerlegung (in Bezug auf Eigenvektoren und Zahlen) der symmetrischen Matrix Rxx [0] (zusammengesetzt aus den Werten der Auto- und Kreuzkorrelationen der Prozesse
x für lag Δτ = 0) Seine eigenen orthonormalen Vektoren geben uns die gewünschten Formen, und die realen Eigenwerte geben die Varianzen der entsprechenden Prozesse an (zusätzlich zu den signifikanten gibt es höchstwahrscheinlich Varianzen von ~ 0, also in der Praxis normalerweise m <n). Falls gewünscht, können Sie die Prozesse weiterhin selbst in Form von temporären Realisierungen erstellen, ihre Spektren finden usw.
Um dies zu verdeutlichen, betrachten wir ein Modell eines linearen mechanischen Systems mit fünf Freiheitsgraden, das ungefähr das Verhalten einer Saite in einem viskosen Medium simuliert (Abb. 2).
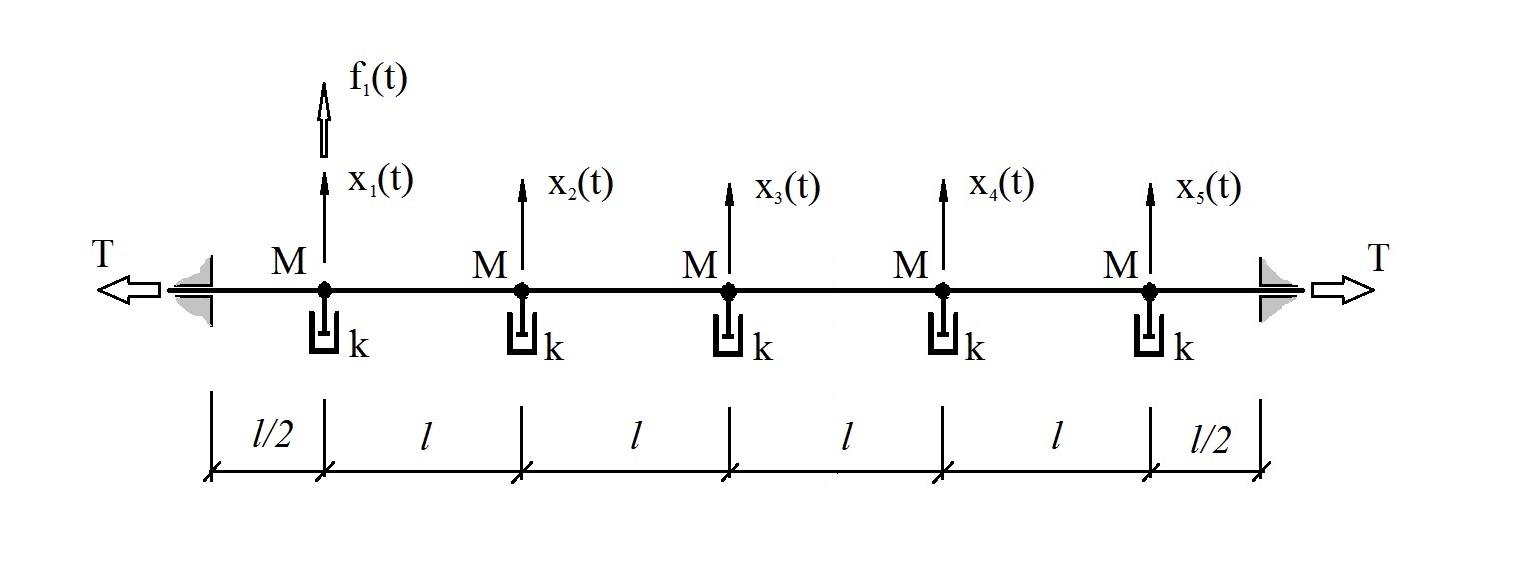Abb. 2 Testsystem.oszillierend unter dem Einfluss einer stochastischen Störung f
1 [i] vom Typ des rosa Rauschens (Fig. 3), Abtastintervall & Dgr; t = 0,01 s, Implementierungslänge 25000 Abtastungen (im Folgenden werden die PSD-Schätzungen durch das Welch-Verfahren erhalten, Segmentlänge 1024, das Hamming-Fenster wird angewendet und 60% Überlappung der Segmente.)
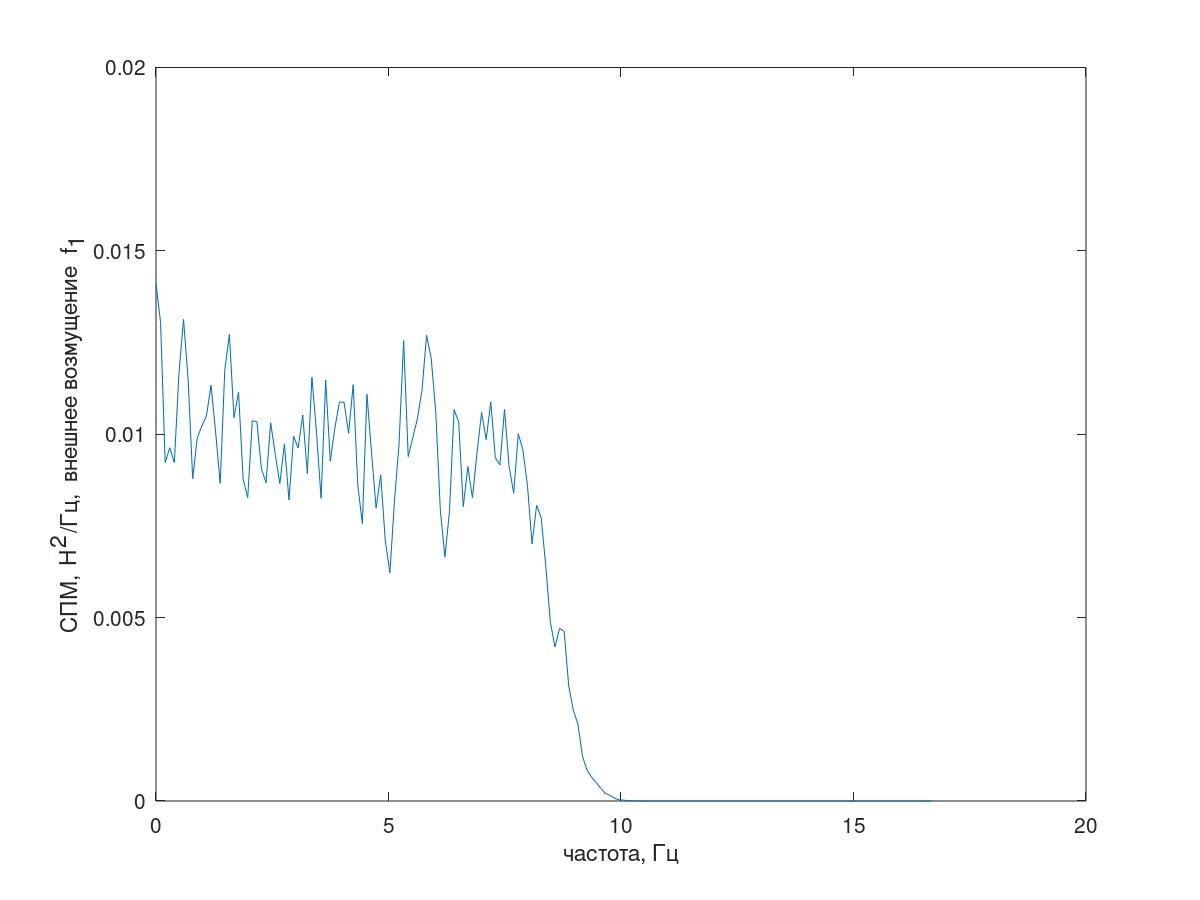Abb. 3 Spektrum der äußeren Störung.
Ein Fragment der vorübergehenden Implementierung der Störung ist in Fig. 4 gezeigt.
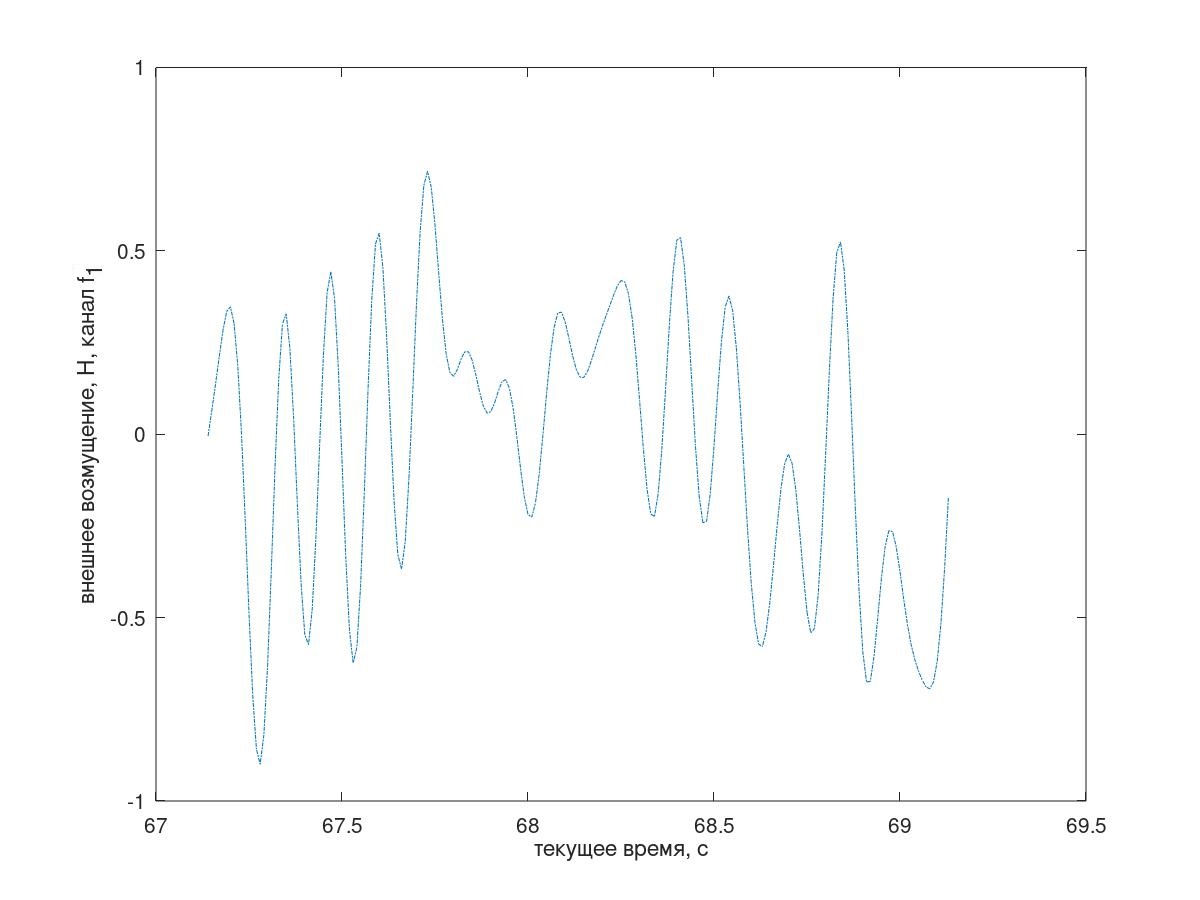
Abb. 4 Ein Fragment der temporären Implementierung der eingehenden Störung
In kontinuierlicher Zeit ist das Modell ein System von Diffusionsgleichungen (6),
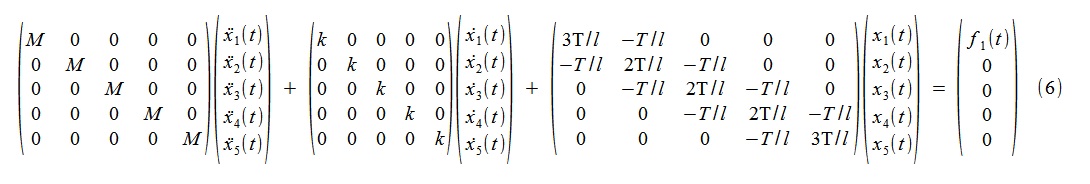
wobei M = 1 kg, k = 10 kg / s, T = 2000 N, 1 = 1 m.
Die entsprechenden (es ist klar, welche) Matrizen sind numerisch gleich den folgenden:
Einer der Frequenzgänge des Systems ist in Fig. 5 gezeigt.
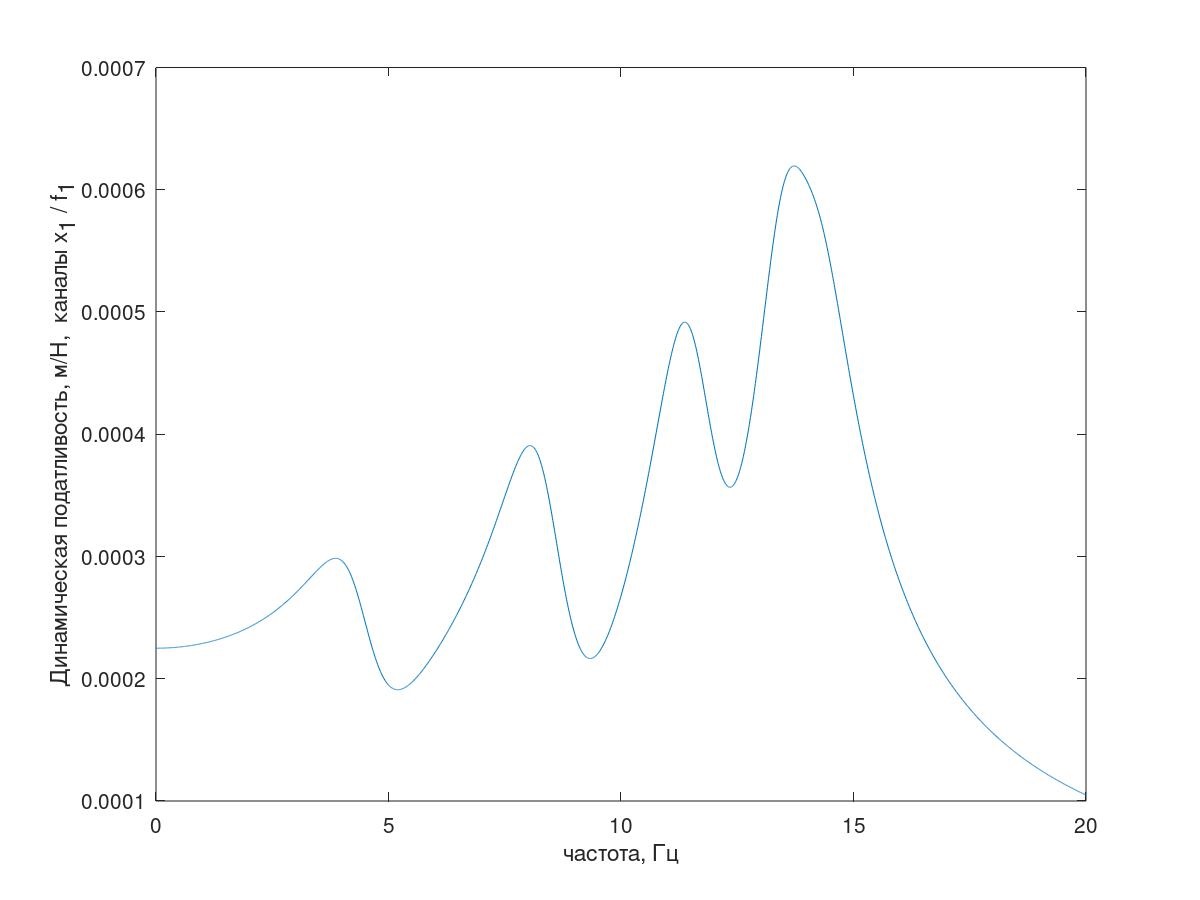Abb. 5. Frequenzgang des Testsystems(Erklärung - mit der Anzahl der Resonanzspitzen ist alles in Ordnung, eine Erklärung dieses Frequenzgangs des Systems mit bedingt reduzierter Dämpfung (k = 1 kg / s) ist in Abb. 5 dargestellt.)
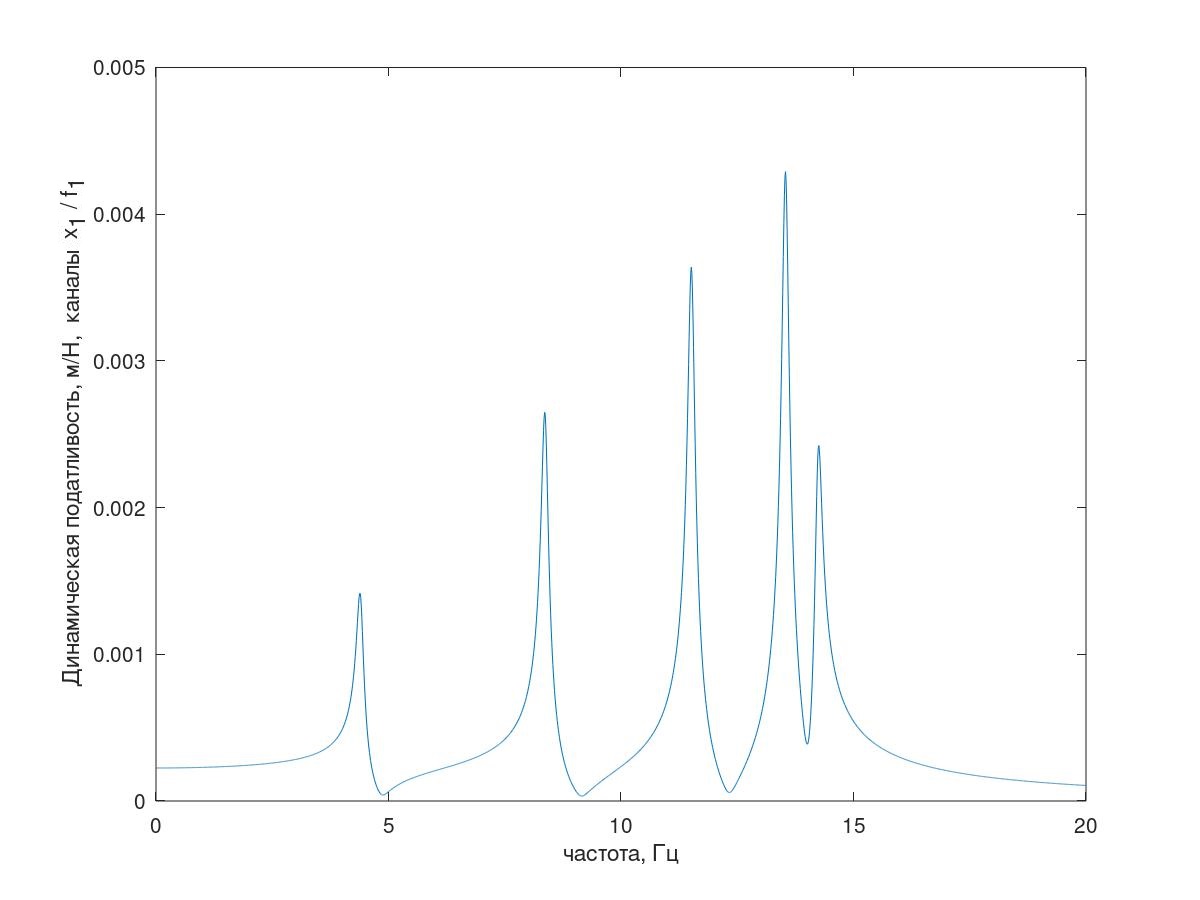Abb. 6 Erklärung für fünf Resonanzen.
Für die Simulation in diskreter Zeit wird ein Finite-Differenzen-Modell verwendet (Raman-Modelle funktionieren gut in kleinen Abtastintervallen, wie
gezeigt wurde ).
Ein kleiner Exkurs. Einige Zeit später wurde im Rahmen einer anderen Arbeit eine Finite-Differenzen-Modellierung dieses Testsystems mit anderen Mitteln durchgeführt (Xcos \ Simulink). Mathematisch sind die Modelle identisch. Es wurden animierte Bilder der Reaktion des Systems auf einen einzelnen Impuls am Knoten Nr. 1 und am Knoten Nr. 3 erhalten. Die Ergebnisse sind hier unter dem Gesichtspunkt der Verifikation des Finite-Differenzen-Modells interessant.
(Die "unvorhersehbare" Pufferung von freien Software-Frames verdirbt die Bilder etwas, insbesondere die zweite, aber im Prinzip ist das Ergebnis sehr gut.)
Aber zurück zu unserem Matlab (GNUOctave) Modell. Das resultierende Antwortspektrum ist in Fig. 7 gezeigt.
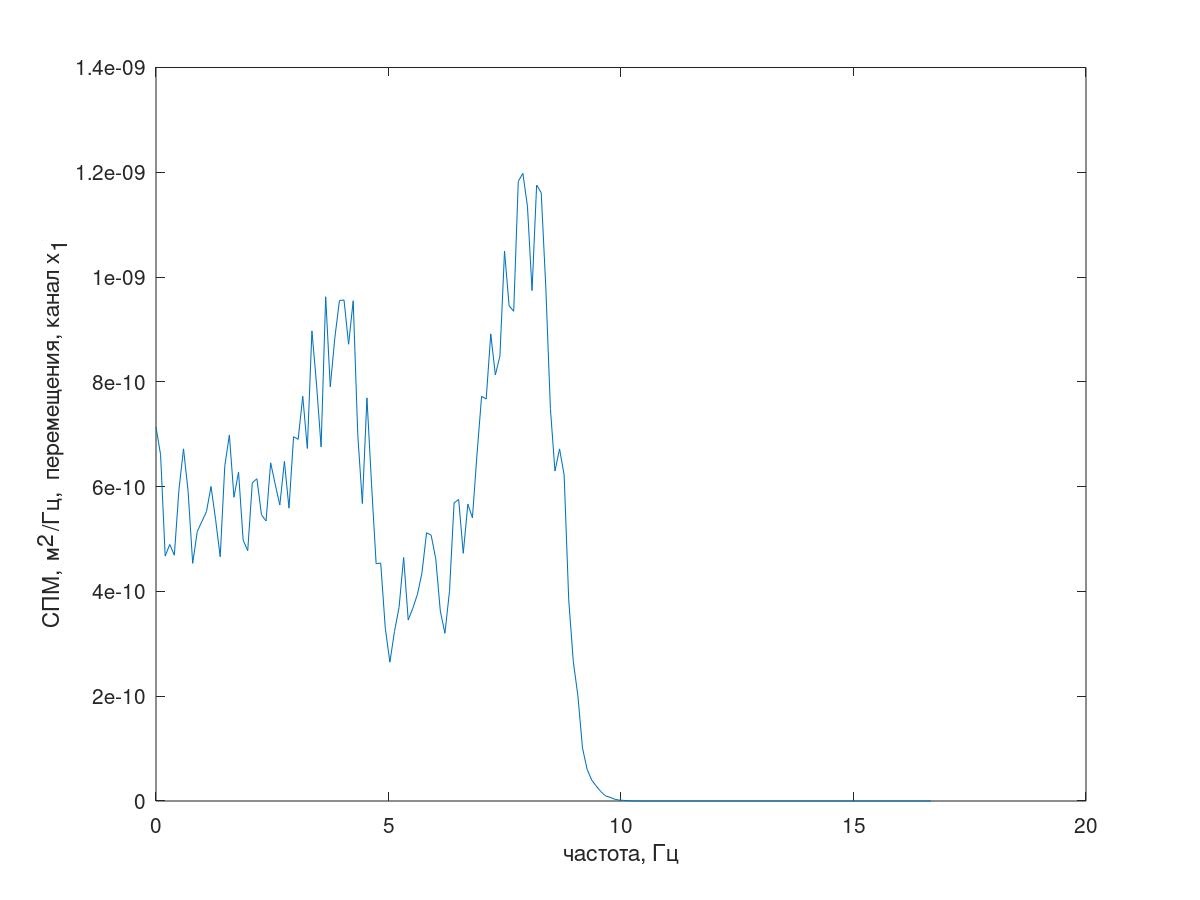Abb. 7 Antwortspektrum (Kanal x 1 )Ferner wurde das Korrelationsverfahren verwendet, um die Werte von Auto- und Kreuzkorrelationen der Antwortkanäle zu finden.
Die Ergebnisse der Anwendung der diskutierten Methode: Varianzen von pseudomodalen Prozessen Rqq und pseudo-unterschiedlichen Formen von H selbst wurden gefunden:
Die ersten drei Prozesse in der Zerlegung, die Animation des gesamten Mehrkanalprozesses und die entsprechenden ersten drei Schwingungsmodi in 32 Proben (von 6714 bis 6746 Proben, d. H. Von 67,13 s in Bezug auf die Menge) sind offensichtlich quantitativ signifikant (durch die Werte ihrer Dispersionen in Rqq). Die aktuelle Zeit von 67,63 s) ist in Abb. 1 am Anfang des Artikels dargestellt. Wie Sie sehen können, haben diese Pseudoform einige Ähnlichkeiten mit ihren eigenen Formen von Saitenschwingungen.
Die gesammelte Erfahrung zeigt die folgenden Merkmale dieser Methode.
- Das Verfahren ist empfindlich gegenüber Fremdgeräuschen, einschließlich hohe Frequenz. Es besteht die Gefahr, dass „zufällige“ Ergebnisse (mit einem großen zufälligen Fehler) und die offensichtliche Irreproduzierbarkeit der experimentellen Ergebnisse erzielt werden. Es ist notwendig, den nicht arbeitenden (quantitativ unbedeutenden) Teil des Frequenzbereichs des Mehrkanalsignals sorgfältig herauszufiltern. (Zu einer Zeit wurde die Arbeit in dieser Richtung sogar aufgrund von Berichten von Experimentatoren über das "Fehlen" der Korrelation zwischen Kanälen - die Wirkung von starkem Rauschen - eingestellt.)
- Die besten Ergebnisse wurden mit der Anzahl von Beobachtungskanälen erhalten, die signifikant größer als die Anzahl der erwarteten Manifestation von Schwingungsformen (die Anzahl von Resonanzpeaks im untersuchten Bereich) waren, d.h. für m << n.
- Mit hohen Q-Faktoren scheinen Pseudoformsysteme zu den wahren intrinsischen Modi des Systems zu tendieren. Die mit solchen Systemen erzielten Ergebnisse sind im Falle von Rauschen stabiler.
- Wenn das Paar von Eigenwerten Rxx [0] zusammenfällt oder sogar konvergiert, wird das Paar entsprechender Pseudoformen anscheinend bis zu ihren unabhängigen linearen Kombinationen bestimmt - solche Formen können unter gegebenen experimentellen Bedingungen nicht untereinander getrennt werden.
- Offensichtlich ist es beim Vergleich der wahren Formen (gefunden durch andere Methoden) und der betrachteten Pseudoformen mit einiger Wahrscheinlichkeit möglich, die Anwendungspunkte der externen Störung (insbesondere bei einer Störung mit kleinen Kanälen) zu finden, wenn ein solches Problem relevant ist.