Einführung
Das englische Wort Wavelet (vom französischen "Ondelette") bedeutet wörtlich "kurze (kleine) Welle". In verschiedenen Übersetzungen ausländischer Artikel ins Russische gibt es auch Begriffe: "Burst", "Burst-Funktion", "Low-Wave-Funktion", "Wave" usw.
Die Wavelet-Transformation (VP) wird häufig für die Signalanalyse verwendet. Darüber hinaus findet es große Anwendung im Bereich der Datenkomprimierung. Der VP eines eindimensionalen Signals ist seine Darstellung in Form einer verallgemeinerten Reihe oder eines Fourier-Integrals über ein System von Basisfunktionen.
psiab(t)= frac1 sqrta psi left( fract−ba right) , (1)
konstruiert aus dem Mutter (Quelle) Wavelet
psi(t) Besitz bestimmter Eigenschaften aufgrund von Zeitverschiebungsoperationen (b) und zeitlichen Skalenänderungen (a).
Multiplikator
1/ sqrta gewährleistet die Unabhängigkeit der Funktionsnorm (1) von der Skalierungszahl (a). Für die angegebenen Werte der Parameter a und b gilt die Funktion
psiab(t) und es gibt ein Wavelet, das vom Mutter-Wavelet erzeugt wird
psi(t) .
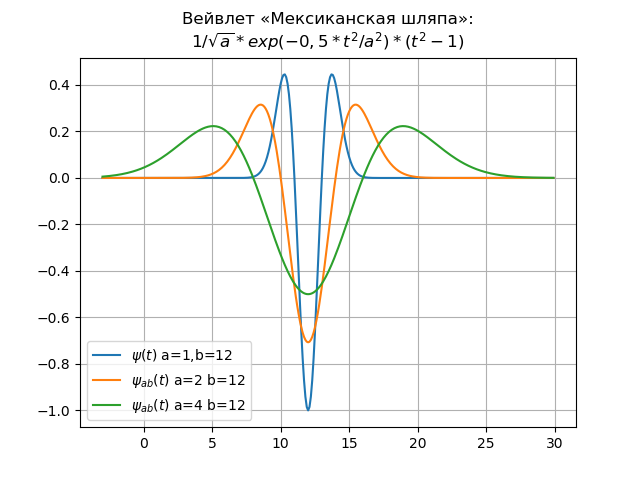
Ein Beispiel ist das mexikanische Hut-Wavelet im Zeit- und Frequenzbereich:
Wavelet-Liste für Zeitbereichfrom numpy import* import matplotlib.pyplot as plt x= arange(-4,30,0.01) def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f plt.title(" « »:\n$1/\sqrt{a}*exp(-0,5*t^{2}/a^{2})*(t^{2}-1)$") y=[w(1,12,t) for t in x] plt.plot(x,y,label="$\psi(t)$ a=1,b=12") y=[w(2,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=2 b=12") y=[w(4,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=4 b=12") plt.legend(loc='best') plt.grid(True) plt.show()
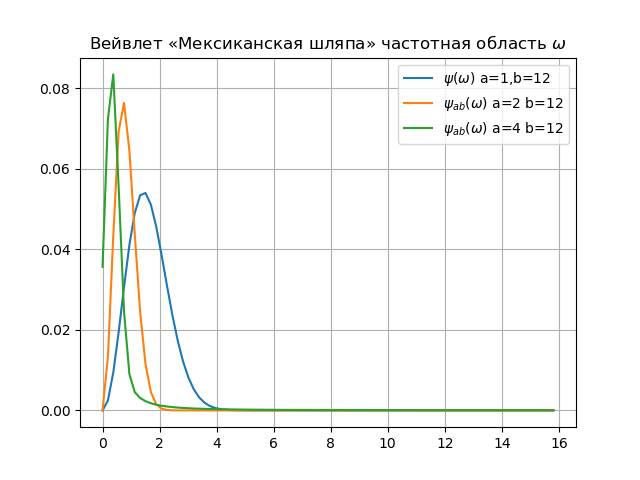
Auflistung für das Wavelet-Spektrum from numpy import* from pylab import * from scipy import * import os def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f x= arange(-4,30,0.2) def plotSpectrum(y,Fs): n = len(y) k = arange(n) T = n/Fs frq = k/T frq = frq[range(int(n/2))] Y = fft(y)/n Y = Y[range(int(n/2))] return Y,frq xlabel('f (Hz)') ylabel('|Y(f)|') Fs=1024.0 y=[w(1,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi(\omega)$ a=1,b=12") y=[w(2,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=2 b=12") y=[w(4,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=4 b=12") plt.title(" « » $\omega$") legend(loc='best') grid(True) show()
 Fazit:
Fazit:1. Zwischen dem Konzept der Fourier-Harmonischen und der Skala des Wavelets besteht tatsächlich eine Beziehung. Die Hauptsache in dieser Beziehung ist das umgekehrte Verhältnis der Eigenfrequenz und der Skala. Durch Verringern der Skalierung erhöhen wir außerdem die Bandbreite des Wavelet-Spektrums.
2. Durch Ändern der Skala (Erhöhen von a führt zu einer Verengung des Fourier-Spektrums der Funktion
psiab(t) ) können Wavelets den Unterschied in den Eigenschaften auf verschiedenen Skalen (Frequenzen) erfassen und aufgrund der Verschiebung die Signaleigenschaften an verschiedenen Punkten des gesamten untersuchten Intervalls analysieren. Daher erhalten sie bei der Analyse instationärer Signale aufgrund der Lokalität der Wavelets einen signifikanten Vorteil gegenüber der Fourier-Transformation, die nur globale Informationen über die Frequenzen (Skalen) des analysierten Signals liefert, da das verwendete Funktionssystem (der komplexe Exponent oder Sinus und Cosinus) definiert ist unendliches Intervall.
3. Mit den obigen Auflistungen, die in der frei verteilten Python-Hochsprache geschrieben sind, können Sie Funktionen für Wavelets auswählen, die die angegebenen Anforderungen erfüllen. Es ist jedoch zusätzlich notwendig, alle Hauptzeichen von Wavelets zu berücksichtigen.
Die Hauptzeichen des Wavelets
Begrenztheit. Das Quadrat der Norm der Funktion muss endlich sein:
left | psi right |2= int infty− infty left| psi(t) right|2dt< infty . (2)
Lokalisierung VP verwendet im Gegensatz zur Fourier-Transformation eine lokalisierte Anfangsfunktion sowohl in der Zeit als auch in der Frequenz. Dazu reichen folgende Voraussetzungen aus:
left| psi(t) right| leqC(1+ left|t right|)−1− varepsilon und
left|S psi( omega) right| leqC(1+ left| omega right|)−1− varepsilon bei
varepsilon>0 , (3)
Zum Beispiel eine Delta-Funktion
delta(t) und harmonische Funktion erfüllen nicht die notwendige Bedingung für die gleichzeitige Lokalisierung in den Zeit- und Frequenzbereichen.
Durchschnitt Null. Der Graph der ursprünglichen Funktion sollte auf der Zeitachse um Null schwingen (abwechselnd sein) und eine Fläche von Null haben:
int infty− infty psi(t)dt=0 . (4)
Aus dieser Bedingung wird die Wahl des Namens "Wavelet" - eine kleine Welle - klar.
Gleich Null Funktionsbereich
psi(t) d.h. Null Moment führt dazu, dass die Fourier-Transformation
S psi( omega) Diese Funktion ist gleich Null für
omega=0 und hat die Form eines Bandpassfilters. Für verschiedene Werte (a) ist dies ein Satz von Bandpassfiltern.
Für Anwendungen ist es häufig erforderlich, dass nicht nur Null, sondern alle ersten n Momente gleich Null sind:
int infty− inftytn psi(t)dt=0 . (5)
Mit den n-ten Wavelets kann man die feinere (hochfrequente) Struktur des Signals analysieren und seine sich langsam ändernden Komponenten unterdrücken.
Selbst gemacht. Ein charakteristisches Merkmal von VP ist seine Selbstähnlichkeit. Alle Wavelets einer bestimmten Familie
psiab(t) haben die gleiche Anzahl von Schwingungen wie das Mutter-Wavelet
psi(t) , da daraus mittels Skalentransformationen (a) und Verschiebung (b) erhalten.
Kontinuierliche Wavelet-Transformation
Kontinuierliche (integrale) Wavelet-Transformation (NVP oder WT - kontinuierliche Wavelet-Transformation). Wir bauen die Basis
psiab(t) unter Verwendung kontinuierlicher Skalentransformationen (a) und Übertragungen (b) des Mutter-Wavelets
psi(t) mit beliebigen Werten der Basisparameter a und b in der Formel (1).
Dann werden per Definition der direkte (Analyse) und der umgekehrte (Synthese) NVP (d. H. PNVP und ONVP) des Signals S (t) wie folgt geschrieben:
Ws(a,b)=(S(t), psiab(t))= frac1 sqrta int infty− inftyS(t) psi left( fractba right)dt , (6)
S(t)= frac1C psi int infty− infty int infty− inftyWs(a,b) psiab(t) fracdadba2 , (7)
wo
C psi - Normalisierungskoeffizient,
C psi= int infty− infty left| psi( omega) right|2 left| omega right|−1d omega< inftywobei: (•, •) das Skalarprodukt der entsprechenden Faktoren ist,
mathbf psi( omega) - Fourier-Transformation eines Wavelets
psi(t) . Für orthonormale Wavelets
C psi=1 .
Aus (6) folgt das Wavelet-Spektrum
Ws(b,a) (Wavelet-Spektrum oder Zeitskalenspektrum) ist im Gegensatz zum Fourier-Spektrum (Einzelspektrum) eine Funktion von zwei Argumenten: Das erste Argument a (Zeitskala) ähnelt der Oszillationsperiode, d.h. ist invers zur Frequenz und das zweite b –– ähnelt dem Signalversatz entlang der Zeitachse.
Es sei darauf hingewiesen, dass
Ws(b,a0) charakterisiert die Zeitabhängigkeit (at
a=a0) , während die Abhängigkeiten
Ws(a,b0) es ist möglich, die Frequenzabhängigkeit anzupassen (z
b=b0 )
Wenn das untersuchte Signal S (t) ein einzelner Impuls von Dauer ist
tauu in der Nachbarschaft konzentriert
t=t0 dann hat sein Wavelet-Spektrum den größten Wert in der Nähe des Punktes mit Koordinaten
a= tauu,b=t0 .
Präsentationsmethoden Ws(b,a) kann anders sein. Spektrum
Ws(b,a) ist eine Oberfläche im dreidimensionalen Raum. Anstelle des Bildes der Oberfläche wird ihre Projektion auf die ab-Ebene jedoch häufig mit Iso-Pegeln (oder Figuren verschiedener Farben) dargestellt, die es ermöglichen, die Änderung der Intensität der EP-Amplituden in verschiedenen Maßstäben (a) und in der Zeit (b) zu verfolgen.
Darüber hinaus zeigen sie Linien lokaler Extrema dieser Oberflächen, das sogenannte Skelett (Skelett), das die Struktur des analysierten Signals aufzeigt.
Kontinuierliche Wavelet-Transformation bei der Bestimmung des Wavelet-Spektrums anhand des Mutter-Wavelets - „Mexican Hat“.
Andere für NVP verwendete mütterliche Wavelets werden ebenfalls verwendet:

Kontinuierliches VP wird häufig in der Signalverarbeitung verwendet. Insbesondere die Wavelet-Analyse (VA) bietet einzigartige Möglichkeiten, lokale und „subtile“ Merkmale von Signalen (Funktionen) zu erkennen, was in vielen Bereichen der Funktechnik, Kommunikation, Funkelektronik, Geophysik und anderen Bereichen der Wissenschaft und Technologie wichtig ist. Betrachten wir diese Möglichkeit anhand einiger einfacher Beispiele.
Harmonische Schwingung.Das Signal hat die Form:
s(t)=Asin( omegat− phi)wo:
A=1V, omega= frac2 piT= frac2 pi50, psi=0Wavelet-bildende Funktion:
MHAT(t):= fracd2dt2exp(−t2/2) ,
Wavelets:
psi(a,b,t)= frac1 sqrtaMHAT left( fract−ba right) ,
Wavelet-Spektrum: N: = 256, a: = 1..30, b: = 0..50,
W(a,b):= intN−N psi(a,b,t)s(t)dt,Nab:=W(a,b). .
Programmliste from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 T=50 def S(t): return sin(2*pi*t/T) plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,100,1)] x=[t for t in arange(0,100,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49,49) fig = plt.figure("- : ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
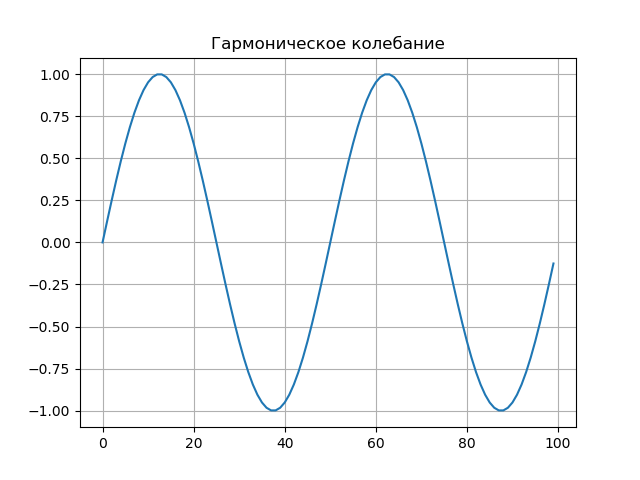
Signalgraph.

Diagramm eines Zwei-Parameter-Spektrums
Nab=W(ab) als Oberfläche im dreidimensionalen Raum angezeigt.

Es ist zu beachten, dass der Abschnitt W (a, b) für die Zeitskala
a=a0 charakterisiert die Anfangsschwingung s (t). Darüber hinaus ist seine Amplitude bei maximal
a0:1/ omega . Abhängigkeiten
W(a0,b0) kann dem aktuellen Schwingungsspektrum bei entsprechen
b=b0 .
Die Summe zweier harmonischer Schwingungen.Das Signal hat die Form:
s(t):=A1sin( omega1t)+A2sin( omega2t)wo:
A1=A2=1V, omega1= frac2 piT1, omega2= frac2 piT2,T1=50s,T2=10s .
MHAT(t):= fracd2dt2 left[e−t2/2 right] , N: = 256,
psi(a,b,t):=MHAT left( fractba right),W(a,b):= intN−N psi(a,b,t)f(t)dt , a: = 1 ... 30, b: = 0 ... 50,
Nab:=W(a,b) .
Programmliste from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): return sin(2*pi*t/10)+sin(2*pi*t/50) plt.figure(' ') plt.title(' ', size=12) y=[S(t) for t in arange(0,250,1)] x=[t for t in arange(0,250,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49, 49) fig = plt.figure("-:2- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z, 100) plt.figure() q=[w(2,i) for i in y] p=[i for i in y] plt.plot(p,q,label='w(2,b)') q=[w(15,i) for i in y] plt.plot(p,q,label='w(15,b)') q=[w(30,i) for i in y] plt.plot(p,q,label='w(30,b)') plt.legend(loc='best') plt.grid(True) plt.figure() q=[w(i,13) for i in x] p=[i for i in x] plt.plot(p,q,label='w(a,13)') q=[w(i,17) for i in x] plt.plot(p,q,label='w(a,17)') plt.legend(loc='best') plt.grid(True) plt.show()

Signalgraph.
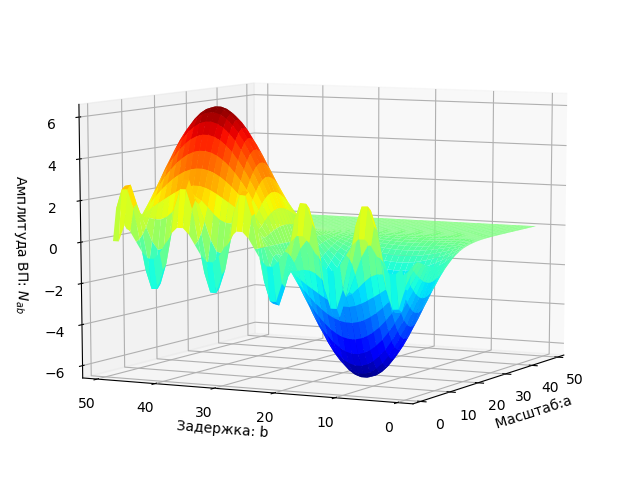
Die Darstellung des Zwei-Parameter-Spektrums W (a, b) wird als Oberfläche im dreidimensionalen Raum angezeigt.
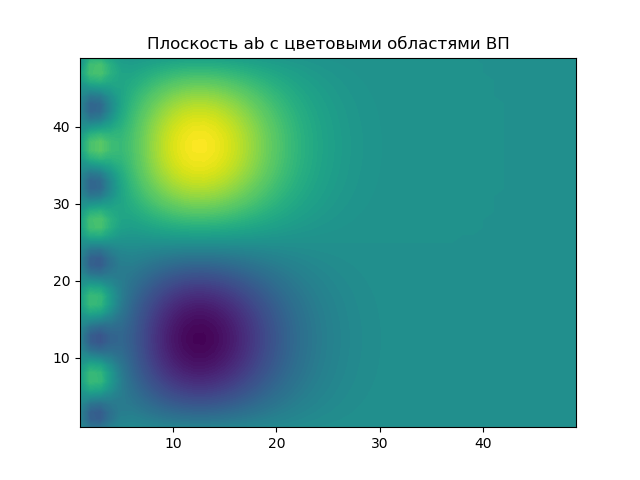
Die Ebene der Parameter a, b, auf der die Ergebnisse des EP in farbigen Bereichen hervorgehoben sind.

Die Grafik zeigt die „Querschnitte“ des Wavelet-Spektrums für zwei Werte des Parameters a. Mit einem relativ kleinen Parameter der Zeitskala a, z
a1=2(a1:1/ omega2) Der Querschnitt des Spektrums enthält nur Informationen über die Hochfrequenzkomponente des Signals, wodurch seine Niederfrequenzkomponente herausgefiltert (unterdrückt) wird.
Mit zunehmender Erweiterung der Basisfunktion
psi( fract−ba) Verengung seines Spektrums und Verengung der Bandbreite des Frequenz- "Fensters". Als Ergebnis, wenn
a2=15(a2:1/ omega1) Der Querschnitt des Spektrums ist nur eine niederfrequente Komponente des Signals.
Mit einem weiteren Anstieg von a nimmt das Fensterband immer noch ab und der Pegel dieser Niederfrequenzkomponente nimmt auf eine konstante Komponente (für a> 25) ab, die für das analysierte Signal gleich Null ist.

Die Grafik zeigt die Abschnitte des Wavelet-Spektrums W (a, b), die charakterisieren
aktuelles Signalspektrum bei
b1=13 und
b2=17 . Das Spektrum des betrachteten Signals enthält im Gegensatz zur Harmonischen eine Hochfrequenzkomponente im Bereich kleiner Werte der Zeitskala a (a: 1..3), die der zweiten Komponente des Signals entspricht
A2sin( omega2t) .
Rechteckiger Impuls.U:=5,t0:=20, tau:=60s(t):= beginvmatrixU,wennt0 leqt leqt0+ tau0,andernfalls endvmatrixMHAT(t):= fracd2dt2exp left( frac−t22 right)N:=128, psi(a,b,t):=MHAT left( fractba right),W(a,b):= intN.−N psi(a,b,t)f(t)dta:=1..50,b:=0..100,Nba:=W(a,b)Programmliste from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): U=5;t0=20;tau=60 if t0<=t<=t0+tau: return U else: return 0 plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,120,1)] x=[t for t in arange(0,120,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,100,1) y = arange(1,100,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(99, 99) fig = plt.figure("3D- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
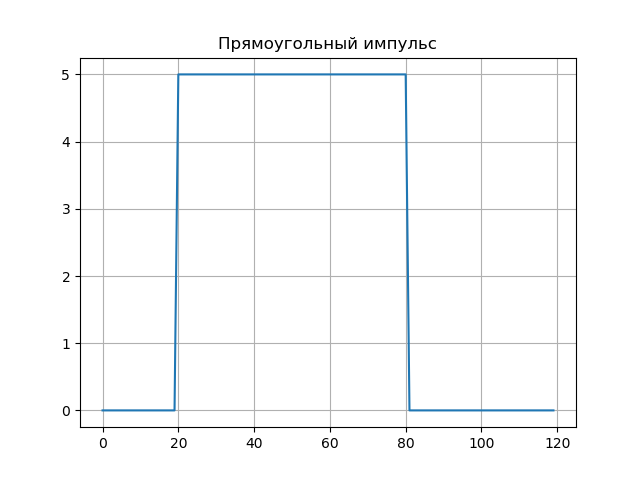


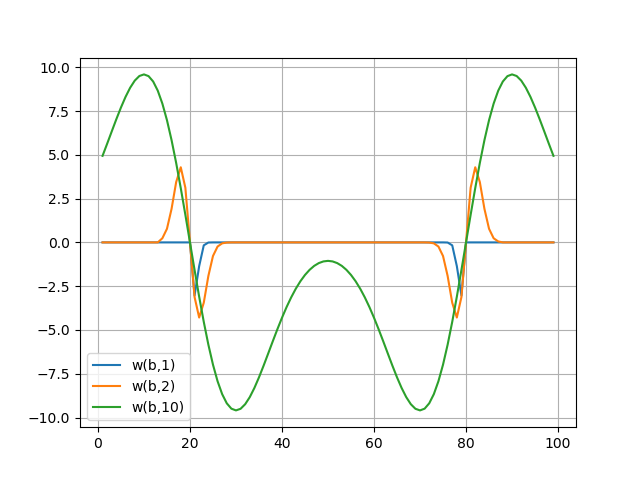
Die Wavelet-Spektren sind in Graphen dargestellt, das Wavelet-Spektrum vermittelt gut die subtilen Merkmale des Signals - seine Sprünge auf den Abtastwerten b = 20 und b = 80 (für a: 1..10).
Schlussfolgerungen
Diese Veröffentlichung ist pädagogischer Natur, enthält grundlegende Informationen zur Wavelet-Analyse im Allgemeinen und einfache Beispiele in der frei verteilten Programmiersprache Python auf hoher Ebene zeigen die Merkmale der kontinuierlichen Wavelet-Analyse mit umfassender grafischer 3D- und 2D-Visualisierung.
PS Der Autor beeinträchtigt die bedingungslosen Vorteile der Wavelet-Analyse mit Matlab sowohl hinsichtlich der Anzahl der Wavelets als auch der Geschwindigkeit nicht. In Python gibt es jedoch noch Raum für weitere Entwicklungen: scipy.signal und PyWavelets.