Jeder in der IT-Branche weiß, wie schwierig es ist , die Frist eines Projekts zu bewerten. Es ist schwierig, objektiv zu beurteilen, wie lange es dauern wird , eine schwierige Aufgabe zu lösen . Eine meiner Lieblingstheorien ist, dass dies nur ein statistisches Artefakt ist.

Angenommen, Sie bewerten ein Projekt nach 1 Woche. Angenommen, es gibt drei gleich wahrscheinliche Ergebnisse: Entweder dauert es eine halbe Woche oder eine Woche oder zwei Wochen. Das mittlere Ergebnis entspricht tatsächlich der Schätzung: 1 Woche, aber der Durchschnittswert (auch bekannt als Durchschnitt, auch bekannt als erwarteter Wert) beträgt 7/6 = 1,17 Wochen. Die Punktzahl wird tatsächlich für den Median (der 1 ist) kalibriert (unparteiisch), jedoch nicht für den Durchschnitt.

Ein vernünftiges Modell für den „Inflationsfaktor“ (tatsächliche Zeit geteilt durch geschätzte Zeit) wäre so etwas wie eine logarithmische Normalverteilung . Wenn die Schätzung einer Woche entspricht, simulieren wir das reale Ergebnis als Zufallsvariable, die gemäß der logarithmischen Normalverteilung für etwa eine Woche verteilt wird. In einer solchen Situation beträgt der Median der Verteilung genau eine Woche, aber der Durchschnittswert ist viel größer:



Wenn wir den Logarithmus des Inflationskoeffizienten nehmen, erhalten wir eine einfache Normalverteilung mit einem Zentrum von etwa 0. Dies setzt einen mittleren Inflationskoeffizienten von 1x voraus und, wie Sie hoffen, denken Sie daran, log (1) = 0. Bei verschiedenen Problemen kann es jedoch zu unterschiedlichen Unsicherheiten um 0 kommen. Wir können sie modellieren, indem wir den Parameter σ ändern, der der Standardabweichung der Normalverteilung entspricht:



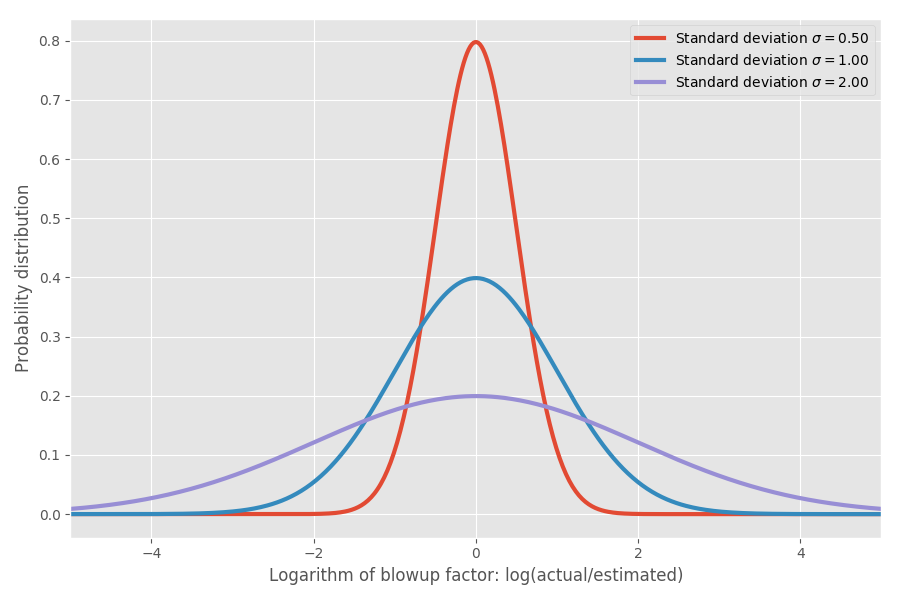
Nur um die reellen Zahlen zu zeigen: Wenn log (tatsächlich / geschätzt) = 1 ist, dann ist der Inflationskoeffizient exp (1) = e = 2,72. Es ist ebenso wahrscheinlich, dass sich das Projekt auf exp (2) = 7,4-mal erstreckt und dass es bei exp (-2) = 0,14 endet, d. H. 14% der geschätzten Zeit. Intuitiv ist der Durchschnitt so groß, weil Aufgaben, die schneller als erwartet ausgeführt werden, Aufgaben, die viel länger als erwartet dauern, nicht kompensieren können. Wir sind auf 0 beschränkt, aber nicht in die andere Richtung.

Ist das nur ein Modell? Ich wünschte du könntest! Aber bald werde ich zu den realen Daten kommen und anhand einiger empirischer Daten werde ich zeigen, dass sie tatsächlich ziemlich gut mit der Realität übereinstimmen.

Schätzung der Zeitpläne für die Softwareentwicklung

So weit, so gut, aber versuchen wir wirklich zu verstehen, was dies für die Schätzung der Zeitpläne für die Softwareentwicklung bedeutet. Angenommen, wir sehen uns einen Plan mit 20 verschiedenen Softwareprojekten an und versuchen zu bewerten, wie lange es dauern wird, bis alle abgeschlossen sind .

Hier wird der Mittelwert entscheidend. Die Durchschnittswerte summieren sich, aber es gibt keinen Median. Wenn wir uns ein Bild davon machen möchten, wie lange es dauern wird, bis die Summe von N Projekten abgeschlossen ist, müssen wir uns den Durchschnittswert ansehen. Angenommen, wir haben drei verschiedene Projekte mit demselben σ = 1:


Beachten Sie, dass sich die Durchschnittswerte addieren und 4,95 = 1,65 * 3, andere Spalten jedoch nicht.

Fügen wir nun drei Projekte mit unterschiedlichem Sigma hinzu:


Die Durchschnittswerte nehmen immer noch Gestalt an, aber die Realität entspricht nicht einmal annähernd der naiven 3-Wochen-Schätzung, die Sie erwartet haben. Beachten Sie, dass ein sehr unsicheres Projekt mit σ = 2 den Rest der durchschnittlichen Fertigstellungszeit dominiert . Und für das 99. Perzentil dominiert es nicht nur, sondern absorbiert buchstäblich alle anderen. Wir können ein größeres Beispiel geben:


Auch hier dominiert die einzige unangenehme Aufgabe hauptsächlich bei der Berechnung der Schätzung, zumindest in 99% der Fälle. Selbst in der Durchschnittszeit benötigt ein verrücktes Projekt letztendlich etwa die Hälfte der Zeit, die für alle Aufgaben aufgewendet wird, obwohl sie im Median ähnliche Werte haben. Der Einfachheit halber habe ich angenommen, dass alle Aufgaben dieselbe Zeitschätzung, aber unterschiedliche Unsicherheiten haben. Mathematik wird gespeichert, wenn sich die Begriffe ändern.

Es ist lustig, aber ich habe dieses Gefühl schon lange gehabt. Das Hinzufügen von Bewertungen funktioniert selten, wenn Sie viele Aufgaben haben. Finden Sie stattdessen heraus, welche Aufgaben die höchste Unsicherheit aufweisen: Diese Aufgaben dominieren normalerweise die durchschnittliche Ausführungszeit.

Das Diagramm zeigt den Mittelwert und das 99. Perzentil als Funktion der Unsicherheit (σ):



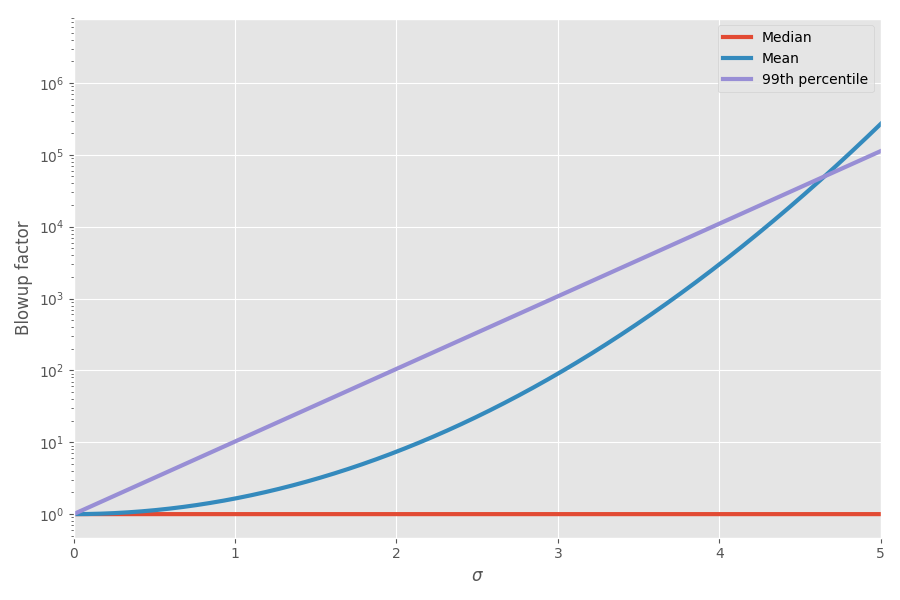
Jetzt erklärte Mathe meine Empfindungen! Ich begann dies bei der Planung von Projekten zu berücksichtigen. Ich denke wirklich, dass das Hinzufügen von Schätzungen der Fristen für die Aufgaben sehr irreführend ist und ein falsches Bild davon erzeugt, wie viel Zeit das gesamte Projekt in Anspruch nehmen wird, da Sie diese verrückten verzerrten Aufgaben haben, die letztendlich die ganze Zeit in Anspruch nehmen.

Wo sind die empirischen Beweise?

Lange Zeit habe ich es in der Rubrik „Neugierige Spielzeugmodelle“ in meinem Gehirn behalten und manchmal gedacht, dass dies eine gute Illustration des Phänomens der realen Welt ist. Aber eines Tages, als ich durch das Netzwerk wanderte, stieß ich auf interessante Daten zur Bewertung des Zeitpunkts von Projekten und der tatsächlichen Zeit, um sie abzuschließen. Fiktion!

Lassen Sie uns ein kurzes Streudiagramm der geschätzten und tatsächlichen Zeit erstellen:



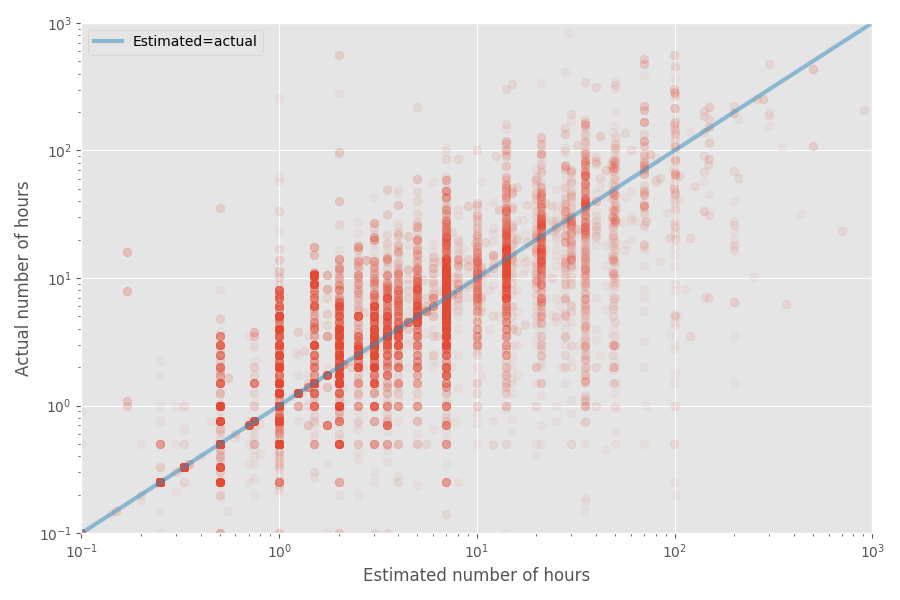
Die mittlere Inflationsrate für diesen Datensatz beträgt 1X, während der durchschnittliche Koeffizient 1,81x beträgt. Dies bestätigt erneut die Vermutung, dass die Entwickler den Median gut bewerten, der Durchschnitt jedoch viel höher ist.

Schauen wir uns die Verteilung des Inflationskoeffizienten (Logarithmus) an:



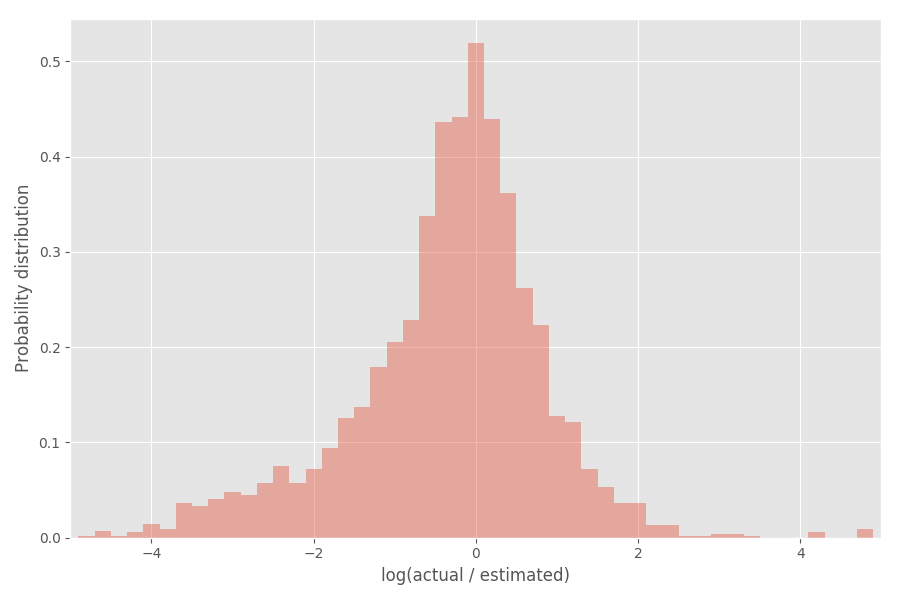
Wie Sie sehen können, ist es ziemlich gut um 0 zentriert, wobei der Inflationskoeffizient exp (0) = 1 ist.

Nehmen Sie die statistischen Werkzeuge

Jetzt werde ich mir ein wenig mit Statistiken ausdenken - zögern Sie nicht, diesen Teil zu überspringen, wenn er für Sie nicht interessant ist. Was können wir aus dieser empirischen Verteilung schließen? Sie können erwarten, dass die Logarithmen der Inflationsrate gemäß der Normalverteilung verteilt werden, aber dies ist nicht ganz richtig. Beachten Sie, dass σ selbst zufällig ist und für jedes Projekt variiert.

Eine bequeme Methode zur Modellierung von σ besteht darin, dass sie aus der inversen Gammaverteilung ausgewählt werden . Wenn wir (wie zuvor) annehmen, dass der Logarithmus der Inflationskoeffizienten gemäß der Normalverteilung verteilt ist, endet die "globale" Verteilung der Logarithmen der Inflationskoeffizienten mit der Student-Verteilung .

Wir wenden die Studentenverteilung auf die vorherige an:



Anständig konvergiert meiner Meinung nach! Schülerverteilungsparameter bestimmen auch die inverse Gammaverteilung von σ-Werten:



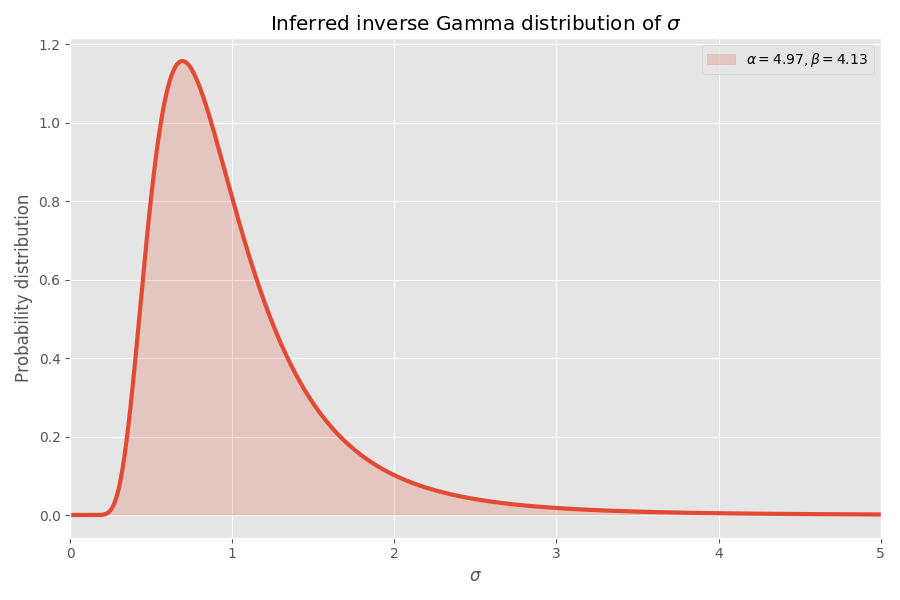
Beachten Sie, dass Werte von σ> 4 sehr unwahrscheinlich sind, aber wenn sie auftreten, verursachen sie eine durchschnittliche Explosion von mehreren tausend Mal.

Warum Software-Aufgaben immer länger dauern als Sie denken

Unter der Annahme, dass dieser Datensatz für die Softwareentwicklung repräsentativ ist (zweifelhaft!), Können wir einige weitere Schlussfolgerungen ziehen. Wir haben Parameter für die Schülerverteilung, sodass wir die durchschnittliche Zeit berechnen können, die zum Ausführen der Aufgabe erforderlich ist, ohne σ für diese Aufgabe zu kennen.

Während die mittlere Inflationsrate aus dieser Anpassung 1x (wie zuvor) beträgt, beträgt die Inflationsrate von 99% 32x, aber wenn Sie zum 99,99-Perzentil gehen, sind es satte 55 Millionen ! Eine (freie) Interpretation ist, dass einige Aufgaben letztendlich unmöglich sind. Tatsächlich haben diese extremen Fälle einen so großen Einfluss auf den Durchschnitt, dass die durchschnittliche Inflationsrate einer Aufgabe unendlich wird . Das sind ziemlich schlechte Nachrichten für alle, die versuchen, Termine einzuhalten!

Zusammenfassung

Wenn mein Modell korrekt ist (großes Wenn), können wir Folgendes herausfinden:

• Die Leute schätzen die mittlere Zeit für die Erledigung einer Aufgabe gut ein, aber nicht den Durchschnitt.
  
• Die durchschnittliche Zeit ist viel größer als der Median, da die Verteilung verzerrt ist (logarithmische Normalverteilung).
  
• Wenn Sie Noten für n Aufgaben hinzufügen, wird es schlimmer.
  
• Aufgaben mit der größten Unsicherheit (eher mit der größten Größe) können häufig in der durchschnittlichen Zeit dominieren, die erforderlich ist, um alle Aufgaben zu erledigen.
  
• Die durchschnittliche Ausführungszeit einer Aufgabe, von der wir nichts wissen, ist tatsächlich unendlich .

Anmerkungen

• Offensichtlich basieren die Ergebnisse nur auf einem Datensatz, den ich im Internet gefunden habe. Andere Datensätze können zu anderen Ergebnissen führen.
  
• Mein Modell ist natürlich auch sehr subjektiv, wie jedes statistische Modell.
  
• Ich würde das Modell gerne auf einen viel größeren Datensatz anwenden, um zu sehen, wie stabil es ist.
  
• Ich schlug vor, dass alle Aufgaben unabhängig sind. Tatsächlich haben sie möglicherweise eine Korrelation, die die Analyse viel ärgerlicher macht, aber (glaube ich) zu ähnlichen Schlussfolgerungen führt.
  
• Die Summe der logarithmisch normalverteilten Werte ist kein weiterer logarithmisch normalverteilter Wert. Dies ist die Schwäche dieser Verteilung, da Sie argumentieren können, dass die meisten Aufgaben einfach die Summe der Unteraufgaben sind. Es wäre schön, wenn unser Vertrieb nachhaltig wäre .
  
• Ich habe kleine Aufgaben aus dem Histogramm gelöscht (die geschätzte Zeit beträgt höchstens 7 Stunden), da sie die Analyse verzerren und es einen merkwürdigen Anstieg von genau 7 gab.
  
• Der Code ist wie üblich auf Github .