Guten Tag, lieber Leser! Dies ist der zweite übersetzte Artikel in einer Reihe von Artikeln über die Erstellung der Physik-Engine von Chris Hecker. Wenn Sie sich noch nicht mit dem ersten vertraut gemacht haben, empfehle ich dies, da alles sofort klar wird. Vielen Dank für die Unterstützung der ersten Übersetzung: Es ist sehr ermutigend, weiter und mehr zu arbeiten! Viel Spaß beim Lesen!

Physik, Teil 2, Winkeleffekte

Ich wollte nur die Tür mit etwas Schwerem hinter mir lassen, damit kein Eindringling hereinkommt. Frage ich viel Ich möchte, dass sein Auto an einem bestimmten Ort überrollt und explodiert. Ich möchte, dass die riesigen Zahnräder blockieren, bevor sie mich platt machen. Und ich möchte hastig etwas bauen, das wie eine Schaukel aussieht, um ein süßes leuchtendes Geschenk durch die Festungsmauer des Schlosses zu katapultieren. Wer kann mich davon abhalten, all dies in die Realität umzusetzen? Sie nehmen an, dass mein Gegner in der Spielwelt ist, aber in Wirklichkeit - ein Programmierer der physischen Engine, weil all das auf dem Winkeleffekt basiert. Sie können sich auf die Finger der Spiele verlassen, in denen Eckeneffekte implementiert sind, ganz zu schweigen davon, mindestens eines zu finden, in dem dies korrekt durchgeführt wird.

Der Hauptgrund, warum Winkeleffekte (oder andere Rotationseffekte) heutzutage in Spielen nicht implementiert werden, liegt darin, dass Programmierer der Ansicht sind, dass die Physik, die die Rotationsbewegung beschreibt, zu kompliziert ist, um sie zu verstehen und in die Realität umzusetzen. Im Physikunterricht an der High School (wo wir alle Newtons zweites Gesetz gelernt haben) sprechen sie normalerweise nicht über Rotationseffekte, und es ist nicht ganz offensichtlich, wie man sich von der auf das Objekt ausgeübten Kraft zur Rotation dieses Objekts bewegt. Natürlich ist die Dynamik der Rotationsbewegung etwas schwieriger zu verstehen als die Dynamik der linearen Bewegung, aber sie ist einfacher als es scheint. Jeder, der einen physischen Motor gemäß dem im ersten Artikel des Zyklus vorgestellten Material erstellen kann, kann auch die in diesem Artikel beschriebenen Winkeleffekte berücksichtigen. Es ist zu hoffen, dass nach der Veröffentlichung dieses Artikels die Welt mit Spielen gefüllt sein wird, die alle Möglichkeiten und Vorteile von Eckeneffekten nutzen, oder zumindest können Sie ein Spiel erstellen, in dem Sie Ihren Freund in einem tödlichen Kampf ins Bein schießen, wenn Sie sich bücken.

Kurze Wiederholung

Trotz der Tatsache, dass jeder meiner Artikel ein einzigartiges Thema hat, habe ich immer wieder gelesen, was ich zuvor geschrieben habe, um zu verstehen, wo ich gelandet bin. Ich habe gerade meinen ersten Artikel über Physik gesehen und bin begeistert: Wir haben so viel gelernt und außerdem haben wir nie einen Programmcode geschrieben oder zusätzliche Literatur gelesen! Bevor wir beginnen, aktualisieren wir das Material aus dem letzten Artikel.



Tabelle 1 enthält die wichtigsten Schlussfolgerungen für die Dynamik von Festkörpern. Aus Gleichung 1 folgt, dass der Koordinatenvektor (r), der Geschwindigkeitsvektor (v) und der Beschleunigungsvektor (a) durch Ableitungen (und durch Integrale, wenn wir in umgekehrter Reihenfolge lesen) in Beziehung stehen. Zur Erinnerung, wir markieren die Zeitdifferenzierung durch eine Primzahl (r '). r 'ist dasselbe wie dr / dt und r' 'ist dasselbe wie die zweite Zeitableitung. Aus Gleichung 2 folgt, dass die Kraft mit einem linearen Impuls (dem Produkt aus Masse und Geschwindigkeit), Masse und Beschleunigung verbunden ist. Die Definition des Massenschwerpunkts kann aus Gleichung 3 erhalten werden (dies ist der Punkt, an dem sich alle Massen und Abstände ausgleichen). Gleichung 4 besagt, dass der gesamte lineare Impuls eines Festkörpers die Summe aller seiner Impulse ist, die zu unserem Glück einfach gleich dem Impuls des Massenschwerpunkts (CM) sind. Gleichung 5 ist ein echtes Juwel. Es verwendet Gleichung 4, um zu demonstrieren, dass die Beschleunigung des Massenschwerpunkts eines Objekts mit der Gesamtkraft (dem Vektor der Summe aller Kräfte, die zu einem bestimmten Zeitpunkt auf das Objekt wirken) durch eine skalare Größe, die Masse des Objekts, in Beziehung steht.

Um alles zusammenzufassen, was im ersten Artikel beschrieben wurde: Wir haben gelernt, dass die Gesamtkraft, die auf unseren Schwerpunkt wirkt, gleich der Summe aller auf den Körper ausgeübten Kräfte ist (einschließlich der Schwerkraft, des Wagens des Bösewichts, einer Explosion in der Nähe, des Schubes unseres Motors usw.). .). Danach haben wir diesen Summenvektor durch die Körpermasse geteilt, um die CM-Beschleunigung zu erhalten, und dann die Zeitbeschleunigung integriert, um die Geschwindigkeit und Koordinate des Körpers zu erhalten.

Gleichung 5 ist nur ein Meisterwerk! Sie werden sehen, dass es darin kein Konzept für Angriffspunkte von Kräften auf den Körper gibt, und dies ist ein Schlüsselpunkt bei der Bestimmung, wie sich der Körper unter seiner Wirkung dreht. Gleichung 5 ist korrekt. Tatsächlich eignet es sich hervorragend zum Auffinden einer linearen Beschleunigung. Wir vermissen die halbe Miete. Aber das Wichtigste zuerst ...

Was ist dein Winkel?

Im ersten Artikel wurde die Rotation ignoriert, sodass wir nur einen Radiusvektor und seine Ableitung benötigten, um die Konfiguration unseres Körpers in 2D zu beschreiben. Fügen wir nun einen weiteren kinematischen Wert hinzu, die Orientierung (gekennzeichnet durch den Großbuchstaben Omega - Ω), um mit Eckeneffekten zu arbeiten. Um Ω einzustellen, müssen wir das Koordinatensystem relativ zum Volumenkörper und zum Koordinatensystem der Spielwelt auswählen. Der Wert von Ω entspricht der Winkeldifferenz zwischen ihnen im Bogenmaß, wie in Abbildung 1 dargestellt.



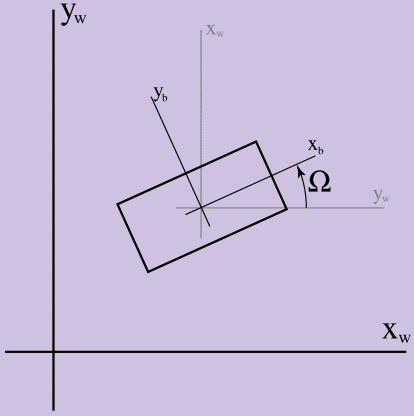Abbildung 1. Definition von Ω

In der Figur sind die xw, yw-Achsen die Koordinatenachsen der Spielwelt und xb, yb die Koordinatenachsen des Volumenkörpers. Ω ist größer als 0, wenn gegen den Uhrzeigersinn gezählt wird. Hier ist es wichtig zu klären, warum wir die Dynamik der zweidimensionalen Welt untersuchen, bevor wir zur dreidimensionalen Welt übergehen: Die Orientierung in 2D ist eine skalare Größe (der Winkel zwischen Koordinatensystemen im Bogenmaß), während die Bestimmung der Orientierung in der dreidimensionalen Welt viel schwieriger ist.

Wenn sich der Körper dreht, ändert sich der Wert von Ω. Diese Änderung führt uns zu einer anderen Kinematik - der Winkelgeschwindigkeit (bezeichnet durch den Kleinbuchstaben Omega - ω). Im Gegensatz zur Koordinaten- und Lineargeschwindigkeit des Körpers bezeichnen wir die Winkelgeschwindigkeit nicht wie folgt - Ω '. Manchmal bezeichnen wir jedoch die Ableitung der Geschwindigkeit in Bezug auf die Zeit oder die Winkelbeschleunigung als ω '(dies ist ein anderer kinematischer Wert) oder als α (Kleinbuchstaben alpha). Beschuldigen Sie mich nicht: Ich habe mir nicht alle diese Bezeichnungen ausgedacht; und in jedem Buch, das ich lese, gibt es leichte Abweichungen. Unser eckiges Gegenstück zu Gleichung 1 ist:

$$$$ Anzeige $$ {d ^ 2 Ω \ über {dt ^ 2}} = {dω \ über {dt}} = ω '= α $$ Anzeige $$

Gleichung 6

Wie in Gleichung 1 differenzieren wir ω zeitlich, um α zu erhalten; und wenn wir α über die Zeit integrieren, erhalten wir ω usw. Alles in Analogie zum vorherigen Artikel: Wenn wir die Winkelbeschleunigung von α kennen, können wir es zweimal integrieren, um eine neue Orientierung zu erhalten. Der entscheidende Punkt hierbei ist jedoch, den Wert von α zu kennen.

Wie Sie sich vorstellen können, besteht unser Ziel für diesen Artikel darin, für jede der linearen Gleichungen in Tabelle 1 ein Winkelanalogon abzuleiten. Anschließend können wir unter Berücksichtigung der linearen und Winkelgleichungen und der auf das Objekt ausgeübten Kraft die lineare Beschleunigung a und die Winkelbeschleunigung α berechnen. Schließlich können wir diese Beschleunigungen numerisch integrieren, um neue Positionen und Orientierungen unseres Körpers zu finden.

Zunächst werden wir lineare und Winkelgrößen miteinander verbinden. Und dies ist ein ziemlich offensichtlicher Trick, bei dem die Winkelgeschwindigkeit verwendet wird. Bei der Berechnung der Dynamik müssen wir häufig die Geschwindigkeit eines beliebigen Punkts auf einem Objekt ermitteln. Wenn wir beispielsweise Kollisionen von Festkörpern berechnen, müssen wir die Geschwindigkeit der Kollisionspunkte kennen, um zu verstehen, wie stark sie aufeinander treffen. Wenn sich unser Körper nicht dreht, ist die Geschwindigkeit jedes Punktes des Körpers gleich. Wir können einfach die Geschwindigkeit des Massenschwerpunkts des Körpers überwachen, und das wird ausreichen. Wenn sich unser Körper dreht, kann jeder Punkt dieser Körper eine andere Geschwindigkeit haben. Offensichtlich können wir die Geschwindigkeit einer unendlichen Anzahl von Punkten unseres starren Körpers nicht berechnen, deshalb brauchen wir eine andere, bessere Lösung.

Eine der einfachen Methoden, mit denen die Lineargeschwindigkeit eines beliebigen Punkts innerhalb eines Objekts ermittelt wird, verwendet die Winkelgeschwindigkeit des Objekts. Betrachten Sie den Fall, in dem sich der Körper nur um einen festen Punkt O dreht, ohne die Koordinate des Körpers zu ändern. Das heißt, der Körper dreht sich, bewegt sich aber nicht. Aus Gleichung 7 folgt, wie die Geschwindigkeit von Punkt B eines rotierenden Körpers berechnet wird:

$$$$ Anzeige $$ v ^ B = ωr ^ {OB} _⟂ $$ Anzeige $$

Gleichung 7

Wir müssen einige Punkte in Gleichung 7 klarstellen, lassen Sie uns etwas Zeit damit verbringen. Zuerst benutze ich die Top-Indizierung, um zu zeigen, welcher Parameter zu diesen Punkten gehört, also ist v ^ B der Geschwindigkeitsvektor von Punkt B unseres Körpers. In ähnlicher Weise bezeichnet r ^ OB einen Vektor, der vom Rotationszentrum unseres Körpers O zum Punkt B gezogen wird. Der lustige umgekehrte Buchstabe T ist der „senkrechte Operator“, der auf den Vektor wirkt (wie der Vektor r in Gleichung 7) und ihn um 90 Grad gegen den Uhrzeigersinn dreht Pfeile. Mit anderen Worten wird ein neuer Vektor konstruiert, der senkrecht zum alten ist. In einer zweidimensionalen Welt ist ein Vektor senkrecht zu (x, y) nur (-y, x). Sie können meine Wörter leicht auf einem Millimeterpapierblatt überprüfen. Reden wir mehr darüber. Die Größe des senkrechten Vektors wird durch die Winkelgeschwindigkeit ω bestimmt und setzt die Lineargeschwindigkeit v ^ B. Im Russischen zeigt Gleichung 7, dass die Geschwindigkeit eines Punktes eines rotierenden Körpers berechnet wird, indem der vom Rotationszentrum gezogene senkrechte Vektor mit der Winkelgeschwindigkeit multipliziert wird. Wie verstehe ich das? Nun, ich habe darüber im Buch gelesen, aber es ist offensichtlich, dass eine solche Erklärung nicht ausreicht, also beweisen wir, dass dies wahr ist.

Lassen Sie uns die Wahrheit der Schlussfolgerungen von Gleichung 7 in zwei Stufen beweisen. Zunächst beweisen wir, dass der Wert des resultierenden Geschwindigkeitsvektors korrekt ist; dann - dass seine Richtung richtig ist. Betrachten Sie für den ersten Teil des Beweises Abbildung 2.



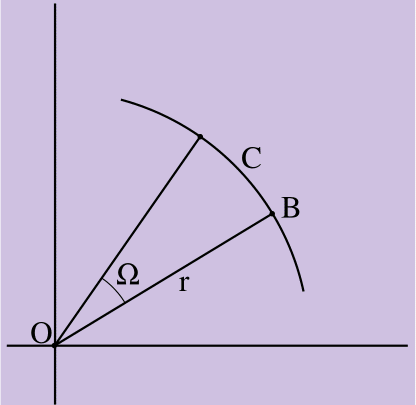Abbildung 2. C = Ωr

Fig. 2 zeigt die Drehung von Punkt B um einen Winkel von Ω Radiant entlang der Drehung eines starren Körpers mit einem Radiusvektor der Länge r, der vom Rotationszentrum des Körpers O zum Punkt B gerichtet ist. B passierte die Länge des Bogens C, wobei C = Ωr aus der Definition des Bogenmaßes. (Ein Bogenmaß eines Winkels ist ein Maß eines Bogens, der durch einen Radius eines Kreises begrenzt ist. Der Umfang eines Kreises beträgt C = 2πr, da das Bogenmaß eines Kreisbogens 2π [oder 360 Grad] beträgt.)

Die Geschwindigkeit eines Punktes ist eine Änderung seiner zeitlichen Koordinate. Daher können wir die Geschwindigkeit von Punkt B - mit anderen Worten die Größe des Geschwindigkeitsvektors - durch Differenzieren der Bewegungsgleichungen in Bezug auf die Zeit ermitteln. C = Ωr ist die Bewegungsgleichung.

$$

$${d (Ωr) \ über {dt}} = {dΩ \ über {dt}} r = ωr$$

Der Radius wird aus dem Differenzierungszeichen herausgenommen, da er eine Konstante ist (Punkt B dreht sich einfach ohne lineare Verschiebung) und die Zeitableitung Ω aus Gleichung 6 ω ist. Daher ist die Größe des Vektors B der Geschwindigkeitsvektor ωr.

Wenn wir Gleichung 7 betrachten, stellen wir fest, dass die Größe des Geschwindigkeitsvektors korrekt ist, da die Senkrechte die Länge des Vektors nicht beeinflusst und r ^ OB ein Radiusvektor ist, der von O nach B gerichtet ist. Fuh, wir sind auf halbem Weg.

Um zu überprüfen, ob die Richtung des Geschwindigkeitsvektors in Gleichung 7 korrekt ist, stellen wir zunächst sicher, dass der Geschwindigkeitsvektor senkrecht zum Radiusvektor sein muss. Diese Annahme ist intuitiv verständlich, da sich ein Punkt, der sich um einen anderen bestimmten Punkt dreht, nur senkrecht zum Vektor zwischen diesen Punkten bewegen kann. Es kann sich dem Rotationszentrum nicht nähern oder sich von diesem entfernen, oder diese Bewegung hört einfach auf, Rotation zu sein. Wir können unsere Annahme mit Berechnungen für Vektoren unterstützen, aber ich bin in einem bestimmten Rahmen für das Volumen des Artikels festgeklemmt, sodass wir davon ausgehen werden, dass unsere Annahme korrekt ist. (Wenn Sie dies selbst beweisen möchten, differenzieren Sie das Skalarprodukt eines Vektors fester Länge von selbst.)

Schließlich müssen wir sicherstellen, dass der Vektor korrekt markiert ist, da die Abbildung zwei Vektoren gleicher Länge senkrecht zum Radius zeigt: v und -v. Da der Wert von Ω gegen den Uhrzeigersinn gemessen wird, ist ω> 0, wenn sich der Punkt im Uhrzeigersinn dreht. Die Senkrechte zeigt im Uhrzeigersinn, ebenso wie der Radiusvektor. 3 zeigt die Schlussfolgerungen aus Gleichung 7:



Abbildung 3. Beziehung zwischen Lineargeschwindigkeit und Winkel

Ergänzen Sie Gleichung 7, um die Drehung von sich bewegenden Körpern zu beschreiben. Wir betrachten die Bewegung eines festen Körpers als eine einfache Bewegung des Rotationszentrums des Körpers und eine einfache Rotation des restlichen Körpers um diesen Punkt. Für Interessierte ist dies der Schal-Satz zur Klassifikation von Bewegungen.

Der Satz von Chall unterteilt unsere Bewegung in zwei Komponenten - linear und eckig. Sei das Rotationszentrum des Körpers O der einzige Bewegungspunkt, dann verwenden wir ω, um die Rotation um den Punkt O zu berechnen, und dies gibt uns die allgemeine Form von Gleichung 7:

$$$$ Anzeige $$ v ^ B = v ^ O + ωr ^ {OB} _⟂ $$ Anzeige $$

Gleichung 9

Gleichung 9 besagt, dass wir die Geschwindigkeit eines beliebigen Punktes eines sich bewegenden Körpers unter Verwendung der linearen Geschwindigkeit des Rotationszentrums des Körpers und zusätzlich der Geschwindigkeit berechnen können, die während der Rotation des Körpers erfasst wird.

Grund für unseren Impuls

Jetzt können wir ein Winkelanalogon von Gleichung 2, der Kraftgleichung, schreiben. Wir beginnen mit der Bestimmung des Drehimpulses L ^ AB eines gegebenen Punktes B um einen anderen Punkt A:

$$

$${L} ^ {AB} = {\ vec r} ^ {AB} \ times {\ vec p} ^ B$$

Gleichung 10

Das Impulsmoment eines Punktes unterscheidet sich vom linearen Impuls eines Punktes darin, dass die Winkelversion der Gleichung die Position des Körpers im Raum berücksichtigt. Daraus folgt, dass der Drehimpuls eines Punktes für einen anderen Ort in der Spielwelt gemessen werden muss, im Gegensatz zu dem linearen Impuls, der für einen bestimmten Punkt (das Produkt seiner Masse und Geschwindigkeit) bestimmt wird. Dies wird durch die obere Indexierung in Gleichung 10 gezeigt. Die Notation L ^ AB besagt, dass der Drehimpuls für Punkt B von Punkt A (Rotationszentrum des Körpers) gemessen wird. Stellen Sie sich einen Pfeil vor, der von Punkt A nach Punkt B zeigt. Dieser Pfeil ist ein Radiusvektor zwischen zwei Punkten und bedeutet r ^ AB. Der Drehimpuls eines Punktes ist also ein Skalarprodukt eines linearen Impulsvektors und eines Radiusvektors senkrecht dazu. Diese Operation wird als "Skalarprodukt mit Senkrechten" bezeichnet und ist ein 2D-Analogon für das 3D-Vektorprodukt. Wir werden sie jedoch ein anderes Mal diskutieren.

Wenn Sie das, was aus Gleichung 10 folgt, auf Papier grafisch darstellen - wie ich es in Abbildung 4 getan habe -, werden Sie sehen, dass es das Maß dafür bestimmt, wie sich das lineare Moment von Punkt B um A dreht.



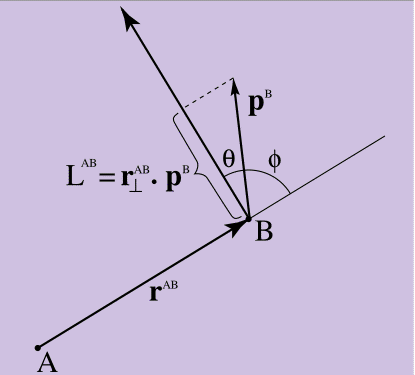Abbildung 4. Impulsmoment

Alles ist korrekt, wenn der Impuls von Punkt B direkt auf Punkt A zeigt, Gleichung 10 = 0 (da die Senkrechte zu r mit p einen rechten Winkel bildet und das Skalarprodukt 0 ist). Je größer der Impuls B ist, der senkrecht zu A gerichtet ist, desto größer ist der Impuls. Wie in 4 zu sehen ist, hat das Skalarprodukt in Gleichung 10 als Parameter den Kosinus des Winkels & thgr;, der zwischen der Senkrechten r ^ AB zu p ^ B eingeschlossen ist. Wenn Sie es andererseits betrachten, ist die Größe des Skalarprodukts durch den Sinus des Winkels φ zwischen dem Original und nicht senkrecht r ^ AB und p ^ B gegeben (Sinus ist ein weiterer Schlüssel zum Aufdecken der Verbindung zwischen dem Vektor und dem Skalarprodukt). Gleichung 10 gibt ein Maß dafür, wie viel des Impulses von Punkt B in der "Drehrichtung" relativ zu Punkt A "aussieht".

Da wir die Ableitung des linearen Impulses zur Bestimmung der Kraft verwendet haben, werden wir auch die Ableitung des Drehimpulses verwenden, um den Winkelzwilling der Kraft zu bestimmen - das Moment der Kraft (angezeigt durch den Kleinbuchstaben tau - τ).

$$

$$τ ^ {AB} = {dL ^ {AB} \ über dt} = {d ({\ vec r} ^ {AB} \ mal {\ vec p} ^ B) \ über dt} = \ vec r ^ { AB} \ times ma ^ B = \ vec r ^ {AB} \ times F ^ B$$

Gleichung 11

Um Platz zu sparen, habe ich in Gleichung 11 ein wenig geschummelt und einige schwierige Schritte übersprungen, bei denen Ableitungen gefunden wurden. Aus dem Vorstehenden folgt, dass das Kraftmoment mit der Kraft an einem bestimmten Punkt durch ein Skalarprodukt verbunden ist.

Schließlich haben wir eine dynamische Gleichung erhalten, die den Kraftangriffspunkt verwendet, der zuvor in den linearen Impulsgleichungen ignoriert wurde. Gleichung 11 verwendet ein Skalarprodukt mit einer Senkrechten als Maß dafür, wie viel der auf Punkt B ausgeübten Kraft sich um Punkt A dreht; Diese „Rotationskraft“ wird als Kraftmoment bezeichnet. Mit Gleichung 11 können Sie den numerischen Wert des Kraftmoments ermitteln - und damit den Drehimpuls, wenn wir das Kraftmoment integrieren und die aufgebrachte Kraft und den Angriffspunkt kennen.

Wir haben jedoch immer noch nicht die Gleichung der Beziehung zwischen dem Kraftmoment und den Winkelgrößen der Kinematik erhalten, die wir benötigen, um das Objekt um seine Achse zu drehen - wie Winkelbeschleunigung, Winkelgeschwindigkeit oder Orientierung. Daher können wir nicht vorwärts gehen, bevor wir einige weitere Gleichungen abgeleitet haben.

Der Moment, auf den wir alle gewartet haben

Bevor wir eine Verbindung zwischen Dynamik und Kinematik herstellen, müssen wir den Gesamtdrehimpuls in Analogie zu der Bestimmung des Gesamtlinearimpulses in Gleichung 4 bestimmen. Ich habe das Winkeläquivalent für den Schwerpunkt in Gleichung 3 nicht vergessen. wir werden es in der Gleichung des gesamten Drehimpulses sehen.

Der Gesamtdrehimpuls in der Nähe von Punkt A wird mit L ^ AT bezeichnet und durch Gleichung 12 bestimmt:

$$

$$L ^ {AT} = {\ sum _ {i} {} {\ vec r ^ {Ai} \ times p ^ i}} = {\ sum _ {i} {\ vec r ^ {Ai} \ times m ^ iv ^ i}}$$

Gleichung 12

Gleichung 12 ist die Summe aller Drehimpulse aller Körperpunkte, gemessen relativ zu Punkt A. Auf der rechten Seite habe ich die Definition des linearen Impulses verwendet, um p ^ i als Produkt von Masse und Geschwindigkeit (mv) darzustellen. Dies wird mir in Zukunft nützlich sein, um aus Gleichung 12 etwas mit einem ausgeprägteren angewandten Charakter zu machen. Die Gleichung besagt, dass es notwendig ist, den Drehimpuls aller seiner Punkte zu summieren, um den Gesamtdrehimpuls für unser Objekt zu ermitteln. Für einen festen Körper, der aus Flächen besteht (und nicht aus getrennten Punkten), muss das Integral für eine nicht diskrete Summe berechnet werden.

Glücklicherweise können wir unsere Berechnungen vereinfachen, indem wir eine neue Größe einführen, die als "Trägheitsmoment" bezeichnet wird, ähnlich wie wir den Schwerpunkt eingeführt haben, um die Gesamtimpulsgleichung zu vereinfachen. Denken Sie daran, dass wir dank Gleichung 7 die Geschwindigkeit eines Punktes durch die Winkelgeschwindigkeit ermitteln können. Sei Punkt A in Gleichung 12 das Rotationszentrum von Gleichung 7 und der Summationsindex i in Gleichung 12 Punkt B von Gleichung 7, dann ist es möglich, Gleichung 7 in Gleichung 12 umzuwandeln. Wir erhalten:

$$

$$L^{AT} = \sum _{ i} {\vec r ^{Ai} \times m^i ω \vec r^{Ai}} = ω {\sum _{ i} {m^i \vec r^{Ai} \times \vec r ^{Ai}}} = ω \sum_{ i} {m^i (\vec r ^{Ai})^2} = ωI^A$$

Gleichung 13 Ich werde

Gleichung 13 Schritt für Schritt genauer aufschreiben. Zuerst ersetzen wir Gleichung 7 durch 12, um die Summe in Gleichung 13 zu erhalten. Diese Ersetzung ermöglicht es uns, den Drehimpuls unter Verwendung der Winkelgeschwindigkeit zu beschreiben. Als nächstes nehmen wir ω für die Summe, weil es für alle Punkte des Festkörpers gleich ist (die Winkelgeschwindigkeit wird für den gesamten Körper und nicht für jeden Punkt separat bestimmt), und schreiben die Masse mit dem Index i links auf, um das Skalarprodukt klarer zu sehen -vektoren für sich. Dieses Skalarprodukt ist gleich dem Quadrat der Länge des Radiusvektors (das Skalarprodukt eines Vektors für sich = das Quadrat seiner Länge. Denken Sie daran, dass der senkrechte Operator die Länge des Vektors nicht ändert.). Schließlich schreiben wir I ^ A, um das Trägheitsmoment um Punkt A zu bezeichnen.

Das Trägheitsmoment für einen zweidimensionalen Festkörper ist eine äußerst gute Zahl, da die Punkte, aus denen der Körper besteht, ihre Masse nicht ändern oder sich nicht vom Rotationszentrum entfernen können. Infolge dieser beiden Eigenschaften ist die Summe in Gleichung 13 eine Konstante für jeden Körper, sodass wir sie berechnen können. In russischer Sprache ist I ^ A die Summe der Abstände im Quadrat von Punkt A zu allen anderen Punkten des Körpers, und jeder dieser Abstände wird entsprechend der Masse jedes Punktes skaliert. Genau wie beim Schwerpunkt - wenn der Körper fester ist als aus diskreten Punkten zusammengesetzt, werden die Summen zu Integralen. Und das Trägheitsmoment wird in seiner Größe gleich bleiben und dieselbe physikalische Bedeutung haben.

Die Bestimmung des Trägheitsmoments in der Nähe eines Punktes ist ausführlich, aber stellen Sie sich I ^ A als Maß dafür vor, wie schwierig es ist, den Körper um Punkt A zu drehen. Stellen Sie sich beispielsweise einen Bleistift (Flachstift) vor. Wenn wir das Trägheitsmoment nahe der Mitte des Stifts messen, erhalten wir einen bestimmten Wert, der der Summe der Quadrate der Abstände entspricht, die entsprechend der Masse jedes Punkts skaliert sind. Wenn wir dagegen die Trägheit an der Spitze desselben Stifts messen, erhalten wir einen größeren Wert, denn je weiter die Punkte mit der Masse entfernt werden, desto größer ist der Wert der Quadrate ihrer Abstände. Hier werden wir mathematisch formulieren, was für uns intuitiv ist: Das Drehen eines Bleistifts um seine Mitte ist viel einfacher (lesen Sie, es erfordert weniger Aufwand) als das Drehen um eines der Enden.

Schließlich sind wir bereit, einen Zusammenhang zwischen den Winkelgleichungen der Dynamik und den Winkelgleichungen der Kinematik herzustellen. Wenn wir Gleichung 13 differenzieren, erhalten wir links das Gesamtkraftmoment und rechts das Produkt aus Trägheitsmoment und Winkelbeschleunigung (I ^ A ist eine Konstante, wir setzen sie außerhalb des Differenzierungszeichens):

$$

$$τ^{AT} = {dL^{AT} \over dt} = {d( I^A ω) \over dt} = I^A ω = I^A α$$

Gleichung 14

Diese Gleichung ist das Winkeläquivalent von Gleichung 5; Tatsächlich ist es F = ma für die Winkeldynamik. Dies ist die Gleichung der Verbindung des Gesamtkraftmoments und der Winkelbeschleunigung des Körpers durch das skalare Trägheitsmoment. Wenn wir das auf unseren Körper ausgeübte Kraftmoment kennen, können wir seine Winkelbeschleunigung und dann die Winkelgeschwindigkeit und Orientierung im Raum durch Integration finden - indem wir das Kraftmoment durch das Trägheitsmoment teilen.

Dynamik-Algorithmus

Er sieht uns kaum durch diesen Wirbelwind von Gleichungen, aber alle sind ihr integraler Bestandteil. Wir haben genug Gleichungen abgeleitet, um die großartige Dynamik einer zweidimensionalen Welt mit willkürlich gegebenen Kräften und Momenten von Kräften zu erhalten, die unsere Objekte bewegen und drehen. Wie verwende ich diese Gleichungen? Unten ist der grundlegende Algorithmus:

1. Finden Sie den Wert des Massenschwerpunkts und das Trägheitsmoment im Massenschwerpunkt.
2. Stellen Sie die Anfangskoordinaten des Körpers, seine Ausrichtung im Raum, seine linearen und Winkelgeschwindigkeiten ein.
3. Berücksichtigen Sie alle auf den Körper einwirkenden Kräfte und die Punkte ihrer Anwendung.
4. Finden Sie das Ergebnis aller Kräfte und dividieren Sie es durch die Masse des Körpers, um die lineare Beschleunigung des Massenschwerpunkts zu ermitteln (Gleichung 5).
5. , , , ( 11).
6. ( 14).
7. , , ( ).
8. , 3.

Im obigen Algorithmus gibt es nur zwei Schritte, die ich nicht erklärt habe. Wie berechnet man zunächst das Trägheitsmoment in Schritt 1 für ein festes Objekt? Zweitens, wie kann das Problem mit den Kräften aus Schritt 3 gelöst werden? Die Antwort auf die erste Frage finden Sie in einem einfachen Codebeispiel, das ich in der Anwendung am Ende dieses Artikels belassen werde (Sie werden das Objekt nach seiner Fläche integrieren). Viele Bücher über Dynamik enthalten das berechnete Trägheitsmoment für häufig vorkommende Formen von Objekten in der Anwendung ganz am Ende, sodass Sie sie nicht jedes Mal selbst anzeigen müssen.

Die Antwort auf die Frage, wie die Kräfte aus Schritt 3 berechnet werden sollen, hängt von der Anwendung ab, aber ich werde einige allgemeine Empfehlungen geben. Erstens erzeugen Kräfte wie die Schwerkraft, die immer in eine Richtung gerichtet sind (im Fall der Schwerkraft nach unten), kein Kraftmoment, da sie alle Punkte gleichzeitig in die gleiche Richtung ziehen, obwohl wir Wir wenden diese Kräfte direkt auf den Schwerpunkt an. Kräfte, die der elastischen Kraft ähnlich sind, werden auf einen bestimmten Punkt des Objekts ausgeübt. Sie erzeugen ein Kraftmoment, daher betrachten wir sie im allgemeinen Fall. Wie wir im ersten Artikel gesehen haben, ist die Reibungskraft dieselbe Kraft, die in die Richtung gerichtet ist, die der Geschwindigkeit des Körpers entgegengesetzt ist.

Sie können ein einfaches physikalisches Modell erstellen, das die Reibungskraft demonstriert, und einfach eine Kraft auf den Schwerpunkt ausüben, oder Sie können auswählen, welche Teile des Objekts Reibungskräfte aufbringen, und dies tun, wodurch ein auf das Objekt einwirkendes Kraftmoment erzeugt wird. Die Kräfte, denen Körper bei Kollisionen ausgesetzt sind, sind etwas schwieriger, und wir werden sie im nächsten Artikel kennenlernen. Kräfte wie der Schub eines Raketentriebwerks sollten als Kräfte mit einem Angriffspunkt betrachtet werden (in diesem Fall, wenn einer der Triebwerke ausfällt, beginnen Sie, sich um seine Achse zu drehen, bis Sie das Lenkrad einstellen, um das Moment der Kraft auszugleichen!). Wenn Sie etwas Ähnliches wie Gravitationsstrahlen von einem UFO wünschen, sollte diese Kraft als Schwerkraft berechnet werden und kein Kraftmoment erzeugen, oder sie sollte auf einen bestimmten Punkt auf dem Objekt angewendet werden.und wird es sich um diesen Punkt drehen, während es aufsteht? Sie haben die Wahl. Der entscheidende Punkt ist, keine Angst zu haben, mit verschiedenen Kräften zu experimentieren, die auf unterschiedliche Weise berechnet wurden, denn jetzt haben Sie einen echten zweidimensionalen Grafiksimulator. Probieren Sie verschiedene Arten von Kräften aus!

Ich habe den gesamten Code und die Links, die Sie benötigen, auf meiner Website hinterlassen, da kein Platz mehr vorhanden ist. In meiner einfachen Anwendung habe ich den Algorithmus der Dynamik einer zweidimensionalen Welt implementiert und Objekte hinzugefügt, die mit einer Feder befestigt sind. Sie drehen sich um ihre Achse und kollidieren manchmal sogar mit Wänden, drehen sich. Aber ich werde ein anderes Mal darüber sprechen. Folgen Sie dem Link für weitere Literatur und eine einfache Anwendung für Windows 32 und Macintosh.

Sehr selten erfährt Chris Hecker den Effekt des Trägheitsmoments, aber normalerweise vergeht er ziemlich schnell. Kräfte können an checker@bix.com angewendet werden.

Anmerkungen des Übersetzers: Hier wird ein Wortspiel vorgestellt, das Thema des Artikels und sein Inhalt werden abgespielt.

PS Feedback ist willkommen. Ihre Kommentare können die Qualität der Arbeit verbessern. Vielen Dank!

PPS Der Autor der Übersetzung bedankt sich ganz besonders bei den Nutzern von berez und Vasily Tereshkov für die Bearbeitung der Übersetzung. Vielen Dank!