Adaptive Antennenarrays: Wie funktioniert es? (Grundlagen)

Guten Tag.

In den letzten Jahren habe ich mich der Erforschung und Entwicklung verschiedener Algorithmen zur räumlichen Verarbeitung von Signalen in adaptiven Antennenarrays gewidmet, und dies mache ich im Rahmen meiner gegenwärtigen Arbeit weiter. Hier möchte ich das Wissen und die Chips teilen, die ich entdeckt habe. Ich hoffe, dass es für Leute nützlich sein wird, die anfangen, diesen Bereich der Signalverarbeitung zu studieren oder nur interessiert sind.

Was ist ein adaptives Antennenarray?

Ein Antennenarray ist ein Satz von Antennenelementen, die auf irgendeine Weise im Raum angeordnet sind. Um die Struktur des adaptiven Antennenarrays zu vereinfachen, die wir betrachten werden, kann sie in der folgenden Form dargestellt werden:


Adaptive Antennenarrays werden häufig als „Smart-Antennen“ ( Smart- Antennen) bezeichnet. Das "intelligente" Antennenarray wird von der räumlichen Signalverarbeitungseinheit und den darin implementierten Algorithmen hergestellt. Diese Algorithmen analysieren das empfangene Signal und bilden eine Reihe von Gewichten$$ $ inline $ w_1 ... w_N $ inline $ die die Amplitude und Anfangsphase des Signals für jedes der Elemente bestimmen. Die gegebene Amplitudenphasenverteilung bestimmt das Richtungsmuster des gesamten Gitters als Ganzes. Die Fähigkeit, das Strahlungsmuster der erforderlichen Form zu synthetisieren und während der Signalverarbeitung zu ändern, ist eines der Hauptmerkmale adaptiver Antennenarrays, mit denen eine Vielzahl von Problemen gelöst werden können . Aber das Wichtigste zuerst.

Wie entsteht das Strahlungsmuster?

Ein Strahlungsmuster charakterisiert die Leistung eines in eine bestimmte Richtung abgestrahlten Signals. Der Einfachheit halber setzen wir die Gitterelemente isotrop, d.h. Für jeden von ihnen hängt die Leistung des ausgesendeten Signals nicht von der Richtung ab. Die Verstärkung oder Dämpfung der von der Anordnung in einer bestimmten Richtung abgestrahlten Leistung wird aufgrund der Interferenz von elektromagnetischen Wellen erhalten, die von verschiedenen Elementen der Antennenanordnung emittiert werden. Ein stabiles Interferenzmuster für EMW ist nur möglich, wenn sie kohärent sind , d.h. Die Phasendifferenz der Signale sollte sich nicht mit der Zeit ändern. Im Idealfall sollte jedes der Elemente des Antennenarrays ein harmonisches Signal mit derselben Trägerfrequenz aussenden$$ $ inline $ f_ {0} $ inline $ . In der Praxis ist es jedoch erforderlich, mit Schmalbandsignalen mit einem Spektrum endlicher Breite zu arbeiten$$ $ inline $ \ Delta f << f_ {0} $ inline $ .
Lassen Sie alle AR- Elemente das gleiche Signal mit komplexer Amplitude aussenden$$ $ inline $ x_n (t) = u (t) $ inline $ . Dann kann am entfernten Empfänger das vom n-ten Element empfangene Signal in einer analytischen Form dargestellt werden:

$$$$ Anzeige $$ a_n (t) = u (t- \ tau_n) e ^ {i2 \ pi f_0 (t- \ tau_n)} $$ Anzeige $$

wo$$ $ inline $ \ tau_n $ inline $ - Verzögerung der Signalausbreitung vom Antennenelement zum Empfangspunkt.
Ein solches Signal ist "quasi-harmonisch", und um die Kohärenzbedingung zu erfüllen, ist es notwendig, dass die maximale Verzögerung bei der Ausbreitung elektromagnetischer Wellen zwischen zwei beliebigen Elementen viel geringer ist als die charakteristische Zeit der Signalhüllkurvenänderung$$ $ inline $ T $ inline $ d.h.$$ $ inline $ u (t- \ tau_n) ≈ u (t- \ tau_m) $ inline $ . Somit kann die Bedingung für die Kohärenz eines Schmalbandsignals wie folgt geschrieben werden:

$$$$ display $$ T≈ \ frac {1} {\ Delta f} >> \ frac {D_ {max}} {c} = max (\ tau_k- \ tau_m) $$ display $$

wo$$ $ inline $ D_ {max} $ inline $ - der maximale Abstand zwischen den Elementen des AR und$$ $ inline $ mit $ inline $ Ist die Lichtgeschwindigkeit.

Beim Empfang eines Signals wird eine kohärente Summierung digital in der räumlichen Verarbeitungseinheit durchgeführt. In diesem Fall wird der komplexe Wert des digitalen Signals am Ausgang dieses Blocks durch den Ausdruck bestimmt:

$$$$ display $$ y = \ sum_ {n = 1} ^ Nw_n ^ * x_n $$ display $$

Es ist bequemer, den letzten Ausdruck in Form eines Skalarprodukts von N-dimensionalen komplexen Vektoren in Matrixform darzustellen:

$$$$ display $$ y = (\ textbf {w}, \ textbf {x}) = \ textbf {w} ^ H \ textbf {x} $$ display $$

wobei w und x Spaltenvektoren sind und$$ $ inline $ (.) ^ H $ inline $ - Operation der hermitianischen Paarung .

Die Vektordarstellung von Signalen ist eine der Grundlagen bei der Arbeit mit Antennenarrays, weil vermeidet oft umständliche mathematische Berechnungen. Darüber hinaus ermöglicht die Identifizierung eines zu einem bestimmten Zeitpunkt empfangenen Signals mit einem Vektor häufig die Abstraktion von einem realen physikalischen System und das Verständnis dessen, was unter dem Gesichtspunkt der Geometrie genau geschieht.

Um das Richtcharakteristikmuster des Antennenarrays zu berechnen, ist es notwendig, mental und konsistent einen Satz ebener Wellen aus allen möglichen Richtungen darauf zu "laufen". In diesem Fall können die Werte der Elemente des Vektors x wie folgt dargestellt werden:

$$$$ display $$ x_n = s_n = \ exp \ {- i (\ textbf {k} (\ phi, \ theta), \ textbf {r} _n) \} $$ display $$

wobei k der Wellenvektor ist$$ $ inline $ \ phi $ inline $ und$$ $ inline $ \ theta $ inline $ - Azimutwinkel und Elevationswinkel, der die Ankunftsrichtung einer ebenen Welle kennzeichnet,$$ $ inline $ \ textbf {r} _n $ inline $ - Koordinate des Antennenelements,$$ $ inline $ s_n $ inline $ - ein Element des Phasenvektors s einer ebenen Welle mit dem Wellenvektor k (in der englischen Literatur wird der Phasenvektor als Steuervektor bezeichnet). Die Abhängigkeit des Quadrats von der Amplitude von y von$$ $ inline $ \ phi $ inline $ und$$ $ inline $ \ theta $ inline $ bestimmt das Richtungsmuster des Antennenarrays beim Empfang für einen gegebenen Vektor von Gewichtskoeffizienten w .

Merkmale des Antennenarrays

Es ist zweckmäßig, die allgemeinen Eigenschaften des Antennenarray-Strahlungsmusters auf einem linearen äquidistanten Antennenarray in einer horizontalen Ebene zu untersuchen (d. H. Das Strahlmuster hängt nur vom Azimutwinkel ab$$ $ inline $ \ phi $ inline $ ) Dies ist unter zwei Gesichtspunkten praktisch: analytische Berechnungen und visuelle Darstellung.

Wir berechnen den DN für einen Einheitsgewichtsvektor ($$ $ inline $ w_n = 1, n = 1 ... N $ inline $ ) nach dem oben beschriebenen Ansatz.


Als Ergebnis erhalten wir:

$$$$ display $$ F (\ phi) = | y | ^ 2 = \ frac {\ sin ^ 2 (\ pi \ frac {Nd} {\ lambda} \ sin \ phi)} {\ sin ^ 2 (\ pi \ frac {d} {\ lambda} \ sin \ phi)} $$ display $$

Strahlungsmusterfrequenz

Das resultierende Strahlungsmuster des Antennenarrays ist eine periodische Funktion des Sinus des Winkels. Dies bedeutet, dass für bestimmte Werte des d / λ- Verhältnisses Beugungsmaxima (zusätzliche Maxima) vorliegen.
Nicht normalisiertes Antennenmuster für N = 5
Normalisiertes Strahlungsmuster des Antennenarrays für N = 5 im Polarkoordinatensystem

Die Position der "Beuger" kann direkt aus der Formel für NAM entnommen werden. Wir werden jedoch versuchen zu verstehen, woher sie physikalisch und geometrisch kommen (im N-dimensionalen Raum).

Die Elemente des Phasenvektors sind komplexe Exponenten$$ $ inline $ e ^ {i \ Psi n} $ inline $ deren Werte werden durch den Wert des verallgemeinerten Winkels bestimmt$$ $ inline $ \ Psi = 2 \ pi \ frac {d} {\ lambda} \ sin \ phi $ inline $ . Wenn es zwei verallgemeinerte Winkel gibt, die unterschiedlichen Ankunftsrichtungen einer ebenen Welle entsprechen, für die$$ $ inline $ \ Psi_1 = \ Psi_2 + 2 \ pi m $ inline $ dann bedeutet dies zwei Dinge:

• Physikalisch: ebene Wellenfronten, die aus diesen Richtungen kommen, induzieren identische Amplituden-Phasen-Verteilungen elektromagnetischer Wellen auf den Elementen des Antennenarrays.
• Geometrisch: Phasenvektoren für diese beiden Richtungen fallen zusammen.

Die auf ähnliche Weise verbundenen Richtungen der Wellenankunft sind aus Sicht des Antennenarrays äquivalent und nicht voneinander unterscheidbar.

Wie kann man den Winkelbereich bestimmen, in dem immer nur ein Hauptmaximum der MD liegt? Wir werden dies aus folgenden Gründen in der Nähe des Null-Azimuts tun: Die Phasenverschiebung zwischen zwei benachbarten Elementen sollte im Intervall von liegen$$ $ inline $ - \ pi $ inline $ vorher$$ $ inline $ \ pi $ inline $ .

$$$$ display $$ - \ pi <2 \ pi \ frac {d} {\ lambda} \ sin \ phi <\ pi $$ display $$

Wenn wir diese Ungleichung lösen, erhalten wir die Bedingung für den Bereich der Einzigartigkeit in einer Nachbarschaft von Null:

$$$$ display $$ | \ sin \ phi | <\ frac {\ lambda} {2d} $$ display $$

Es ist ersichtlich, dass die Größe des Bereichs der Eindeutigkeit im Winkel vom Verhältnis d / λ abhängt. Wenn d = 0,5 λ ist , ist jede Ankunftsrichtung des Signals "individuell", und der Bereich der Eindeutigkeit deckt den gesamten Winkelbereich ab. Wenn d = 2,0 λ ist , sind die Richtungen 0, ± 30, ± 90 äquivalent. Beugungskeulen erscheinen auf dem Strahlungsmuster.

Typischerweise neigen Beugungskeulen dazu, unter Verwendung von Richtantennenelementen zu unterdrücken. In diesem Fall ist das vollständige Strahlungsmuster des Antennenarrays das Produkt des Musters eines Elements und des Arrays isotroper Elemente. Die DN- Parameter eines Elements werden normalerweise basierend auf der Bedingung des Eindeutigkeitsbereichs des Antennenarrays ausgewählt.

Die Breite des Hauptlappens

Die technische Formel zum Schätzen der Breite der Hauptkeule des Antennensystems ist allgemein bekannt :$$ $ inline $ \ Delta \ phi ≈ \ frac {\ lambda} {D} $ inline $ Dabei ist D die charakteristische Größe der Antenne. Die Formel wird für verschiedene Antennentypen verwendet, einschließlich SLR-Antennen. Wir zeigen, dass es auch für Antennenarrays gilt.

Wir bestimmen die Breite der Hauptkeule durch die ersten Nullen der MD in der Nähe des Hauptmaximums. Zähler des Ausdrucks für$$ $ inline $ F (\ phi) $ inline $ verschwindet bei$$ $ inline $ \ sin \ phi = m \ frac {\ lambda} {dN} $ inline $ . Die ersten Nullen entsprechen m = ± 1. Vorausgesetzt$$ $ inline $ \ frac {\ lambda} {dN} << 1 $ inline $ wir bekommen$$ $ inline $ \ Delta \ phi = 2 \ frac {\ lambda} {dN} $ inline $ .

Typischerweise wird die Richtstrahlbreite AR durch den halben Leistungspegel (-3 dB) bestimmt. Verwenden Sie in diesem Fall den Ausdruck:

$$$$ display $$ \ Delta \ phi≈0.88 \ frac {\ lambda} {dN} $$ display $$

Die Breite der Hauptkeule kann gesteuert werden, indem unterschiedliche Werte der Amplituden für die Gewichtskoeffizienten des Antennenarrays eingestellt werden. Betrachten Sie drei Verteilungen:

• Gleichmäßige Amplitudenverteilung (Gewichte 1):$$ $ inline $ w_n = 1 $ inline $ .
• Amplitudenwerte, die an die Gitterkanten fallen (Gewichte 2):$$ $ inline $ w_n = 0,5 + 0,3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ inline $
• Amplitudenwerte, die bis zu den Rändern des Gitters ansteigen (Gewichte 3):$$ $ inline $ w_n = 0,5-0,3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ inline $

Die Abbildung zeigt die resultierenden normalisierten Strahlungsmuster auf einer logarithmischen Skala:
Die folgenden Tendenzen können aus der Figur beobachtet werden: Die Verteilung der Amplituden der Gewichtskoeffizienten, die zu den Rändern des Gitters hin abnimmt, führt zu einer Verbreiterung des Hauptlappens des MD, jedoch zu einer Abnahme des Niveaus der Nebenkeulen. Die zu den Rändern der Antennenanordnung hin zunehmenden Amplituden führen im Gegensatz dazu zu einer Verengung der Hauptkeule und einer Erhöhung des Niveaus der Seiten. Es ist zweckmäßig, hier Grenzfälle zu berücksichtigen:

1. Die Amplituden der Gewichtungskoeffizienten aller Elemente mit Ausnahme der extremen sind gleich Null. Gewichte für extreme Elemente sind gleich Einheit. In diesem Fall wird das Gitter äquivalent zu einem Zwei-Elemente-AR mit einer Periode von D = (N-1) d . Es ist nicht schwierig, die Breite des Hauptblatts gemäß der obigen Formel abzuschätzen. In diesem Fall verwandeln sich die Seitenteile in Beugungsmaxima und richten sich nach dem Hauptmaximum aus.
2. Das Gewicht des zentralen Elements ist gleich Eins und der Rest gleich Null. In diesem Fall haben wir im Wesentlichen eine Antenne mit einem isotropen Strahlungsmuster.

Die Richtung des Hauptmaximums

Wir haben uns also angesehen, wie Sie die Breite der Hauptkeule des AP AR anpassen können. Nun wollen wir sehen, wie man die Richtung steuert. Rufen Sie den Vektorausdruck für das empfangene Signal auf. Angenommen, wir möchten, dass das maximale Strahlungsmuster in eine bestimmte Richtung zeigt$$ $ inline $ \ phi_0 $ inline $ . Dies bedeutet, dass die maximale Leistung aus dieser Richtung entnommen werden sollte. Der Phasenvektor entspricht dieser Richtung$$ $ inline $ \ textbf {s} (\ phi_0) $ inline $ im N- dimensionalen Vektorraum, und die Empfangsleistung ist definiert als das Quadrat des Skalarprodukts dieses Phasenvektors durch den Vektor der Gewichtskoeffizienten w . Das Skalarprodukt zweier Vektoren ist maximal, wenn sie kollinear sind , d.h.$$ $ inline $ \ textbf {w} = \ beta \ textbf {s} (\ phi_0) $ inline $ wobei β ein normalisierender Faktor ist. Wenn wir also einen Gewichtsvektor wählen, der dem Phasenvektor für die gewünschte Richtung entspricht, drehen wir das maximale Strahlungsmuster.

Betrachten Sie die folgenden Gewichte als Beispiel:$$ $ inline $ \ textbf {w} = \ textbf {s} (10 °) $ inline $

$$$$ display $$ w_n = \ exp \ {i2 \ pi \ frac {d} {\ lambda} (n-1) \ sin (10 \ pi / 180) \} $$ display $$

Als Ergebnis erhalten wir ein Strahlungsmuster mit dem Hauptmaximum in Richtung 10 °.

Jetzt wenden wir die gleichen Gewichte an, jedoch nicht für den Signalempfang, sondern für die Übertragung. Hierbei ist zu berücksichtigen, dass bei der Übertragung eines Signals die Richtung des Wellenvektors umgekehrt wird. Dies bedeutet, dass sich die Elemente des Phasenvektors zum Empfangen und Senden im Exponenten im Vorzeichen unterscheiden, d.h. durch komplexe Konjugation miteinander verbunden. Als Ergebnis erhalten wir das Maximum des Strahlungsmusters in Richtung von -10 °, das nicht mit dem Maximum des Empfangssignals bei gleichen Gewichtskoeffizienten übereinstimmt. Um die Situation zu korrigieren, ist es notwendig, eine komplexe Konjugation auch auf die Gewichtskoeffizienten anzuwenden.

Das beschriebene Merkmal der Bildung der Strahlen zum Empfangen und Senden sollte bei der Arbeit mit Antennenarrays immer berücksichtigt werden.

Spielen wir mit dem Strahlungsmuster

Nur wenige Höhen

Wir stellen das Problem, zwei Hauptmaxima des Strahlungsmusters in der Richtung zu bilden: -5 ° und 10 °. Dazu wählen wir die gewichtete Summe der Phasenvektoren für die entsprechenden Richtungen als Gewichtsvektor.

$$$$ display $$ \ textbf {w} = \ beta \ textbf {s} (10 °) + (1- \ beta) \ textbf {s} (- 5 °) $$ display $$

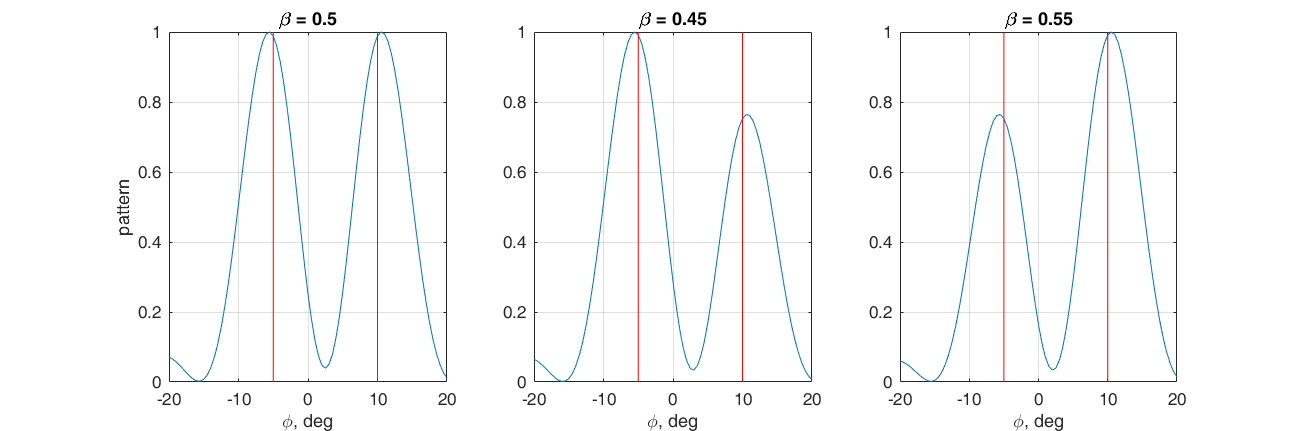
Durch Einstellen des Koeffizienten β kann das Verhältnis zwischen den Hauptkeulen eingestellt werden. Auch hier ist es bequem zu sehen, was im Vektorraum passiert. Wenn β größer als 0,5 ist, liegt der Gewichtsvektor näher an s (10 °), andernfalls an s (-5 °). Je näher der Gewichtsvektor an einem der Zeiger liegt, desto größer ist das entsprechende Skalarprodukt und damit die Größe des entsprechenden Maximums der ND .

Es ist jedoch zu bedenken, dass beide Hauptblütenblätter eine endliche Breite haben. Wenn wir in zwei nahe Richtungen stimmen möchten, verschmelzen diese Blütenblätter zu einer, die auf eine mittlere Richtung ausgerichtet ist.

Ein Maximum und Null

Versuchen wir nun, das maximale Strahlungsmuster an die Richtung anzupassen$$ $ inline $ \ phi_1 = 10 ° $ inline $ und gleichzeitig das aus der Richtung kommende Signal unterdrücken$$ $ inline $ \ phi_2 = -5 ° $ inline $ . Dazu muss für den entsprechenden Winkel die Null gesetzt werden. Sie können dies wie folgt tun:

$$$$ display $$ \ textbf {w} = \ textbf {s} _1- \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {N} \ textbf {s} _2 $$ display $$

wo$$ $ inline $ \ textbf {s} _1 = \ textbf {s} (10 °) $ inline $ und$$ $ inline $ \ textbf {s} _2 = \ textbf {s} (- 5 °) $ inline $ .

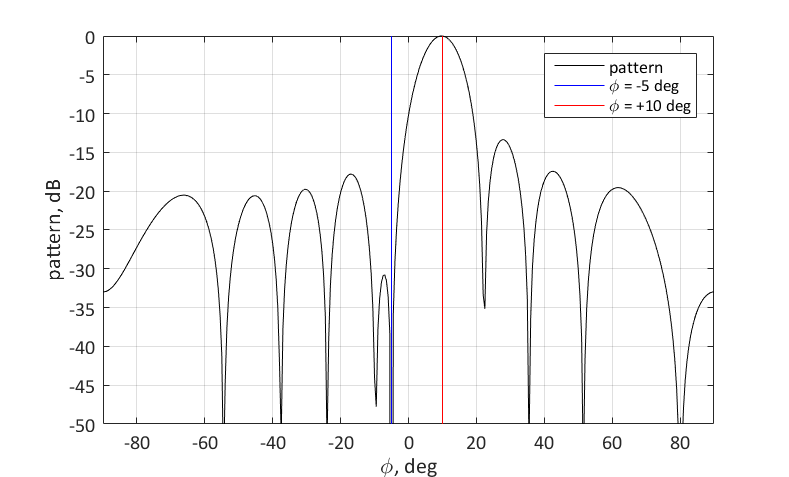
Die geometrische Bedeutung der Wahl des Gewichtsvektors ist wie folgt. Wir wollen, dass dieser Vektor w eine maximale Projektion hat$$ $ inline $ \ textbf {s} _1 $ inline $ und war orthogonal zum Vektor$$ $ inline $ \ textbf {s} _2 $ inline $ . Vektor$$ $ inline $ \ textbf {s} _1 $ inline $ kann als zwei Begriffe dargestellt werden: kollinearer Vektor$$ $ inline $ \ textbf {s} _2 $ inline $ und orthogonaler Vektor$$ $ inline $ \ textbf {s} _2 $ inline $ . Um die Problemstellung zu erfüllen, muss die zweite Komponente als Vektor der Gewichtskoeffizienten w gewählt werden . Die kollineare Komponente kann durch Entwerfen eines Vektors berechnet werden$$ $ inline $ \ textbf {s} _1 $ inline $ zum normalisierten Vektor$$ $ inline $ \ frac {\ textbf {s} _2} {\ sqrt {N}} $ inline $ mit einem skalaren Produkt.

$$$$ display $$ \ textbf {s} _ {1 ||} = \ frac {\ textbf {s} _2} {\ sqrt {N}} \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {\ sqrt {N}} $$ display $$

Dementsprechend wird vom anfänglichen Phasenvektor subtrahiert$$ $ inline $ \ textbf {s} _1 $ inline $ Mit seiner kollinearen Komponente erhalten wir den gewünschten Gewichtsvektor.

Einige zusätzliche Hinweise

1. Überall oben habe ich die Frage der Normalisierung des Gewichtsvektors weggelassen, d.h. seine Länge. Die Normalisierung des Gewichtsvektors beeinflusst also nicht die Eigenschaften des Antennenarray-Strahlungsmusters: die Richtung der Hauptmaxime, die Breite der Hauptkeule usw. Es kann auch gezeigt werden, dass diese Normalisierung das SNR am Ausgang des räumlichen Verarbeitungsblocks nicht beeinflusst. In dieser Hinsicht akzeptiere ich, wenn räumliche Signalverarbeitungsalgorithmen betrachtet werden, normalerweise eine Einheitsnormalisierung des Gewichtsvektors, d.h.$$ $ inline $ \ textbf {w} ^ H \ textbf {w} = 1 $ inline $
2. Die Möglichkeiten zur Bildung des Antennenarraybodens werden durch die Anzahl der Elemente N bestimmt. Je mehr Elemente, desto breiter die Möglichkeiten. Je mehr Freiheitsgrade bei der Implementierung der räumlichen Gewichtsverarbeitung vorhanden sind, desto mehr Optionen zum "Verdrehen" des Gewichtsvektors im N-dimensionalen Raum.
3. Beim Empfang des Antennenstrahlmusters existiert das Antennenarray physikalisch nicht, und all dies existiert nur in der "Vorstellung" der Recheneinheit, die das Signal verarbeitet. Dies bedeutet, dass es gleichzeitig möglich ist, mehrere MDs zu synthetisieren und unabhängig voneinander Signale zu verarbeiten, die aus verschiedenen Richtungen ankommen. Bei der Übertragung ist alles etwas komplizierter, es ist aber auch möglich, mehrere MDs zur Übertragung verschiedener Datenströme zu synthetisieren. Diese Technologie in Kommunikationssystemen heißt MIMO .
4. Mit dem bereitgestellten Matlab-Code können Sie selbst mit NAM spielen
   
   Code

   % antenna array settings N = 10; % number of elements d = 0.5; % period of antenna array wLength = 1; % wavelength mode = 'receiver'; % receiver or transmitter % weights of antenna array w = ones(N,1); % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).'; % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % w = s1 - (1/N)*s2*s2'*s1; % w = s1; % normalize weights w = w./sqrt(sum(abs(w).^2)); % set of angle values to calculate pattern angGrid_deg = (-90:0.5:90); % convert degree to radian angGrid = angGrid_deg * pi / 180; % calculate set of steerage vectors for angle grid switch (mode) case 'receiver' s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); case 'transmitter' s = exp(-2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); end % calculate pattern y = (abs(w'*s)).^2; %linear scale plot(angGrid_deg,y/max(y)); grid on; xlim([-90 90]); % log scale % plot(angGrid_deg,10*log10(y/max(y))); % grid on; % xlim([-90 90]); 

   
   

Welche Aufgaben können mit Hilfe eines adaptiven Antennenarrays gelöst werden?

Vielen Dank für Ihre Aufmerksamkeit