Dies ist eine Übersetzung eines Artikels von Eliezer Yudkovsky aus einem populärwissenschaftlichen Zyklus, der sich der multivariaten Interpretation der Quantenmechanik widmet. Der Beginn des Zyklus wurde in einen Hub übersetzt , aber dann wurde der Übersetzer anscheinend müde. Es kann verstanden werden - das Material ist sehr voluminös. Yudkovsky liebt es, Gedanken auf dem Baum zu verbreiten. Andererseits ist das Material wirklich komplex, und die Wiederholung derselben Sache in verschiedenen Worten ermöglicht es dem Bild im Kopf eines unvorbereiteten Lesers, zumindest irgendwie in sich zu bleiben. Ich werde mich nicht verpflichten, die Übersetzung des gesamten Zyklus fortzusetzen, aber ich werde versuchen, einige der wichtigsten Artikel zu übersetzen.

Ich werde Artikel in der Reihe über Zustandsräume ( klassisch und quantenmäßig ) überspringen - das Konzept wird häufig dort verwendet und sollte einem technisch geschulten Leser vertraut sein. Überspringen Sie auch die Feynman-Pfadintegrale - sie finden Sie in der hervorragenden populärwissenschaftlichen Quelle .

Aber der nächste Beitrag beantwortet eine wichtige Frage. Wenn die „reale“ Welt auf der fundamentalen Ebene Quanten ist, wo alles verwirrt ist und sich alles gegenseitig beeinflusst, woher kommen klassische Systeme? Warum sehen wir im normalen Leben so selten „natürliche“ Quantenphänomene? Dies nennt der Autor "klassische Halluzination". Warum müssen beispielsweise Entwickler von Quantencomputern so enorme Anstrengungen unternehmen, um das System in einem "natürlichen" Zustand zu halten?

Haftungsausschluss: Ich bin weder ein professioneller Physiker noch ein professioneller Übersetzer (sowie der Autor des Originals).

Dekohärenz

Um einen Quantenprozess namens „Dekohärenz“ zu verstehen, müssen Sie zunächst verstehen, wie ein spezieller Zustand der Quantenunabhängigkeit zerstört wird - das heißt, wie genau ein Quantensystem von einem Zustand der Unabhängigkeit in einen Zustand der Verschränkung übergeht.

Wie wir uns erinnern , ist die Quantenunabhängigkeit ein spezieller, „rechteckiger“ Zustand der Amplitudenverteilung, der gut faktorisiert ist. Das heißt, es kann als Produkt der Verteilungen der Bestandteile des Systems dargestellt werden, die für uns wie „separate Partikel“ aussehen.

Schüchterne Touristen, die unsere Quantenwelt besuchen, nehmen manchmal das Fehlen einer solchen „rechteckigen“ Verteilung für eine besondere mysteriöse Verbindung zwischen Teilchen. Daher der unglückliche Begriff "Quantenverschränkung". Tatsächlich erzeugt jede Entwicklung eines Quantensystems normalerweise eine Verschränkung von der Unabhängigkeit (und nicht umgekehrt), wodurch rechteckige Verteilungen in nicht rechteckige umgewandelt werden. Unabhängigkeit ist selten und sehr leicht zu zerstören.

Um genau zu verstehen, welche physikalischen Prozesse zur Verschränkung führen, beginnen wir mit dem klassischen System. Die Figur zeigt ein System eines positiv geladenen leichten Balls auf der oberen Spur und eines negativ geladenen schweren Balls auf der unteren Spur. Anfangs sind zwei Bälle weit voneinander entfernt und interagieren fast nicht. Dann senken wir den oberen Pfad und bringen die Kugeln zusammen, so dass sie sich gegenseitig anziehen (entgegengesetzte Ladungen werden angezogen). Und ein leichter Ball rollt zu einem schweren (und ein schwerer Ball rollt ein wenig zu einem leichten, so wie ein fallender Apfel die Erde leicht zu sich zieht).

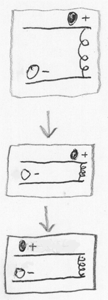
Betrachten wir dieses System nun als ein Quantensystem aus der Sicht der Feynman-Pfadintegrale . Das heißt, wir repräsentieren die Entwicklung des Systems als die Summe aller möglichen Trajektorien vom Anfangszustand im Konfigurationsraum. Angenommen, zwei Kugeln sind anfangs quantenunabhängig, und ihre gemeinsame Amplitudenverteilung kann als Produkt aus „Verteilung für die untere Kugel“ und „Verteilung für die obere Kugel“ dargestellt werden.

Ferner sei die Amplitude der unteren Kugel zu Beginn aus drei Teilen (die aus Sicht der Feynman-Integrale als drei Anfangszustände betrachtet werden können). Wenn wir die obere Spur absenken, sollte die obere Kugel zur unteren gezogen werden. Wenn die Gelenkamplitude der unteren Kugel jedoch aus mehreren Teilen besteht, erhalten wir am Ende eine Gelenkverteilung , die aus mehreren Teilen besteht, von denen jedes die neue Position der Kugeln beschreibt.

Ich gebe mein Bestes, um Formulierungen wie „Der untere Ball kann sich an einer von drei Stellen befinden“ oder „In jedem Fall wird der obere Ball von der entsprechenden Position des unteren Balls angezogen“ zu vermeiden. Obwohl Sie sich wahrscheinlich immer noch alles so vorstellen. Am Ende habe ich das selbst illustriert. Ich habe drei mögliche Startpositionen und drei mögliche Ergebnisse gezogen. Was zu tun ist, stellt sich das menschliche Gehirn normalerweise Feynman-Integrale vor. Dies bedeutet jedoch nicht, dass es drei mögliche Zustände des Universums gibt . Dies ist nur ein Trick zur Visualisierung des Pfadintegrals. Alle drei Komponenten der Amplitude existieren in unserem Universum, alle drei sind gleich real , aber überhaupt nicht möglich oder wahrscheinlich .

Stellen Sie sich nun vor, dass die Amplitude des unteren Balls zunächst über die gesamte Spur „verschmiert“ wird. Die Amplitude der oberen Kugel ist immer noch an einer Stelle konzentriert. Dann hat die Fugenverteilung zunächst die Form eines länglichen Rechtecks ​​und wird dann diagonal.

Auf der X-Achse befindet sich hier die Position der oberen Kugel, auf der Y-Achse die untere. Wir beginnen mit einer genau lokalisierten oberen Kugel und einer „verschwommenen“ unteren Kugel und enden mit einer voneinander abhängigen Verteilung, wenn beide Koordinaten verschwommen, aber gleich sind (vereinfacht). Das heißt, die anfänglich faktorisierbare Verteilung wurde zu einem "verwirrenden System" - sie zerfällt nicht mehr in zwei unabhängige Faktoren.

(Wichtiger Hinweis:

Beachten Sie, dass in der obigen Abbildung die Entwicklung des Systems dem zweiten Hauptsatz der Thermodynamik folgt, dem Satz von Liouville. Wenn sich das System ändert, bleibt die „Wolkengröße“ erhalten, dh das Gesamtvolumen der Amplitude oder einfacher die Größe des grauen Bereichs im Diagramm . Wenn zu Beginn der Abbildung ein riesiges hellgraues Quadrat vorhanden war (wenn beide Teilchen im Raum stark verschmiert sind), konnte es nach dem zweiten Hauptsatz der Thermodynamik nicht zu einer dunkelgrauen Diagonale werden. Um in einen Verschränkungszustand zu gelangen, sollte das System zunächst eine niedrige Entropie aufweisen, und diese Entropie sollte dabei nicht stark zunehmen.

Ich möchte Sie daran erinnern, dass gegenseitige Information Entropie mit dem entgegengesetzten Vorzeichen ist . Quantenamplituden sind nicht nur Informationen , aber das Prinzip ist dasselbe. Die anfängliche Amplitude sollte so konzentriert sein, dass anstelle einer großen verdünnten Wolke eine kompakte diagonale Linie entsteht. Wenn wir uns vorstellen, dass die Amplitudenverteilung eine „Quantenentropie“ aufweist, sollte die Entropie des verschränkten Systems relativ niedrig sein.

Schließlich sind wir bereit, über Dekohärenz zu sprechen.

Das System in der Abbildung ist ziemlich kompliziert. Es kann ungefähr so ​​beschrieben werden: "Es gibt zwei Teilchen, und beide können entweder hier oder da sein ." Ja, ich habe es so formuliert, als gäbe es zwei mögliche Zustände und keine physikalisch reale Verteilung der Amplitude. Im Ernst, ich weiß nicht, wie ich die Quantenphysik in einer gewöhnlichen Sprache auf normale Weise beschreiben soll! Denken Sie nur an die allgemeine Regel, dass "Gelegenheit" oder "Wahrscheinlichkeit" eine Abkürzung für "physikalisch vorhandene Strecke der Amplitudenverteilung" ist. Dann kann ich die Amplituden mit den Begriffen der Unsicherheiten viel kürzer beschreiben. Aber denken Sie daran, dass dies nur eine Konvention ist ! "Ein Teilchen ist entweder hier oder da" bedeutet "eine physikalisch existierende Verteilung der Amplitude zweier Teile, eines hier, eines dort" und nicht "das Teilchen befindet sich an einer von zwei Stellen, aber wir wissen nicht, welche".

Also. Die Arbeit mit komplizierten Systemen ist normalerweise schwierig (für Physiker natürlich nicht für das Universum). Zunächst müssen wir alle möglichen Trajektorien für alle möglichen Anfangsbedingungen berechnen (dh alle physikalisch vorhandenen Amplituden-Trajektorien im Feynman-Integral berücksichtigen). Ferner ist es notwendig, den Einfluss dieser Trajektorien aufeinander zu berücksichtigen ( wahrscheinliche Trajektorien im engeren Sinne können nicht interagieren - nur etwas, das wirklich existiert, kann etwas anderes beeinflussen). Zum Beispiel treffen unsere beiden Partikel auf weitere 20 andere, interagieren auf irgendeine Weise und als Ergebnis erhalten wir eine Reihe von Konfigurationen, die von allen vorherigen Punkten aller möglichen Zustände beeinflusst wurden.

Beachten Sie, dass eine Verschränkung nur auftritt, wenn Abschnitte der Anfangsamplitude nahe beieinander liegen. Damit sich ihre Entwicklungspfade kreuzen können. Wenn zwei Teilchen entweder hier oder da sind , aber „hier“ und „dort“ durch einen Abstand von zwei Lichtjahren voneinander getrennt sind, können sich ihre weiteren Flugbahnen frühestens ein Jahr später schneiden.

Fügen Sie nun das dritte Teilchen hinzu. Die Abbildung zeigt einen dreidimensionalen Konfigurationsraum, der sich in unabhängige zweidimensionale und eindimensionale Teilräume zerlegt. Das heißt, zwei verwickelte Teilchen und eines davon unabhängig.

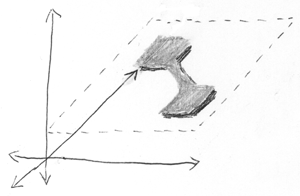
Höhe ist das dritte Teilchen, Breite und Tiefe sind zwei verschränkte Teilchen.

Ein unabhängiges Teilchen befindet sich an einem bestimmten Ort - die vertikale Verteilung ist sehr eng. Zwei verschränkte Teilchen sind entweder hier oder da (ich verwende wieder falsche probabilistische Begriffe wie "spezifisch" und "entweder", aber Sie verstehen, was ich meine).

Stellen Sie sich jetzt vor, dass das dritte Teilchen mit den verwickelten zwei auf eine Weise reagiert, die für ihre Position empfindlich ist. Zum Beispiel gleicht sich das dritte Teilchen auf einem scharfen Peak aus, zwei Teilchen fliegen vorbei, ziehen es an und es fällt entweder in die eine oder andere Richtung. Danach sieht die Amplitude ungefähr so ​​aus.

Das dritte Teilchen wird nun mit den beiden anderen verwechselt. Und die Amplitude besteht jetzt aus zwei voneinander getrennten Teilen. Vereinfachte Beschreibung: „Wenn zwei Partikel hier wären, wäre das dritte Partikel hierher geflogen. Und wenn sie dort wären, wäre sie dorthin geflogen. “ Das heißt, die Amplitude ist völlig verwirrt. Es zerfällt nicht mehr in unabhängige Teilräume.

Aber zwei Amplitudenstücke sind jetzt weiter voneinander entfernt und bestehen jeweils aus drei Teilchen in der entsprechenden Region. Dies geschah, weil das dritte Teilchen für die Koordinate anderer empfindlich ist. Nach dem Rollen von einer scharfen Spitze zu einer von zwei Seiten ist der Abstand zwischen den Endkoordinaten ziemlich groß.

Tatsächlich ist das Herunterrollen von oben optional. Alles funktioniert auf die gleiche Weise, wenn Sie zwanzig Partikel haben, die auf die ersten beiden reagieren und mit ihnen verwechselt werden. Die endgültige Verteilung im 22-dimensionalen Raum sieht aus wie zwei Bereiche, von denen jeder 22 Partikeln entspricht. Und der Abstand zwischen diesen Gebieten wird enorm sein. Und je größer die Entfernung, desto weniger wahrscheinlich ist es, dass sich Gebiete in Zukunft gegenseitig beeinflussen.
Das ist Dekohärenz. Es ist die dritte Ursache für die „klassische Halluzination“, da sich die beiden Bereiche unabhängig voneinander zu entwickeln beginnen. Dadurch können sie als nicht komplizierte Systeme beschrieben werden. Sobald wir sie separat betrachten, sieht die Verteilung in jedem von ihnen "rechteckig" und unabhängig in drei Koordinaten aus (ich habe versucht, dies in der obigen Abbildung zu zeigen).

In einem Quantencomputer ist es sehr schwierig, Dekohärenz zu verhindern . Quantum Computing erfordert, dass die Amplitudenabschnitte nahe beieinander bleiben und interagieren können. Aber es gibt Billionen anderer Teilchen, die ständig versuchen, versehentlich mit unseren zerbrechlichen Qubits zu reagieren und eine genau konstruierte Amplitude zu zerstören.

Und Sie können die zerstörten nicht einfach nehmen und wiederherstellen. Dazu müssen alle umgesetzten Partikel, einschließlich zufälliger Partikel aus der Umgebung, an den Ort zurückkehren (vergessen Sie nicht, dass die endgültige Amplitude eine gemeinsame Verteilung mit ihnen aufweist).

(Es sieht nach einem fast irreversiblen Prozess aus, oder? Es ist, als würde man versuchen, ein zerbrochenes Ei wieder in der Schale zu sammeln. Tatsächlich ist dies eine gute Analogie.

Deshalb habe ich vorhin betont, dass der Verschränkungsprozess mit einer geringen Entropie beginnt. Dekohärenz ist irreversibel, da es sich im Wesentlichen um einen thermodynamischen Prozess handelt.

Eines der grundlegenden physikalischen Prinzipien besagt, dass Sie den Film "zurückrollen" können, ohne gegen grundlegende Gesetze zu verstoßen. Wenn Sie ein Ei filmen, das auf den Boden fällt, und es dann rückwärts rollen, so dass das zerbrochene Ei vom Boden auffliegt und sich wieder zu einer glatten Schale zusammenzieht, werden Sie feststellen, dass kein physikalisches Gesetz verletzt wird. Alle Moleküle werden einfach zur richtigen Zeit am richtigen Ort sein und das Ei wird sicher und gesund vom Boden abprallen. Dies ist nicht unmöglich, nur äußerst unwahrscheinlich.

Gleiches gilt für die in entfernte Teile zerbrochene Amplitude, die unerwartet in einen kohärenten Zustand zurückkehrt - dies ist theoretisch möglich. Es besteht jedoch praktisch keine Chance, dass die ursprünglich getrennten Teile plötzlich gleichzeitig nebeneinander liegen. Der umgekehrte Prozess ist viel wahrscheinlicher.

Zusätzlich zum Zurückrollen des Films müssen Sie auch die Ladungen aller Partikel umkehren sowie die linke und rechte (oder eine der beiden anderen Dimensionen) vertauschen, um das Universum in ein Spiegelbild davon zu verwandeln. Diese Regel wird als "CPT-Invarianz" aus den Wörtern "Ladung", "Parität" und "Zeit" bezeichnet.

Höchstwahrscheinlich ist die CPT-Invarianz eines der grundlegendsten Prinzipien für die Funktionsweise des Universums. Für Physiker sehen Versuche, sie zu brechen, fast so absurd aus wie der Versuch, einen Ball schneller als mit Lichtgeschwindigkeit zu werfen. Soweit ich weiß, ist eine CPT-Invarianz für die Konsistenz der Quantenfeldtheorie erforderlich.

Daher sieht Dekohärenz nur wie ein unidirektionaler Prozess aus, aber tatsächlich ist ihre Irreversibilität thermodynamisch und nicht grundlegend. Und das ist sehr wichtig, denn daraus folgt, dass die Quantenphysik die CPT-Invarianz beobachtet.

Soweit wir wissen, sind absolut alle unidirektionalen Prozesse in der Natur eine Folge des zweiten Hauptsatzes der Thermodynamik und nicht der fundamentalen Asymmetrie der Zeit.)

Zusammenfassend. Dekohärenz ist ein thermodynamischer Prozess einer immer größer werdenden Quantenverschränkung, der überraschenderweise als Prozess der Zerstörung dieser Verschränkung selbst getarnt ist. Dekohärente Bereiche interagieren nicht miteinander und jeder von ihnen wird weniger verwirrend . Dekohärenz ist der dritte Grund für "klassische Halluzination". Es ermöglicht Physikern, jedes Feld als unabhängig zu betrachten, ohne die geringe Wahrscheinlichkeit ihrer Interaktion zu berücksichtigen. Darüber hinaus wird jeder einzelne Bereich innerhalb leichter verständlich. Dies ist sehr nützlich, wenn Sie Probleme in Bezug auf die einfache klassische Physik lösen möchten. Und es ist sehr unangemessen, wenn Sie eine millionenstellige Zahl faktorisieren möchten, bevor die Sonne untergeht.