Den FFT-Algorithmus verstehen

Hallo Freunde. Der Kurs " Algorithmen für Entwickler" beginnt morgen und wir haben noch eine unveröffentlichte Übersetzung. Eigentlich korrigieren wir und teilen Material mit Ihnen. Lass uns gehen.

Die schnelle Fourier-Transformation (FFT) ist einer der wichtigsten Signalverarbeitungs- und Datenanalysealgorithmen. Ich habe es jahrelang ohne formale Kenntnisse in der Informatik benutzt. Aber diese Woche kam mir der Gedanke, dass ich mich nie gefragt habe, wie die FFT die diskrete Fourier-Transformation so schnell berechnet. Ich schüttelte den Staub eines alten Buches über Algorithmen ab, öffnete es und las mit Vergnügen den täuschend einfachen Rechen-Trick, den J.V. Cooley und John Tukey in ihrer klassischen Arbeit von 1965 zu diesem Thema beschrieben hatten.



Das Ziel dieses Beitrags ist es, in den Cooley-Tukey-FFT-Algorithmus einzutauchen, die dazu führenden Symmetrien zu erklären und einige einfache Python-Implementierungen zu zeigen, die die Theorie in der Praxis anwenden. Ich hoffe, dass diese Studie Datenanalysespezialisten wie mir ein vollständigeres Bild davon gibt, was unter der Haube der von uns verwendeten Algorithmen geschieht.

Diskrete Fourier-Transformation

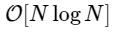
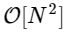
FFT ist schnell ein Algorithmus zur Berechnung der diskreten Fourier-Transformation (DFT), für die direkt berechnet wird . Die DFT hat wie die bekanntere kontinuierliche Version der Fourier-Transformation eine direkte und inverse Form, die wie folgt definiert sind:

Direkte diskrete Fourier-Transformation (DFT):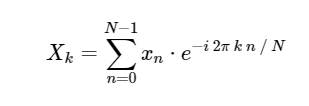



Inverse diskrete Fourier-Transformation (ODPF):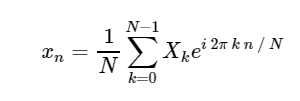



Die Umwandlung von xn → Xk ist eine Übersetzung vom Konfigurationsraum in den Frequenzraum und kann sowohl zur Untersuchung des Signalleistungsspektrums als auch zur Umwandlung bestimmter Aufgaben für eine effizientere Berechnung sehr nützlich sein. Einige Beispiele hierfür finden Sie in Kapitel 10 unseres zukünftigen Buches über Astronomie und Statistik. Dort finden Sie auch Bilder und Quellcode in Python. Ein Beispiel für die Verwendung von FFT zur Vereinfachung der Integration ansonsten komplizierter Differentialgleichungen finden Sie in meinem Beitrag „Lösen der Schrödinger-Gleichung in Python“ .

Aufgrund der Bedeutung von FFT (im Folgenden kann die äquivalente FFT - Fast Fourier Transform verwendet werden) enthält Python in vielen Bereichen viele Standardwerkzeuge und -shells zur Berechnung. Sowohl NumPy als auch SciPy verfügen über Shells aus der äußerst gut getesteten FFTPACK-Bibliothek, die in den scipy.fftpack numpy.fft und scipy.fftpack sind. Die schnellste FFT, die ich kenne, ist das FFTW- Paket, das auch in Python über das PyFFTW- Paket verfügbar ist.

Lassen wir diese Implementierungen jedoch zunächst beiseite und fragen uns, wie wir die FFT in Python von Grund auf neu berechnen können.

Diskrete Fourier-Transformationsberechnung

Der Einfachheit halber werden wir uns nur mit der direkten Konvertierung befassen, da die inverse Transformation auf sehr ähnliche Weise implementiert werden kann. Wenn wir uns den obigen Ausdruck der DFT ansehen, sehen wir, dass dies nichts weiter als eine einfache lineare Operation ist: Multiplizieren der Matrix mit einem Vektor





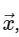
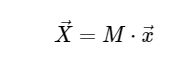
mit Matrix M gegeben



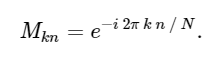
Vor diesem Hintergrund können wir die DFT mithilfe einer einfachen Matrixmultiplikation wie folgt berechnen:

In [1]:

 import numpy as np def DFT_slow(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x) 

Wir können das Ergebnis überprüfen, indem wir es mit der in numpy integrierten FFT-Funktion vergleichen:

In [2]:

 x = np.random.random(1024) np.allclose(DFT_slow(x), np.fft.fft(x)) 

0ut [2]:

True

Um die Langsamkeit unseres Algorithmus zu bestätigen, können wir die Ausführungszeit dieser beiden Ansätze vergleichen:

In [3]:

 %timeit DFT_slow(x) %timeit np.fft.fft(x) 

 10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop 

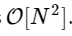
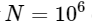
Wir sind mehr als 1000-mal langsamer, was für eine derart vereinfachte Implementierung zu erwarten ist. Das ist aber nicht das Schlimmste. Für einen Eingabevektor der Länge N skaliert der FFT-Algorithmus als während unser langsamer Algorithmus wie skaliert . Dies bedeutet, dass für Wir erwarten, dass die FFT in ungefähr 50 ms abgeschlossen sein wird, während unser langsamer Algorithmus ungefähr 20 Stunden dauern wird!

Wie erreicht die FFT eine solche Beschleunigung? Die Antwort ist, Symmetrie zu verwenden.

Symmetrien in der diskreten Fourier-Transformation

Eines der wichtigsten Werkzeuge beim Erstellen von Algorithmen ist die Verwendung von Aufgabensymmetrien. Wenn Sie analytisch zeigen können, dass ein Teil des Problems einfach mit dem anderen zusammenhängt, können Sie das Teilergebnis nur einmal berechnen und diese Berechnungskosten sparen. Cooley und Tukey verwendeten genau diesen Ansatz, um FFT zu erhalten.
Wir beginnen mit der Frage nach der Bedeutung . Aus unserem obigen Ausdruck:



wo wir die Identität exp [2π in] = 1 verwendet haben, die für jede ganze Zahl n gilt.

Die letzte Zeile zeigt gut die Symmetrieeigenschaft der DFT:



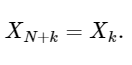
Eine einfache Erweiterung



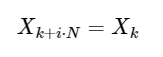
für jede ganze Zahl i. Wie wir unten sehen werden, kann diese Symmetrie verwendet werden, um die DFT viel schneller zu berechnen.

DFT in FFT: Symmetrie verwenden

Cooley und Tukey zeigten, dass FFT-Berechnungen in zwei kleinere Teile unterteilt werden können. Aus der Definition von DFT haben wir:



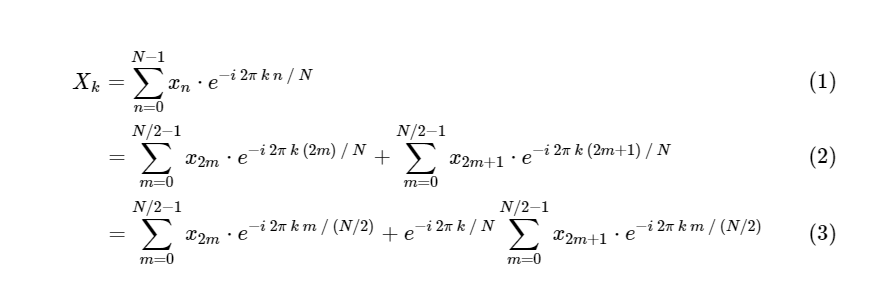
Wir haben eine diskrete Fourier-Transformation in zwei Terme unterteilt, die an sich kleineren diskreten Fourier-Transformationen sehr ähnlich sind, eine für Werte mit einer ungeraden Zahl und eine für Werte mit einer geraden Zahl. Bisher haben wir jedoch keine Rechenzyklen gespeichert. Jeder Term besteht aus (N / 2) ∗ N Berechnungen insgesamt .

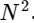
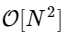
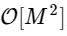
Der Trick besteht darin, unter jeder dieser Bedingungen Symmetrie zu verwenden. Da der Bereich von k 0 ≤ k <N ist und der Bereich von n 0 ≤ n <M≡N / 2 ist, sehen wir aus den obigen Symmetrieeigenschaften, dass wir nur die Hälfte der Berechnungen für jede Teilaufgabe durchführen müssen. Unsere Berechnung ist geworden wobei M zweimal kleiner als N ist.

Es gibt jedoch keinen Grund, sich damit zu befassen: Solange unsere kleineren Fourier-Transformationen ein gerades M haben, können wir diesen „Divide and Conquer“ -Ansatz jedes Mal, wenn sich die Rechenkosten halbieren, erneut anwenden, bis unsere Arrays klein genug sind, sodass die Strategie keine Vorteile mehr bietet. In der asymptotischen Grenze skaliert dieser rekursive Ansatz als O [NlogN].

Dieser rekursive Algorithmus kann sehr schnell in Python implementiert werden, beginnend mit unserem langsamen DFT-Code, wenn die Größe der Unteraufgabe recht klein wird:

In [4]:

 def FFT(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if N % 2 > 0: raise ValueError("size of x must be a power of 2") elif N <= 32: # this cutoff should be optimized return DFT_slow(x) else: X_even = FFT(x[::2]) X_odd = FFT(x[1::2]) factor = np.exp(-2j * np.pi * np.arange(N) / N) return np.concatenate([X_even + factor[:N / 2] * X_odd, X_even + factor[N / 2:] * X_odd]) 

Hier werden wir schnell überprüfen, ob unser Algorithmus das richtige Ergebnis liefert:
In [5]:

 x = np.random.random(1024) np.allclose(FFT(x), np.fft.fft(x)) 

Out [5]:
True

Vergleichen Sie diesen Algorithmus mit unserer langsamen Version:
-In [6]:

 %timeit DFT_slow(x) %timeit FFT(x) %timeit np.fft.fft(x) 

 10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop 

Unsere Berechnung ist schneller als die direkte Version! Darüber hinaus ist unser rekursiver Algorithmus asymptotisch : Wir haben die schnelle Fourier-Transformation implementiert.

Beachten Sie, dass wir immer noch nicht in der Nähe der Geschwindigkeit des in numpy integrierten FFT-Algorithmus sind, und dies sollte erwartet werden. Der FFTPACK-Algorithmus hinter fft numpy ist eine Fortran-Implementierung, die jahrelang verfeinert und optimiert wurde. Darüber hinaus umfasst unsere NumPy-Lösung sowohl die Rekursion des Python-Stacks als auch die Zuweisung vieler temporärer Arrays, wodurch sich die Rechenzeit erhöht.

Eine gute Strategie zur Beschleunigung des Codes bei der Arbeit mit Python / NumPy besteht darin, sich wiederholende Berechnungen nach Möglichkeit zu vektorisieren. Wir können dies tun - löschen Sie dabei unsere rekursiven Funktionsaufrufe, wodurch unsere Python-FFT noch effizienter wird.

Vektorisierte Numpy-Version

Bitte beachten Sie, dass in der obigen rekursiven Implementierung von FFT auf der niedrigsten Rekursionsstufe N / 32 identische Matrixvektorprodukte ausgeführt werden. Die Effektivität unseres Algorithmus wird gewinnen, wenn wir diese Matrixvektorprodukte gleichzeitig als ein einzelnes Matrixmatrixprodukt berechnen. Auf jeder nachfolgenden Rekursionsstufe führen wir auch sich wiederholende Operationen aus, die vektorisiert werden können. NumPy leistet hervorragende Arbeit bei einer solchen Operation, und wir können diese Tatsache nutzen, um diese vektorisierte Version der schnellen Fourier-Transformation zu erstellen:

In [7]:

 def FFT_vectorized(x): """A vectorized, non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2") # N_min here is equivalent to the stopping condition above, # and should be a power of 2 N_min = min(N, 32) # Perform an O[N^2] DFT on all length-N_min sub-problems at once n = np.arange(N_min) k = n[:, None] M = np.exp(-2j * np.pi * n * k / N_min) X = np.dot(M, x.reshape((N_min, -1))) # build-up each level of the recursive calculation all at once while X.shape[0] < N: X_even = X[:, :X.shape[1] / 2] X_odd = X[:, X.shape[1] / 2:] factor = np.exp(-1j * np.pi * np.arange(X.shape[0]) / X.shape[0])[:, None] X = np.vstack([X_even + factor * X_odd, X_even - factor * X_odd]) return X.ravel() 

Obwohl der Algorithmus etwas undurchsichtiger ist, handelt es sich lediglich um eine Neuanordnung der in der rekursiven Version verwendeten Operationen, mit einer Ausnahme: Wir verwenden Symmetrie bei der Berechnung der Koeffizienten und erstellen nur die Hälfte des Arrays. Wieder bestätigen wir, dass unsere Funktion das richtige Ergebnis liefert:

In [8]:

 x = np.random.random(1024) np.allclose(FFT_vectorized(x), np.fft.fft(x)) 

Out [8]:
True

Da unsere Algorithmen viel effizienter werden, können wir ein größeres Array verwenden, um die Zeit zu vergleichen, sodass DFT_slow übrig DFT_slow :
In [9]:

 x = np.random.random(1024 * 16) %timeit FFT(x) %timeit FFT_vectorized(x) %timeit np.fft.fft(x) 

 10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop 

Wir haben unsere Implementierung um eine Größenordnung verbessert! Jetzt sind wir ungefähr zehnmal vom FFTPACK-Benchmark entfernt und verwenden nur ein paar Dutzend Zeilen reines Python + NumPy. Obwohl dies in Bezug auf die Lesbarkeit immer noch nicht rechnerisch konsistent ist, ist die Python-Version dem FFTPACK-Quellcode, den Sie hier anzeigen können, weit überlegen.

Wie erreicht FFTPACK diese letzte Beschleunigung? Im Grunde ist es nur eine Frage der detaillierten Buchhaltung. FFTPACK verbringt viel Zeit damit, Zwischenberechnungen wiederzuverwenden, die wiederverwendet werden können. Unsere zerlumpte Version enthält immer noch überschüssige Speicherzuweisung und Kopieren. In einer einfachen Sprache wie Fortran ist es einfacher, die Speichernutzung zu steuern und zu minimieren. Darüber hinaus kann der Cooley-Tukey-Algorithmus erweitert werden, um Partitionen mit einer anderen Größe als 2 zu verwenden (was wir hier implementiert haben, ist als Cooley-Tukey-Radix-FFT auf der Basis von 2 bekannt). Es können auch andere komplexere FFT-Algorithmen verwendet werden, einschließlich grundlegend unterschiedlicher Ansätze, die auf Faltungsdaten basieren (siehe beispielsweise den Blueshtein-Algorithmus und den Raider-Algorithmus). Die Kombination der oben genannten Erweiterungen und Methoden kann selbst bei Arrays, deren Größe keine Zweierpotenz ist, zu sehr schnellen FFTs führen.

Obwohl Funktionen in reinem Python in der Praxis wahrscheinlich nutzlos sind, hoffe ich, dass sie einen Einblick in das geben, was im Hintergrund der FFT-basierten Datenanalyse geschieht. Als Datenexperten können wir mit der Implementierung der „Black Box“ grundlegender Tools fertig werden, die von unseren algorithmisch orientierten Kollegen erstellt wurden. Ich bin jedoch der festen Überzeugung, dass je besser wir die Algorithmen auf niedriger Ebene verstehen, die wir auf unsere Daten anwenden, desto bessere Praktiken wir werden.

Dieser Beitrag wurde vollständig in IPython Notepad geschrieben. Das vollständige Notizbuch kann hier heruntergeladen oder hier statisch angezeigt werden .

Viele mögen bemerken, dass das Material alles andere als neu ist, aber es scheint uns ziemlich relevant zu sein. Schreiben Sie im Allgemeinen, ob der Artikel nützlich war. Warten auf Ihre Kommentare.