Geekly articles weekly

Erstellung eines formalen Verifizierungssystems von Grund auf neu. Teil 1: Virtuelle Zeichenmaschine in PHP und Python

Die formale Überprüfung ist die Überprüfung eines Programms oder Algorithmus unter Verwendung eines anderen.

Dies ist eine der leistungsstärksten Methoden, mit denen Sie alle Schwachstellen im Programm finden oder nachweisen können, dass sie nicht vorhanden sind.

Eine detailliertere Beschreibung der formalen Überprüfung findet sich am Beispiel der Lösung des Problems von Wolf, Ziege und Kohl in meinem vorherigen Artikel.

In diesem Artikel werde ich von der formalen Überprüfung von Aufgaben zu Programmen übergehen und beschreiben
wie man sie automatisch in formale Regelsysteme umwandelt.

Dafür habe ich mein Analogon einer virtuellen Maschine nach symbolischen Prinzipien geschrieben.

Sie analysiert den Programmcode und übersetzt ihn in ein Gleichungssystem (SMT), das bereits programmgesteuert gelöst werden kann.

Da Informationen zu symbolischen Berechnungen im Internet eher fragmentarisch dargestellt werden,
Ich werde kurz beschreiben, was es ist.

Zeichenberechnungen sind eine Möglichkeit, ein Programm gleichzeitig für eine Vielzahl von Daten auszuführen, und sind das Hauptwerkzeug für die formale Überprüfung von Programmen.

Zum Beispiel können wir die Eingabebedingungen festlegen, unter denen das erste Argument beliebige positive Werte annehmen kann, das zweite negative, das dritte - Null und das Ausgabeargument, zum Beispiel 42.

Symbolische Berechnungen in einem Durchgang geben uns die Antwort. Ist es uns möglich, das gewünschte Ergebnis und ein Beispiel für einen Satz solcher Eingabeparameter zu erhalten? Oder der Beweis, dass es keine solchen Parameter gibt.

Darüber hinaus können wir die Eingabeargumente im Allgemeinen so weit wie möglich festlegen und nur die Ausgabe auswählen, z. B. das Administratorkennwort.

In diesem Fall werden wir alle Schwachstellen des Programms finden oder den Beweis erhalten, dass das Administratorkennwort sicher ist.

Möglicherweise stellen Sie fest, dass die klassische Ausführung eines Programms mit bestimmten Eingabedaten ein Sonderfall eines symbolischen ist.

Daher kann meine Charakter-VM auch im Emulationsmodus einer virtuellen Standardmaschine arbeiten.

In den Kommentaren zum vorherigen Artikel finden Sie eine faire Kritik an der formalen Überprüfung mit einer Diskussion ihrer Schwächen.

Die Hauptprobleme sind wie folgt:

  1. Kombinatorische Explosion, da die formale Verifikation letztendlich auf P = NP beruht
  2. Die Verarbeitung von Aufrufen an das Dateisystem, Netzwerke und andere externe Speicher ist schwieriger zu überprüfen
  3. Fehler in der Spezifikation, wenn der Kunde oder Programmierer eine Sache konzipierte, diese aber in der Arbeitserklärung nicht genau beschrieb.

Infolgedessen wird das Programm überprüft und erfüllt die Spezifikationen, aber es wird überhaupt nicht das tun, was die Entwickler von ihm erwartet haben.

Da ich in diesem Artikel hauptsächlich die Anwendung der formalen Verifizierung in der Praxis betrachte, werde ich meine Stirn noch nicht gegen die Wand schlagen und ein System wählen, bei dem die algorithmische Komplexität und die Anzahl der externen Anrufe minimal sind.

Da intelligente Verträge diesen Anforderungen am besten entsprechen, fiel die Auswahl auf RIDE-Verträge von der Waves-Plattform: Sie sind nicht vollständig und ihre maximale Komplexität ist künstlich begrenzt.

Wir werden sie jedoch nur von der technischen Seite betrachten.

Darüber hinaus ist bei Verträgen eine formelle Überprüfung besonders gefragt: In der Regel ist es unmöglich, einen Vertragsfehler nach seinem Start zu korrigieren.
Und der Preis für solche Fehler kann sehr hoch sein, da häufig große Geldbeträge auf intelligenten Verträgen gespeichert werden.

Meine virtuelle Charaktermaschine ist in PHP und Python geschrieben und verwendet den Z3Prover von Microsoft Research, um die resultierenden SMT-Formeln zu lösen.

Im Kern liegt eine leistungsstarke Multi-Transaktions-Suche, die
ermöglicht es Ihnen, Lösungen oder Schwachstellen zu finden, auch wenn viele Transaktionen erforderlich sind.
Sogar Mythril , eines der mächtigsten symbolischen Frameworks für die Suche nach Ethereum-Schwachstellen, hat diese Funktion erst vor wenigen Monaten hinzugefügt.

Es ist jedoch anzumerken, dass Ätherverträge komplexer sind und die Vollständigkeit von Turing aufweisen.

PHP übersetzt den Quellcode des RIDE-Smart-Vertrags in ein Python-Skript, in dem das Programm in Form eines Systems von Vertragsbedingungen und Bedingungen für ihre mit Z3 SMT kompatiblen Übergänge dargestellt wird:



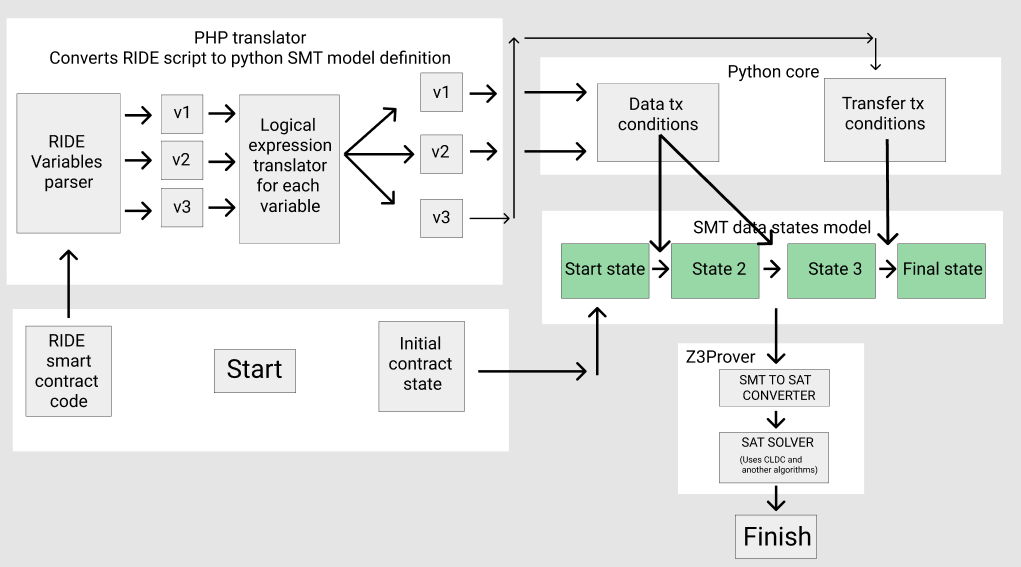
Jetzt werde ich genauer beschreiben, was im Inneren passiert.

Aber zuerst ein paar Worte zur Sprache der intelligenten Verträge RIDE.

Es ist eine funktionale und ausdrucksbasierte Programmiersprache, die wie beabsichtigt faul ist.
RIDE wird isoliert innerhalb der Blockchain ausgeführt und kann Informationen aus dem Speicher extrahieren und schreiben, der der Brieftasche des Benutzers zugeordnet ist.

Sie können jeder Brieftasche einen RIDE-Vertrag hinzufügen, und das Ergebnis der Ausführung ist nur WAHR oder FALSCH.

TRUE bedeutet, dass der Smart-Vertrag die Transaktion zulässt, und FALSE, dass er sie verbietet.
Ein einfaches Beispiel: Ein Skript kann eine Übertragung verbieten, wenn das Brieftaschenguthaben weniger als 100 beträgt.

Als Beispiel nehme ich alle Wolf, Ziege und Kohl, die aber bereits in Form eines intelligenten Vertrags präsentiert wurden.

Der Benutzer kann erst dann Geld von der Brieftasche abheben, auf der der Vertrag bereitgestellt wird, wenn er alle an die andere Seite weiterleitet.

#      let contract = tx.sender let human= extract(getInteger(contract,"human")) let wolf= extract(getInteger(contract,"wolf")) let goat= extract(getInteger(contract,"goat")) let cabbage= extract(getInteger(contract,"cabbage")) #   -,      4 . #           . match tx { case t:DataTransaction => #       let newHuman= extract(getInteger(t.data,"human")) let newWolf= extract(getInteger(t.data,"wolf")) let newGoat= extract(getInteger(t.data,"goat")) let newCabbage= extract(getInteger(t.data,"cabbage")) #0 ,     ,  1    let humanSide= human == 0 || human == 1 let wolfSide= wolf == 0 || wolf == 1 let goatSide= goat == 0 || goat == 1 let cabbageSide= cabbage == 0 || cabbage == 1 let side= humanSide && wolfSide && goatSide && cabbageSide #    ,        . let safeAlone= newGoat != newWolf && newGoat != newCabbage let safe= safeAlone || newGoat == newHuman let humanTravel= human != newHuman #     ,  -   . let t1= humanTravel && newWolf == wolf + 1 && newGoat == goat && newCabbage == cabbage let t2= humanTravel && newWolf == wolf && newGoat == goat + 1 && newCabbage == cabbage let t3= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage + 1 let t4= humanTravel && newWolf == wolf - 1 && newGoat == goat && newCabbage == cabbage let t5= humanTravel && newWolf == wolf && newGoat == goat - 1 && newCabbage == cabbage let t6= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage - 1 let t7= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage let objectTravel = t1 || t2 || t3 || t4 || t5 || t6 || t7 #        . #     1  0,    #  ,        #  -    side && safe && humanTravel && objectTravel case s:TransferTransaction => #             human == 1 && wolf == 1 && goat == 1 && cabbage == 1 #     case _ => false }

PHP extrahiert zunächst alle Variablen in Form ihrer Schlüssel und der entsprechenden Variablen des logischen Ausdrucks aus dem Smart Contract.

 cabbage: extract ( getInteger ( contract , "cabbage" ) ) goat: extract ( getInteger ( contract , "goat" ) ) human: extract ( getInteger ( contract , "human" ) ) wolf: extract ( getInteger ( contract , "wolf" ) ) fState: human== 1 && wolf== 1 && goat== 1 && cabbage== 1 fState: wolf: goat: cabbage: cabbageSide: cabbage== 0 || cabbage== 1 human: extract ( getInteger ( contract , "human" ) ) newGoat: extract ( getInteger ( t.data , "goat" ) ) newHuman: extract ( getInteger ( t.data , "human" ) ) goatSide: goat== 0 || goat== 1 humanSide: human== 0 || human== 1 t7: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage t3: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage + 1 t6: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage - 1 t2: humanTravel && newWolf== wolf && newGoat== goat + 1 && newCabbage== cabbage t5: humanTravel && newWolf== wolf && newGoat== goat - 1 && newCabbage== cabbage t1: humanTravel && newWolf== wolf + 1 && newGoat== goat && newCabbage== cabbage t4: humanTravel && newWolf== wolf - 1 && newGoat== goat && newCabbage== cabbage safeAlone: newGoat != newWolf && newGoat != newCabbage wolfSide: wolf== 0 || wolf== 1 humanTravel: human != newHuman side: humanSide && wolfSide && goatSide && cabbageSide safe: safeAlone || newGoat== newHuman objectTravel: t1 || t2 || t3 || t4 || t5 || t6 || t7

PHP konvertiert sie dann in eine kompatible Python-Systembeschreibung für Z3Prover SMT.
Die Daten werden in einen Zyklus eingeschlossen, in dem die Speichervariablen den Index i, den Transaktionsvariablenindex i + 1 und Variablen mit Ausdrücken erhalten, die die Regeln für den Übergang vom vorherigen zum nächsten Status festlegen.

Dies ist das Herzstück unserer virtuellen Maschine, die eine Suchmaschine für mehrere Transaktionen bietet.

 fState: And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 ) final: fState[Steps] fState: wolf: goat: cabbage: cabbageSide: Or( cabbage[i] == 0 , cabbage[i] == 1 ) goatSide: Or( goat[i] == 0 , goat[i] == 1 ) humanSide: Or( human[i] == 0 , human[i] == 1 ) t7: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) t3: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] + 1 ) t6: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] - 1 ) t2: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage == cabbage[i] ) t5: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage == cabbage[i] ) t1: And( And( And( humanTravel[i] , wolf == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) t4: And( And( And( humanTravel[i] , wolf == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) safeAlone: And( goat[i+1] != wolf , goat[i+1] != cabbage ) wolfSide: Or( wolf[i] == 0 , wolf[i] == 1 ) humanTravel: human[i] != human[i+1] side: And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) safe: Or( safeAlone[i] , goat[i+1] == human[i+1] ) objectTravel: Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) data: And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] )

Bedingungen werden sortiert und in eine Skriptvorlage eingefügt, die das SMT-System in Python beschreibt.

Leere Vorlage
 import json from z3 import * s = Solver() Steps=7 Num= Steps+1 $code$ #template, only start rest s.add(data + start) #template s.add(final) ind = 0 f = open("/var/www/html/all/bin/python/log.txt", "a") while s.check() == sat: ind = ind +1 print ind m = s.model() print m print "traversing model..." #for d in m.decls(): #print "%s = %s" % (d.name(), m[d]) f.write(str(m)) f.write("\n\n") exit() #s.add(Or(goat[0] != s.model()[data[0]] )) # prevent next model from using the same assignment as a previous model print "Total solution number: " print ind f.close()


Für den letzten Status aus der gesamten Kette gelten die Regeln, die im Abschnitt Übertragungstransaktion angegeben sind.

Daher wird Z3Prover nach solchen Bedingungen suchen, die es Ihnen schließlich ermöglichen, Geld vom Vertrag abzuheben.

Als Ergebnis erhalten wir automatisch ein voll funktionsfähiges SMT-Modell unseres Vertrags.
Sie können sehen, dass es dem Modell aus meinem vorherigen Artikel, den ich manuell geschrieben habe, sehr ähnlich ist.

Vorlage abgeschlossen
 import json from z3 import * s = Solver() Steps=7 Num= Steps+1 human = [ Int('human_%i' % (i + 1)) for i in range(Num) ] wolf = [ Int('wolf_%i' % (i + 1)) for i in range(Num) ] goat = [ Int('goat_%i' % (i + 1)) for i in range(Num) ] cabbage = [ Int('cabbage_%i' % (i + 1)) for i in range(Num) ] nothing= [ And( human[i] == human[i+1], wolf[i] == wolf[i+1], goat[i] == goat[i+1], cabbage[i] == cabbage[i+1] ) for i in range(Num-1) ] start= [ human[0] == 1, wolf[0] == 0, goat[0] == 1, cabbage[0] == 0 ] safeAlone= [ And( goat[i+1] != wolf[i+1] , goat[i+1] != cabbage[i+1] ) for i in range(Num-1) ] safe= [ Or( safeAlone[i] , goat[i+1] == human[i+1] ) for i in range(Num-1) ] humanTravel= [ human[i] != human[i+1] for i in range(Num-1) ] cabbageSide= [ Or( cabbage[i] == 0 , cabbage[i] == 1 ) for i in range(Num-1) ] goatSide= [ Or( goat[i] == 0 , goat[i] == 1 ) for i in range(Num-1) ] humanSide= [ Or( human[i] == 0 , human[i] == 1 ) for i in range(Num-1) ] t7= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t3= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] + 1 ) for i in range(Num-1) ] t6= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] - 1 ) for i in range(Num-1) ] t2= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t5= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t1= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t4= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] wolfSide= [ Or( wolf[i] == 0 , wolf[i] == 1 ) for i in range(Num-1) ] side= [ And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) for i in range(Num-1) ] objectTravel= [ Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) for i in range(Num-1) ] data= [ Or( And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] ) , nothing[i]) for i in range(Num-1) ] fState= And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 ) final= fState #template, only start rest s.add(data + start) #template s.add(final) ind = 0 f = open("/var/www/html/all/bin/python/log.txt", "a") while s.check() == sat: ind = ind +1 print ind m = s.model() print m print "traversing model..." #for d in m.decls(): #print "%s = %s" % (d.name(), m[d]) f.write(str(m)) f.write("\n\n") exit() #s.add(Or(goat[0] != s.model()[data[0]] )) # prevent next model from using the same assignment as a previous model print "Total solution number: " print ind f.close()


Nach dem Start löst Z3Prover einen intelligenten Vertrag und zeigt uns eine Transaktionskette an, mit der wir Geld abheben können:

 Winning transaction chain found: Data transaction: human= 0, wolf= 0, goat= 1, cabbage= 0 Data transaction: human= 1, wolf= 0, goat= 1, cabbage= 1 Data transaction: human= 0, wolf= 0, goat= 0, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 0, cabbage= 1 Data transaction: human= 0, wolf= 1, goat= 0, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1 Transfer transaction

Zusätzlich zum Speditionsvertrag können Sie mit Ihren eigenen Verträgen experimentieren oder dieses einfache Beispiel ausprobieren, das in 2 Transaktionen gelöst wird.

 let contract = tx.sender let a= extract(getInteger(contract,"a")) let b= extract(getInteger(contract,"b")) let c= extract(getInteger(contract,"c")) let d= extract(getInteger(contract,"d")) match tx { case t:DataTransaction => let na= extract(getInteger(t.data,"a")) let nb= extract(getInteger(t.data,"b")) let nc= extract(getInteger(t.data,"c")) let nd= extract(getInteger(t.data,"d")) nd == 0 || a == 100 - 5 case s:TransferTransaction => ( a + b - c ) * d == 12 case _ => true }

Da dies die allererste Version ist, ist die Syntax sehr begrenzt und es können Fehler auftreten.
In den folgenden Artikeln möchte ich die weitere Entwicklung von VM hervorheben und zeigen, wie es möglich ist, mit seiner Hilfe formal verifizierte intelligente Verträge zu erstellen und nicht nur zu lösen.

Eine symbolische virtuelle Maschine ist unter http://2.59.42.98/hyperbox/ verfügbar.
Quellen sind auf github verfügbar: http://github.com/scp1001/hyperbox
Die gesamte VM-Logik ist in zwei Dateien enthalten: hyperbox.php und hyperbox2.php

Source: https://habr.com/ru/post/de450016/

More articles:


All Articles