Ein Mathe-Duo kartierte ein endloses Gebiet mit minimalen Oberflächen

Ein paar Mathematiker, die auf einer vor 30 Jahren wenig bekannten mathematischen Theorie basierten, zeigten, dass minimale Oberflächen, die einem Seifenfilm ähneln, in großer Zahl auf einer Vielzahl von Figuren erscheinen

Ende 2011 hörte Brian White gelegentlich ein Klopfen an der Tür seines Büros in Stanford. Draußen warteten in diesen Augenblicken zwei junge Mathematiker auf ihn, Fernando Coda Marquez und Andre Nevis , die immer die gleiche Frage hatten: Hätte White ein paar Minuten Zeit, um einen der dunklen Teile einer wenig bekannten Dissertation für mehrere hundert herauszufinden Seiten vor dreißig Jahren geschrieben?

Die von John Pitts verfasste Dissertation präsentierte einen leistungsstarken Mechanismus zur Konstruktion minimaler Oberflächen - Strukturen ähnlich wie Seifenfilme und Blasen - in einer Vielzahl von Formen. Wenn eine minimale Oberfläche auf einer Figur konstruiert werden kann, ermöglicht letztere die Untersuchung der Geometrie des sie umgebenden Raums. Solche Oberflächen treten bei verschiedenen wissenschaftlichen Problemen auf, von der Untersuchung von Schwarzen Löchern bis zur Entwicklung von Biomolekülen.

Und doch ist Pitts 'Dissertation in all den Jahren außerhalb der Aufmerksamkeit der Wissenschaftler gefallen - vielleicht weil sie unglaublich schwer zu lesen war. Marquez und Nevis waren überzeugt, dass darin ein großes Potenzial steckt. "Es war uns klar, dass diese Theorie völlig unterschätzt wurde und unbemerkt blieb", sagte Nevis, der jetzt Professor an der Universität von Chicago ist.

Obwohl White das Paar nie gefragt hat, warum sie an Pitts 'Arbeit interessiert sind, gaben sie jedes Mal an, dass ihr Interesse "rein akademisch" sei, sagte Nevis. Sie hatten jedoch ein klares Ziel - Wilmores Hypothese vor 50 Jahren zu beweisen, die sich mit dem Problem befasst, die bestmögliche Donutform zu finden (Details später). Nachdem Marquez und Nevis drei Monate lang mit den Ideen aus Pitts 'Dissertation zu kämpfen hatten, erreichten sie ihr Ziel und erhielten viele Auszeichnungen und positive Bewertungen.

In den letzten Jahren konnten sie Pitts Ideen jedoch weiter vorantreiben. Pitts hat mit seinem Kurator Frederick Almgren einen Weg gefunden, um sicherzustellen, dass jede Figur in einer kleinen Anzahl von Dimensionen mindestens eine Mindestfläche hat. Nun haben Marquez und Nevis anhand der Kohorte junger Mathematiker, die sich um sie versammelt haben, basierend auf den Ideen von Almgren und Pitts gezeigt, dass diese Formen im allgemeinen Fall viele minimale Oberflächen enthalten sollten - unendlich viele Oberflächen, die sich in allen Ecken der Figuren drängen und drängen. "Dies ist ein großer Durchbruch", schrieb uns die berühmte Geometerin Karen Uhlenbeck von der University of Texas in einer E-Mail.

"Es ist sehr aufwändig, eine einzige minimale Oberfläche zu schaffen", sagte Richard Shoin von der University of California in Irvine, der Nevis vor etwa 15 Jahren beriet. "Die Tatsache, dass es so viele von ihnen gibt, ist erstaunlich."

Diese Renaissance der Theorie von Almgren und Pitts hat in den letzten Jahren zu einer Explosion der Aktivität geführt. "Die Ergebnisse sind so schnell und in so großer Zahl, dass es schwierig ist, sie im Auge zu behalten", sagte White. "Es scheint mir sehr interessant und wunderbar."

Markierung der Bergkette

Tauchen Sie den gekrümmten Draht in eine Seifenlösung oder blasen Sie eine Seifenblase, und die Flüssigkeit bildet schnell die Oberfläche des kleinstmöglichen Bereichs. Die Geometrie dieser minimalen Flächen beschäftigt Mathematiker seit Hunderten von Jahren. Sie treten in verschiedenen Bereichen auf, von der Architektur, in der die minimale Oberfläche die Gestaltung von Dächern und anderen Strukturen inspiriert, bis hin zur Schaffung von Mikropartikeln für die Arzneimittelabgabe. Als ein Wissenschaftlerteam vor fünf Jahren poröse Moleküle schuf , die Medikamente oder Hormone in sich tragen können, stellten sie fest, dass einige Moleküle die Form einer Gyroid hatten , einer sich endlos wiederholenden Oberfläche, von der einige Teile einem Seifenfilm ähneln.

Technisch gesehen betrachten Mathematiker nur Seifenfilme auf einem Draht als Oberflächen mit einer minimalen Oberfläche, aber keine Seifenblasen, da in einem abstrakten Raum, in dem keine Luftmoleküle vorhanden sind, die Blase bis zu einem Punkt entleert würde. Der Film auf dem Draht befriedigt jedoch die Mathematiker nicht vollständig. Sein innerer Teil ist eine glatte Oberfläche, aber sein Draht bricht scharf ab. Es ist logisch zu überlegen, ob es möglich ist, diese Oberfläche über die Grenzen der Drahtgrenzen hinaus zu erweitern, so dass sie in jedem einzelnen Bereich weiterhin wie ein Seifenfilm aussieht. Manchmal ist dies möglich und die Oberfläche erstreckt sich bis ins Unendliche. Manchmal kommt die Oberfläche zurück und schneidet sich unbeholfen mit sich selbst oder stößt auf andere Schwierigkeiten.


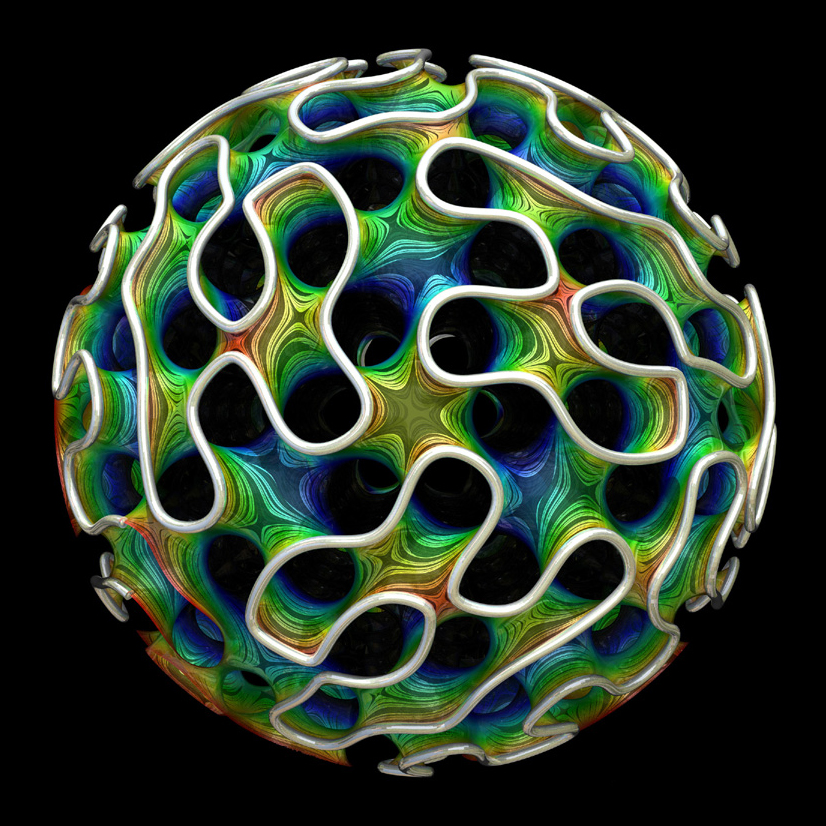Gyroid - eine Art von Mindestoberfläche, die während des Entwurfs von Mikropartikeln für die Arzneimittelabgabe auftrat

Im gewöhnlichen Raum erschöpft dies alle Möglichkeiten. Aber Mathematiker und andere Wissenschaftler betrachten oft andere Welten, die sich von dem unendlichen dreidimensionalen Raum unterscheiden, an den wir gewöhnt sind - gekrümmt oder endlich, wie dreidimensionale Analogien einer Kugel oder Oberfläche eines Torus. Solche Figuren haben neue interessante Möglichkeiten: minimale Oberflächen, die sich auf sich selbst biegen und in eine geschlossene endgültige Figur einrasten, die keine Drahtstütze benötigt.

In der Relativitätstheorie spielen diese endlichen Minimalflächen die Rolle des Ereignishorizonts der Schwarzen Löcher. Und wenn sie auf einer Figur zu finden sind, hilft dies den Mathematikern, ihre Geometrie von verschiedenen Seiten zu betrachten: Sie geben eine Vorlage zum Schneiden der Figur (oder des Verteilers ) in potenziell einfachere Teile, sie zeigen Bereiche mit positiver Krümmung innerhalb des Verteilers an - in Abschnitte, nach innen krümmen, wie eine Kugel oder ein schwarzes Loch, im Gegensatz zu nach außen krümmen.

"Wir wissen wenig über Verteiler mit positiver Krümmung", sagte Shoin.

Es ist jedoch oft schwierig, das Vorhandensein einer minimalen Oberfläche innerhalb einer Figur nachzuweisen. Um zu verstehen, warum dies so ist, betrachten Sie eine zweidimensionale Version dieses Problems. Die Frage, die minimale Oberfläche zu finden, ist in jeder Dimension sinnvoll: Mathematiker betrachten die Oberfläche einfach als eine Form, deren Dimension um eins kleiner ist als der Raum, in dem sie lebt. In einer zweidimensionalen Welt sind die „geodätischen“ Kurven, die aus den kürzesten Wegen bestehen, die nahegelegene Punkte verbinden, die minimale Oberfläche.

Finden Sie für einige zweidimensionale Figuren leicht geodätische Kurven, die in einer endlichen Schleife geschlossen sind. Nehmen Sie die Oberfläche eines Torus - nicht unbedingt eben und symmetrisch - lassen Sie ihn Unregelmäßigkeiten und Ausbuchtungen aufweisen. Wenn wir einen solchen Donut mit einem Gummiband umwickeln, das durch seine Mitte verläuft, können wir uns vorstellen, wie wir ihn festziehen und in verschiedene mögliche Positionen verschieben. Eine davon wird die kürzeste sein - es wird per Definition eine geodätische Kurve sein.



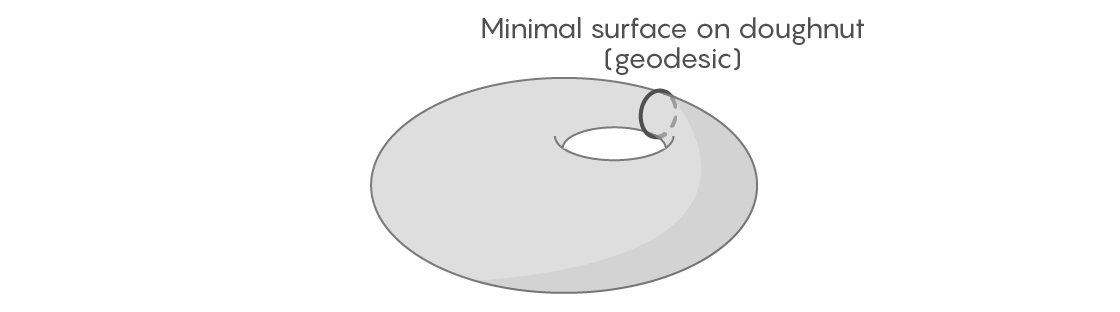
Aber wenn die Kugel unsere Figur ist, wird dieser Ansatz nicht mehr funktionieren. Auf einer perfekt flachen Kugel ist es leicht, eine geodätische Kurve zu finden - es wird der Äquator und andere volle Kreise sein. Auf einer unebenen Kugel, zum Beispiel auf der Erdoberfläche, ist jedoch nicht klar, wohin die geodätischen Kurven führen und ob eine von ihnen in einer Schleife geschlossen ist. Sie können sich vorstellen, wie wir die Erde mit einem Gummiband umwickeln, wie im Fall eines Donuts. Wenn Sie es jedoch bewegen und versuchen, es zu verkürzen, schrumpft es auf einen Punkt, da die Kugel im Gegensatz zu einem Donut kein Loch hat, an dem sich das Gummiband festhalten kann.

Dieses Fiasko mit einem Gummiband ist jedoch mit dem Keim des Erfolgs behaftet. Wenn der Äquator einer runden Kugel von einem elastischen Band abgefangen wird, wird er durch die einzige Möglichkeit, ihn zu verschieben - um Wellen hinzuzufügen - länger. Wenn Sie es anders bewegen, nach oben oder unten auf einen neuen Breitengrad, wird es kürzer. Daher ist der Äquator von einem Standpunkt aus die kürzeste und vom anderen die längste Kurve.

Dies macht den Äquator zum Sattel des Gebirgspasses, zum höchsten Punkt auf der einen Seite (vom Weg durch die Berge) und zum niedrigsten auf der anderen Seite (vom Weg zu den nahe gelegenen Gipfeln). Und das ist nicht nur eine schwache Analogie: Minimalflächen erweisen sich in der Regel als solche Sättel, aber ihre Gebirgszüge leben in einer Welt, die viel schwerer zu visualisieren ist.



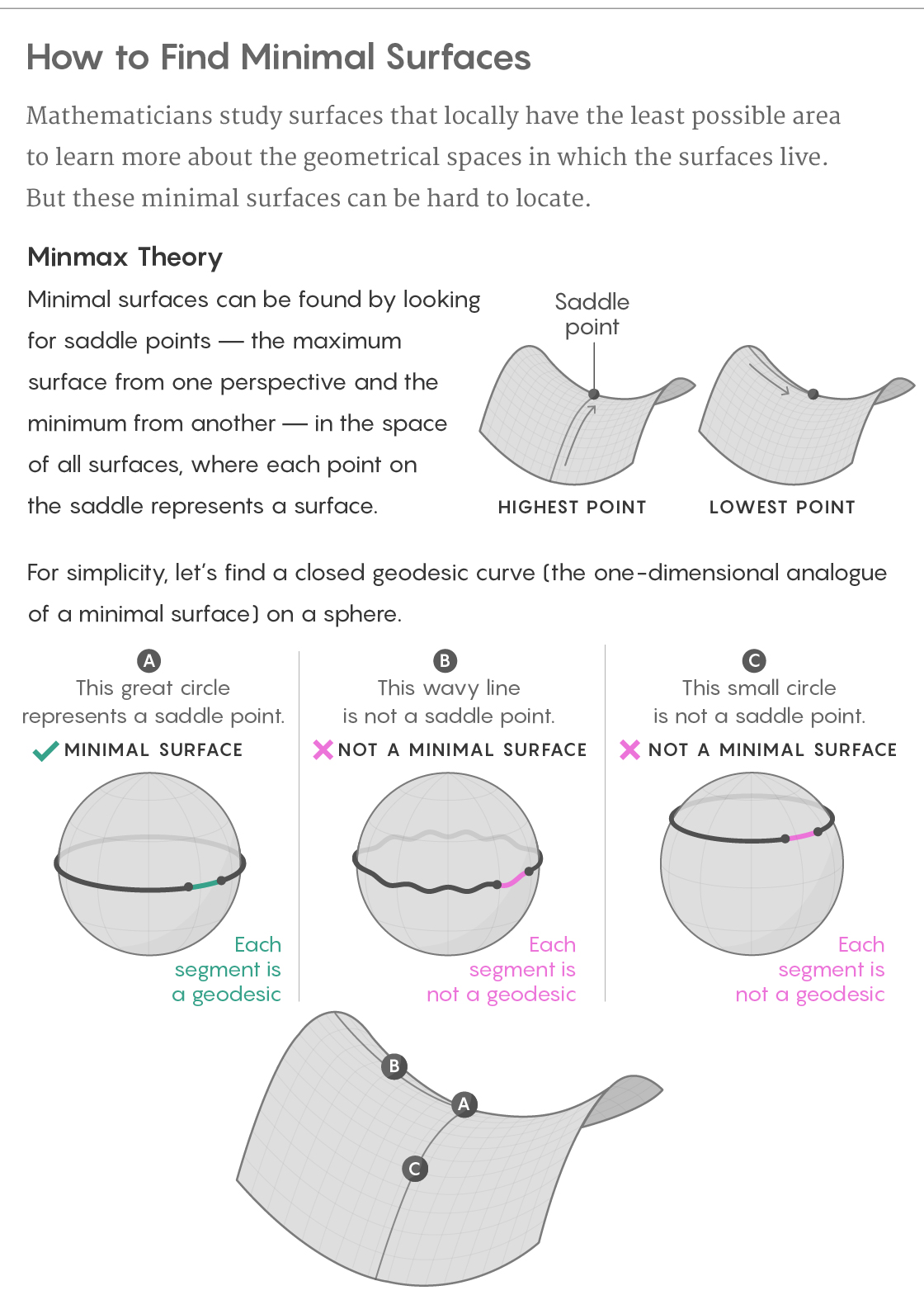
Wenn wir die minimale Oberfläche einer Figur bestimmen, können wir eine neue Welt betrachten, die aus allen möglichen endlichen Flächen besteht, die in dieser Figur existieren - wir werden sie die „Oberfläche von Flächen“ nennen. Jeder Punkt des Oberflächenraums entspricht der gesamten Oberfläche der Originalfigur. Dann können wir die Fläche jeder Oberfläche als die Höhe des entsprechenden Punktes im Raum der Oberflächen betrachten, wodurch unsere Welt eine natürliche Topographie haben wird. Die Suche nach minimalen Oberflächen auf der Originalfigur wird zur Suche nach Sätteln im Oberflächenraum.

1917 verwendete George David Birkhoff diesen Ansatz, um zu zeigen, dass jede Kugel, holprig oder glatt, eine geschlossene geodätische Kurve haben muss. Ungefähr sechs Jahrzehnte später erweiterten Almgren und Pitts meisterhaft Birkhoffs Ideen, indem sie die Oberflächentopographie von Oberflächen auf allen endlichen Figuren in Dimensionen von drei bis sieben markierten, und verwendeten diese Topographie dann, um zu beweisen, dass solche Figuren immer mindestens eine geschlossene minimale Oberfläche haben. Pitts ' Dissertation von 1981 über diese Minmax-Theorie - so genannt, weil der Sattel sowohl ein Minimum als auch ein Maximum ist - war "absolut erstaunlich", sagte Nevis.

Es war jedoch äußerst komplex. Nur wenige Menschen verstanden die Nuancen der Theorie, und einige Mathematiker, die sie studierten, behaupteten, sie sei nicht vollständig bestätigt worden, sagte Shoin. "Ich glaube nicht, dass es Zweifel gab, dass es äußerst interessant und wichtig war", sagte er. "Aber es war unklar, wie voll es war."

Die Arbeit an der Minmax-Theorie wurde allmählich zunichte gemacht. "Pitts 'Arbeit wurde von der mathematischen Gemeinschaft seit etwa 30 Jahren vergessen", sagte Nevis. Sie wurde nicht wiederbelebt, bis Nevis und Marquez sich 2006 im Aufzug des mathematischen Gebäudes der Princeton University trafen.

Über den Gebirgspass

In diesem Moment kam Marquez in Princeton an, um einen Vortrag zu halten; Nevis bekam dort kurz nach der Promotion einen Job. Beide hatten Portugiesisch als Muttersprache (Marquez stammte aus Brasilien und Nevis aus Portugal) und fanden leicht eine gemeinsame Sprache. „Dann habe ich zum ersten Mal mit ihm gesprochen, aber er hat mit mir gesprochen, als wären wir seit 10 Jahren befreundet“, erinnert sich Marquez, jetzt Professor an der Princeton University.

Dann stellten sie fest, dass die Diskussion mathematischer Ideen für sie genauso selbstverständlich war. Sie haben unterschiedliche Stile: Marquez ist ruhiger und Nevis ist intensiver. Dies war jedoch ein Plus für sie. "Es ist sehr selten, jemanden zu finden, der Sie so gut ergänzt", sagte Marquez.

Beide waren bestrebt, ein komplexes mathematisches Problem zu finden, in das sie eintauchen konnten. Mehrere Jahre lang warf das Paar jedes Mal Ideen ein, wenn sich ihre Wege kreuzten, um „zu sehen, was sich verzögerte“, sagte Nevis. "Wir hatten eine Million Ideen, und als Ergebnis wurde eine davon herausgefiltert und in etwas Formiertes verwandelt."

Das herausgefilterte Problem stellte sich als das berühmte Problem der „Wilmore-Hypothese“ heraus. Sie schlägt vor, eine Torusform zu finden, die die als Willmore-Energie bekannte Größe minimiert und grob gesagt den Unterschied zwischen einer bestimmten Form und einer kreisförmigen Kugel misst. 1965 schlug Wilmore vor, dass es sich um den rundesten Donut mit einer besonders symmetrischen Form handeln würde, der als Cliffords Torus bekannt ist. Trotz vieler Versuche konnte die Hypothese jedoch niemandem bewiesen werden.


Marquez (links) und Nevis

Marquez und Nevis entwickelten einen vielversprechenden Ansatz, aber damit er funktionierte, brauchten sie die letzte Zutat: die Minimax-Theorie. Sie dachten, dass es zwei bis drei Wochen dauern würde, diese Theorie zu beherrschen und das endgültige Werk zu schreiben - bis sie das Buch Pitts aufschlugen. „Wir waren schockiert - worum geht es? - sagte Nevis. "Das Buch war unglaublich trocken."

Separate Theoreme wuchsen auf vielen Seiten - und dies war nur eine Beschreibung der Theoreme, nicht deren Beweis. Der Hauptsatz war einfach schwer zu finden. "Ich erinnere mich, wie Fernando in mein Büro kam und sagte: Ich habe die Aussage des Satzes gefunden!" - sagte Nevis.


Thor Clifford

Als sie feststeckten, machten sie Poker und baten White um Hilfe, eine der wenigen Personen, die den größten Teil von Pitts 'Arbeit verstanden (obwohl White selbst diese Gespräche als „blind, führend blind“ beschrieb; Pitts selbst, Professor an der A & M University of Texas, schloss sein Studium ab schreibe Arbeiten zur Theorie des Minmax vor einigen Jahrzehnten). „Wir waren unglaublich motiviert und konnten durchbrechen“, erinnert sich Nevis. "Aber das war keine Aufgabe für schwache Nerven."

Als Marquez und Nevis ihren Beweis für Wilmores Hypothese abgeschlossen hatten, verstanden sie die Minmax-Theorie besser als jeder andere Mathematiker. Sie waren überzeugt, dass sein Potenzial weit über die Aussage der Hypothese hinausgeht. "Wir wussten, dass wir eine sehr mächtige Theorie hatten", sagte Nevis. - Jedes Mal, wenn Sie die Methode verwenden, um ein bestimmtes Ergebnis zu beweisen, das lange offen geblieben ist, verstehen Sie, dass etwas darin enthalten ist. Dies legt nahe, dass es sich lohnt, weiter zu graben. "

Das Minmax-Diagramm von Almgren und Pitts erzeugt nicht nur einen Sattel, sondern eine unendliche Anzahl von ihnen. Theoretisch sollte dies einer unendlichen Anzahl von Minimalflächen der ursprünglichen Form entsprechen. Almgren und Pitts konnten jedoch nicht zeigen, dass die auf diese Weise erhaltenen minimalen Oberflächen unterschiedlich waren. Das einzige, was definitiv gesagt werden konnte, war, dass jede Figur mindestens eine minimale Oberfläche hatte.

Danach "hat die Entwicklung des Themas praktisch aufgehört", sagte Nevis. "Es war das beste Ergebnis seit mehr als 30 Jahren."

Eine neue Zutat wurde benötigt und Marquez und Nevis fanden sie. Die endlose Liste der Minmax-Oberflächen, wie sie 2016 gezeigt wurde, verhält sich genauso wie die Frequenzen der Trommel.

Der Mathematiker Deutsch Weil aus dem Jahr 1911 zeigte, dass die Grundfrequenzen der Trommel eine unerwartete Eigenschaft haben: Grob gesagt hängen hohe Frequenzen nur von der Lautstärke der Trommel und nicht von ihrer Form ab. Marquez und Nevis zeigten zusammen mit Eugene Lekumovich vom Massachusetts Institute of Technology, dass Minmax-Oberflächen ein mathematisches Gesetz erfüllen, das dem Gesetz der Trommelfrequenzen ähnlich ist. Insbesondere werden Oberflächen grob durch den Raum bestimmt, in dem sie leben, und nicht durch seine Form.

Dieses Ergebnis, das der vor einigen Jahrzehnten vorgebrachten Hypothese ein Ende setzte, ermöglichte es Marquez und Nevis 2017 zu zeigen - diesmal unterstützt von Kay Air von der Universität Tokio -, dass die Liste der Minmax für die meisten Zahlen eine unendliche Anzahl verschiedener Minimalflächen enthält. Darüber hinaus zeigten sie, dass diese Oberflächen „dicht“ sind: Sie erscheinen neben jedem Punkt im umgebenden Raum. Die Intuition, die diese Schlussfolgerung stützt, ist, dass das Raumvolumen, um die Bereiche des Ortes minimaler Oberflächen zu bestimmen, das gesamte Volumen irgendwie „sehen“ muss. Und das "sagt, dass diese Jungs in all ihrer Vielfalt sind", sagte Marquez.

Ein paar Monate später zeigte dieses Paar zusammen mit dem Marques-Doktoranden Antoine Sun , dass Sie, wenn Sie die Liste der Minmax-Oberflächen durchgehen, sehen, dass sie den Raum gleichmäßig ausfüllen - was Mathematiker als "Gleichverteilung" bezeichnen, erscheint.

"Als ich hörte, dass sie gleichmäßig verteilt waren, war ich erstaunt", sagte White. "Es schien, dass die Menschen in meinem Leben kein solches Ergebnis hätten nachweisen können."

In den letzten Jahren haben sich mehrere weitere Mathematiker der Frage angeschlossen. Zum Beispiel hat Xin Zhou von der University of California in Santa Barbara im Januar auf der Grundlage früherer Arbeiten von Marquez und Nevis bewiesen, dass sich für die meisten Figuren alle minimalen Flächen auf der Almgren- und Pitts-Liste voneinander unterscheiden, was einen schönen Punkt in diesem Thema darstellt. "Dies schließt dieses Thema, das seit den Tagen von Almgren und Pitts in den 80er Jahren geöffnet ist, wirklich gut ab", sagte White.

Diese Ergebnisfamilie berücksichtigt fast jede Figur in Dimensionen von drei bis sieben - mit Ausnahme der glattesten Formen, egal wie intuitiv sie auch sein mögen. Im vergangenen Juni konnte Sunn jedoch nachweisen, dass jede Figur in diesen Dimensionen, einschließlich der rundesten, unendlich viele geschlossene Minimalflächen aufweist, was eine weitere Hypothese bestätigt, die mehrere Jahrzehnte alt ist.

Es ist noch unklar, ob sich die Dichte und die Gleichverteilung so gleichmäßig verhalten und wie die Minmax-Theorie nicht in kompakten Verteilern oder in acht oder mehr Dimensionen funktioniert (die neue Arbeit hat jedoch auch hier einige Erfolge erzielt). Mathematiker sagen voraus, dass wir viele Fragen früher beantworten können, als es schien.

"Alles entwickelt sich extrem schnell", sagte Nevis. "Jede Woche schaue ich mir die Site mit Arxiv-Preprints an und sehe dort, wie jemand etwas anderes entschieden hat."

Aus einer Sicht markieren diese Arbeiten das Ende - oder das Ende - einer Geschichte, die seit fast vier Jahrzehnten in ihrem unvollendeten Zustand hängt. Dies ist aber auch ein neuer Anfang: Mathematiker beginnen gerade zu verstehen, dass diese neuen Ideen zu minimalen Oberflächen uns über die Räume erzählen können, in denen sie leben.

"Ich kann davon ausgehen, dass bald weitere interessante Möglichkeiten zur Anwendung dieses Wissens auftauchen werden, aber was genau kann ich definitiv nicht sagen", sagte Shoin. "Ich bin sicher, dass dies eine der Hauptrichtungen in der Geometrie sein wird."