Geekly articles weekly

Mein numerischer Test der Absolute Rates-Hypothese

Hallo Habr!

Diese Veröffentlichung erschien mir interessant: Wir erhalten absolute Wechselkurse aus gepaarten Wechselkursen, und ich wollte die Fähigkeit testen, diesen aaaabsoluten Wechselkurs durch numerische Modellierung zu ermitteln, wobei die lineare Algebra im Allgemeinen aufgegeben wird.



Die Ergebnisse waren interessant.

Das Experiment wird klein sein: 4 Währungen, 6 Währungspaare. Für jedes Paar eine Kursmessung.

Also fangen wir an


Die Hypothese ist, dass der Wert einer Währung als ein Wert ausgedrückt werden kann, der den Wert anderer Währungen berücksichtigt, in denen er notiert ist, während andere Währungen selbst im Wert aller anderen Währungen ausgedrückt werden. Dies ist eine interessante rekursive Aufgabe.

Es gibt 4 Währungen:

  • usd
  • eur
  • chf
  • gbp

Für sie wurden die Währungspaare gewählt:

  • eurusd
  • gbpusd
  • eurchf
  • eurgbp
  • gbpchf
  • usdchf

Bitte beachten Sie, dass wenn die Anzahl der Währungen n = 4 ist, die Anzahl der Paare k = (n ^ 2 - n) / 2 = 6 ist. Es macht keinen Sinn, nach usdeur zu suchen, wenn eurusd angegeben ist ...

Zum Zeitpunkt t wurde der Wechselkurs eines der Anbieter gemessen:



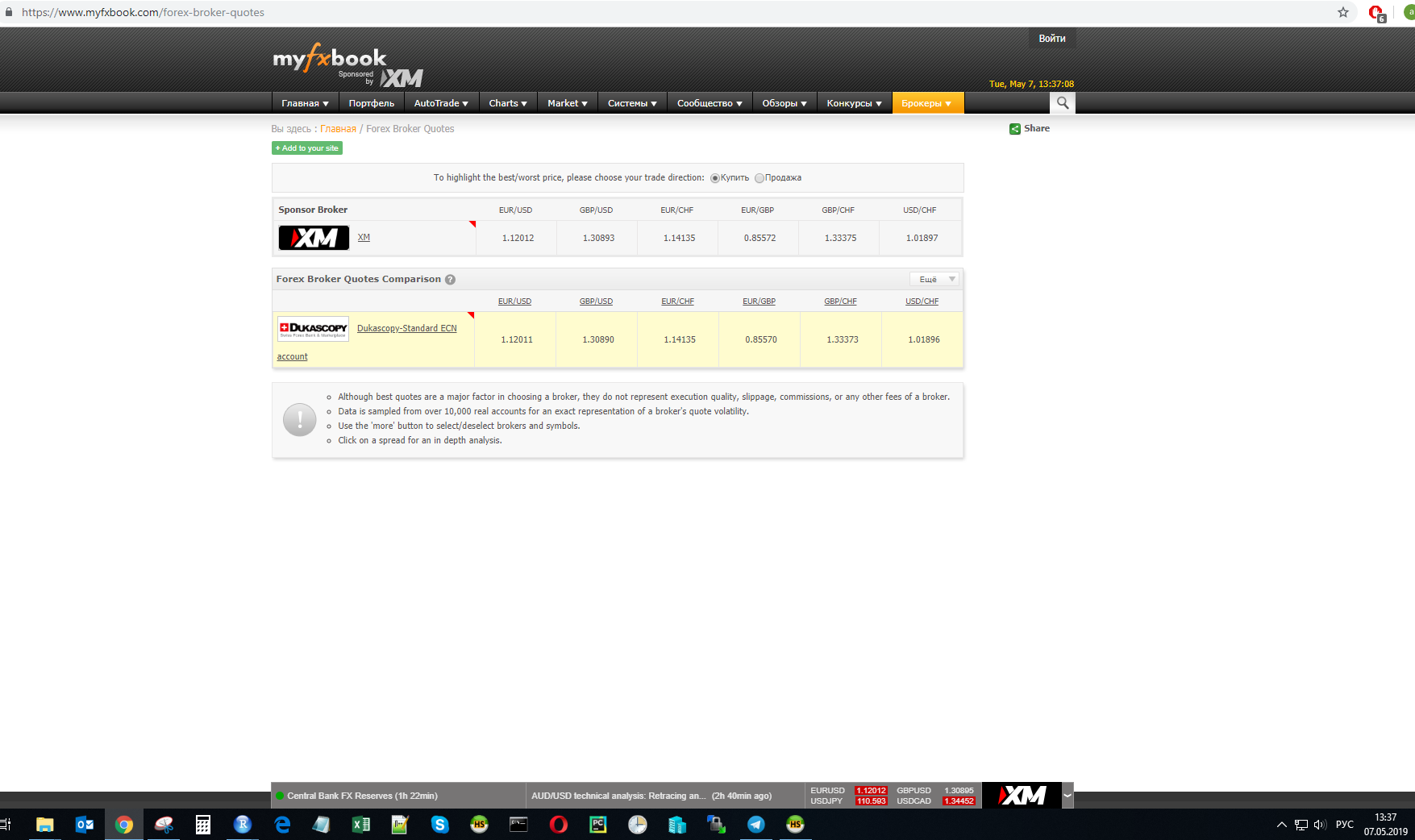
Für diese Werte werden Berechnungen durchgeführt.

Mathe


Ich löse das Problem, indem ich den Gradienten der Verlustfunktion, die im Wesentlichen ein Gleichungssystem ist, analytisch nehme.

Der Experimentcode wird in R sein:

#set.seed(111) usd <- runif(1) eur <- runif(1) chf <- runif(1) gbp <- runif(1) # snapshot of values at time t eurusd <- 1.12012 gbpusd <- 1.30890 eurchf <- 1.14135 eurgbp <- 0.85570 gbpchf <- 1.33373 usdchf <- 1.01896 ## symbolic task ------------ express <- expression( (eurusd - eur / usd) ^ 2 + (gbpusd - gbp / usd) ^ 2 + (eurchf - eur / chf) ^ 2 + (eurgbp - eur / gbp) ^ 2 + (gbpchf - gbp / chf) ^ 2 + (usdchf - usd / chf) ^ 2 ) eval(express) x = 'usd' D(express, x) eval(D(express, x))

R ermöglicht die Verwendung von stats :: D, um eine Ableitung einer Funktion zu erhalten. Wenn wir zum Beispiel nach der USD-Währung differenzieren möchten, erhalten wir den Ausdruck:
2 * (eur / usd ^ 2 * (eurusd - eur / usd)) + 2 * (gbp / usd ^ 2 * (gbpusd -
gbp / usd)) - 2 * (1 / chf * (usdchf - usd / chf))
Um den Wert der Express-Funktion zu reduzieren, führen wir einen Gradientenabstieg durch und es ist sofort klar (wir sehen quadratische Unterschiede), dass der Mindestwert Null ist, was wir brauchen.

 -deriv_vals * lr

Der Gradientenabstiegsschritt wird durch den Parameter lr gesteuert und dies alles mit einem negativen Vorzeichen.

Das heißt, in menschlichen Worten, wir wählen die Kurse von 4 Währungen so aus, dass alle Währungspaare im Experiment Werte erhalten, die den Anfangswerten dieser Paare entsprechen. Mmm, lass uns das Rätsel lösen - in der Stirn!

Ergebnisse


Um mich nicht zu dehnen, werde ich Sie sofort über Folgendes informieren: Das gesamte Experiment war erfolgreich, der Code funktionierte, der Fehler ging nahe, nahe Null. Aber dann habe ich festgestellt, dass die Ergebnisse immer unterschiedlich sind.

Eine Frage für Kenner: Es scheint, dass diese Aufgabe eine unbegrenzte Anzahl von Lösungen hat, aber darin bin ich eine vollständige Null, ich denke, sie werden es mir in den Kommentaren sagen.

Um die (Un-) Stabilität der Lösung zu überprüfen, habe ich 1000 Mal simuliert, ohne den PRNG-Startwert für die Startwerte der Währungswerte festzulegen.

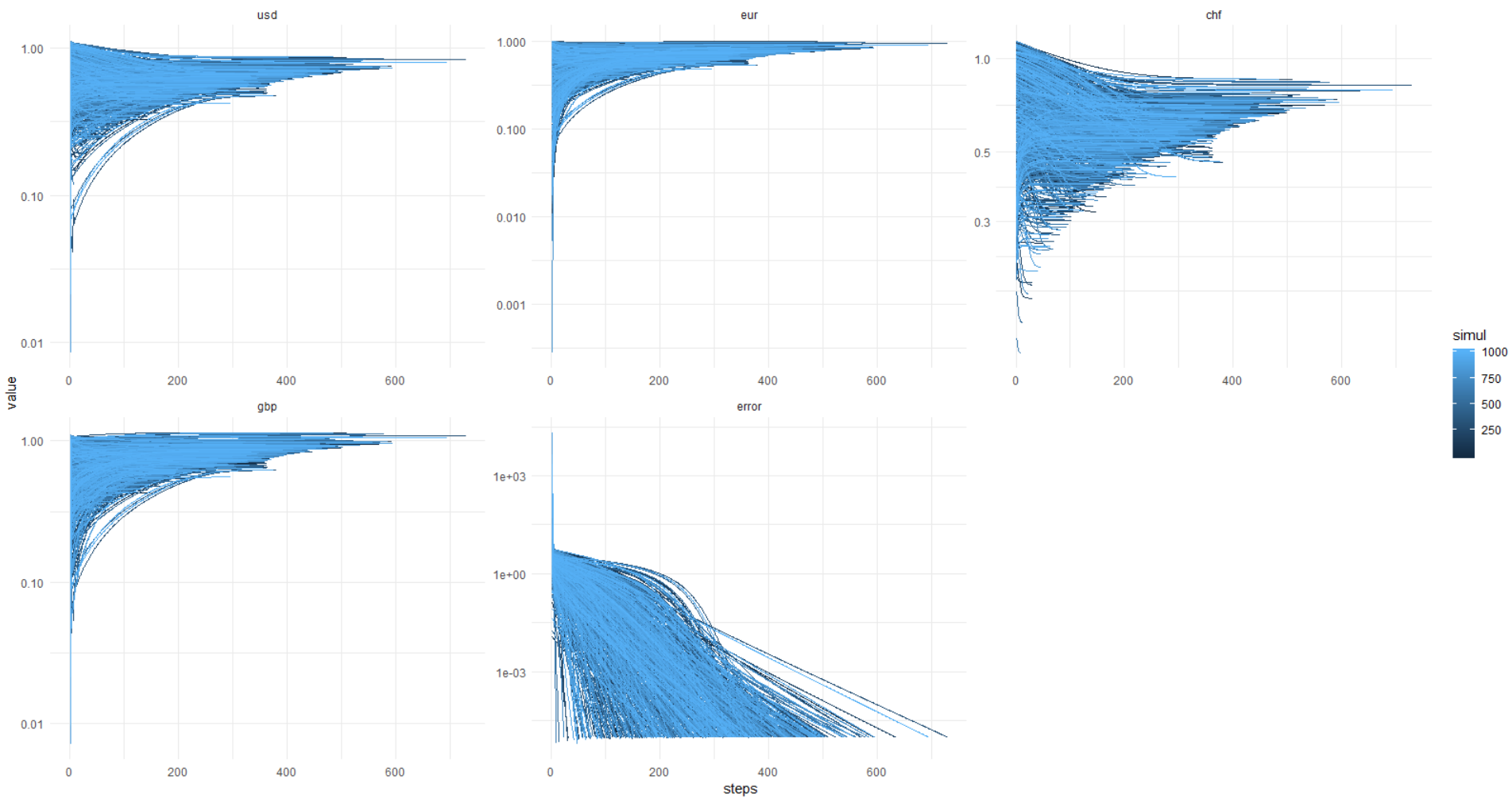
Und hier kommt das Bild aus der Kata: Der Fehler erreicht immer 0,00001 und weniger (die Optimierung wird auf diese Weise eingestellt), während die Werte der Währungen dem Teufel schweben, weiß wo. Es stellt sich heraus, dass es immer eine andere Entscheidung gibt, meine Herren!

Nochmals dieses Bild, y-Achse in den ursprünglichen Einheiten (nicht log.):



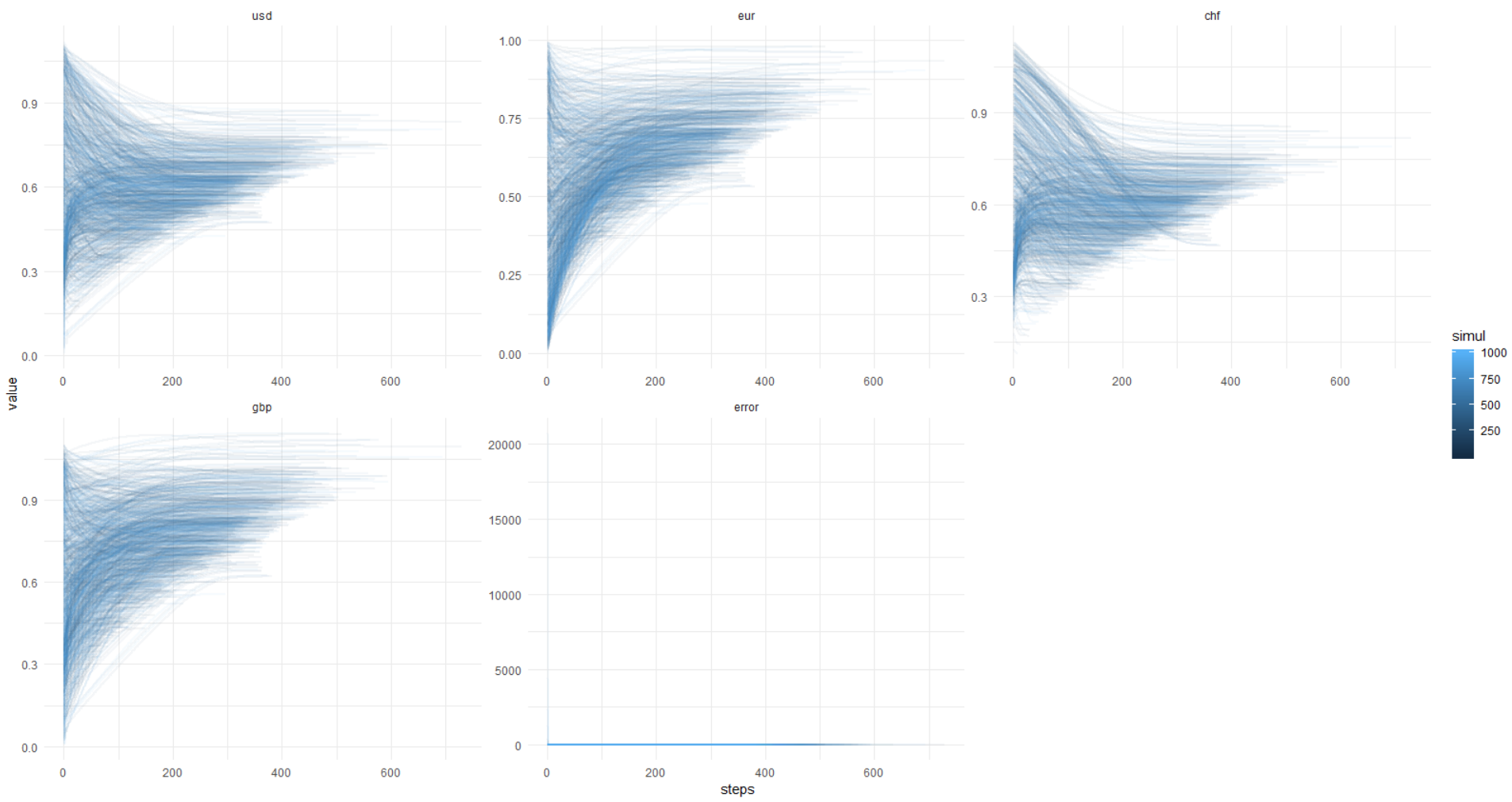
Damit Sie dies wiederholen können, füge ich unten den vollständigen Code hinzu.

Code
 # clear environment rm(list = ls()); gc() ## load libs library(data.table) library(ggplot2) library(magrittr) ## set WD -------------------------------- # your dir here ... ## set vars ------------- currs <- c( 'usd', 'eur', 'chf', 'gbp' ) ############ ## RUN SIMULATION LOOP ------------------------------- simuls <- 1000L simul_dt <- data.table() for( s in seq_len(simuls) ) { #set.seed(111) usd <- runif(1) eur <- runif(1) chf <- runif(1) gbp <- runif(1) # snapshot of values at time t eurusd <- 1.12012 gbpusd <- 1.30890 eurchf <- 1.14135 eurgbp <- 0.85570 gbpchf <- 1.33373 usdchf <- 1.01896 ## symbolic task ------------ express <- expression( (eurusd - eur / usd) ^ 2 + (gbpusd - gbp / usd) ^ 2 + (eurchf - eur / chf) ^ 2 + (eurgbp - eur / gbp) ^ 2 + (gbpchf - gbp / chf) ^ 2 + (usdchf - usd / chf) ^ 2 ) ## define gradient and iterate to make descent to zero -------------- iter_max <- 1e+3 lr <- 1e-3 min_tolerance <- 0.00001 rm(grad_desc_func) grad_desc_func <- function( lr, curr_list ) { derivs <- character(length(curr_list)) deriv_vals <- numeric(length(curr_list)) grads <- numeric(length(curr_list)) # symbolic derivatives derivs <- sapply( curr_list, function(x){ D(express, x) } ) # derivative values deriv_vals <- sapply( derivs, function(x){ eval(x) } ) # gradient change values -deriv_vals * lr } ## get gradient values ---------- progress_list <- list() for( i in seq_len(iter_max) ) { grad_deltas <- grad_desc_func(lr, curr_list = currs) currency_vals <- sapply( currs , function(x) { # update currency values current_val <- get(x, envir = .GlobalEnv) new_delta <- grad_deltas[x] if(new_delta > -1 & new_delta < 1) { new_delta = new_delta } else { new_delta = sign(new_delta) } new_val <- current_val + new_delta if(new_val > 0 & new_val < 2) { new_val = new_val } else { new_val = current_val } names(new_val) <- NULL # change values of currencies by gradient descent step in global env assign(x, new_val , envir = .GlobalEnv) # save history of values for later plotting new_val } ) progress_list[[i]] <- c( currency_vals, eval(express) ) if( eval(express) < min_tolerance ) { break('solution was found') } } ## check results ---------- # print( # paste0( # 'Final error: ' # , round(eval(express), 5) # ) # ) # # print( # round(unlist(mget(currs)), 5) # ) progress_dt <- rbindlist( lapply( progress_list , function(x) { as.data.frame(t(x)) } ) ) colnames(progress_dt)[length(colnames(progress_dt))] <- 'error' progress_dt[, steps := 1:nrow(progress_dt)] progress_dt_melt <- melt( progress_dt , id.vars = 'steps' , measure.vars = colnames(progress_dt)[colnames(progress_dt) != 'steps'] ) progress_dt_melt[, simul := s] simul_dt <- rbind( simul_dt , progress_dt_melt ) } ggplot(data = simul_dt) + facet_wrap(~ variable, scales = 'free') + geom_line( aes( x = steps , y = value , group = simul , color = simul ) ) + scale_y_log10() + theme_minimal()


Der Code für 1000 Simulationen funktioniert ungefähr eine Minute lang.

Fazit


Folgendes bleibt mir unklar:

  • Ist es möglich, die Lösung auf knifflige mathematische Weise zu stabilisieren?
  • ob es eine Konvergenz mit mehr Währungen und Währungspaaren geben wird;
  • Wenn es keine Stabilität geben kann, werden unsere Währungen für jeden neuen Datenschnappschuss so laufen, wie sie möchten, wenn Sie den PRNG-Startwert nicht reparieren, und dies ist ein Fehler.

Die ganze Idee scheint sehr vage zu sein, da keine verständlichen Voraussetzungen und Einschränkungen vorliegen. Aber es war interessant!

Nun, ich wollte auch sagen, dass Sie auf OLS verzichten können, wenn die Daten schwierig sind, die Matrizen singulär sind oder wenn die Theorie wenig bekannt ist (ehh ...).

Danke eavprog für die erste Nachricht.

Tschüss!

Source: https://habr.com/ru/post/de450874/

More articles:


All Articles