Vorwort

Neben meinem jüngsten Artikel möchte ich auch über das Thema MU ( M ulti U ser) MIMO sprechen. Ich habe bereits Professor Haardts einen sehr berühmten Artikel erwähnt , in dem er zusammen mit seinen Kollegen einen Algorithmus zur Trennung von Benutzern in einem Downlink (Downlink) vorschlägt, der auf linearen Methoden basiert, nämlich die Blockdiagonalisierung eines Kanals. Der Artikel hat eine beeindruckende Anzahl von Zitaten und ist auch der Eckpfeiler für eine der Prüfungsaufgaben. Warum also nicht die Grundlagen des vorgeschlagenen Algorithmus herausfinden?

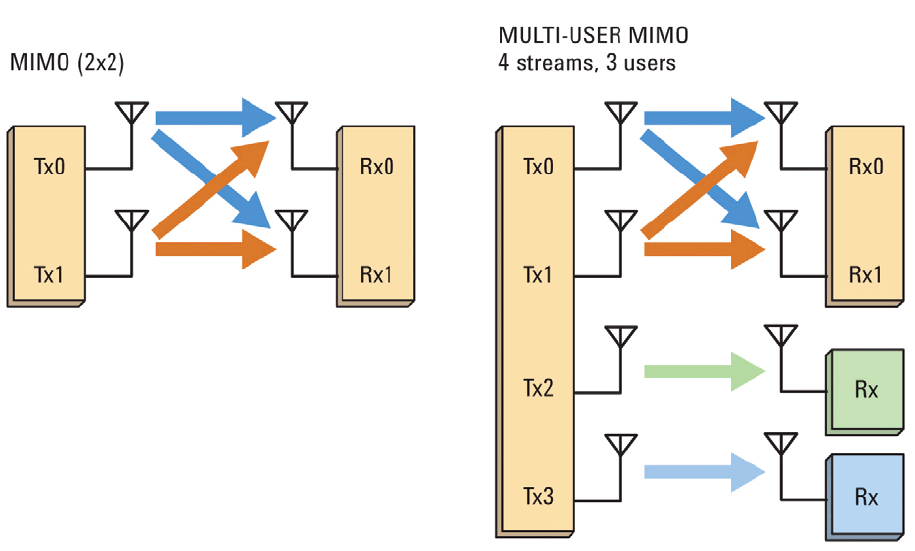
Erklärung des Problems

Lassen Sie uns zunächst entscheiden, in welchem Bereich des MIMO-Themas wir jetzt arbeiten werden.
Herkömmlicherweise können alle Übertragungsmethoden im Rahmen der MIMO-Technologie in zwei Hauptgruppen unterteilt werden:

Räumliche Vielfalt

Das Hauptziel besteht darin, die Störfestigkeit des Getriebes zu erhöhen. Wenn räumliche Kanäle vereinfacht werden, duplizieren sie sich gegenseitig, wodurch wir die beste Übertragungsqualität erhalten.

Beispiele:
- Blockcodes (zum Beispiel das Alamuti-Schema );
- Codes basierend auf dem Viterbi-Algorithmus.

Räumliches Multiplexen

Das Hauptziel ist die Erhöhung der Übertragungsgeschwindigkeit. Wir haben bereits in einem früheren Artikel besprochen, dass der MIMO-Kanal unter bestimmten Bedingungen als eine Reihe paralleler SISO-Kanäle betrachtet werden kann. Tatsächlich ist dies die zentrale Idee des räumlichen Multiplexens: die maximale Anzahl unabhängiger Informationsflüsse zu erreichen. Das Hauptproblem in diesem Fall ist die Unterdrückung von Inter-Channel-Interferenzen (Inter-Channel-Interferenzen) , für die es mehrere Klassen von Lösungen gibt:

- horizontale Kanaltrennung;
- vertikal (zum Beispiel der V-BLAST-Algorithmus);
- Diagonale (zum Beispiel der D-BLAST-Algorithmus).

Aber das ist natürlich nicht alles.

Die Idee des räumlichen Multiplexens kann erweitert werden: Nicht nur Kanäle, sondern auch Benutzer zu teilen (SDMA - Space Division Multiple Access).

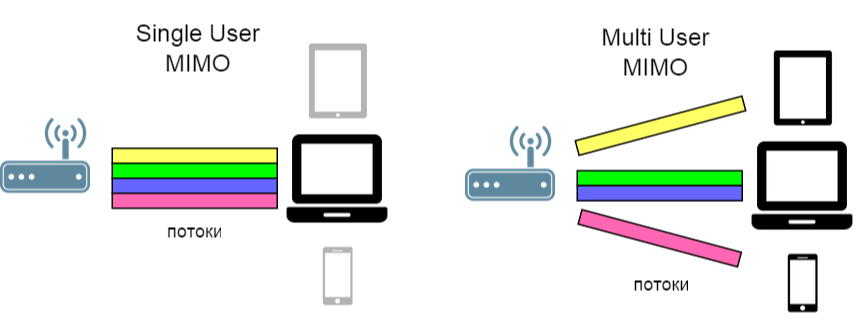
( Link zur Quelle der Illustration )

Folglich ist es in diesem Fall bereits erforderlich, gegen Interferenzen zwischen Benutzern zu kämpfen . Zu diesem Zweck wurde ein Algorithmus namens Blockdiagonalisierung Zero-Forcing vorgeschlagen , den wir heute betrachten.

Mathematische Beschreibung

Beginnen wir nach wie vor mit dem empfangenen Signalmodell. Genauer gesagt zeigen wir auf dem Diagramm, woher und was kommt:

Die Kanalmatrix hat in diesem Fall die Form:

$\ underset {M_R \ times M_T} {\ mathbf {H}} = \ begin {bmatrix} \ underset {M_ {R1} \ times M_T} {\ mathbf {H} _1} \\ \ underset {M_ {R2} \ mal M_T} {\ mathbf {H} _2} \\. \\. \\. \\ \ underset {M_ {RK} \ times M_T} {\ mathbf {H} _K} \ end {bmatrix} \ qquad (1)$

mit der Gesamtzahl der Sendeantennen M_T und die Gesamtzahl der Empfangsantennen $M_R = \ sum_ {k = 1} ^ K M_ {Rk}$ .

Wichtig :
Dieser Algorithmus kann nur angewendet werden, wenn die Anzahl der Sendeantennen größer oder gleich der Gesamtzahl der Empfangsantennen ist:
$M_R \ leq M_T$

Diese Bedingung wirkt sich direkt auf die Eigenschaften der Diagonalisierung aus.

Das Modell der empfangenen Symbole (Signale) kann also in Vektorform geschrieben werden als:

$\ mathbf {r} = \ mathbf {D} \ left (\ mathbf {H} \ mathbf {F} \ mathbf {s} + \ mathbf {n} \ right) \ qquad (2)$

Interessanter ist es jedoch, die Formel für einen bestimmten Benutzer zu betrachten:

$r_k = \ mathbf {D} _k \ left (\ mathbf {H} _k \ mathbf {F} _k s_k + \ mathbf {H} _k \ sum_ {i = 1, i \ neq k} ^ K \ mathbf {F} _i s_i + n_k \ right) \ qquad (3)$

In der Tat:

$\ mathbf {H} _k \ mathbf {F} _k s_k$ Ist ein nützliches Signal für den k-ten Benutzer,
$\ mathbf {H} _k \ sum_ {i = 1, i \ neq k} ^ K \ mathbf {F} _i s_i$ - Dies ist eine Störung durch andere Benutzer.

- additives Rauschen.

Wir kommen also zur Formulierung der Hauptaufgabe:

Sie können solche Matrizen finden $\ mathbf {F}$ so dass der Interferenzteil auf Null geht!

Das werden wir tun.

Beschreibung des Algorithmus

Wir werden die Beschreibung anhand eines Beispiels durchführen, und zur Veranschaulichung werde ich Screenshots aus erster Hand geben und sie ein wenig kommentieren.

Betrachten Sie den ersten Benutzer:

Lassen Sie uns über die Hauptschritte sprechen:

Wir machen eine Matrix $\ mathbf {\ hat {H} _1}$ von Kanalmatrizen aller anderen Benutzer.

Wir zerlegen es mit der SVD- Methode.
In der Matrix $\ mathbf {\ hat {V} _1}$ wir finden den Rauschunterraum (Null-Unterraum) - die Matrix $\ mathbf {\ hat {V} _1 ^ {(0)}$ (d. h. alles, was über den Rang der Matrix hinausgeht $\ mathbf {\ hat {H} _1}$ - bezeichne es )
Wir setzen aus dieser Rauschmatrix und ihrer hermitischen Konjugation eine Projektionsmatrix zusammen $\ mathbf {P_1}$ .

Gehen Sie voran:

Nun der ursprüngliche Teil der Kanalmatrix $\ mathbf {H} _1$ multiplizieren Sie mit der resultierenden Projektionsmatrix $\ mathbf {P} _1$ .
Wir zerlegen das Ergebnis durch SVD.
In der Matrix $\ mathbf {V_1} ^ H.$ wähle Linien wo - Rang $\ mathbf {H} _1 \ mathbf {P} _1$ .
Transponiere sie und erhalte die Matrix $\ mathbf {F} _1$ (oder $\ mathbf {M} _1$ - wo wie angegeben).

Daher wird dieser Vorgang für jeden Benutzer wiederholt. Ist das nicht die Magie der Mathematik: Mit den Methoden der linearen Algebra lösen wir vollständig technische Probleme!

Beachten Sie, dass in der Praxis nicht nur die erhaltenen Vorcodierungsmatrizen verwendet werden, sondern auch die Nachbearbeitungsmatrizen und die Matrix der Singularwerte (siehe Folien ). Letzteres zum Beispiel zum Ausgleich der Leistung nach dem bereits bekannten Wassergießalgorithmus .

Wir modellieren den Algorithmus

Ich denke, es wird nicht überflüssig sein, eine kleine Simulation durchzuführen, um das Ergebnis zu konsolidieren. Dazu verwenden wir Python 3, nämlich:

import numpy as np

für grundlegende Berechnungen und:

 import pandas as pd

um das Ergebnis anzuzeigen.

Um mich nicht zu häufen, werde ich die Quelle hier einfügen

 class ZeroForcingBD: def __init__(self, H, Mrs_arr): Mr, Mt = np.shape(H) self.Mr = Mr self.Mt = Mt self.H = H self.Mrs_arr = Mrs_arr def __routines(self, H, mr, shift): # used in self.process() - See example above for illustration # inputs: # H - the whole channel matrix # mr - number of receive antennas of the i-th user # shift - how much receive antennas were considered before # outputs: # Uidx, Sigmaidx, Vhidx - SVD decomposition of the H_iP_i # d - rank of the hat H_i # Hidx - H_i (channel matrix for the i-th user) # r - rank of the H_i Hidx = H[0+shift:mr+shift,:] # H_i (channel matrix for the i-th user) r = np.linalg.matrix_rank(Hidx) # rank of the H_i del_idx = [i for i in range(0+shift, mr+shift, 1)] # row indeces of H_i in H H_hat_idx = np.delete(H, del_idx, 0) # hat H_i d = np.linalg.matrix_rank(H_hat_idx) # rank of the hat H_i U, Sigma, Vh = np.linalg.svd(H_hat_idx) # SVD Vhn = Vh[d:, :] # null-subspace of V^H Vn = np.matrix(Vhn).H # null-subspace of V Pidx = np.dot(Vn, np.matrix(Vn).H) # projection matrix Uidx, Sigmaidx, Vhidx = np.linalg.svd(np.dot(Hidx, Pidx)) # SVD of H_iP_i return Uidx, Sigmaidx, Vhidx, d, Hidx, r def process(self): # used in self.obtain_matrices() # outputs: # F - whole filtering (pre-coding) matrix (array of arrays) # D - whole demodulator (post-processing) matrix (array of arrays) # H - the whole channel matrix (array of arrays) shift = 0 H = self.H F = [] D = [] Hs = [] for mr in self.Mrs_arr: Uidx, Sigmaidx, Vhidx, d, Hidx, r = self.__routines(H, mr, shift) Vhidx1 = Vhidx[:r,:] # signal subspace Fidx = np.matrix(Vhidx1).H F.append(Fidx) D.append(Uidx) Hs.append(Hidx) shift = shift + mr return F, D, Hs def obtain_matrices(self): # used to obtain pre-coding and post-processing matrices # outputs: # FF - whole filtering (pre-coding) matrix # DD - whole demodulator (post-processing) matrix (array of arrays) F, D, Hs = self.process() FF = np.hstack(F) # Home Task: calculation of the demodulator matrices :) return FF

Angenommen, wir haben 8 Sendeantennen und 3 Benutzer mit 3, 2 und 3 Empfangsantennen:

 Mrs_arr = [3,2,3] # 1st user have 3 receive antennas, 2nd user - 2 receive antennas, 3d user - 3 receive antennas Mr = sum(Mrs_arr) # total number of the receive antennas Mt = 8 # total number of the transmitt antennas H = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2); #Rayleigh flat faded channel matrix (MrxMt)

Wir initialisieren unsere Klasse und wenden die entsprechenden Methoden an:

 BD = ZeroForcingBD(H, Mrs_arr) F, D, Hs = BD.process() FF = BD.obtain_matrices()

Wir bringen zu einer lesbaren Form:

 df = pd.DataFrame(np.dot(H, FF)) df[abs(df).lt(1e-14)] = 0

Und lassen Sie uns aus Gründen der Klarheit ein wenig heben (obwohl Sie darauf verzichten können):

 print(pd.DataFrame(np.round(np.real(df),100)))

Sie sollten so etwas bekommen:

Eigentlich sind sie hier Blöcke, hier ist es und Diagonalisierung. Und Minimierung von Störungen.

Solche Dinge.

Literatur

Spencer, Quentin H., A. Lee Swindlehurst und Martin Haardt. "Zero-Forcing-Methoden für das räumliche Downlink-Multiplexing in Mehrbenutzer-MIMO-Kanälen." IEEE-Transaktionen zur Signalverarbeitung 52.2 (2004): 461-471.
Martin Haard " Robuste Übertragungsverarbeitung für Mehrbenutzer-MIMO-Systeme "

Dem Lehrpersonal und der Studentengemeinschaft meines Heimatberufs sage ich Hallo!

MU-MIMO: einer der Implementierungsalgorithmen