Zufällige Permutationen und zufällige Partitionen

Seit vielen Jahren gebe ich Kurse in Kombinatorik und Grafik für Studenten der Mathematik und Informatik (wie ist es auf Russisch, Informatiker?), Zuvor an der Akademischen Universität und jetzt an der St. Petersburg State University . Unser Programm ist so konzipiert, dass diese Themen als Teil der „theoretischen Informatik“ behandelt werden (andere Themen sind Algorithmen, Komplexität, Sprachen und Grammatiken). Ich kann nicht sagen, wie metaphysisch oder historisch gerechtfertigt: Dennoch wurden kombinatorische Objekte (Graphen, Mengen-Systeme, Permutationen, karierte Figuren usw.) lange vor dem Aufkommen von Computern untersucht, und jetzt ist letzteres, obwohl wichtig, bei weitem nicht der einzige Grund für Interesse ihn. Aber wenn man sich die Spezialisten für Kombinatorik und theoretische Informatik ansieht, sind es überraschenderweise oft dieselben Leute: Lovas, Alon, Semeredi, Razborov und darüber hinaus. Dafür gibt es wahrscheinlich Gründe. In meinem Unterricht bieten olympische Programmiermeister oft sehr nicht triviale Lösungen für komplexe Probleme an (ich werde sie nicht auflisten, jeder, der neugierig auf die Top-Codeforces ist). Im Allgemeinen denke ich, dass einige Dinge aus der Kombinatorik für die Community von Interesse sein können. Sprechen Sie, ob etwas so ist oder nicht.

Sie müssen eine zufällige Permutation von Zahlen von 1 bis erstellen$$ $ inline $ n $ inline $ so dass alle Permutationen gleich wahrscheinlich sind. Dies kann auf viele Arten geschehen: Wählen Sie beispielsweise zuerst zufällig das erste Element aus, dann aus der verbleibenden Sekunde und so weiter. Oder Sie können etwas anderes tun: Punkte zufällig auswählen$$ $ inline $ t_1, t_2, \ ldots, t_n $ inline $ im Segment$$ $ inline $ [0,1] $ inline $ und sehen, wie sie bestellt werden. Wenn Sie die kleinste der Zahlen durch 1, die zweite durch 2 usw. ersetzen, erhalten Sie eine zufällige Permutation. Leicht zu sehen, dass alles$$ $ inline $ n! $ inline $ Permutationen sind ebenso wahrscheinlich. Es ist möglich und nicht im Segment$$ $ inline $ 0.1 $ inline $ Wählen Sie Punkte und zum Beispiel zwischen Zahlen von 1 bis$$ $ inline $ n $ inline $ . Hier sind Zufälle möglich (für ein Segment sind sie auch möglich, aber mit einer Wahrscheinlichkeit von Null, sodass sie uns nicht stören) - Sie können auf unterschiedliche Weise damit umgehen, z. B. indem Sie die übereinstimmenden Zahlen zusätzlich neu anordnen. Oder nimm N größer, damit die Wahrscheinlichkeit eines Zufalls gering ist (der Fall, wenn$$ $ inline $ N = 365 $ inline $ und$$ $ inline $ n $ inline $ Es gibt die Anzahl der Schüler in Ihrer Klasse, und wir sprechen über das Zusammentreffen von zwei Geburtstagen.) Eine Variation dieser Methode: zufällig notieren$$ $ inline $ n $ inline $ Punkte in einem Einheitsquadrat und sehen, wie ihre Ordinaten relativ zu Abszissen geordnet sind. Eine weitere Variante: Markieren Sie im Segment$$ $ inline $ n-1 $ inline $ Zeigen Sie und sehen Sie, wie die Längen der Segmente, in die es unterteilt ist, geordnet sind. Der entscheidende Punkt bei diesen Ansätzen ist die Unabhängigkeit der Tests, nach deren Ergebnissen eine zufällige Umlagerung aufgebaut wird. Andrei Nikolaevich Kolmogorov sagte, dass die Wahrscheinlichkeitstheorie eine Theorie des Maßes plus Unabhängigkeit ist - und dies wird von jedem bestätigt, der sich mit Wahrscheinlichkeit befasst hat.

Ich werde am Beispiel der Hakenformel für Bäume zeigen, wie dies hilft:



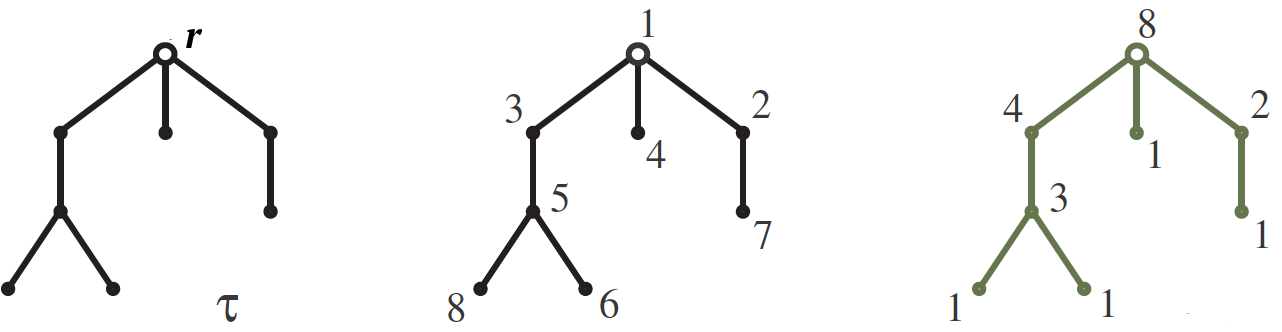
Lass$$ $ inline $ \ tau $ inline $ - an der Wurzel aufgehängt$$ $ inline $ r $ inline $ Baum mit$$ $ inline $ n $ inline $ Spitzen wachsen nach unten wie auf dem Bild. Unser Ziel ist es, die Anzahl zu berechnen$$ $ inline $ S (\ tau) $ inline $ Nummerierung der Baumkronen$$ $ inline $ \ tau $ inline $ Zahlen von 1 bis$$ $ inline $ n $ inline $ so dass für jede Kante die Zahl an ihrer Oberseite größer ist als an der Unterseite. Eine dieser Zahlen ist im mittleren Bild dargestellt. Die Antwort wird unter Verwendung von Hakengrößen formuliert. Haken$$ $ inline $ H (v) $ inline $ Spitzen$$ $ inline $ v $ inline $ Nennen wir einen Teilbaum, der aus diesem Scheitelpunkt wächst, und seine Größe ist einfach die Anzahl der Scheitelpunkte darin. Die Hakenlängen sind im rechten Bild neben den entsprechenden Eckpunkten angegeben. Die Anzahl der Zahlen ist also$$ $ inline $ n! $ inline $ geteilt durch das Produkt der Hakengrößen, also für unser Beispiel

$$$$ display $$ S (\ tau) = \, \ frac {8!} {8 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 \ cdot 1 \ cdot 1 \ cdot 1} = 210. $$ display $ $

Wir können diese Formel auf verschiedene Weise beweisen, beispielsweise durch Induktion der Anzahl der Eckpunkte, aber unsere Sicht auf zufällige Permutationen ermöglicht es uns, den Beweis ohne Berechnungen durchzuführen. Es ist nicht nur durch Eleganz besser, sondern auch durch die Tatsache, dass es sich gut auf subtilere Fragen zur Nummerierung mit den vorgeschriebenen Ungleichungen verallgemeinert, aber nicht darüber jetzt. Nehmen Sie also n verschiedene reelle Zahlen und platzieren Sie sie zufällig oben auf dem Baum, jede mit einer Zahl, alle$$ $ inline $ n! $ inline $ Permutationen sind ebenso wahrscheinlich. Wie groß ist die Wahrscheinlichkeit, dass für jede Kante die Zahl am oberen Scheitelpunkt der Kante größer ist als die Zahl am unteren Scheitelpunkt? Die Antwort lautet:$$ $ inline $ S (\ tau) / n! $ inline $ und es hängt nicht von einer Reihe von Zahlen ab. Und wenn es nicht darauf ankommt, betrachten wir die Zahlen auch zufällig ausgewählt - für die Bestimmtheit im Intervall$$ $ inline $ [0,1] $ inline $ . Anstatt zuerst zufällig Zahlen auszuwählen und sie dann zufällig oben im Baum anzuordnen, können wir einfach zufällig und unabhängig eine Zahl an jedem Scheitelpunkt auswählen: Ihre Neuanordnung erfolgt automatisch zufällig. Auf diese Weise,$$ $ inline $ S (\ tau) / n! $ inline $ Dies ist die Wahrscheinlichkeit, dass für zufällige unabhängige Zahlen$$ $ inline $ \ xi (v) $ inline $ für jeden Scheitelpunkt einen ausgewählt$$ $ inline $ v $ inline $ Holz$$ $ inline $ \ tau $ inline $ , alle Ungleichungen der Form$$ $ inline $ \ xi (v)> \ xi (u) $ inline $ für alle Kanten$$ $ inline $ v \ bis u $ inline $ ,$$ $ inline $ v $ inline $ Ist der obere Scheitelpunkt der Rippe und$$ $ inline $ u $ inline $ - unten. Wir formulieren diese Bedingungen in einer äquivalenten Form, jedoch auf etwas andere Weise: für jeden Scheitelpunkt$$ $ inline $ v $ inline $ Ein solches Ereignis sollte eintreten - ich werde es benennen

$$$ inline $ Q (v) $ inline $ : Nummer$$ $ inline $ \ xi (v) $ inline $ - das Maximum unter allen Zahlen an den Eckpunkten des Hook-Teilbaums$$ $ inline $ H (v) $ inline $ .

Beachten Sie das$$ $ inline $ \ frac {1} {| H (v) |} $ inline $ Dies ist die Wahrscheinlichkeit eines Ereignisses$$ $ inline $ Q (v) $ inline $ . In der Tat im Haken$$ $ inline $ H (v) $ inline $ ist verfügbar$$ $ inline $ | H (v) | $ inline $ Scheitelpunkte und die maximale Hook-Nummer werden mit gleicher Wahrscheinlichkeit auf jeden von ihnen abgebildet$$ $ inline $ \ frac {1} {| H (v) |} $ inline $ . Also die Hakenformel$$ $ inline $ S (\ tau) / n! = \ prod_v \ frac {1} {| H (v) |} $ inline $ kann wie folgt formuliert werden: Die Wahrscheinlichkeit, dass alle Ereignisse gleichzeitig auftreten$$ $ inline $ Q (v) $ inline $ ist gleich dem Produkt der Wahrscheinlichkeiten dieser Ereignisse. Die Gründe dafür mögen vielfältig sein, aber der erste, der mir in den Sinn kommt, funktioniert hier: Diese Ereignisse sind unabhängig. Um dies zu verstehen, schauen wir uns zum Beispiel eine Veranstaltung an$$ $ inline $ Q (r) $ inline $ (entsprechend der Wurzel). Es besteht in der Tatsache, dass die Zahl in der Wurzel größer ist als alle anderen Zahlen in den Eckpunkten, und andere Ereignisse sich auf Vergleiche untereinander von Zahlen beziehen, die nicht in die Wurzel geschrieben sind. Also$$ $ inline $ Q (r) $ inline $ bezüglich der Nummer$$ $ inline $ \ xi (r) $ inline $ und Sätze von Zahlen an anderen Eckpunkten, und alle anderen Ereignisse liegen in der Reihenfolge der Zahlen an anderen Eckpunkten als der Wurzel. Wie wir bereits besprochen haben, sind "Ordnung" und "Menge" unabhängig, daher das Ereignis$$ $ inline $ Q (r) $ inline $ unabhängig von anderen. Wenn wir den Baum hinuntergehen, stellen wir fest, dass all diese Ereignisse unabhängig sind, von wo die erforderlichen folgen.

Normalerweise ist die Formel für Hooks die Formel für die Nummerierung nicht der Eckpunkte im Baum, sondern der Zellen im Young-Diagramm in Richtung der Koordinatenachsen zunehmen, und die Haken dort sind eher wie Haken als für Bäume. Diese Formel hat sich jedoch als komplizierter erwiesen und verdient einen gesonderten Beitrag.

Da ich es übrigens hatte, kann ich nicht anders, als über das Modell eines zufälligen Young-Diagramms zu sprechen. Junges Diagramm ist eine solche Figur aus$$ $ inline $ n $ inline $ Einheitsquadrate, die Länge der Zeilen nimmt von unten nach oben und die Länge der Spalten von links nach rechts zu. Anzahl der Young's Area Charts$$ $ inline $ n $ inline $ wird angezeigt$$ $ inline $ p (n) $ inline $ Diese wichtige Funktion verhält sich auf interessante und ungewöhnliche Weise: Sie wächst beispielsweise schneller als jedes Polynom, aber langsamer als jeder Exponent. Generieren Sie daher insbesondere ein zufälliges Young-Diagramm (wenn wir alle Flächendiagramme wollen$$ $ inline $ n $ inline $ waren gleich wahrscheinlich$$ $ inline $ 1 / p (n) $ inline $ ) ist keine triviale Angelegenheit. Wenn Sie beispielsweise nacheinander Zellen hinzufügen und einen Ort zum zufälligen Hinzufügen auswählen, haben verschiedene Diagramme unterschiedliche Wahrscheinlichkeiten (die Wahrscheinlichkeit eines einzeiligen Diagramms ist also gleich$$ $ inline $ 1/2 ^ {n-1} $ inline $ .) Es stellt sich als unterhaltsames Maß in den Diagrammen heraus, aber nicht einheitlich. Uniform kann wie folgt erhalten werden. Nimm die Nummer$$ $ inline $ t \ in (0,1) $ inline $ Für unsere Zwecke sind die Zahlen in der Region am besten geeignet$$ $ inline $ 1- \ mathrm {const} / \ sqrt {n} $ inline $ . Für jeden$$ $ inline $ k = 1,2, \ ldots $ inline $
Betrachten Sie die geometrische Verteilung auf nicht negativen ganzen Zahlen mit Mittelwert$$ $ inline $ t ^ k $ inline $ (d. h. Wahrscheinlichkeit der Zahl$$ $ inline $ m = 0,1, \ ldots $ inline $ ist gleich$$ $ inline $ t ^ {km} (1-t ^ k) $ inline $ ) Wir wählen danach eine Zufallsvariable$$ $ inline $ m_k $ inline $ (Es gibt viele Möglichkeiten, dies zu organisieren). Auf freiem Fuß$$ $ inline $ k $ inline $ höchstwahrscheinlich 0. Schauen wir uns das Young-Diagramm an, in dem$$ $ inline $ m_k $ inline $ Zeilen sind Länge$$ $ inline $ k $ inline $ bei jedem$$ $ inline $ k = 1,2, \ ldots $ inline $ . Ich nenne es die Schiffsmethode, weil die Gesamtfläche manchmal gleich ist$$ $ inline $ n $ inline $ . Wenn nicht gleich, wiederholen Sie das Experiment. Eigentlich gleich$$ $ inline $ n $ inline $ sie oft genug, wenn sie klug wählt$$ $ inline $ t \ in (0,1) $ inline $ . Ich lade den Leser ein, unabhängig zu beweisen, dass alle Diagramme eines bestimmten Bereichs gleich wahrscheinlich sind, und die Anzahl der Schritte zu schätzen.