29. März 2019 - Michael Trott, Hauptforscher
Eintrag
In der sogenannten „neuen SI“ - einer
aktualisierten Version des Internationalen Einheitensystems , die sieben grundlegende Maßeinheiten (Sekunde, Meter, Kilogramm, Ampere, Kelvin, Maulwurf und Candela) festlegt und am 20. Mai 2019 in Kraft tritt - werden alle SI-Einheiten in Kraft treten bestimmt durch die genauen Werte der physikalischen Grundkonstanten. Infolgedessen werden alle oben genannten SI-Einheiten (Newton, Volt, Ohm, Pascal usw.) letztendlich als Grundkonstanten ausgedrückt. (Schließlich wird die Grundlagenphysik unser tägliches Leben buchstäblich kontrollieren ☺)
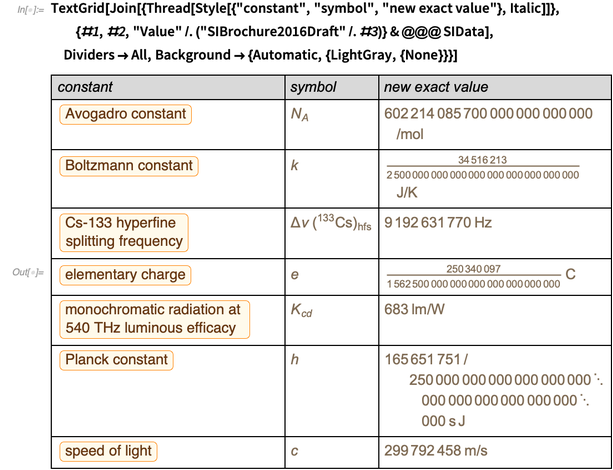
Die folgende Tabelle zeigt, wie sich alles von Montagabend, dem 20. Mai, bis Dienstagmorgen, dem 21. Mai dieses Jahres ändern wird.
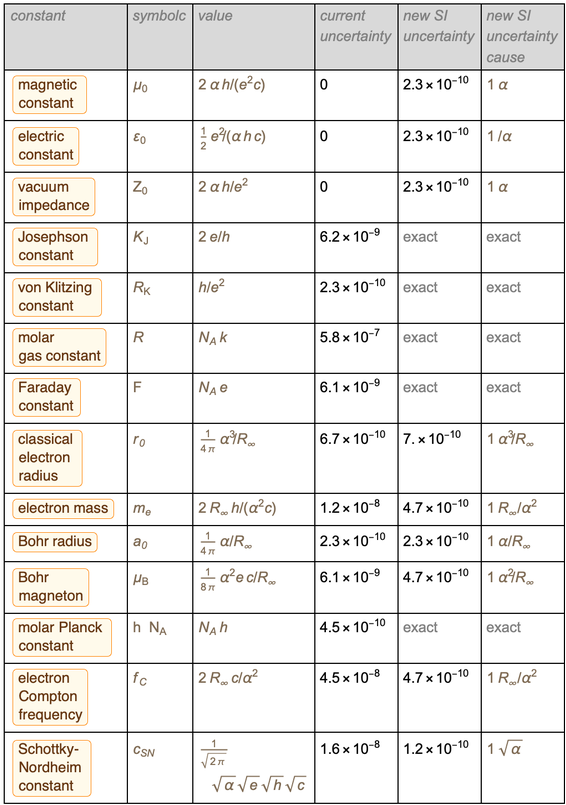
Das Berechnen von Daten aus dieser Tabelle ist das Ziel dieses Blogs. Beginnen wir also mit einem kurzen Überblick darüber, was sich in der neuen SI ändern wird.
Neben dem bekannten exakten Wert der Lichtgeschwindigkeit haben in vier Wochen weitere vier physikalische Konstanten - die Planck-Konstante, die Boltzmann-Konstante, die Avogadro-Konstante und die Millikan-Konstante (oft als elementare elektrische Ladung bezeichnet) - exakte Werte. Die Entscheidung über diese Änderung wurde im November letzten Jahres international getroffen (darüber habe ich in meinem letzten geschrieben
Blog).
Unten finden Sie einen Ausschnitt aus Seite 12 des aktuellen Entwurfs der
SI-Broschüre .
Beachten Sie, dass in diesen Definitionen Dezimalzahlen als exakte Dezimalzahlen gemeint sind, nicht beispielsweise Maschinennummern auf einem Computer, die eine endliche Genauigkeit haben und keine exakten Zahlen sind. Die Übergangsfrequenz in der gespaltenen Feinstruktur von Cs-133, die Lichtgeschwindigkeit und die "Lichtausbeute" haben bereits heute genaue Werte.
Die Welt diskutiert zukünftige Veränderungen
Diese Änderung wird einige interessante Konsequenzen für andere physikalische Konstanten haben: Einige Konstanten, die derzeit gemessen werden und Fehler aufweisen, werden genau, und einige Konstanten, die derzeit genau sind, werden in Zukunft ungefähre Werte mit endlichen Fehlern haben . Diese Änderungen sind unvermeidlich, um die Gesamtsystemkonsistenz zu gewährleisten.
Die diesjährige erste Ausgabe
von Physics of the World ging auf dieses Thema in einem
Brief an den Herausgeber von William Hough ein. er schrieb:
Mit der Ladungsfixierung auf dem Elektron ( e ) und der Planckschen Konstante ( h ) sind jetzt alle physikalischen Einheiten „in Stein verewigt“, was sehr schön ist. Aber das wirft eine unangenehme Frage auf. Feinstrukturkonstante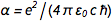 
wobei c die Lichtgeschwindigkeit ist und 
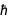Das 
. Aus bekannten Gleichungen 
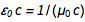und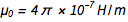 
das finden wir schnell 
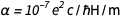. Dies ist natürlich eine reine Zahl mit einer dimensionslosen Größe, und sie ist jetzt für immer auf 1 / 137.13601 festgelegt, was sehr nahe am akzeptierten Wert liegt. Dies ist nicht überraschend, da der letztere Wert in den vereinbarten neuen Werten für e und ℏ verwendet würde . Aber die Natur hat ihren eigenen, uns derzeit unbekannten Wert, der deshalb in Diamant verewigt ist. Man kann uns verzeihen, dass wir es besser wissen als die Natur. Was aber, wenn die zukünftige Theorie des Universums akzeptiert wird und die genaue Bedeutung gibt? 
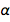Was unterscheidet sich wesentlich vom akzeptierten Wert? Könnte das passieren? Es gab Versuche, einen theoretischen Wert für α zu finden , aber sie umfassen bedrohliche und kontroverse Quantenelektrodynamik.
Das Problem ist, dass im neuen SI-System beide
und
wird jetzt mit einem Fehler ungenaue Werte haben. In diesem Blog werden wir die Wolfram-Sprache und ihr Wissen über physikalische Einheiten und Konstanten verwenden, um zu sehen, wie diese und andere physikalische Konstanten Fehler gewinnen (oder verlieren) und warum dies eine mathematische Konsequenz der Definition von Grundeinheiten ist.
Ein kurzer Überblick über die verwandten Inhaltsstoffe der Wolfram-Sprache
Wolfram Language ist ein einzigartiges Medium für numerische Experimente und symbolische Berechnungen, um mögliche Konsequenzen zu identifizieren. Neben den allgemeinen Rechenfunktionen sind hier drei Systemkomponenten sehr nützlich:
1) Wolfram Spracheinheiten und Struktur der physikalischen Größen.
Klassische Einheiten (wie Meter, Fuß usw.) können für Berechnungen und Visualisierungen verwendet werden. Und natürlich bei der Umrechnung von Maßeinheiten.
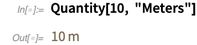
Die Umrechnung in gewöhnliche US-Einheiten ergibt aufgrund der genau definierten Verhältnisse der beiden Einheiten einen Bruchteil (und nicht einen ungefähren Wert der reellen Zahl!).
Physiker verwenden (besonders) gerne "natürliche" Einheiten. Oft sind diese natürlichen Einheiten einfach physikalische Konstanten oder Kombinationen davon. Zum Beispiel die Lichtgeschwindigkeit (hier wird die Eingabe in natürlicher Sprache verwendet).
In SI-Einheiten ausgedrückt (da dies Geschwindigkeit ist und Einheiten in Metern und Sekunden erforderlich sind) hat die Lichtgeschwindigkeit einen genauen Wert.
Andererseits hat die Planck-Konstante derzeit keinen genauen Wert. Somit ist sein Wert, ausgedrückt in SI-Basiseinheiten, eine ungefähre Dezimalzahl.
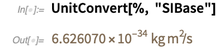
Bitte beachten Sie, dass die Genauigkeit von 6.626070 ... die Anzahl der bekannten Zahlen widerspiegelt.
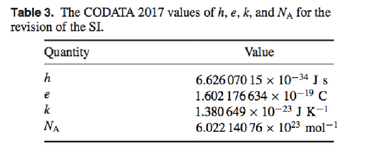
Dies ist der letzte empfohlene Wert für die Planck-Konstante, der in
CODATA 2017 zur Vorbereitung der Verfeinerung von Konstanten veröffentlicht wurde. Unten ist die entsprechende Tabelle:
Physikalische Konstanten (oder Kombinationen davon), die zwei physikalische Größen verbinden, können häufig als natürliche Einheiten verwendet werden. Die einfachsten Beispiele wären die Messung der Geschwindigkeit in Bezug auf die Lichtgeschwindigkeit oder das mikroskopische Drehmoment in Bezug auf
ℏ . Oder Energie kann als Masse mit einem impliziten Faktor gemessen werden
. Mit der Funktion
DimensionalCombinations können Sie nach Kombinationen physikalischer Konstanten suchen, mit denen Sie zwei bestimmte physikalische Größen in Beziehung setzen können. Beispielsweise können die folgenden Beziehungen zwischen Masse und Energie aufgebaut werden:
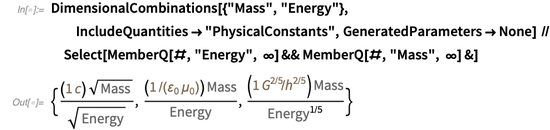
Die erste Gleichheit spiegelt Einsteins berühmte Formel wider
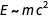
, die zweite ist das Äquivalent der ersten Beziehung, und die dritte - (dimensional) besagt, dass
.
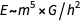
2) Die Entitätsklasse "
PhysicalConstant " wurde kürzlich zur
Wolfram Knowledgebase hinzugefügt.
Funktionen und Objekte in der Wolfram-Sprache werden „rechnerisch geboren“, dh sie sind für den Computer bereit. Aber um die reale Welt zu beschreiben und zu simulieren, benötigen Sie Daten über die reale Welt. Die Entitätsstruktur ist eine bequeme und vollständig integrierte Methode, um solche Daten zu erhalten. Nachfolgend einige Daten zu Elektron, Proton und Neutron.
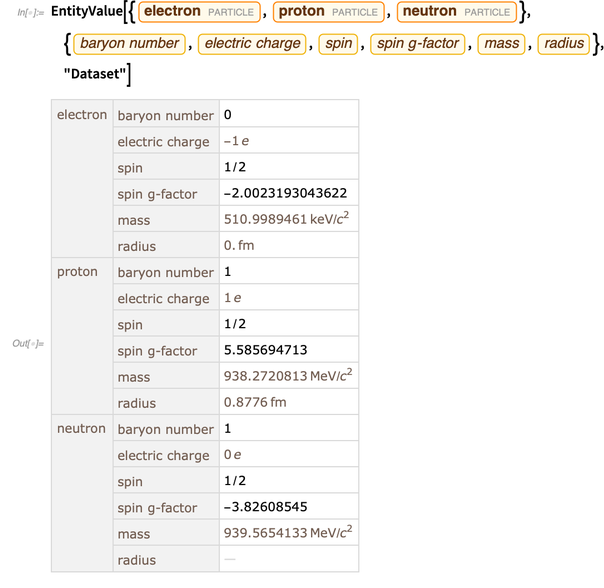
Eine der neuen Entitätseinheiten sind physikalische Konstanten. Derzeit enthält die Knowledge Base mehr als 250 physikalische Konstanten.
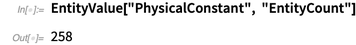
Unten finden Sie ein Dutzend zufällig ausgewählte Beispiele. Darüber hinaus enthält die Liste ohne eine klare Definition der Konstanten physikalische Konstanten, Massen grundlegender Teilchen, Lagrange-Parameter des Standardmodells usw. der Einfachheit halber auch
astronomische Konstanten gemäß dem astronomischen Almanach.
Die meisten grundlegenden physikalischen Konstanten wurden in der berühmten
Arbeit von Jean-Marc Levy-Leblond als Konstanten der Klasse C bezeichnet. Das Folgende sind Konstanten der Klassen C und B.
Nehmen Sie zum Beispiel die natürliche Zeiteinheit Planck-Zeit. Die
Funktionen ToEntity und
FromEntity erleichtern das Hin- und Herwechseln zwischen physischen Konstanten als Einheiten und physischen Konstanten als Entitäten. Eine Entität, die einer Planck-Zeiteinheit entspricht, wird unten gezeigt.
Die Wissensdatenbank enthält viele Metainformationen über ihn, beispielsweise die Werte in den neuesten CODATA-Listen.
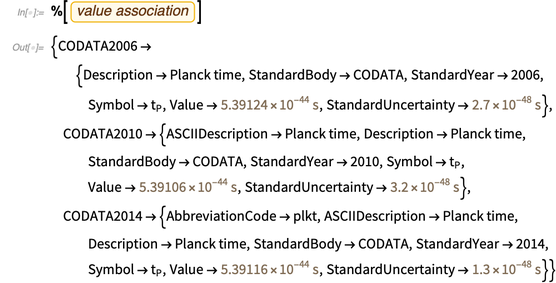
Die letzte Schlussfolgerung, die Bedeutung und Fehler enthält, führt uns zu der dritten wichtigen Funktion, die später nützlich sein wird:
3) Einführung der
Around [] -Funktion in Version 12 der Wolfram-Sprache. Die Funktion
Around [] liefert einen ungenauen Wert, der den Durchschnittswert und den Fehler angibt. Das arithmetische Modell
Around [] basiert auf dem
GUM (Leitfaden zum Ausdrücken von Messfehlern) - nicht zu verwechseln mit dem Leibniz Plus-Minus-Kalkül. Hier ist ein solcher Wert mit einem Fehler.
Der wichtigste und nützlichste Aspekt beim Rechnen mit fehlerhaften Werten ist, dass sie Korrelationen berücksichtigen. Die naive Verwendung solcher Werte in arithmetischen Zahlen oder Intervallen kann den resultierenden Fehler unterschätzen oder überschätzen.
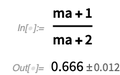
Unten sehen wir, dass die
AroundReplace [] -Funktion die Korrelation berücksichtigt.
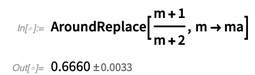
Zurück zum Brief an den Herausgeber
Verwenden wir nun diese drei Komponenten und den detaillierteren Brief von William Hough an den Herausgeber.
Bei den aktuellen Näherungswerten für
e und
ℏ sind diese beiden Werte für die Feinstrukturkonstante innerhalb der Grenzen ihrer Fehler konsistent. Der erste ist der Ausdruck aus dem Brief an den Herausgeber, und der zweite ist die Menge (
Menge []), die die Feinstrukturkonstante darstellt.
Alle paar Jahre veröffentlicht CODATA offizielle Werte der Grundkonstanten (siehe
Feinstrukturkonstanten ); Wie gesagt, die in der Wolfram-Sprache verwendeten Werte sind die neuesten CODATA-Werte, und der endgültige Fehler spiegelt sich in der Genauigkeit der Zahl wider.
Bitte beachten Sie, dass die direkt gemessene Feinstrukturkonstante etwas genauer ist als diejenige, die die Feinstrukturkonstante durch andere Konstanten ausdrückt.
Wenn wir die bevorstehenden exakten Werte von
e und
ℏ verwenden und den aktuellen exakten Wert verwenden
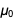
erhalten wir den folgenden exakten Wert für die Feinstrukturkonstante in der Form
.
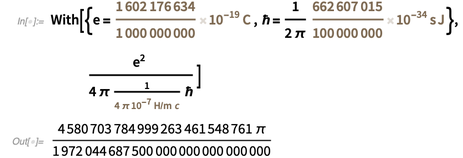
Es ist unwahrscheinlich, dass der Herr, der nicht einmal
Würfel spielt , eine solche Zahl für den Wert wählt
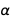
in unserem Universum. Dies bedeutet, dass während
e und
ℏ im neuen SI festgelegt sind, die aktuellen exakten Werte
und
muss zwangsläufig „entkoppelt“ werden (siehe auch Goldfarbs
Artikel zur Menge
neue SI). (Wir werden auf das Warum zurückkommen
und
bald ungenau werden.)
Dies bedeutet, dass diese Ergebnisse nach dem 20. Mai dieses Jahres von den unten angegebenen abweichen werden.
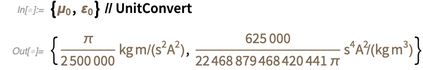
(In einer kurzen Anmerkung enthält die Entitätsklasse "
PhysicalConstant " auch geschätzte Werte für Konstanten, z. B. die Feinstrukturkonstante.)
Abgesehen von der theologischen Auseinandersetzung über die genaue Form der Feinstrukturkonstante, aus physikalischer Sicht, warum
und
sollte ungenau sein? Betrachten wir als Argument der Wahrscheinlichkeit
. Eines der herausragendsten Ergebnisse ist das Coulombsche Gesetz.
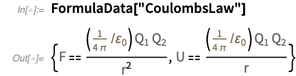
Im
bestehenden SI-System haben Ampere eine „genaue“ Definition:
Ein Ampere ist der Gleichstrom, der, wenn er in zwei parallelen Leitern unendlicher Länge mit einem leichten runden Querschnitt getragen und in einem Abstand von 1 Meter im Vakuum angeordnet wird, eine Kraft zwischen diesen Leitern erzeugt, die gleich ist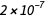 
Newton pro Meter Länge. Diese Definition verwendet rein mechanische Größen Newton und Meter (dh nach der Expansion ist dies eine Sekunde, Meter und Kilogramm). Es besteht keine Beziehung zur Ladung des Elektrons, und im bestehenden SI-System ist die Elementarladung eine experimentell gemessene Größe.
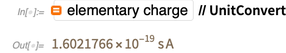
Und dieser experimentell gemessene Wert hat sich im Laufe der Jahre geändert und ist genauer geworden.
Die Kraft auf der linken Seite des Coulomb-Gesetzes (ausgedrückt in Newton) enthält die Grundeinheit des Kilogramms, die, nachdem der Wert der Planck-Konstante konstant geworden ist, ebenfalls genau definierbar wird. Da es keinen Grund zu der Annahme gibt, dass alle Naturgesetze in endlichen rationalen Zahlen ausgedrückt werden können, wird der einzig mögliche „bewegende Teil“ im Coulomb-Gesetz sein
. Sein numerischer Wert muss bestimmt werden, und die linke und rechte Seite des Coulombschen Gesetzes fallen zusammen.
Aus grundlegenderer physikalischer Sicht ist die Feinstrukturkonstante die Wechselwirkungskonstante, die die Stärke elektromagnetischer Wechselwirkungen bestimmt. Und vielleicht kann die Physik eines Tages den Wert der Feinstrukturkonstante berechnen, aber davon sind wir noch weit entfernt. Nur die Auswahl von Einheitendefinitionen kann den Wert nicht festlegen
.
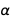
Sind beide wirklich
und
nicht mehr fixiert werden oder ist es möglich, einen von ihnen genau zu halten? Aufgrund der bereits genauen Lichtgeschwindigkeit und des Verhältnisses
wenn einer von
oder
genau, der andere muss auch genau sein. Wir wissen, dass mindestens einer nicht gebunden werden muss, daher müssen beide nicht gebunden sein.
Die Werte, die jetzt durch die Planck-Konstante, die Boltzmann-Konstante, die Avogadro-Konstante und die Elementarladung gegeben sind, sind weder willkürlich noch vollständig definiert. Sie werden mit bis zu ungefähr acht Zeichen bestimmt, sodass die Maßeinheiten, die sie nach dem 20. Mai bestimmen, der "Größe" der Einheiten entsprechen, die sie vor dem 20. Mai bestimmen. Die Zahlen unten rechts sind jedoch nicht definiert. Somit kann der Wert des zukünftigen exakten Wertes der Elementarladung sein
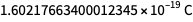
, und nicht
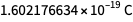
. Es ist Occams Rasiermesser und Rationalität, die es uns ermöglichen, es zu benutzen
.
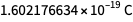
Auf einer technischeren Ebene war die Substitution in der vorherigen Berechnung die durch den Begriff
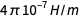
in der Formel
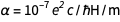amp wurde vor der Neudefinition verwendet (denken Sie daran
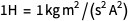
), aber es wurde auch der genaue Wert der Elementarladung verwendet, dh die Definition des Ampere nach Neudefinition. Und wir müssen immer in einem Einheitensystem bleiben.
Berechnung der fehleroptimierten Formulartabelle
Es stellt sich also die natürliche Frage: Was sollen diese „nicht fixierten“ Bedeutungen sein? In meinem letzten Blog habe ich manuell einen neuen Wert erstellt
. Was manuell gemacht werden kann, kann mit einem Computerprogramm gemacht werden. Implementieren wir also ein kleines Programm, das die fehleroptimierte Form von Ableitungen physikalischer Konstanten berechnet. In einem zukunftsorientierten Ansatz ist bereits eine Entitätsklasse mit sieben Konstanten verfügbar, die einen neuen SI definiert.
Unten finden Sie Konstanten, die im neuen SI einen genauen Wert haben.
Die aktuellen Werte dieser Konstanten haben zusammen mit ihrem Fehler (berechnet mit der Funktion
Around []) die Form:
Mit der Entitätsklasse "
PhysicalConstant " können wir neue, bevorstehende Werte physikalischer Größen erhalten. Beachten Sie, dass wie in allen Computersprachen exakte Ganzzahlen und rationale Zahlen entweder explizite Ganzzahlen oder rationale (aber nicht dezimale) Zahlen sind.
Viele physikalische Konstanten können durch Gleichungen in Beziehung gesetzt werden, die durch physikalische Theorien verschiedener Bereiche der Physik gegeben sind. In Zukunft wollen wir uns auf die Theorie grundlegender elektromagnetischer Phänomene beschränken, bei der der Fehler der Konstanten auf den Fehler der Feinstrukturkonstante reduziert wird
und Rydberg-Konstante
. Wenn wir zum Beispiel Gravitationsphänomene einbeziehen würden, müssten wir die Gravitationskonstante G verwenden, die unabhängig gemessen wird, obwohl sie einen sehr großen Fehler aufweist (weshalb die NSF die sogenannte „
Big-G-Herausforderung “ hatte).
Außerdem beschränken wir uns auf elektrische, magnetische und Massengrößen, deren Fehler auf Einheiten reduziert werden
und
.
Im Folgenden verwenden wir die neue
Around- Funktion, um Werte mit entsprechenden Fehlern auszudrücken
und
.
Derzeit ist laut CODATA 2014 der relative Fehler für
geht es um
und für
über
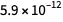
. Wie Sie sehen können, ist der Fehler für
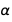
mehr als für
.
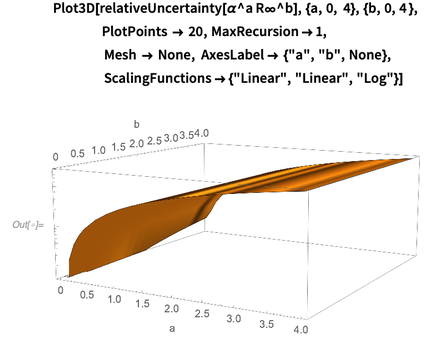
Unten sehen Sie ein Diagramm des relativen Fehlers von Log-Base-10
als Funktionen
a und
b . Offensichtlich hängt der relative Fehler des Produkts für kleine Grade schwach von den Exponenten
a und
b ab . Diese Grafik zeigt, dass die Abhängigkeit des Fehlers
dominiert relativ zu
a (Exponent der Feinstruktur). Diese Beobachtung erklärt sich aus der Tatsache, dass der Fehler der Rydberg-Konstante 50-mal geringer ist als der Fehler der Feinstrukturkonstante.
Um die Fehler verschiedener Konstanten im neuen SI zu berechnen, führen wir die folgenden Schritte aus:
• Abrufen äquivalenter Darstellungen für physikalische Konstanten, auf die über die Entitätsklasse
PhysicalConstant zugegriffen werden kann.
Diese identischen Gleichheiten zwischen physikalischen Konstanten sind die Gesetze der Physik und sollten als solche sowohl im alten als auch im neuen SI erhalten bleiben.
• Stellen Sie sich Formeln als eine Reihe algebraischer Gleichungen vor, auf die verschiedene Ausschlussmethoden angewendet werden können, um eine Konstante durch eine Kombination von sieben Grundkonstanten des neuen SI sowie Feinstrukturkonstanten auszudrücken
und Rydberg-Konstanten
.
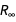
Dies sind die neun Grundkonstanten, die wir in den Definitionen jeder neuen betrachteten Konstante anwenden dürfen. (Technisch gesehen enthält die Liste 10 Konstanten, aber aufgrund der einfachen Skalierungsbeziehung zwischen
h und
ℏ enthält diese Liste tatsächlich neun „verschiedene“ Konstanten.)
Die Entitätsklasse „
PhysicalConstant “ enthält viele Informationen zu den Beziehungen zwischen physischen Konstanten. Hier sind zum Beispiel äquivalente Formen von vier Konstanten, die derzeit gemessen werden und bald als genau identifiziert werden.
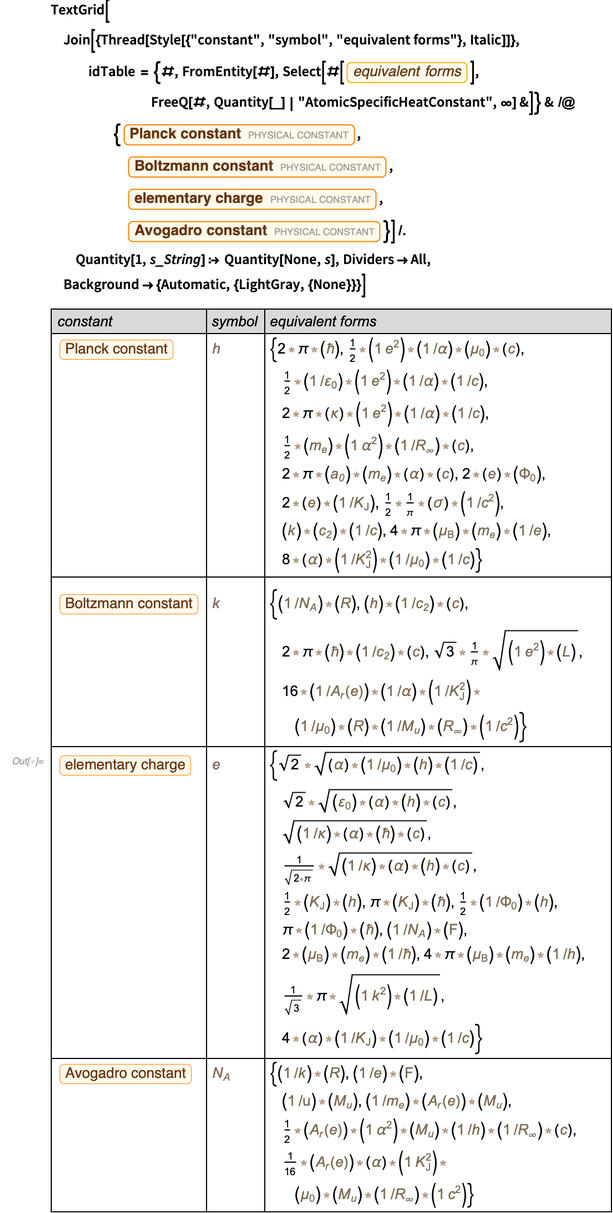
Innerhalb der Genauigkeit der gemessenen Werte arbeiten jetzt alle diese Einheitselemente. Hier ist eine schnelle numerische Überprüfung alternativer Formen der Planck-Konstante. , , .
Around [], .
. .
, . , ? , , , , , .
, , ( ,
Entität [" PhysicalConstant" ,. ] und in Menge [ 1 ,. ] gleichgesetzt werden). Der Grund, warum wir in nachfolgenden Berechnungen Entitäten anstelle von Mengen verwenden, ist zweierlei: Erstens sind Entitäten bequeme, leicht lesbare Darstellungen; und zweitens dringen algebraische Funktionen (wie GroebnerBasis ) nicht in die Größen ein, um die Art ihres ersten Arguments zu bestimmen.
Dann machen wir alle Identitäten polynomisch. Der letzte Schritt bedeutet: (1) Subtrahieren der linken Seite von der rechten Seite; und (2) dass keine Bruchkräfte (z. B. Quadratwurzeln) von Konstanten mehr auftreten. Wir führen eine solche Umwandlung in ein Polynom durch, indem wir nach allen Bruchexponenten suchen und den LCM (kleinsten gemeinsamen Faktor) aller ihrer Nenner finden.
Unten ist eine der vorherigen Gleichungen, die Konstanten mit einer Bruchkraft enthält.
Nach der Polynomisierung kommen wir zu Polynomen mehrerer Variablen in den drei vorhandenen Konstanten. Diese Polynome müssen eliminiert werden.
Die folgende Tabelle zeigt, wie die
toPolynomial- Funktion auf die zuvor gezeigten äquivalenten Formen für eine Elementarladung
angewendet wird. Nach der Heiligsprechung von ℏ in
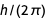
werden einige der resultierenden Polynome identisch.
Basierend auf den verfügbaren physikalischen Konstanten (ohne die Konstanten, die zur Bestimmung des neuen SI verwendet werden) erhalten wir nun genügend äquivalente Formen, um einen Satz von Gleichungen zu erstellen.
Nachfolgend finden Sie eine Liste der erhaltenen Polynomgleichungen für den Ausdruck einer Elementarladung.
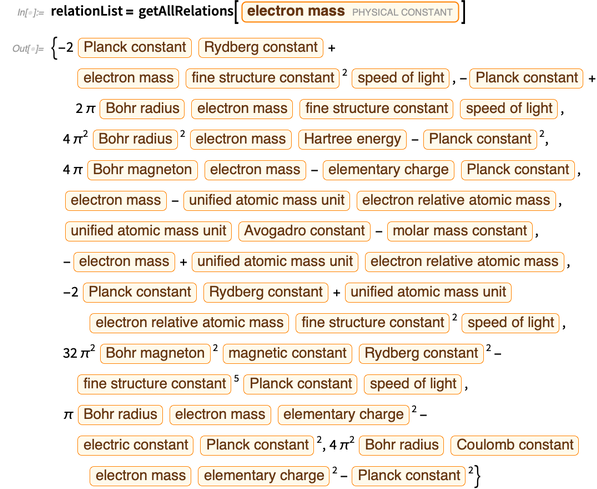
Wir drücken alle Fehler durch die Fehler aus
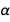
und
. Nur diese beiden Konstanten reichen aus, um den Fehler vieler physikalischer Konstanten auszudrücken. Und da ihre Fehler unabhängig voneinander sind und die Fehler recht klein sind, eignen sich diese beiden ziemlich bekannten Konstanten am besten, um eine optimierte (im Sinne von Fehlern) neue Version vieler physikalischer Konstanten auszudrücken. Und natürlich erlauben wir alle sieben exakten Konstanten aus dem neuen SI; Da es sich um genaue Größen handelt, ändert ihre Anwesenheit den Fehler nicht.
Die Hauptarbeit zum Ausdruck einer gegebenen Konstante in Form von SI-Konstanten und
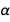
und
wird von der
GroebnerBasis- Funktion implementiert. Das Festlegen des
Parameters MonomialOrder -> ElventionOrder ist ein kritischer Schritt, bei dem alle „unnötigen“ physikalischen Größen entfernt werden und eine Polynomgleichung mit genau definierten Konstanten und (falls erforderlich) Feinstruktur- und Rydberg-Konstanten verbleibt.
Durch Eliminieren der durch die Masse des Elektrons gebundenen Konstanten erhalten wir
.
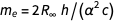
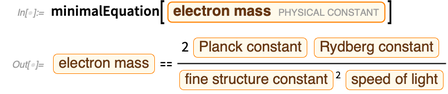
Der Fehler dieses Ausdrucks ergibt sich aus dem Begriff
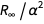
. Wir können eine Funktion definieren, die ein Mitglied entfernt
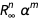
einen Fehler verursachen.
Für eine kompaktere Darstellung können wir eine Funktion definieren, die eine äquivalente Form sowie alte und neue Fehler zurückgibt - in Form einer Zeichenfolge.
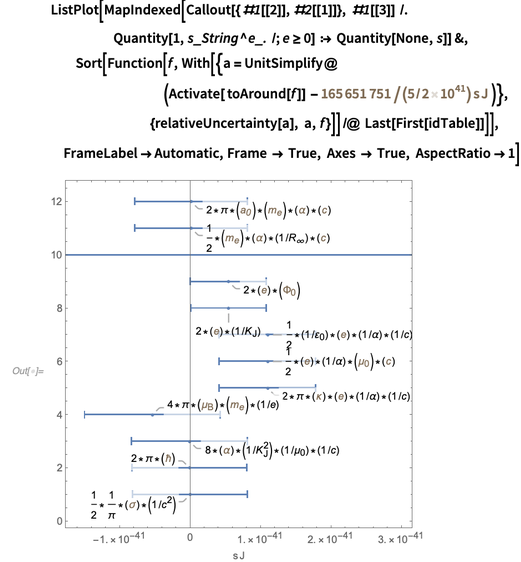
Wir beenden den Blog mit einer Tabelle mit alten und neuen Fehlern für mehr als ein Dutzend physikalische Konstanten. Diese Liste wird als repräsentatives Beispiel ausgewählt. Andere Konstanten können auf ähnliche Weise verarbeitet werden (dies erfordert möglicherweise die Hinzufügung zusätzlicher ungenauer Konstanten zur Konservierung, wie z. B. die Gravitationskonstante oder die Parameter des Standardmodells).
Das Kombinieren der Zeilen in einer Tabelle ergibt das folgende Ergebnis für die optimale Darstellung dieser Konstanten im neuen SI-Einheitensystem.
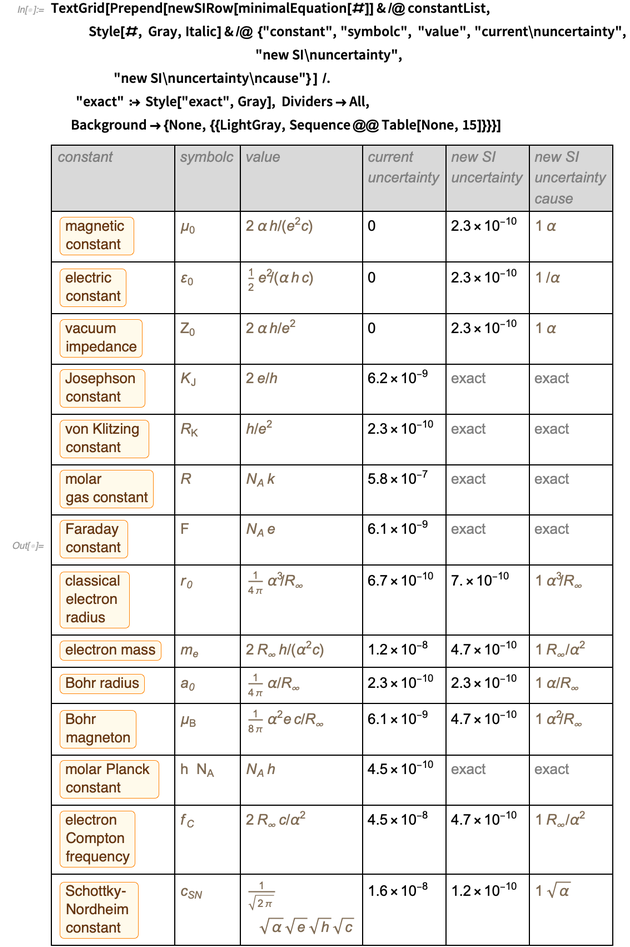
Es war eine Tabelle, die wir anzeigen wollten, und wir haben es geschafft, sie anzuzeigen. Achten Sie auf das Aussehen
im Zähler und Nenner
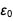
und
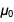
damit nach reduktion das ergebnis
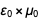
wird
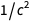
. Eine ähnliche Liste finden Sie unten auf der Wikipedia-Seite zur
Neudefinition von SI-Einheiten .
Jetzt können wir ruhig den Weltmetrologietag
2019 für eine grundlegend bessere Welt erwarten, die durch fundamentale Konstanten beschrieben wird.
Laden Sie den
Wolfram Notebook Blog herunter.
Kostenloses temporäres Wolfram Mathematica SystemHast du eine Frage? Kontaktieren Sie info-russia@wolfram.com