Einführung
Betrachten Sie die diskrete Wavelet-Transformation (DWT), die in der PyWavelets
PyWavelets 1.0.3- Bibliothek implementiert ist. PyWavelets ist eine kostenlose Open-Source-Software, die unter der MIT-Lizenz veröffentlicht wird.
Bei der Verarbeitung von Daten auf einem Computer kann eine diskretisierte Version der kontinuierlichen Wavelet-Transformation durchgeführt werden, deren Grundlagen in meinem vorherigen
Artikel beschrieben wurden . Das Spezifizieren diskreter Werte der Parameter (a, b) von Wavelets mit einem beliebigen Schritt & Dgr; a und & Dgr; b erfordert jedoch eine große Anzahl von Berechnungen.
Darüber hinaus ist das Ergebnis eine übermäßige Anzahl von Koeffizienten, die die Anzahl von Abtastwerten des ursprünglichen Signals weit übersteigt, was für seine Rekonstruktion nicht erforderlich ist.
Die in der PyWavelets-Bibliothek implementierte diskrete Wavelet-Transformation (DWT) liefert genügend Informationen sowohl für die Signalanalyse als auch für ihre Synthese und ist gleichzeitig wirtschaftlich in Bezug auf die Anzahl der Operationen und den erforderlichen Speicher.
Wann wird die Wavelet-Transformation anstelle der Fourier-Transformation verwendet?
Die Fourier-Transformation funktioniert sehr gut, wenn das Frequenzspektrum stationär ist. In diesem Fall sind die im Signal vorhandenen Frequenzen unabhängig von der Zeit, und das Signal enthält die Frequenzen xHz, die irgendwo im Signal vorhanden sind. Je instabil das Signal ist, desto schlechter sind die Ergebnisse. Dies ist ein Problem, da die meisten Signale, die wir im wirklichen Leben sehen, von Natur aus instabil sind.
Die Fourier-Transformation hat im Frequenzbereich eine hohe Auflösung, im Zeitbereich jedoch keine Auflösung. Wir zeigen dies in den folgenden zwei Beispielen.
Auflistungimport numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt
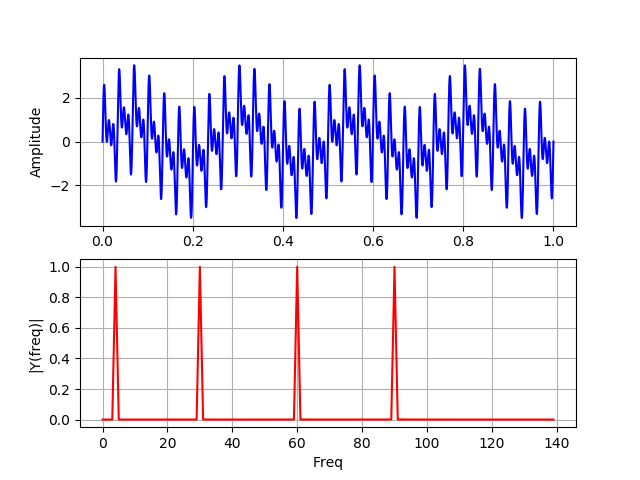
In diesem Diagramm sind alle vier Frequenzen während der gesamten Betriebszeit im Signal vorhanden.
Auflistung import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt
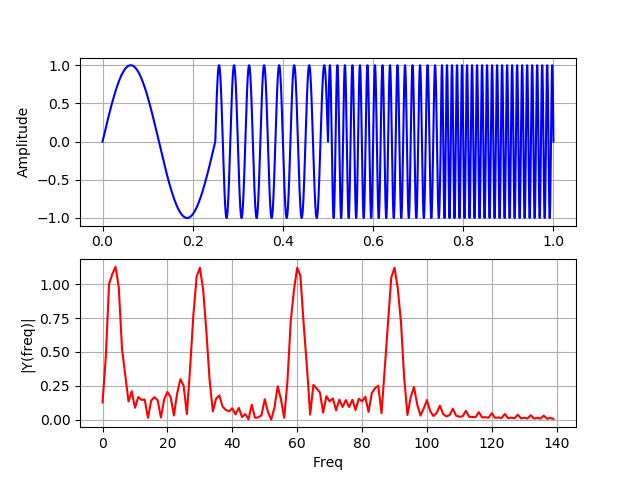
In diesem Diagramm überlappen sich die Signale nicht zeitlich, die Nebenkeulen sind auf eine Lücke zwischen vier verschiedenen Frequenzen zurückzuführen.
Für zwei Frequenzspektren, die genau die gleichen vier Peaks enthalten, kann die Fourier-Transformation nicht bestimmen, wo diese Frequenzen im Signal vorhanden sind. Der beste Ansatz zur Analyse von Signalen mit einem dynamischen Frequenzspektrum ist die Wavelet-Transformation.
Die Haupteigenschaften von Wavelets
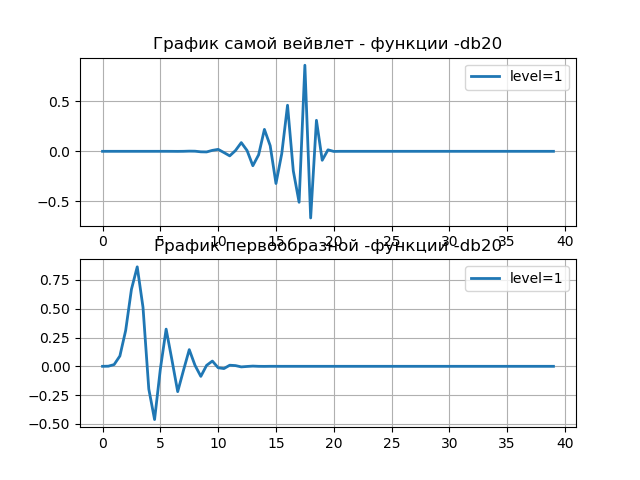
Die Wahl des Typs und damit der Eigenschaften des Wavelets hängt von der Analyseaufgabe ab. Um beispielsweise die effektiven Ströme in der Elektroindustrie zu bestimmen, bieten die Wellenformen höherer Ordnung von Ingrid Daubechies eine größere Genauigkeit. Wavelet-Eigenschaften können mit der Funktion pywt.DiscreteContinuousWavelet () in der folgenden Liste erhalten werden:
Auflistung import pywt from pylab import * from numpy import * discrete_wavelets = ['db5', 'sym5', 'coif5', 'haar'] print('discrete_wavelets-%s'%discrete_wavelets ) st='db20' wavelet = pywt.DiscreteContinuousWavelet(st) print(wavelet) i=1 phi, psi, x = wavelet.wavefun(level=i) subplot(2, 1, 1) title(" - -%s"%st) plot(x,psi,linewidth=2, label='level=%s'%i) grid() legend(loc='best') subplot(2, 1, 2) title(" - -%s"%st) plt.plot(x,phi,linewidth=2, label='level=%s'%i) legend(loc='best') grid() show()
Wir bekommen:
discrete_wavelets - ['db5', 'sym5', 'coif5', 'haar']
Wavelet db20 Family name: Daubechies Short name: db Filters length: 40 Orthogonal: True Biorthogonal: True Symmetry: asymmetric DWT: True CWT: False
In einer Reihe von praktischen Fällen wird es notwendig, Informationen über die Mittenfrequenz des psi-Wavelets zu erhalten, eine Funktion, die beispielsweise bei der Wavelet-Analyse von Signalen zur Erkennung von Defekten in Zahnrädern verwendet wird:
import pywt f=pywt.central_frequency('haar', precision=8 ) print(f)
0.9961089494163424 0.9961089494163424
Mit der Mittenfrequenz
Das mütterliche Wavelet und der Skalierungsfaktor „a“ können Skalen in Pseudofrequenzen umwandeln
unter Verwendung der Gleichung:
Signalerweiterungsmodi
Vor der Berechnung der diskreten Wavelet-Transformation unter Verwendung von
Filterbänken muss
das Signal verlängert werden . Abhängig von der Extrapolationsmethode können an den Signalgrenzen signifikante Artefakte auftreten, die zu Ungenauigkeiten in der DWT-Transformation führen.
PyWavelets bietet verschiedene Signalextrapolationstechniken, mit denen dieser negative Effekt minimiert werden kann. Verwenden Sie die folgende Auflistung, um solche Methoden zu demonstrieren:
Auflistung der Demonstration von Signalerweiterungsmethoden import numpy as np from matplotlib import pyplot as plt from pywt._doc_utils import boundary_mode_subplot

Die Grafiken zeigen, wie sich ein kurzes Signal (rot) (schwarz) über seine ursprüngliche Länge hinaus ausdehnt.
Diskrete Wavelet-Transformation
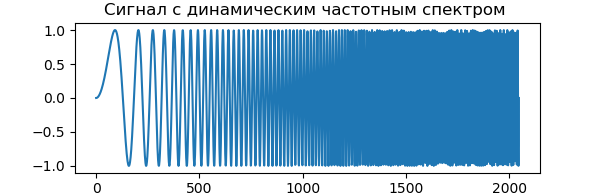
Um die DWT zu demonstrieren, verwenden wir ein Signal mit einem dynamischen Frequenzspektrum, das mit der Zeit zunimmt. Der Anfang des Signals enthält niederfrequente Werte und das Ende des Signals enthält Frequenzen des kurzwelligen Bereichs. Auf diese Weise können wir leicht bestimmen, welcher Teil des Frequenzspektrums herausgefiltert wird, indem wir einfach auf die Zeitachse schauen:
Auflistung from pylab import * from numpy import* x = linspace(0, 1, num=2048) chirp_signal = sin(250 * pi * x**2) fig, ax = subplots(figsize=(6,1)) ax.set_title(" ") ax.plot(chirp_signal) show()
Die diskrete Wavelet-Transformation in PyWavelets 1.0.3 ist die Funktion pywt.dwt (), die die Approximationskoeffizienten cA und die detaillierten Koeffizienten cD der Wavelet-Transformation der ersten Ebene des durch den Vektor angegebenen Signals berechnet:
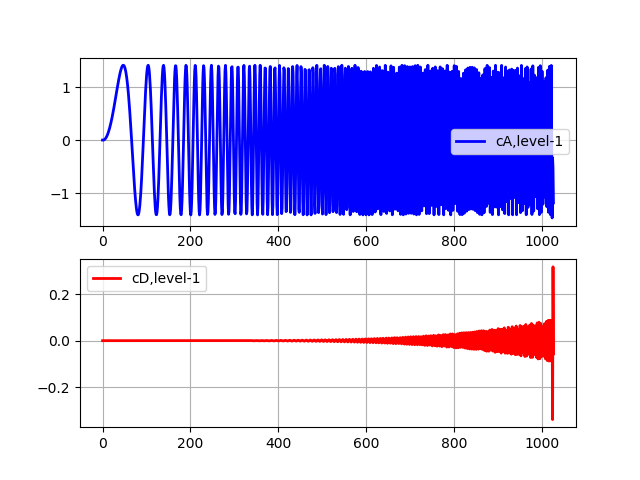
Transformation Level One Listing import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-1') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-1') grid() legend(loc='best') show()
Transformation Level 5 Listing import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()
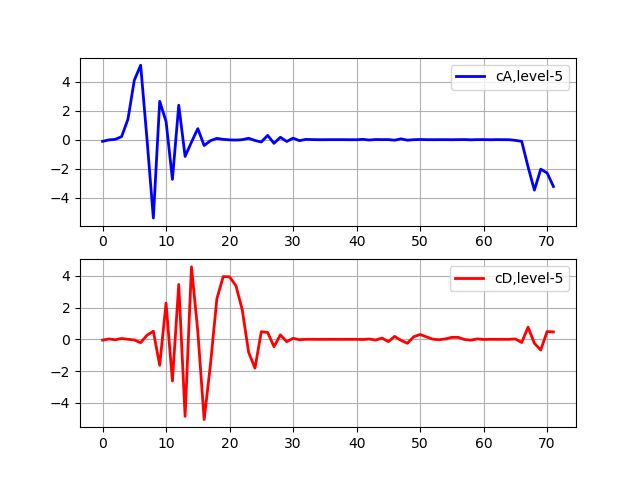
Die Approximationskoeffizienten (cA) repräsentieren die Ausgabe des Tiefpassfilters (Mittelungsfilter) DWT. Die Detailkoeffizienten (cD) repräsentieren die Ausgabe des Hochpassfilters (Differenzfilter) DWT.
Mit der Funktion pywt.wavedec () können Sie sofort übergeordnete Koeffizienten berechnen. Diese Funktion nimmt das Eingangssignal und den Pegel als Eingang und gibt einen Satz von Approximationskoeffizienten (n-ten Pegel) und n Sätze von Detailkoeffizienten (von 1 bis n-ten Pegel) zurück. Hier ist ein Beispiel für die fünfte Ebene:
from pywt import wavedec from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=5) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()
Als Ergebnis erhalten wir die gleichen Grafiken wie im vorherigen Beispiel. Die Koeffizienten cA und cD können getrennt erhalten werden:
Für cA:
import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('a', data, 'db20', mode='symmetric', level=1)
Für cD:
import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('d', data, 'db20', mode='symmetric', level=1)
Filterbank
Einige der Probleme im Zusammenhang mit Conversion-Levels wurden im vorherigen Abschnitt erläutert. DWT wird jedoch immer als Filterbank in Form einer Kaskade von Hochpass- und Tiefpassfiltern implementiert. Filterbänke sind eine sehr effektive Methode, um ein Signal in mehrere Frequenzteilbänder zu unterteilen.
In der ersten Phase mit kleinem Maßstab wird das Hochfrequenzverhalten des Signals analysiert. In der zweiten Stufe nimmt die Skala um den Faktor zwei zu (die Frequenz nimmt um den Faktor zwei ab), und wir analysieren das Verhalten von etwa der Hälfte der maximalen Frequenz. In der dritten Stufe beträgt der Skalierungsfaktor vier, und wir analysieren das Frequenzverhalten von etwa einem Viertel der Maximalfrequenz. Und das geht so weiter, bis wir das maximale Zersetzungsniveau erreicht haben.
Der maximale Zerlegungsgrad kann mit der Funktion pywt.wavedec () berechnet werden, während Zerlegung und Detail wie folgt aussehen:
Auflistung import pywt from pywt import wavedec from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data= sin (250 * pi * x**2) n_level=pywt.dwt_max_level(len(data), 'sym5') print(' : %s'%n_level) x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=7) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-7') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-7') grid() legend(loc='best') show()
Wir bekommen:
Maximale Zersetzungsstufe: 7
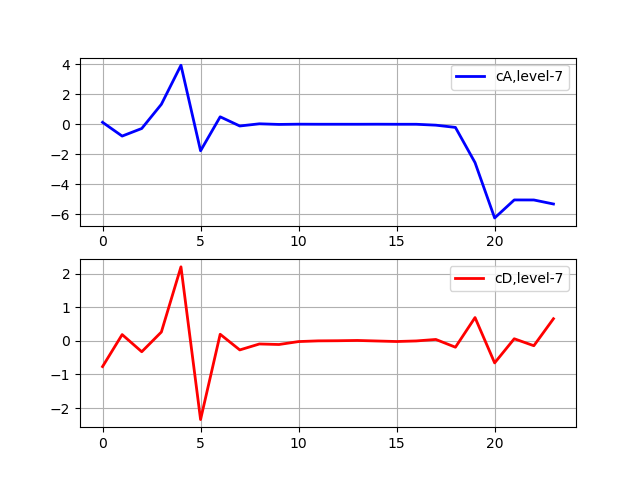
Die Zerlegung stoppt, wenn das Signal für ein gegebenes sym5-Wavelet kürzer als die Filterlänge wird. Angenommen, wir haben ein Signal mit Frequenzen bis zu 1000 Hz. In der ersten Stufe trennen wir unser Signal in niederfrequente und hochfrequente Teile, d. H. 0-500 Hz und 500-1000 Hz. In der zweiten Stufe nehmen wir den niederfrequenten Teil und teilen ihn erneut in zwei Teile: 0-250 Hz und 250-500 Hz. In der dritten Stufe haben wir den Teil 0-250 Hz in den Teil 0-125 Hz und den Teil 125-250 Hz unterteilt. Dies setzt sich fort, bis wir das maximale Zersetzungsniveau erreicht haben.
Analyse von WAV-Dateien mit fft Fourier- und Wavelet-Skalogrammen
Verwenden Sie zur Analyse die
WebSDR-Datei . Betrachten Sie die Analyse des reduzierten Signals mit triang aus scipy.signal und die Implementierung der diskreten Fourier-Transformation in Python (fft aus scipy.fftpack). Wenn die Länge der Sequenz fft nicht gleich 2n ist, wird anstelle der schnellen Fourier-Transformation (fft) eine diskrete Fourier-Transformation (dft) durchgeführt. So arbeitet dieses Team.
Wir verwenden den schnellen Fourier-Transformationspuffer nach folgendem Schema (z. B. numerische Daten):
fftbuffer = np.zeros (15); Erstellen Sie einen mit Nullen gefüllten Puffer.
fftbuffer [: 8] = x [7:]; Verschieben Sie das Ende des Signals in den ersten Teil des Puffers. fftbuffer [8:] = x [: 7] - Wir verschieben den Anfang des Signals zum letzten Teil des Puffers. X = fft (fftbuffer) - Wir betrachten die Fourier-Transformation eines mit Signalwerten gefüllten Puffers.
Um das Phasenspektrum besser lesbar zu machen, ist die Phasenbereitstellung anwendbar. Ändern Sie dazu die Linie mit der Berechnung der Phasenkennlinie: pX = np.unwrap (np.angle (X)).
Auflistung für die fft-Signalfragmentanalyse import numpy as np from pylab import * from scipy import * import scipy.io.wavfile as wavfile M=501 hM1=int(np.floor((1+M)/2)) hM2=int(np.floor(M/2)) (fs,x)=wavfile.read('WebSDR.wav') x1=x[5000:5000+M]*np.hamming(M) N=511 fftbuffer=np.zeros([N]) fftbuffer[:hM1]=x1[hM2:] fftbuffer[N-hM2:]=x1[:hM2] X=fft(fftbuffer) mX=abs(X) pX=np.angle(X) suptitle(" WebSDR") subplot(3, 1, 1) st=' (WebSDR.wav)' plot(x,linewidth=2, label=st) legend(loc='center') subplot(3, 1, 2) st=' ' plot(mX,linewidth=2, label=st) legend(loc='best') subplot(3, 1, 3) st=' ' pX=np.unwrap(np.angle(X)) plot(pX,linewidth=2, label=st) legend(loc='best') show()

Für die vergleichende Analyse verwenden wir ein Wavelet-
Skalogramm , das mit der Funktion tree = pywt.wavedec (Signal, 'coif5') in matplotlib erstellt werden kann.
Auflisten von Wavelet-Skalogrammen from pylab import * import pywt import scipy.io.wavfile as wavfile
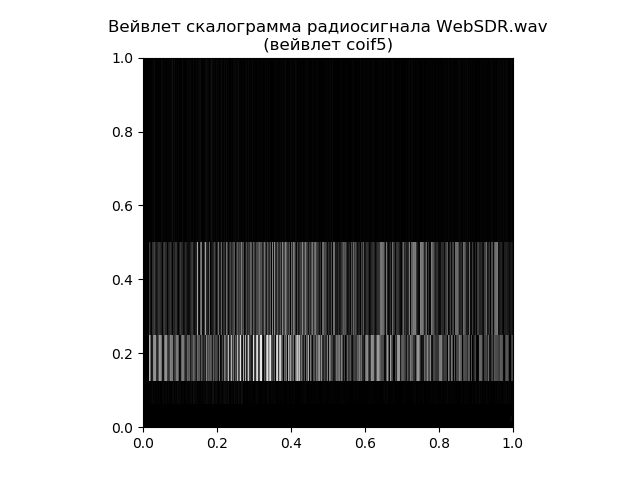
Somit gibt das Skalogramm eine detailliertere Antwort auf die Frage der Verteilung der Frequenzen über die Zeit, und die schnelle Fourier-Transformation ist für die Frequenzen selbst verantwortlich. Es hängt alles von der Aufgabe ab, auch für ein so einfaches Beispiel.
Schlussfolgerungen
- Die Gründe für die Verwendung einer diskreten Wavelet-Transformation für dynamische Signale werden angegeben.
- Beispiele für die Wavelet-Analyse mit PyWavelets 1.0.3, einer kostenlosen Open Source-Software, die unter der MIT-Lizenz veröffentlicht wurde, werden bereitgestellt.
- Software-Tools für die praktische Verwendung der PyWavelets-Bibliothek werden berücksichtigt.