Wenn wir ein Olympiadenproblem analysieren, werden wir die gewundenen Korridore der Erzeugung von Labyrinthen und ihren Durchgang entlang gehen, und wir werden auch sehen, dass in der Julia-Sprache die Einfachheit der Implementierung von Algorithmen an ihren Pseudocode grenzt.

Herausforderung

Das Labyrinth ist ein kariertes Quadrat von 10 mal 10, in einigen Zellen gibt es Hindernisse und in einer Zelle gibt es einen Ausgang. Der Roboter befindet sich in einem solchen Labyrinth und kann 4 Befehle ausführen: eine Zelle nach unten, oben, rechts oder links bewegen. Wenn der Roboter versucht, die Grenzen des Labyrinths zu überschreiten oder mit einem Hindernis in den Käfig zu gelangen, bleibt er an Ort und Stelle. Wenn der Roboter den Ausgang betritt, verlässt er das Labyrinth und ignoriert weitere Befehle. Schreiben Sie ein Programm für den Roboter, das den Roboter auf jeden Fall zum Ausgang bringt, unabhängig von der Zelle, in der er sich am Anfang befand. Das Programm sollte aus nicht mehr als 1000 Teams bestehen.

Eingabeformat

Es gibt keinen Eintrag. Sie müssen ein Programm für eine bestimmte angegebene Bedingung schreiben
das Labyrinth.
Die Version des Labyrinths, die Sie kopieren können. 0 - freie Zelle, 1 - Hindernis, x -
Ausweg.

0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000 

Ausgabeformat

Eine Zeile besteht aus den Zeichen U, D, R, L mit einer Länge von nicht mehr als 1000

Vorbereitung

Diejenigen, die in Julia nicht mit Grafiken gearbeitet haben, müssen Pakete herunterladen

 using Pkg Pkg.add("Plots") Pkg.add("Colors") Pkg.add("Images") Pkg.build("Images") #     

Es ist am bequemsten, in Jupyter zu arbeiten, da die Bilder direkt während der Arbeit angezeigt werden. Hier finden Sie Informationen zur Installation sowie eine Einführung und Aufgaben für Anfänger.

Im Rahmen unserer Aufgabe gibt es eine Version des Labyrinths zum Kopieren

 S0 = "0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000" 

Um ein Labyrinth zu zeichnen, müssen Sie eine Matrix erstellen. Da wir keine Leerzeichen manuell einfügen möchten, arbeiten wir mit der Zeile:

 S1 = prod(s-> s*' ', '['*S0*']') # prod(fun, arr)    arr #     fun #  julia  *   "[ 0 0 1 1 0 1 0 0 1 1 \n 0 1 0 0 0 0 1 0 0 0 \n 0 1 1 0 x 0 0 0 0 0 \n 0 0 1 0 0 0 0 1 0 0 \n 0 0 0 0 1 1 1 0 0 0 \n 0 0 0 0 1 0 0 1 0 0 \n 0 0 0 0 0 1 0 0 1 0 \n 0 1 0 0 1 0 1 0 1 0 \n 0 0 1 1 0 0 1 0 1 0 \n 1 0 0 0 0 1 1 0 0 0 ] " 

Wenn wir den umständlichen Buchstaben x durch eine Zahl ersetzen und die Zeichenfolge analysieren, erhalten wir eine Ganzzahlmatrix, die unser Labyrinth definiert. Ändern Sie dann zur Vereinfachung die Einsen in Nullen und die Nullen in Einsen und schließen Sie das Labyrinth mit einer Wand ein:

 S2 = replace(S1, 'x'=>'9') M0 = S2 |> Meta.parse |> eval m,n = size(M0) M1 = replace(M0, 1=>0, 0=>1) M = zeros(Int64,m+2,n+2) for i in 2:m+1, j in 2:n+1 M[i,j] = M1[i-1,j-1] end M # Maze map matrix 12×12 Array{Int64,2}: 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 

In der Matrix

 length(M) 144 

Zellen und von ihnen

 sum(M)-9 70 

auf denen man laufen kann, also - mögliche Startpositionen. Sie können das Ergebnis anzeigen, indem Sie ein zweidimensionales Histogramm erstellen

 using Plots heatmap(M, yaxis = :flip) # flip -   

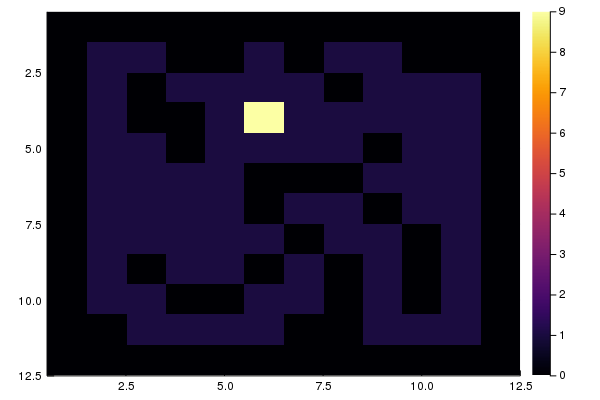
Lösungsüberprüfung

Zunächst müssen Sie Verfahren ausarbeiten, mit denen die Richtigkeit der vorgeschlagenen Lösung überprüft wird. Legen Sie den zusammengesetzten Typ Point , um die Terminologie von Punkten und Koordinaten zu verwenden:

 mutable struct Point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end 

Und jetzt müssen Sie lernen, wie Sie eine Folge von Befehlen, die für den Roboter verständlich sind, in Code übersetzen.

Die Idee ist ganz einfach: Es gibt eine Startkoordinate, eine Linie enthält einen Algorithmus, der erklärt, wie man geht. Wir nehmen einen Buchstaben und schauen uns an, auf welche der Nachbarzellen wir treten sollen. Zur aktuellen Koordinate addieren wir den Wert, der in dieser Zelle gespeichert ist. Das heißt, wenn es Null (Wand) gibt, haben wir uns nirgendwo bewegt, sonst haben wir einen kleinen Schritt in die gewünschte Richtung gemacht.

Mit der Kraft der Metaprogrammierung können Sie die eingehende Richtungsfolge durch einen sperrigen, einheitlichen Code ersetzen und ausführen

 S = "RRLDUURULDDRDDRRRUUU" S1 = replace(S , "R"=>"c.y+=M[cx, c.y+1];") S1 = replace(S1, "L"=>"cy-=M[cx, cy-1];") S1 = replace(S1, "U"=>"c.x+=M[c.x+1, cy];") S1 = replace(S1, "D"=>"cx-=M[cx-1, cy];") #  - start point Sp = eval( Meta.parse(S1) ) 

Diese Methode weist jedoch eine Reihe von Unannehmlichkeiten auf. Daher werden wir die klassischen bedingten Operatoren verwenden. Übrigens ist die Tatsache, dass die Ausgabe durch die Nummer 9 angezeigt wird, ein kleiner Trick: Um nicht jede Zelle zu überprüfen und ob es der Ausweg ist, initiieren wir die Bewegung, indem wir den in einer bestimmten Zelle gespeicherten Wert addieren. Wenn der Roboter den Ausgang betritt, wird seiner Koordinate eine absichtlich große Zahl hinzugefügt, sodass der Roboter über die Grenzen des Arrays hinaus fliegt, was mit dem Block als Fehler abgefangen werden kann:

 try #     catch #       end 

Daher implementieren wir eine Funktion, die überprüft, ob der Roboter ab Punkt c den Ausgang erreicht, c er Befehle aus der Zeichenfolge str ausführt:

 function isexit(str, c) scatter!([cy],[cx]) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end 

Sammeln wir eine Funktion, die über alle Startpositionen iteriert

 function test(Str) k = 0 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

Überprüfen Sie die Befehle:

 S = "RRRLDUUURRRUUURRRRLLLRRUULDDDDRRRRDDDRRRUUU" heatmap(M, yaxis = :flip) test(S) # 10 test completed from 70 plot!(legend = false) 

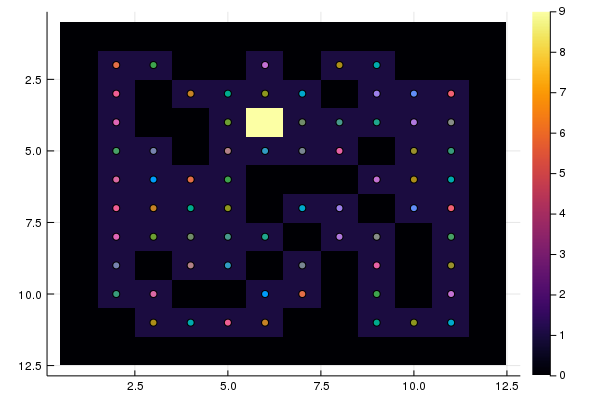
Alle Startpunkte wurden getestet und nur 10 führten zum Ausgang. Es ist notwendig, Routen von jedem Punkt bis zum Ausgang zu erstellen.

Bevor wir uns mit der Erzeugung und Passage der Labyrinthe befassen, werden wir unsere Ergebnisse speichern. Wir werden das Paket Images.jl verwenden, das viele Möglichkeiten im Bereich der Bildverarbeitung bietet (ein gutes Beispiel ). Eines seiner unterstützenden Werkzeuge ist das Colors.jl- Paket, das Julias Fähigkeit erweitert, mit Farben zu arbeiten.

 using Images clrs(x) = x==9 ? RGB(1.,0.5,0) : RGB(x,x,x) maze = clrs.(M) # maze = Gray.(maze) # save("D:/dat/maze12x12.png", maze) 

Tiefensuche

Umsetzung der Idee aus einem Artikel über den Habr .
Die Idee ist einfach: Erstellen Sie ein Gitter aus Wänden

 M = 10 N = 10 A = [ i&j&1 for i in 0:N, j in 0:M ] # isodd(i) & isodd(j) & 1 Gray.(A) # from Images.jl 

Dann durchbrechen wir die Route und die Zweige. Wir definieren eine Funktion, die benachbarte nicht besuchte Bereiche findet (wir werden sie beispielsweise durch einen Deuce bezeichnen) und einen dieser Nachbarn zurückgibt (wenn es keine nicht besuchten Nachbarn gibt, gibt sie einen Flaggenpunkt zurück):

 function neighbours2(A,p, n, m) nbrs = [Point(px, p.y+2), # up Point(px, py-2), # down Point(px-2, py), # left Point(p.x+2, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==2 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(-1,-1) end 

Wir werden die Mauern so brechen:

 function breakwall(A, newp,oldp) #  : x = (newp.x + oldp.x) >> 1 #   y = (newp.y + oldp.y) >> 1 A[x,y] = 1 end 

Algorithmus

1. Machen Sie die anfängliche Zelle aktuell und markieren Sie sie als besucht.
2. Während es nicht besuchte Zellen gibt
   1. Wenn die aktuelle Zelle "Nachbarn" nicht besucht hat
   1. Schieben Sie die aktuelle Zelle auf den Stapel
   2. Wählen Sie eine zufällige Zelle aus dem Nachbarland aus
   3. Entfernen Sie die Wand zwischen der aktuellen Zelle und der ausgewählten
   4. Machen Sie die ausgewählte Zelle aktuell und markieren Sie sie als besucht.
   2. Andernfalls, wenn der Stapel nicht leer ist
   1. Ziehen Sie den Käfig aus dem Stapel
   2. Machen Sie es aktuell
   3. Sonst
   1. Wählen Sie eine zufällige nicht besuchte Zelle aus, machen Sie sie aktuell und markieren Sie sie als besucht.

 function amazeng(n, m) M = [ 2(i&j&1) for i in 0:n, j in 0:m ]; p = Point(2,2) #   lifo = [] #   push!(lifo, p) #i = 0 while length(lifo) != 0 #     M[px,py] = 1 #     np = neighbours2(M, p, n, m) # new point #    -   if np.x == np.y == -1 p = pop!(lifo) else push!(lifo, p) breakwall(M, np, p) p = np #i+=1 #maze = Gray.(M/2) #save("D:/dat/maze$i.png", maze) end end M[1,2] = 1 #  M[n,m+1] = 1 #  Gray.(M) end 

 lbrnt = amazeng(36, 48) # save("D:/dat/maze111.png", lbrnt) 

Backtracking-Pfad-Suchalgorithmus:

1. Machen Sie die anfängliche Zelle aktuell und markieren Sie sie als besucht.
2. Bis eine Lösung gefunden ist
   1. Wenn die aktuelle Zelle "Nachbarn" nicht besucht hat
   1. Schieben Sie die aktuelle Zelle auf den Stapel
   2. Wählen Sie eine zufällige Zelle aus dem Nachbarland aus
   3. Machen Sie die ausgewählte Zelle aktuell und markieren Sie sie als besucht.
   2. Andernfalls, wenn der Stapel nicht leer ist
   1. Ziehen Sie den Käfig aus dem Stapel
   2. Machen Sie es aktuell
   3. Sonst gibt es keinen Ausweg.

Wir suchen Nachbarn im Gegenteil und innerhalb des Radius einer Zelle und nicht durch eine:

 function neighbours1(A, p, n, m) nbrs = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==1 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(0,0) end 

Definieren Sie einen Algorithmus zum Überholen des Labyrinths mit Zeichnen der Route und erfolglosen Versuchen

 function amazeng(img, start, exit) M = Float64.(channelview(img)) n, m = size(M) p = start M[exit.x,exit.y] = 1 lifo = [] push!(lifo, p) while px != exit.x || py != exit.y M[px,py] = 0.4 np = neighbours1(M, p, n, m) if np.x == np.y == 0 M[px,py] = 0.75 p = pop!(lifo) #  -  ,    #      else push!(lifo, p) p = np end end Gray.(M) end 

Wie einige bemerkt haben, wird auch eine Funktion aufgerufen, wie die, die die Algorithmen generieren (Multiple Scheduling). Wenn Sie es mit zwei Zahlen aufrufen, wird die Methode zum Erstellen des Labyrinths ermittelt. Wenn Sie es jedoch aufrufen, indem Sie das Bild und zwei Punkte (die Koordinaten der Eingabe und Ausgabe) als Argument angeben, erhalten wir bei der Ausgabe ein Bild mit dem übergebenen Labyrinth

 img0 = load("D:/dat/maze111.png") amazeng(img0) 

Probieren wir unser Labyrinth an:

 img0 = load("D:/dat/maze12x12.png") n, m = size(img0) amazeng(img0, Point(11,9), Point(4,6) ) 

Selbst wenn Sie die Funktion so ändern, dass die Route gespeichert wird, erweist sich der Algorithmus aufgrund der offenen Räume als unwirksam. Aber die Labyrinthe kommen großartig heraus.

Prims randomisierter Algorithmus

Sobald Sie anfangen, Labyrinthe zu zeichnen, werden Sie nicht mehr aufhören. Lassen Sie uns einen weiteren interessanten Algorithmus ausführen:

• Beginnen Sie mit einem Gitter voller Wände.
• Wählen Sie eine Zelle aus und markieren Sie sie als Teil des Labyrinths. Fügen Sie der Wandliste Zellwände hinzu.
• Während es Wände in der Liste gibt:
  
  • Wählen Sie eine zufällige Wand aus der Liste. Wenn nur eine der beiden Zellen besucht wird, die die Wand teilt, dann:
    
    • Machen Sie die Wand zu einem Durchgang und markieren Sie die nicht besuchte Zelle als Teil des Labyrinths.
    • Fügen Sie der Wandliste benachbarte Zellwände hinzu.
  • Entfernen Sie die Wand von der Liste.

 neighbors(p::Point) = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right function newalls!(walls, p, maze, n, m) nbrs = neighbors(p) for a in nbrs if 1<ax<n-1 && 1<ay<m-1 && !maze[ax,ay] push!(walls, a) #       . end end end function breakwall!(p, maze, n, m) nbrs = neighbors(p) #       if sum( a-> maze[ax,ay], nbrs) == 1 for a in nbrs if maze[ax,ay] # true =  px == ax ? nx = px : px>ax ? nx = p.x+1 : nx = px-1 py == ay ? ny = py : py>ay ? ny = p.y+1 : ny = py-1 maze[px,py] = true #   maze[nx,ny] = true px = nx py = ny return true end end else return false end end function prim(n, m) M = falses(n,m); #    p = Point(2, 2) M[px,py] = true walls = [] newalls!(walls, p, M, n, m) while length(walls) != 0 p = splice!( walls, rand(1:length(walls)) ) if breakwall!(p, M, n, m) newalls!(walls, p, M, n, m) end end M end 

 primaze = prim(19,19); Gray.(primaze) 

Es wird verzweigter und nicht weniger beeindruckend, insbesondere der Montageprozess.

Und jetzt implementieren wir den gängigsten Algorithmus, um den kürzesten Weg zu finden:

Methode A *

• Es werden 2 Scheitelpunktlisten erstellt - ausstehend und bereits überprüft. Zu den ausstehenden wird ein Startpunkt hinzugefügt, die Liste der bisher überprüften ist leer.
• Für jeden Punkt wird berechnet $$$H$ - die ungefähre Entfernung vom Punkt zum Ziel.
• Aus der Liste der zu berücksichtigenden Punkte den Punkt mit dem kleinsten $$$H$ . Lass sie $$$X$ .
• Wenn $$$X$ - das Ziel, dann haben wir die Route gefunden.
• Wir tragen $$$X$ von der ausstehenden Liste zur Liste der bereits überprüften.
• Für jeden der Punkte neben $$$X$ (bezeichnen diesen benachbarten Punkt $$$Y$ ), mache folgendes:
  
  • Wenn $$$Y$ bereits in der Überprüfung - überspringen Sie es.
  • Wenn $$$Y$ noch nicht auf der Warteliste - dort hinzufügen.
• Wenn die Liste der zu berücksichtigenden Punkte leer ist, wir das Ziel jedoch nicht erreicht haben, ist die Route nicht vorhanden.

Definieren wir zunächst die Klasse "Punkt", die weiß, wie weit sie vom Ziel entfernt ist:

 mutable struct Point_h x::Int64 # horisont y::Int64 # vertical h::Float64 Point_h(x, y) = new(x, y, 0.) end 

Nun definieren wir eine Vergleichsoperation für die Struktur, eine Methode zum Feststellen des Vorhandenseins eines Elements in einem Array sowie die Funktion zum Entfernen eines Elements, zum Ermitteln des Abstands zwischen Punkten und zum Auflisten von Nachbarn:

 import Base: in, == ==(a::Point_h, b::Point_h) = ax==bx && ay==by function in(p::Point_h, Arr::Array{Point_h,1}) for a in Arr if a == p return true end end return false end function splicemin!(Arr)#::Array{Point_h,1} i = argmin( [ah for a in Arr] ) splice!(Arr, i) end dista(u,v) = hypot(vx-ux, vy-uy) # <=> sqrt( (vx-ux)^2 + (vy-uy)^2 ) neighbors(p::Point_h) = [Point_h(px, p.y+1), # up Point_h(px, py-1), # down Point_h(px-1, py), # left Point_h(p.x+1, py)] # right 

Wie immer können obskure Operatoren mit dem Befehl geklärt werden ? B. ?splice ?argmin .

Und eigentlich die Methode A * selbst

 function astar(M, start, final) #   -       isgood(p) = 1<px<n && 1<py<m && M[px,py] != 0 n, m = size(M) #       start.h = dista(start,final) closed = [] opened = [] push!(opened, start) while length(opened) != 0 X = splicemin!(opened) if X in closed continue end if X == final break end push!(closed, X) nbrs = neighbors(X) ygrex = filter(isgood, nbrs) for Y in ygrex if Y in closed continue else Yh = dista(Y, final) push!(opened, Y) end end end #    closed # return end 

Wir laden das Bild mit dem Labyrinth und präsentieren es in Form einer Matrix:

 img0 = load("D:/dat/maze0.png") mazematrix = Float64.(channelview(img0)) 

Und wir bauen eine Route, um einen beliebigen Punkt zu verlassen:

 s = Point_h(11,9) # start f = Point_h(4,6) # finish M = copy(mazematrix) route = astar(M, s, f) i = 1 for c in route #   M[cx,cy] = 0.7 #save("D:/dat/Astar$i.png", M) i+=1 end Gray.(M) 

Eine Suche aus allen Positionen sieht folgendermaßen aus:

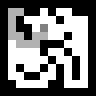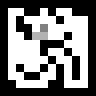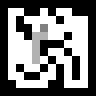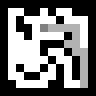
Gesehen, dass der Agent eilen neigt immer zur Seite des Ausgangs und verwandelt sich oft in Sackgassen, was zu unnötigen Schritten führt, und die gesamte Route wird in Erinnerung behalten. Dies wird durch eine etwas komplexere Version des A * -Algorithmus vermieden.

• Es werden 2 Scheitelpunktlisten erstellt - ausstehend und bereits überprüft. Zu den ausstehenden wird ein Startpunkt hinzugefügt, die Liste der bisher überprüften ist leer.
• Für jeden Punkt wird berechnet $$$F = G + H$ . $$$G$ - Abstand vom Start zum Punkt, $$$H$ - die ungefähre Entfernung vom Punkt zum Ziel. Jeder Punkt speichert auch einen Link zu dem Punkt, von dem er kam.
• Aus der Liste der zu berücksichtigenden Punkte den Punkt mit dem kleinsten $$$F$ . Lass sie $$$X$ .
• Wenn $$$X$ - das Ziel, dann haben wir die Route gefunden.
• Wir tragen $$$X$ von der ausstehenden Liste zur Liste der bereits überprüften.
• Für jeden der Punkte neben $$$X$ (bezeichnen diesen benachbarten Punkt $$$Y$ ), mache folgendes:
  
  • Wenn $$$Y$ bereits in der Überprüfung - überspringen Sie es.
  • Wenn $$$Y$ noch nicht auf der Warteliste - fügen Sie es dort hinzu und merken Sie sich den Link zu $$$X$ und berechnet haben $$$Y.G$ (Das $$$X.G$ + Entfernung von $$$X$ vorher $$$Y$ ) und $$$Y.H$ .
  • Wenn $$$Y$ in der Liste zur Prüfung - prüfen Sie, ob $$$X.G$ + Entfernung von $$$X$ vorher $$$Y$$$$<Y.G$ Also kamen wir zur Sache $$$Y$ kürzerer Weg, ersetzen $$$Y.G$ auf $$$X.G$ + Entfernung von $$$X$ vorher $$$Y$ und der Punkt, von dem sie kamen $$$Y$ auf $$$X$ .
• Wenn die Liste der zu berücksichtigenden Punkte leer ist, wir das Ziel jedoch nicht erreicht haben, ist die Route nicht vorhanden.

Aber auch bei unnötigen Schritten liegt unsere Option im Rahmen der Aufgabe, sodass das Ändern der Programme Ihre Hausaufgabe ist.

Bis zum Ende der Olympiade war nichts mehr übrig, aber wir müssen noch lernen, wie wir die Ergebnisse unserer Algorithmen in Befehle der Form "RRLUUDL..."

Und nach all diesen Spaziergängen durch die Labyrinthe können wir davon ausgehen, dass die Lösung viel einfacher ist. Tatsächlich bittet eine einfache Option sofort, aber ich wollte wirklich schöne Dinge machen .

Wenn wir unseren Künstler auf freiem Feld platzieren und zufällige Spaziergänge einleiten, wird er in der Nähe seiner Ausgangsposition zögern. Mit der Einführung der Wände beginnen jedoch einige Richtungen zu verblassen, die Freiheitsgrade werden geringer und mit denselben Eingabedaten bewegt sich der Agent eine größere Strecke.

Hier ist unsere Version der Überprüfung von Teams auf Eignung zur Rettung eines Roboters aus einem Labyrinth:

 M = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0] mutable struct Point # point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end function isexit(str, c) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end function test(Str) k = 0 n, m = 10,10 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

Jetzt reicht es aus, zufällige Linien zu generieren, bis Sie eine erhalten, die für alle Startpositionen funktioniert:

 using Random S = randstring("RLUD",200) "RDRRRDLRLUULURUDUUDLLLLLULLUDRRURDLDLULLRLUUUDURUUUULRUDUURUUDLRLLULRLUDRRLRRULLDULRRRRULRLLDULRLDRUDURDRUUDUUDDDDDLURRRRDRDURRRDDLLDUURRRLDRUDLRLLRDDRLRRRDDLLLRUURDRLURDLLUULLLLUURLLULUDULDDLDLLRLDUD" test(S) 41 test completed from 70 

Außerdem war es möglich, sich nicht um den Test zu kümmern. Es genügte, die Aufgabe zu lesen und eine zufällige Zeichenfolge mit der maximal zulässigen Bedingung zu generieren:

 for i in 1:20 S = randstring("RLUD",1000) test(S) end 70 test completed from 70 70 test completed from 70 70 test completed from 70 70 test completed from 70 55 test completed from 70# 65 test completed from 70# 70 test completed from 70 70 test completed from 70 38 test completed from 70# 70 test completed from 70 70 test completed from 70 56 test completed from 70# 70 test completed from 70 70 test completed from 70 70 test completed from 70 16 test completed from 70# 70 test completed from 70 24 test completed from 70# 70 test completed from 70 70 test completed from 70 

Das heißt, mit einer Wahrscheinlichkeit von 70% würde die Linie die Tests bestehen.

Das ist alles Ich wünsche dem Leser eine erfolgreiche Zufälligkeit, Geduld und Intuition für offensichtliche Lösungen.

Für die Neugierigen - Links zur Vertiefung des Themas:

• Der vollständigste Ausflug in die Labyrinthgeneration
• Russische Version
• Times Methoden
• Zwei Methoden
• Eller-Algorithmus
• Online-Generator
• Methoden zum Online-Finden des Pfades zwischen Punkten
• Sprungpunkt-Suchpfad-Algorithmus
• A * auf Wikipedia
• Einführung in A *
• Einführung in Algorithmus A *
• Erklärung der Pfadfindungsalgorithmen
• Kunstquelle