Dieser Kommentar wurde durch das Schreiben des Artikels veranlasst. Genauer gesagt, ein Satz davon.

... Speicher oder Prozessorzyklen für Artikel in Milliarden von Dollar auszugeben ist nicht gut ...

So kam es, dass ich kürzlich genau das tun musste. Und obwohl der Fall, den ich in diesem Artikel betrachten werde, etwas Besonderes ist - die Schlussfolgerungen und angewandten Lösungen können für jemanden nützlich sein.

Ein bisschen Kontext

Die iFunny-Anwendung verarbeitet eine große Menge an Grafik- und Videoinhalten, und die unscharfe Suche nach Duplikaten ist eine der sehr wichtigen Aufgaben. Dies ist an sich ein großes Thema, das einen separaten Artikel verdient, aber heute werde ich nur ein wenig über einige Ansätze zur Berechnung sehr großer Zahlenfelder in Bezug auf diese Suche sprechen. Natürlich hat jeder ein anderes Verständnis von "sehr großen Arrays", und es wäre dumm, mit dem Hadron Collider zu konkurrieren, aber immer noch. :) :)

Wenn der Algorithmus sehr kurz ist, wird für jedes Bild seine digitale Signatur (Signatur) aus 968 Ganzzahlen erstellt, und der Vergleich wird durchgeführt, indem der "Abstand" zwischen den beiden Signaturen ermittelt wird. Wenn man bedenkt, dass das Inhaltsvolumen allein in den letzten zwei Monaten etwa 10 Millionen Bilder betrug, wird ein aufmerksamer Leser es leicht in seinem Kopf herausfinden - dies sind genau die „Elemente in Milliarden von Volumen“. Wen kümmert es - willkommen bei Katze.

Am Anfang wird es eine langweilige Geschichte über das Sparen von Zeit und Gedächtnis geben, und am Ende wird es eine kurze lehrreiche Geschichte darüber geben, dass es manchmal sehr nützlich ist, sich die Quelle anzusehen. Ein Bild, das Aufmerksamkeit erregt, steht in direktem Zusammenhang mit dieser lehrreichen Geschichte.

Ich muss zugeben, dass ich ein bisschen gerissen war. In einer vorläufigen Analyse des Algorithmus konnte die Anzahl der Werte in jeder Signatur von 968 auf 420 reduziert werden. Sie ist bereits doppelt so gut, aber die Größenordnung bleibt gleich.

Wenn Sie darüber nachdenken, ist es nicht so sehr, dass ich getäuscht habe, und dies wird die erste Schlussfolgerung sein: Bevor Sie mit der Aufgabe fortfahren, sollten Sie darüber nachdenken - ist es möglich, sie im Voraus irgendwie zu vereinfachen?

Der Vergleichsalgorithmus ist recht einfach: Die Wurzel der Summe der Quadrate der Differenzen der beiden Signaturen wird berechnet, geteilt durch die Summe der zuvor berechneten Werte (d. H. In jeder Iteration wird die Summierung immer noch als Konstante herausgenommen und kann überhaupt nicht als konstant herausgenommen werden) und mit dem Schwellenwert verglichen werden. Es ist anzumerken, dass Signaturelemente auf Werte von -2 bis +2 beschränkt sind und dementsprechend der absolute Wert der Differenz auf Werte von 0 bis 4 begrenzt ist.


Nichts kompliziertes, aber die Menge entscheidet.

Erster Ansatz, naiv

//  const val d = 0.3 // 10.000.000 . //      , //        val collection: MutableList<Signature> = mutableListOf() // signature —   420   Byte class Signature(val signature: Array<Byte>, val norma: Double) fun getSimilar(signature: Signature) = collection .filter { calculateDistance(it, signature) < d } fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> Math.pow((value - second.signature[index]).toDouble(), 2.0) }.sum()) / (first.norma + second.norma) 

Berechnen wir, was wir hier haben, mit der Anzahl der Operationen:

10M Math.sqrt
10M Ergänzungen und Abteilungen / (first.norma + second.norma)
4.200M Subtraktionen und Quadrieren von Math.pow((value - second.signature[index]).toDouble(), 2.0)
4.200M Ergänzungen .sum()

Welche Möglichkeiten haben wir:

1. Bei solchen Volumina ist es eine unverzeihliche Verschwendung, ein ganzes Byte (oder, Gott bewahre, jemand hätte gedacht, Int zu verwenden) zum Speichern von drei signifikanten Bits auszugeben.
2. Vielleicht, wie man den Umfang der Mathematik reduziert?
3. Aber ist es möglich, eine vorläufige Filterung durchzuführen, die nicht so rechenintensiv ist?

Den zweiten Ansatz packen wir

Übrigens, wenn jemand vorschlägt, wie Sie die Berechnungen mit einer solchen Verpackung vereinfachen können, erhalten Sie ein großes Dankeschön und ein Plus an Karma. Obwohl einer, aber von ganzem Herzen :)

One Long ist 64 Bit, in unserem Fall können wir 21 Werte darin speichern (und 1 Bit bleibt ungeklärt).

 //   20   Long class Signature(val signature: Array<Long>, val norma: Double) fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> calculatePartial(value, second.signature[index]) }.sum()) / (first.norma + second.norma) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L (0..60 step 3).onEach { val current = (first.ushr(it) and 0x7) - (second.ushr(it) and 0x7) sum += current * current } return sum.toDouble() } 

Es ist besser aus dem Speicher ( 4.200M gegenüber 1.600M , wenn auch ungefähr), aber was ist mit den Berechnungen?

Ich denke, es ist offensichtlich, dass die Anzahl der Operationen gleich geblieben ist und 8.400M Schichten und 8.400M logische 8.400M hinzugefügt wurden. Vielleicht kann es optimiert werden, aber der Trend ist immer noch nicht glücklich - das ist nicht das, was wir wollten.

Der dritte Ansatz ist das Umpacken mit Sub-Subs

Am Morgen kann ich es riechen, hier kannst du etwas Magie anwenden!

Speichern wir die Werte nicht in drei, sondern in vier Bits. Auf diese Weise:

Ja, wir werden die Packungsdichte im Vergleich zur vorherigen Version verlieren, aber wir werden die Möglichkeit bekommen, Long mit 16 (nicht ganz) Unterschieden mit einem XOR -Ohm auf einmal zu erhalten. Darüber hinaus gibt es nur 11 Optionen für die Verteilung von Bits in jedem endgültigen Halbbyte, sodass Sie vorberechnete Werte der Quadrate der Differenzen verwenden können.

 //   27   Long class Signature(val signature: Array<Long>, val norma: Double) // -1    val precomputed = arrayOf(0, 1, 1, 4, 1, -1, 4, 9, 1, -1, -1, -1, 4, -1, 9, 16) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L val difference = first xor second (0..60 step 4).onEach { sum += precomputed[(difference.ushr(it) and 0xF).toInt()] } return sum.toDouble() } 

Aus dem Speicher wurde es 2.160M gegenüber 1.600M - unangenehm, aber immer noch besser als die anfänglichen 4.200M .

Berechnen wir die Operationen:

10M Quadratwurzeln, Ergänzungen und Unterteilungen (nirgendwo hingegangen)
270M XOR 's
4.320 Hinzufügungen, Verschiebungen, logische 4.320 und Extrakte aus dem Array.

Es sieht schon interessanter aus, aber es gibt trotzdem zu viele Berechnungen. Leider scheinen wir diese 20% der Anstrengungen bereits aufgewendet zu haben, um 80% des Ergebnisses zu erzielen, und es ist Zeit darüber nachzudenken, wo Sie sonst noch profitieren können. Das erste, was mir in den Sinn kommt, ist, es überhaupt nicht zu einer Berechnung zu bringen und offensichtlich unangemessene Signaturen mit einem leichten Filter herauszufiltern.

Vierter Ansatz, großes Sieb

Wenn Sie die Berechnungsformel leicht transformieren, können Sie diese Ungleichung erhalten (je kleiner der berechnete Abstand, desto besser):


Das heißt, Jetzt müssen wir herausfinden, wie der minimal mögliche Wert der linken Seite der Ungleichung basierend auf den Informationen berechnet werden kann, die wir über die Anzahl der in Long gesetzten Bits haben. Dann verwerfen Sie einfach alle Unterschriften, die ihn nicht zufrieden stellen.
Ich möchte Sie daran erinnern, dass x _i Werte von 0 bis 4 annehmen kann (das Vorzeichen ist nicht wichtig, ich denke, es ist klar, warum). Da jeder Term quadratisch ist, lässt sich leicht ein allgemeines Muster ableiten:


Die endgültige Formel sieht so aus (wir werden sie nicht brauchen, aber ich habe sie lange abgeleitet und es wäre eine Schande, sie einfach zu vergessen und niemandem zu zeigen):


Wobei B die Anzahl der gesetzten Bits ist.

Lesen Sie in einem Long nur 64 Bit 64 mögliche Ergebnisse. Und sie werden im Voraus perfekt berechnet und analog zum vorherigen Abschnitt zu einem Array hinzugefügt.

Darüber hinaus ist es völlig optional, alle 27 Longs zu berechnen. Es reicht aus, den Schwellenwert beim nächsten zu überschreiten, und Sie können die Prüfung unterbrechen und false zurückgeben. Der gleiche Ansatz kann übrigens in der Hauptberechnung verwendet werden.

 fun getSimilar(signature: Signature) = collection .asSequence() //     !? .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } val estimateValues = arrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 69, 74, 79, 84, 89, 94, 99, 104, 109, 114, 119, 124, 129, 134, 139, 144, 151, 158, 165, 172, 179, 186, 193, 200, 207, 214, 221, 228, 235, 242, 249, 256) fun estimate(first: Signature, second: Signature):Boolean{ var bitThreshold = Math.pow(d * (first.norma + second.norma), 2.0).toLong() first.signature.forEachIndexed { index, value -> bitThreshold -= estimateValues[java.lang.Long.bitCount(value xor second.signature[index])] if (bitThreshold <= 0) return false } return true } 

Hierbei ist zu verstehen, dass die Wirksamkeit dieses Filters (bis zu negativ) katastrophal von der ausgewählten Schwelle und etwas weniger stark von den Eingabedaten abhängt. Glücklicherweise gelingt es einer relativ kleinen Anzahl von Objekten für den erforderlichen Schwellenwert d=0.3 den Filter zu passieren, und der Beitrag ihrer Berechnung zur Gesamtantwortzeit ist so gering, dass sie vernachlässigt werden können. Und wenn ja, können Sie etwas mehr sparen.

Fünfter Ansatz, Sequenz loswerden

Bei der Arbeit mit großen Sammlungen ist die sequence eine gute Verteidigung gegen die äußerst unangenehmen Speicherausfälle . Wenn wir jedoch offensichtlich wissen, dass die Sammlung beim ersten Filter auf eine vernünftige Größe reduziert wird, wäre es eine viel vernünftigere Wahl, eine gewöhnliche Iteration in einer Schleife mit der Erstellung einer Zwischensammlung zu verwenden, da die sequence nicht nur modisch und jugendlich ist, sondern auch ein Iterator. das hasNext Begleiter, die weit davon entfernt sind, frei zu sein.

 fun getSimilar(signature: Signature) = collection .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } 

Es scheint, dass es hier Glück ist, aber ich wollte es "schön machen". Hier kommen wir zu der versprochenen lehrreichen Geschichte.

Sechster Ansatz, wir wollten das Beste

Wir schreiben über Kotlin und hier einige ausländische java.lang.Long.bitCount ! Und in jüngerer Zeit wurden nicht signierte Typen in die Sprache gebracht. Angriff!

Kaum gesagt als getan. Alle ULong durch ULong ersetzt. ULong aus der Java-Quelle herausgerissen und als Erweiterungsfunktion für ULong

 fun ULong.bitCount(): Int { var i = this i = i - (i.shr(1) and 0x5555555555555555uL) i = (i and 0x3333333333333333uL) + (i.shr(2) and 0x3333333333333333uL) i = i + i.shr(4) and 0x0f0f0f0f0f0f0f0fuL i = i + i.shr(8) i = i + i.shr(16) i = i + i.shr(32) return i.toInt() and 0x7f } 

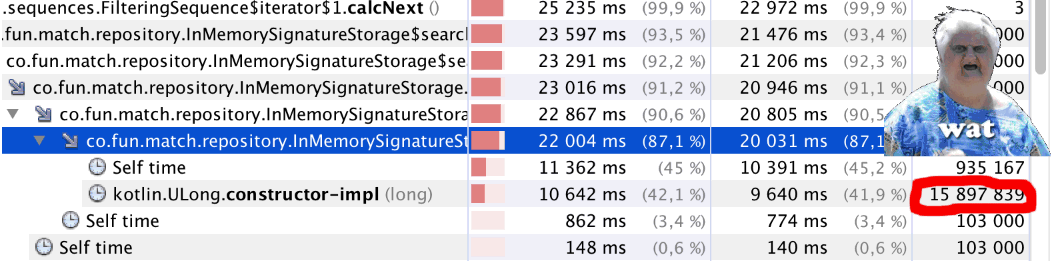
Wir fangen an und ... etwas stimmt nicht. Der Code begann merklich langsamer zu arbeiten. Wir starten den Profiler und sehen etwas Seltsames (siehe bitCount() Artikels): etwas weniger als eine Million Aufrufe von bitCount() fast 16 Millionen Aufrufe von Kotlin.ULong.constructor-impl . WAT !?

Das Rätsel wird einfach erklärt - schauen Sie sich einfach den Klassencode ULong

 public inline class ULong @PublishedApi internal constructor(@PublishedApi internal val data: Long) : Comparable<ULong> { @kotlin.internal.InlineOnly public inline operator fun plus(other: ULong): ULong = ULong(this.data.plus(other.data)) @kotlin.internal.InlineOnly public inline operator fun minus(other: ULong): ULong = ULong(this.data.minus(other.data)) @kotlin.internal.InlineOnly public inline infix fun shl(bitCount: Int): ULong = ULong(data shl bitCount) @kotlin.internal.InlineOnly public inline operator fun inc(): ULong = ULong(data.inc())  .. } 

Nein, ich verstehe alles, ULong ist jetzt experimental , aber wie ist das?
Im Allgemeinen erkennen wir den Ansatz als fehlgeschlagen an, was schade ist.

Nun, aber vielleicht kann noch etwas verbessert werden?

Eigentlich kannst du. Der ursprüngliche Code java.lang.Long.bitCount ist nicht der optimalste. Im allgemeinen Fall ergibt sich ein gutes Ergebnis. Wenn wir jedoch im Voraus wissen, auf welchen Prozessoren unsere Anwendung funktioniert, können wir einen optimaleren Weg wählen. Hier ist ein sehr guter Artikel über Habré. Ich empfehle dringend, einzelne Bits zu zählen . Ich empfehle dringend, ihn zu lesen.

Ich habe die "kombinierte Methode" verwendet

 fun Long.bitCount(): Int { var n = this n -= (n.shr(1)) and 0x5555555555555555L n = ((n.shr(2)) and 0x3333333333333333L) + (n and 0x3333333333333333L) n = ((((n.shr(4)) + n) and 0x0F0F0F0F0F0F0F0FL) * 0x0101010101010101).shr(56) return n.toInt() and 0x7F } 

Papageien zählen

Alle Messungen wurden willkürlich während der Entwicklung auf dem lokalen Computer durchgeführt und aus dem Speicher reproduziert. Daher ist es schwierig, über die Genauigkeit zu sprechen, aber Sie können den ungefähren Beitrag jedes Ansatzes abschätzen.

Schlussfolgerungen

• Bei der Verarbeitung großer Datenmengen lohnt es sich, Zeit für eine vorläufige Analyse aufzuwenden. Möglicherweise müssen nicht alle diese Daten verarbeitet werden.
• Wenn Sie eine grobe, aber billige Vorfilterung verwenden können, kann dies sehr hilfreich sein.
• Ein bisschen Magie ist unser Alles. Gegebenenfalls natürlich.
• Das Betrachten von Quellcodes von Standardklassen und -funktionen ist manchmal sehr nützlich.

Vielen Dank für Ihre Aufmerksamkeit! :) :)

Und ja, um fortzufahren.