Um eine Nachricht von einer Basisstation an ein mobiles Gerät zu übertragen (und umgekehrt), muss eine elektromagnetische Welle eine erhebliche Anzahl von Hindernissen überwinden: Reflexion, Brechung, Streuung, Abschattung, Doppler-Frequenzverschiebungen usw. Erstens werden alle diese Effekte nach dem mathematischen Modell solcher Effekte als multiplikativ (aus dem Englischen. Multiplikation - Multiplikation) bezeichnet. Und zweitens kann es unter dem allgemeinen Begriff des Verblassens gesammelt werden.
Von Standard zu Standard, von Generation zu Generation, von Technologie zu Technologie haben Wissenschaftler und Ingenieure Probleme mit dem Problem der Nivellierung dieser Fading (Fading Mitigation).
Und einige Lösungen sind weit verbreitet. Sagen wir mehr: Fast alle von ihnen sind auf die eine oder andere Weise mit dem Konzept der Vielfalt verbunden .

Die Quelle der Illustration (nein, dies ist keine Werbung, nur eine erfolgreiche Kombination des gewünschten Begriffs und der Katze).
Ein Beispiel für solche Lösungen:
- Frequenzsprung - gegen frequenzselektives Fading;
- Kanalschätzung und -entzerrung durch Rückkopplung - GSM, um Änderungen im Zeitbereich zu unterdrücken;
- Spectrum Extension (UMTS);
- Pilotsignale (beginnend mit UMTS) auf dem Downlink (Downlink) und Signalverfolgung (Signalverfolgung) auf dem Uplink (Uplink) - um Änderungen im Zeitbereich zu unterdrücken;
- OFDM - LTE gegen frequenzselektives Fading;
- Zeitliche Diversität ( fehlerkorrigierende Codierung );
- Polarisationsdiversität (auf der Senderseite) + Addierer (Kombinierer auf der Empfängerseite);
- Räumliche Vielfalt .
Die letzte dieser Techniken werden wir heute als Teil eines anderen Themas zu MIMO betrachten .
Raumdiversitätsreihenfolge und Arraygewinn
Der erste.
Es gibt ein solches Konzept - die Reihenfolge der Raumdiversität: Wenn dieselben Informationen aus verschiedenen Richtungen gesammelt werden können, steigt die Hoffnung, sie wiederherzustellen. Als Beispiel aus dem Leben können wir uns vorstellen, Informationen über dasselbe Ereignis aus unabhängigen Informationsquellen zu sammeln. In der Funkkommunikation können wir diese Reihenfolge erhöhen, auch durch Verwendung von MISO , SIMO oder MIMO .
Die theoretische Grenze einer solchen Vielfalt  wo
wo  - die Anzahl der Sendeantennen und
- die Anzahl der Sendeantennen und  - die Anzahl der Empfangsantennen. Denken Sie daran.
- die Anzahl der Empfangsantennen. Denken Sie daran.
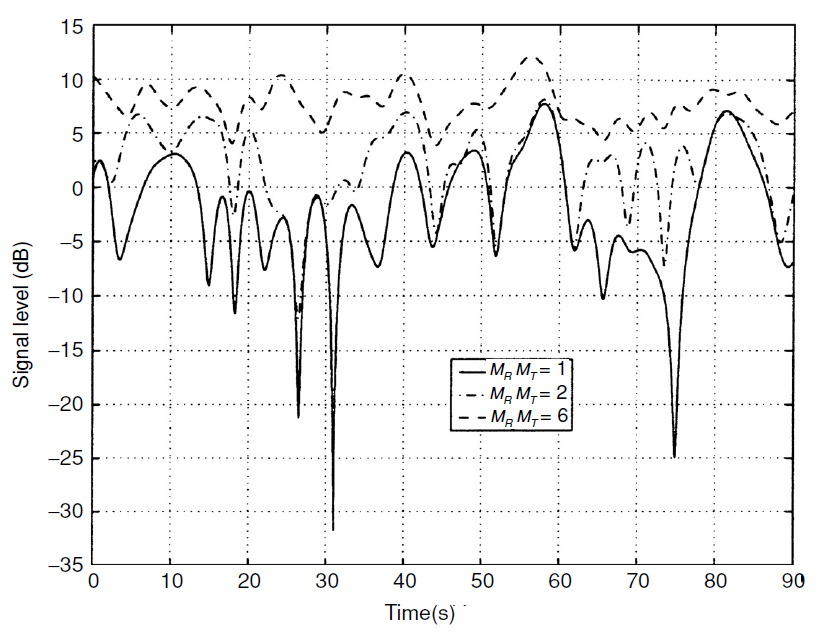
Abb. 1. Kanalstabilität durch Erhöhung der räumlichen Diversitätsordnung. Bei Werten  Der Kanal ist vollständig stabilisiert und verwandelt sich in einen Kanal ohne Fading (AWGN) [1, S. 101] .
Der Kanal ist vollständig stabilisiert und verwandelt sich in einen Kanal ohne Fading (AWGN) [1, S. 101] .
Der zweite.
Mit SIMO , MIMO und sogar MISO (im Fall eines bekannten Kanals) kann man die sogenannte Array-Verstärkung erhalten . Dies bedeutet, dass die Verwendung mehrerer Empfangsantennen und / oder die korrekte Energieverteilung auf der Sendeseite das Signal-Rausch-Verhältnis (SNR) erhöhen und somit die Anzahl der Fehler verringern kann.
Die Ordnungen der Diversität und des Array-Gewinns für verschiedene Konfigurationen können analytisch abgeleitet werden [1, S. 86 - 100] und auf eine Tabelle reduzieren [1, p. 101] sowohl für den Fall, dass der Kanal unbekannt ist (CU - Channel Unknown) als auch für den Fall, dass der Kanal auf der Seite des Senders bekannt ist (CK - Channel Unown).
Okay, auch bei großen Strichen, aber jetzt haben wir zumindest ein gewisses Verständnis für die theoretischen Aspekte der Unterdrückung des Verblassens. Die nächste Frage ist, wie diese theoretischen Grenzen erreicht werden können. Was sind die Techniken zur Aktivierung der betrachteten Gewinne?
Lösung Nr. 1. Raum-Zeit-Codes
Eine der beliebtesten Klassen von Lösungen für räumliche Vielfalt ist möglicherweise die Klasse der Raum-Zeit-Codes (Raum-Zeit-Codes). Zum Beispiel die bekannte, glaube ich, viele Alamouti-Methode (ein Beispiel für Blockcode) [2, S. 40-46]:
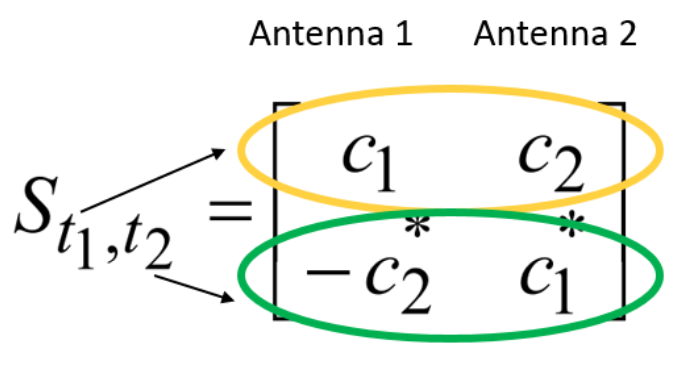
wo  bei
bei  Sind einige Eingabezeichen
Sind einige Eingabezeichen  bei
bei  Sind Zeitfenster und
Sind Zeitfenster und  - Dies ist in der Tat eine Codierungsmatrix.
- Dies ist in der Tat eine Codierungsmatrix.
Das Alamouti-Schema ist orthogonal [1, S. 93-95, 97-98] und erfordert vor allem keine Kanalstatusinformationen.
Die mathematische Beschreibung der Übertragung des vom Alamouti-Schema codierten Signals sowie einige Beispiele für die Modellierung dieser Technik in MatLab finden Sie in meinem Repository . Interessiert an Willkommen!
Wie Sie jedoch sehen können, ist die Alamouti-Schaltung ein Fall, in dem wir nur zwei Sendeantennen haben (  )
)
Aber verlieren Sie nicht den Mut im Voraus: Natürlich gibt es auch andere Möglichkeiten, sie werden einfach etwas anders genannt. Beispielsweise kann man gemäß [3] die folgenden Codierungsschemata anwenden:
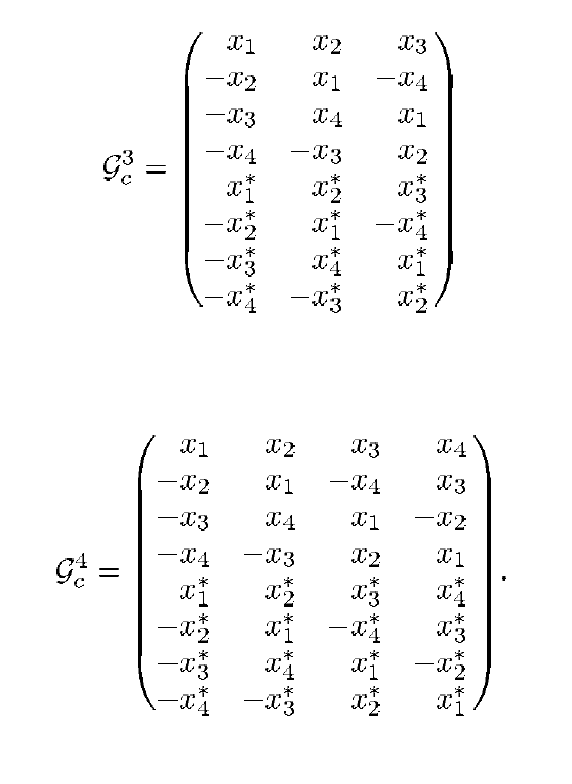
Abb. 2. Übertragungsschemata für Fälle  und
und  [2].
[2].
Und es gibt viele andere Möglichkeiten: Nur um die Bedingungen der Orthogonalität zu erfüllen.
Solche Codes erfordern tatsächlich die gleichen Verfahren zum Codieren und Decodieren wie für den Alamouti-Code. Daher werden sie normalerweise unter dem allgemeinen Begriff orthogonale Raum-Zeit-Blockcodes (OSTBC - Ortogonale Raum-Zeit-Blockcodes) kombiniert.
Diese Codeklasse wird in den Materialien "Einführung in MIMO-Systeme" von MathWorks besonders berücksichtigt. Ich rate allen Interessierten dringend, es zu lesen!
Was ist der Preis?
Wie aus dem Übertragungsschema ersichtlich ist, verbringen wir, obwohl wir Symbole parallel übertragen, mehrere Zeitschlitze damit. Daher opfern wir die Bandbreite (zumindest bekommen wir sie weniger). Für das Alamouti-Schema ist ein solcher Kompromiss symmetrisch: Wir verwenden 2 Antennen und 2 Zeitschlitze (als ob SISO in Bezug auf die Bandbreite verwendet würde). Andere Schemata können die Übertragungsgeschwindigkeit noch stärker beeinflussen.
Entscheidung Nr. 2. DET: Dominante Eigenmodusübertragung
Nun, für die vorherige Klasse von Techniken war die Kenntnis des Kanals für uns nicht wichtig. Aber was ist, wenn wir dieses Wissen noch haben? Gibt es in diesem Fall geeignetere Techniken?
In einem meiner vorherigen Artikel haben wir besprochen, dass wir, wenn wir den Zustand des Kanals kennen, verschiedene Methoden der Signalverarbeitung anwenden können, um den Durchsatz zu erhöhen. Das gleiche Prinzip erhöht die Störfestigkeit.
Wahrscheinlich haben viele von der MRC- Methode gehört und viele wissen, dass diese Methode für den SIMO- Fall sehr gut geeignet ist, wenn mindestens eine Antenne in der Übertragung vorhanden ist, aber es gibt immer noch viele davon, was bedeutet, dass es etwas zu kombinieren gibt.
Aber wahrscheinlich stieß bereits eine geringere Anzahl von Lesern auf MRC auf der Sendeseite (Tx-MRC) [1, S. 95,96] und noch weniger mit DET- Technologie (Dominant Eigenmode Transmission) [1, p. 98-100]. Repariere es!
Betrachten Sie zunächst den allgemeinen Fall des MIMO-Kanals und die letzte dieser Methoden - DET.
Was ist die Essenz von:
- Wenn der Sender eine Matrix hat
 dann kann es verarbeitet werden.
dann kann es verarbeitet werden. - Zerlegen Sie es beispielsweise über SVD :
 So erhalten Sie mehrere Matrizen einer bestimmten Eigenschaft.
So erhalten Sie mehrere Matrizen einer bestimmten Eigenschaft. - Diese Eigenschaften können verwendet werden, um die Übertragung zu optimieren, beispielsweise durch Vorcodierung (Vorcodierung).
Wir führen einige vorcodierende Vektoren ein:
wo  Ist der erste (sozusagen dominante) Matrixvektor
Ist der erste (sozusagen dominante) Matrixvektor  .
.
Darüber hinaus können wir auch den Nachbearbeitungsvektor schreiben:
wo  Ist der erste Vektor der Matrix
Ist der erste Vektor der Matrix  .
.
Definieren Sie das Modell des empfangenen Signals neu (siehe Thema Bandbreite ):
Voila! Die Magie der linearen Algebra hat unter allen Verteilungspfaden die profitabelsten herausgegriffen und die gesamte Energie dorthin gelenkt. Tatsächlich haben wir einen linearen Strahlformungsalgorithmus vor uns.
Auf Kosten dieses Ansatzes erfolgt, genau wie im Fall von OSTBC, eine Bandbreitenbeschränkung. Dies geschieht zwar nur im räumlichen Bereich.
Warum enthält die Methode Eigenwerte in ihrem Namen, wenn es sich nur um singuläre Werte handelt?Weil die Eigenwerte (Kardinalität der Ausbreitungswege - Fading) direkt aus Singularzahlen (Fading-Amplituden) abgeleitet werden können:
Nun, mit DET ist mehr oder weniger klar, was mit Tx-MRC ist.
Bei ihm ist es noch einfacher - dies ist ein Sonderfall von DET, und jetzt werden wir es beweisen.
Für Tx-MRC wird in der Literatur der folgende vorcodierende Vektor vorgeschlagen:
Wir denken daran, dass das Quadrat der Frobenius-Norm gleich dem Eigenwert und dementsprechend dem Quadrat der Singularzahl ist  (im Fall von SIMO und MISO).
(im Fall von SIMO und MISO).
Andererseits definieren wir das Modell des empfangenen Signals nur für den MISO-Fall neu:
Welches musste beweisen.
Beachten Sie, dass wir jetzt nicht nur über die Trennung von Signalen auf der Sendeseite und deren Kombination auf der Empfangsseite sprechen, wie dies bei OSTBC der Fall war. Jetzt geht es um die optimale Energieverteilung. Dies bedeutet, dass die Werte der Array-Verstärkung in diesem Fall höher sind als die von OSTBC.
Nachdem alle Wörter gesprochen wurden, werden wir versuchen, unsere Techniken zu simulieren.
Modellierung
Heute habe ich ein wenig gezählt: Für die OSTBC- Modellierung wurden vorgefertigte Objekte aus der Communication Toolbox verwendet (MatLab R2014a - welches es war):
Für die Modulation und Demodulation (und Bitfehlerberechnung - BER) wurden keine Funktionen mehr verwendet, sondern Funktionen . Ihre Analoga sind im Kommunikations- Octave-Paket enthalten.
Quellcodes finden Sie hier.clear all; close all; clc snapshots = 100000; EbNo = 0:15; M = 2;
Es sollte sich ungefähr so herausstellen:
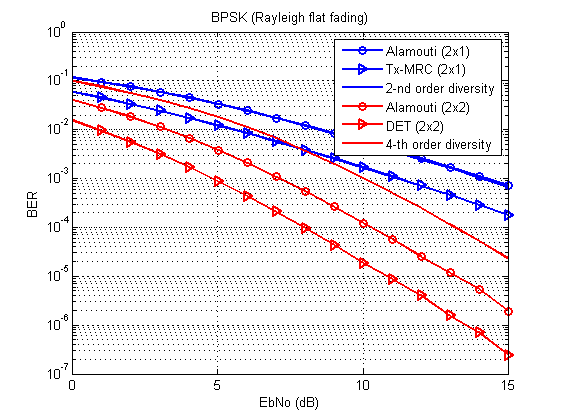
Abb. 3. Bit- / Symbolfehlerkurven für verschiedene Übertragungstechniken (BPSK, Rayleigh-Kanal mit flachem Fading). Vergleiche mit [1, S. 96, 100].
Und jetzt ist die Frage: Wo ist die Kurve der theoretischen Grenze der Diversität zweiter Ordnung?
Die AntwortAlles entspricht der Tabelle: Diese Kurve stimmt vollständig mit dem Alamouti 2x1 überein. Bei MIMO kommt auch die Array-Verstärkung ins Spiel, sodass die Kurven getrennt werden.
Auf die eine oder andere Weise wird erwartet, dass DET (oder Tx-MRC) Alamouti in seiner Qualität übertrifft.
So: Wissen ist Macht!
Literatur
Paulraj, Arogyaswami, Rohit Nabar und Dhananjay Gore. Einführung in die drahtlose Raum-Zeit-Kommunikation. Cambridge University Press, 2003.
Bakulin M. G., Varukina L. A., Kreindelin V. B. MIMO-Technologie: Prinzipien und Algorithmen // M .: Hotline - Telecom. - 2014 - T. 244.
Tarokh, V., Jafarkhani, H. & Calderbank, AR (1999). Raum-Zeit-Blockcodes aus orthogonalen Designs. IEEE Transactions on Information Theory, 45 (5), 1456-1467.
PS
Dem Lehrpersonal und der Studentengemeinschaft meines Heimatberufs sage ich Hallo!