Einführung in das maschinelle Lernen

Den vollständigen Kurs in Russisch finden Sie unter diesem Link .
Der ursprüngliche Englischkurs ist unter diesem Link verfügbar.



Alle 2-3 Tage sind neue Vorträge geplant.

Interview mit Sebastian Trun, CEO Udacity

"Hallo nochmal, ich bin Paige und du bist heute mein Gast, Sebastian."
- Hallo, ich bin Sebastian!
- ... ein Mann, der eine unglaubliche Karriere hat, der es geschafft hat, viele erstaunliche Dinge zu tun! Sie sind Mitbegründer von Udacity, haben Google X gegründet und sind Professor an der Stanford University. Sie haben während Ihrer gesamten Karriere unglaubliche Forschung betrieben und tiefgreifend gelernt. Was hat Sie am meisten befriedigt und in welchem ​​Bereich haben Sie die meisten Belohnungen für die geleistete Arbeit erhalten?
- Ehrlich gesagt, ich liebe es wirklich, im Silicon Valley zu sein! Ich mag es, in der Nähe von Menschen zu sein, die viel schlauer sind als ich, und ich habe Technologie immer als ein Werkzeug angesehen, das die Spielregeln auf verschiedene Weise ändert - von Bildung über Logistik bis hin zu Gesundheitswesen usw. All dies ändert sich so schnell und es besteht ein unglaublicher Wunsch, an diesen Veränderungen teilzunehmen und sie zu beobachten. Sie schauen auf Ihre Umgebung und verstehen, dass das meiste, was Sie um sich herum sehen, nicht so funktioniert, wie es sollte - Sie können immer etwas Neues erfinden!
- Nun, das ist eine sehr optimistische Sicht der Technologie! Was war die größte Eureka während Ihrer Karriere?
- Herr, es gab so viele! Ich erinnere mich an einen Tag, an dem Larry Page mich anrief und vorschlug, Autopilot-Autos zu bauen, die durch alle Straßen Kaliforniens fahren könnten. Zu dieser Zeit galt ich als Experte, ich wurde zu diesen gezählt und ich war genau die Person, die sagte: "Nein, das geht nicht." Danach hat Larry mich überzeugt, dass es im Prinzip möglich ist, dies zu tun, man muss nur anfangen und es versuchen. Und wir haben es geschafft! Dies war der Moment, in dem mir klar wurde, dass selbst Experten falsch liegen und „Nein“ sagen, wir sind 100% pessimistisch. Ich denke, wir sollten offener für das Neue sein.
- Oder wenn Larry Page Sie anruft und sagt: "Hey, mach eine coole Sache wie Google X" und du bekommst etwas ziemlich Cooles!
- Ja, das ist sicher, Sie müssen sich nicht beschweren! Ich meine, all dies ist ein Prozess, der auf dem Weg zur Implementierung viel diskutiert wird. Ich habe großes Glück zu arbeiten und bin stolz darauf, bei Google X und bei anderen Projekten.
- Super! In diesem Kurs geht es also nur um die Arbeit mit TensorFlow. Haben Sie Erfahrung mit TensorFlow oder sind Sie damit vertraut (gehört)?
- Ja! Ich liebe TensorFlow buchstäblich! In meinem eigenen Labor verwenden wir es oft und häufig. Eines der bedeutendsten Werke, das auf TensorFlow basiert, wurde vor etwa zwei Jahren veröffentlicht. Wir haben gelernt, dass iPhone und Android Hautkrebs wirksamer erkennen können als die besten Dermatologen der Welt. Wir haben unsere Forschungen in Nature veröffentlicht und dies hat zu einer Art Aufregung in der Medizin geführt.
- Das klingt großartig! Sie kennen und lieben TensorFlow, das an sich großartig ist! Haben Sie bereits mit TensorFlow 2.0 gearbeitet?
- Nein, leider hatte ich noch keine Zeit.
- Er wird einfach unglaublich sein! Alle Teilnehmer dieses Kurses arbeiten mit dieser Version.
- Ich beneide sie! Ich werde es auf jeden Fall versuchen!
- Großartig! In unserem Kurs gibt es viele Studenten, die sich in ihrem Leben noch nie mit maschinellem Lernen beschäftigt haben, vom Wort "vollständig". Für sie kann das Feld neu sein, vielleicht ist es für jemanden, der selbst programmiert, neu. Welchen Rat hast du für sie?
- Ich möchte, dass sie offen bleiben - für neue Ideen, Techniken, Lösungen, Positionen. Maschinelles Lernen ist eigentlich einfacher als Programmieren. Bei der Programmierung müssen Sie jeden Fall in den Quelldaten berücksichtigen, die Programmlogik und die Regeln dafür anpassen. Zu diesem Zeitpunkt trainieren Sie den Computer mithilfe von TensorFlow und maschinellem Lernen im Wesentlichen anhand von Beispielen, sodass der Computer die Regeln selbst finden kann.
- Das ist unglaublich interessant! Ich kann es kaum erwarten, den Studenten in diesem Kurs etwas mehr über maschinelles Lernen zu erzählen! Sebastian, danke, dass du dir die Zeit genommen hast, heute zu uns zu kommen!
- Danke! Bleib in Kontakt!

Was ist maschinelles Lernen?

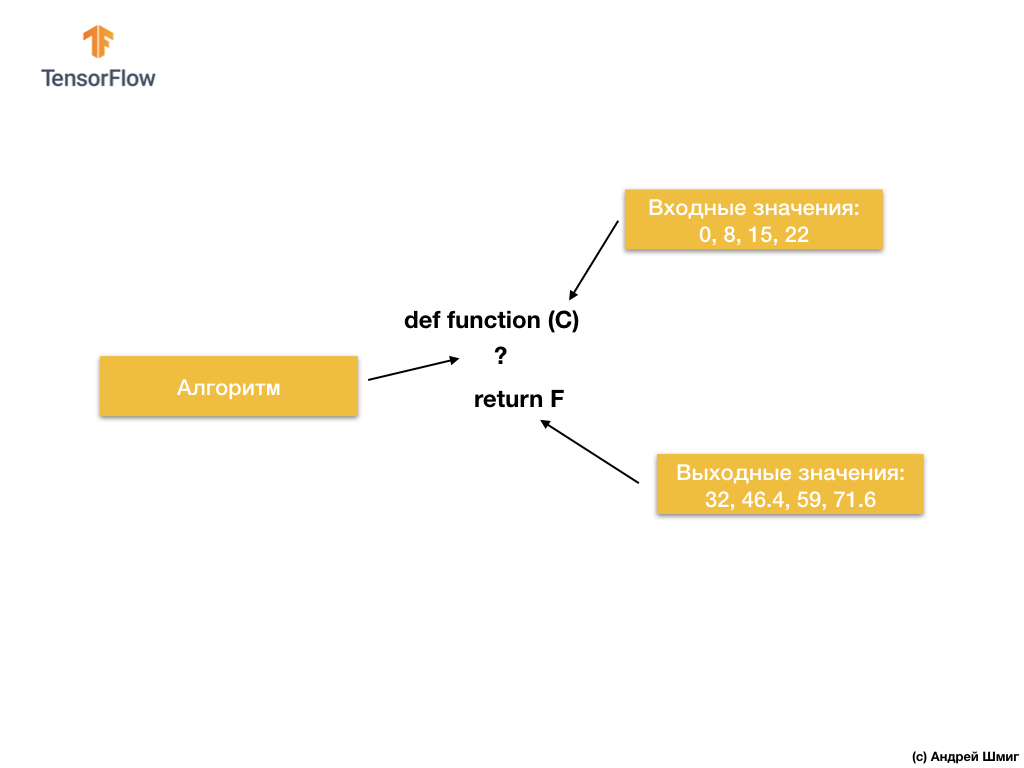
Beginnen wir also mit der folgenden Aufgabe - gegebenen Eingabe- und Ausgabewerten.



Wenn Sie den Wert 0 als Eingabewert haben, dann 32 als Ausgabewert. Wenn Sie 8 als Eingabewert haben, dann 46,4 als Ausgabewert. Wenn Sie 15 als Eingabewert haben, dann 59 als Ausgabewert und so weiter.

Schauen Sie sich diese Werte genauer an und lassen Sie mich eine Frage stellen. Können Sie bestimmen, wie die Ausgabe aussehen wird, wenn wir am Eingang 38 erhalten?



Wenn Sie mit 100.4 geantwortet haben, hatten Sie Recht!



Wie können wir dieses Problem lösen? Wenn Sie sich die Werte genau ansehen, können Sie sehen, dass sie durch den Ausdruck zusammenhängen:



Wobei C - Grad Celsius (Eingabewerte), F - Fahrenheit (Ausgabewerte).

Was Ihr Gehirn gerade getan hat - Eingabewerte und Ausgabewerte verglichen und ein gemeinsames Modell (Verbindung, Abhängigkeit) zwischen ihnen gefunden - ist das, was maschinelles Lernen tut.

Basierend auf den Eingabe- und Ausgabewerten finden Algorithmen für maschinelles Lernen einen geeigneten Algorithmus zum Konvertieren von Eingabewerten in Ausgabewerte. Dies kann wie folgt dargestellt werden:



Schauen wir uns ein Beispiel an. Stellen Sie sich vor, wir möchten ein Programm entwickeln, das Grad Celsius in Grad Fahrenheit mit der Formel F = C * 1.8 + 32 umwandelt.



Die Lösung kann aus Sicht der traditionellen Softwareentwicklung in jeder Programmiersprache mit der folgenden Funktion implementiert werden:



Was haben wir also? Die Funktion nimmt einen Eingabewert von C an, berechnet dann den Ausgabewert von F unter Verwendung eines expliziten Algorithmus und gibt dann den berechneten Wert zurück.



Andererseits haben wir beim Ansatz des maschinellen Lernens nur Eingabe- und Ausgabewerte, nicht aber den Algorithmus selbst:



Der Ansatz des maschinellen Lernens beruht auf der Verwendung neuronaler Netze, um die Beziehung zwischen Eingabe- und Ausgabewerten zu finden.



Sie können sich neuronale Netze als einen Stapel von Schichten vorstellen, von denen jede aus zuvor bekannten mathematischen (Formeln) und internen Variablen besteht. Der Eingabewert tritt in das neuronale Netzwerk ein und durchläuft einen Stapel von Schichten von Neuronen. Beim Durchlaufen der Ebenen wird der Eingabewert gemäß der Mathematik (vorgegebene Formeln) und den Werten der internen Variablen der Ebenen konvertiert, wodurch ein Ausgabewert erzeugt wird.

Damit das neuronale Netzwerk die richtige Beziehung zwischen den Eingabe- und Ausgabewerten lernen und bestimmen kann, müssen wir es trainieren - trainieren.

Wir trainieren das neuronale Netzwerk durch wiederholte Versuche, Eingabewerte mit Ausgabewerten abzugleichen.



Während des Trainings erfolgt die „Anpassung“ (Auswahl) der Werte interner Variablen in den Schichten des neuronalen Netzwerks, bis das Netzwerk lernt, die entsprechenden Ausgabewerte zu den entsprechenden Eingabewerten zu generieren.

Wie wir später sehen werden, werden Tausende oder Zehntausende von Iterationen (Trainings) durchgeführt, um ein neuronales Netzwerk zu trainieren und es in die Lage zu versetzen, die am besten geeigneten Werte für interne Variablen auszuwählen.



Als vereinfachte Version des Verständnisses des maschinellen Lernens können Sie sich Algorithmen für maschinelles Lernen als Funktionen vorstellen, die die Werte interner Variablen so auswählen, dass die richtigen Eingabewerte den korrekten Ausgabewerten entsprechen.

Es gibt viele Arten von neuronalen Netzwerkarchitekturen. Unabhängig davon, für welche Architektur Sie sich entscheiden, bleibt die Mathematik im Inneren (welche Berechnungen werden in welcher Reihenfolge durchgeführt) während des Trainings unverändert. Anstatt die Mathematik zu ändern, ändern sich die internen Variablen (Gewichte und Offsets) während des Trainings.

Bei der Umrechnung von Grad Celsius in Fahrenheit beginnt das Modell beispielsweise damit, den Eingabewert mit einer bestimmten Zahl (Gewicht) zu multiplizieren und einen weiteren Wert (Offset) hinzuzufügen. Das Modelltraining besteht darin, geeignete Werte für diese Variablen zu finden, ohne die durchgeführten Multiplikations- und Additionsoperationen zu ändern.

Aber eine coole Sache zum Nachdenken! Wenn Sie das Problem der Umrechnung von Grad Celsius in Fahrenheit gelöst haben, das im Video und im folgenden Text angegeben ist, haben Sie es wahrscheinlich gelöst, weil Sie bereits Erfahrung oder Kenntnisse darüber hatten, wie diese Art der Umrechnung von Grad Celsius in Fahrenheit durchgeführt wird. Zum Beispiel wissen Sie vielleicht nur, dass 0 Grad Celsius 32 Grad Fahrenheit entsprechen. Auf der anderen Seite verfügen Systeme, die auf maschinellem Lernen basieren, nicht über unterstützende Vorkenntnisse, um das Problem zu lösen. Sie lernen, solche Probleme nicht auf der Grundlage von Vorkenntnissen und in ihrer völligen Abwesenheit zu lösen.

Genug geredet - fahren Sie mit dem praktischen Teil der Vorlesung fort!

CoLab: Konvertieren Sie Grad Celsius in Grad Fahrenheit

Die russische Version des CoLab-Quellcodes und die englische Version des CoLab-Quellcodes .

Die Grundlagen: das erste Modell lernen

Willkommen bei CoLab, wo wir unser erstes Modell für maschinelles Lernen trainieren werden!

Wir werden versuchen, die Einfachheit des vorgestellten Materials beizubehalten und nur die für die Arbeit erforderlichen Grundkonzepte einzuführen. Nachfolgende CoLabs enthalten fortgeschrittenere Techniken.

Die Aufgabe, die wir lösen werden, ist die Umrechnung von Grad Celsius in Grad Fahrenheit. Die Umrechnungsformel lautet wie folgt:

$$

$$f = c \ mal 1,8 + 32$$

Natürlich wäre es einfacher, einfach eine Konvertierungsfunktion in Python oder einer anderen Programmiersprache zu schreiben, die direkte Berechnungen durchführen würde, aber in diesem Fall wäre es kein maschinelles Lernen :)

Stattdessen geben wir in die TensorFlow-Eingabe die Eingabegrade von Celsius (0, 8, 15, 22, 38) und die entsprechenden Fahrenheit-Grade (32, 46, 59, 72, 100) ein. Dann werden wir das Modell so trainieren, dass es ungefähr der obigen Formel entspricht.

Abhängigkeiten importieren

Das erste, was wir importieren, ist TensorFlow . Hier und im Folgenden nennen wir es kurz tf . Wir konfigurieren auch die Protokollierungsstufe - nur Fehler.

Als nächstes importieren Sie NumPy als np . Numpy hilft uns, unsere Daten als Hochleistungslisten Numpy .

 from __future__ import absolute_import, division, print_function, unicode_literals import tensorflow as tf tf.logging.set_verbosity(tf.logging.ERROR) import numpy as np 

Vorbereitung der Trainingsdaten

Wie wir bereits gesehen haben, basiert die maschinelle Lerntechnik mit dem Lehrer auf der Suche nach einem Algorithmus zum Konvertieren von Eingabedaten in Ausgaben. Da die Aufgabe dieses CoLab darin besteht, ein Modell zu erstellen, das das Ergebnis der Umrechnung von Grad Celsius in Grad Fahrenheit erzeugen kann, erstellen wir zwei Listen - celsius_q und fahrenheit_a , die wir beim Training unseres Modells verwenden.

 celsius_q = np.array([-40, -10, 0, 8, 15, 22, 38], dtype=float) fahrenheit_a = np.array([-40, 14, 32, 46, 59, 72, 100], dtype=float) for i,c in enumerate(celsius_q): print("{}   = {}  ".format(c, fahrenheit_a[i])) 

-40.0 = -40.0
-10.0 = 14.0
0.0 = 32.0
8.0 = 46.0
15.0 = 59.0
22.0 = 72.0
38.0 = 100.0

Einige Terminologie für maschinelles Lernen:

• Eigenschaft ist der Eingabewert (die Eingabewerte) unseres Modells. In diesem Fall beträgt der Einheitswert Grad Celsius.
• Beschriftungen sind die Ausgabewerte, die unser Modell vorhersagt. In diesem Fall beträgt der Einheitswert Grad Fahrenheit.
• Ein Beispiel ist ein Paar von Eingabe-Ausgabe-Werten, die für das Training verwendet werden. In diesem Fall ist dies ein Wertepaar aus celsius_q und fahrenheit_a unter einem bestimmten Index, z. B. (22,72).

Erstellen Sie ein Modell

Als nächstes erstellen wir ein Modell. Wir werden das einfachste Modell verwenden - das Modell eines vollständig verbundenen Netzwerks ( Dense Netzwerk). Da die Aufgabe ziemlich trivial ist, besteht das Netzwerk auch aus einer einzelnen Schicht mit einem einzelnen Neuron.

Aufbau eines Netzwerks

Wir werden die Ebene l0 ( l ayer und zero) tf.keras.layers.Dense und sie erstellen, indem tf.keras.layers.Dense mit den folgenden Parametern initialisieren:

• input_shape=[1] - Dieser Parameter bestimmt die Dimension des Eingabeparameters - ein einzelner Wert. 1 × 1 Matrix mit einem einzelnen Wert. Da dies die erste (und einzige) Schicht ist, entspricht die Dimension der Eingabedaten der Dimension des gesamten Modells. Der einzige Wert ist ein Gleitkommawert, der Grad Celsius darstellt.
• units=1 - Dieser Parameter bestimmt die Anzahl der Neuronen in der Schicht. Die Anzahl der Neuronen bestimmt, wie viele interne Schichtvariablen für das Training verwendet werden, um eine Lösung für das Problem zu finden. Da dies die letzte Ebene ist, entspricht ihre Dimension der Dimension des Ergebnisses - dem Ausgabewert des Modells - einer einzelnen Gleitkommazahl, die Grad Fahrenheit darstellt. (In einem mehrschichtigen Netzwerk müssen Größe und Form der input_shape mit der Größe und Form der nächsten Ebene übereinstimmen.)

 l0 = tf.keras.layers.Dense(units=1, input_shape=[1]) 

Ebenen in Modell konvertieren

Sobald Ebenen definiert sind, müssen sie in ein Modell konvertiert werden. Sequential Modell verwendet als Argumente die Liste der Ebenen in der Reihenfolge, in der sie angewendet werden müssen - vom Eingabewert bis zum Ausgabewert.

Unser Modell hat nur eine Schicht - l0 .

 model = tf.keras.Sequential([l0]) 

Hinweis
Sehr oft werden Sie auf die Definition von Ebenen direkt in der Modellfunktion stoßen und nicht auf deren vorläufige Beschreibung und anschließende Verwendung:

 model = tf.keras.Sequential([ tf.keras.layers.Dense(units=1, input_shape=[1]) ]) 

Wir kompilieren ein Modell mit einer Verlust- und Optimierungsfunktion

Vor dem Training muss das Modell zusammengestellt (zusammengebaut) werden. Wenn Sie für das Training kompilieren, benötigen Sie:

• Verlustfunktion - eine Methode zum Messen, wie weit der vorhergesagte Wert vom gewünschten Ausgabewert entfernt ist (eine messbare Differenz wird als „Verlust“ bezeichnet).
• Optimierungsfunktion - eine Möglichkeit, interne Variablen anzupassen, um Verluste zu reduzieren.

 model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) 

Die Verlustfunktion und die Optimierungsfunktion werden während des Modelltrainings ( model.fit(...) unten erwähnt) verwendet, um an jedem Punkt erste Berechnungen durchzuführen und dann die Werte zu optimieren.

Die Berechnung der aktuellen Verluste und die anschließende Verbesserung dieser Werte im Modell ist genau das, was Training ist (eine Iteration).

Während des Trainings werden mit der Optimierungsfunktion Anpassungen der Werte interner Variablen berechnet. Ziel ist es, die Werte interner Variablen im Modell so anzupassen (und dies ist in der Tat eine mathematische Funktion), dass sie den vorhandenen Ausdruck für die Umrechnung von Grad Celsius in Grad Fahrenheit so genau wie möglich widerspiegeln.

TensorFlow verwendet numerische Analysen, um diese Art von Optimierungsvorgängen durchzuführen, und all diese Komplexität ist unseren Augen verborgen, sodass wir in diesem Kurs nicht auf Details eingehen werden.

Was ist nützlich, um über diese Optionen zu wissen:

Die in diesem Beispiel verwendete Verlustfunktion (Standardfehler) und Optimierungsfunktion (Adam) sind Standard für solche einfachen Modelle, aber viele andere sind neben ihnen verfügbar. Derzeit ist es uns egal, wie diese Funktionen funktionieren.

Was Sie beachten sollten, ist die Optimierungsfunktion und der Parameter ist der learning rate , der in unserem Beispiel 0.1 beträgt. Dies ist die verwendete Schrittgröße beim Anpassen der internen Werte von Variablen. Wenn der Wert zu klein ist, sind zu viele Trainingsiterationen erforderlich, um das Modell zu trainieren. Zu viel - Genauigkeit sinkt. Das Finden eines guten Wertes für den Lernratenkoeffizienten erfordert einige Versuche und Irrtümer, der normalerweise im Bereich von 0.01 (standardmäßig) bis 0.1 .

Wir trainieren das Modell

Das Training des Modells erfolgt nach der fit Methode.

Während des Trainings empfängt das Modell am Eingang Grad Celsius, führt Transformationen unter Verwendung der Werte interner Variablen (als „Gewichte“ bezeichnet) durch und gibt Werte zurück, die Grad Fahrenheit entsprechen müssen. Da die Anfangswerte der Gewichte willkürlich festgelegt werden, sind die resultierenden Werte weit von den korrekten Werten entfernt. Die Differenz zwischen dem gewünschten und dem tatsächlichen Ergebnis wird mithilfe der Verlustfunktion berechnet, und die Optimierungsfunktion bestimmt, wie die Gewichte angepasst werden sollen.

Dieser Zyklus von Berechnungen, Vergleichen und Anpassungen wird innerhalb der Anpassungsmethode gesteuert. Das erste Argument ist der Eingabewert, das zweite Argument ist der gewünschte Ausgabewert. Das Argument der epochs bestimmt, wie oft dieser Trainingszyklus abgeschlossen werden soll. Das verbose Argument steuert die Protokollierungsstufe.

 history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) print("  ") 

In den folgenden Videos werden wir uns mit den Details befassen, wie dies alles funktioniert und wie genau die vollständig verbundenen Schichten ( Dense Schichten) "unter der Haube" sind.

Trainingsstatistik anzeigen

Die fit gibt ein Objekt zurück, das Informationen zu Änderungen der Verluste bei jeder nachfolgenden Iteration enthält. Mit diesem Objekt können wir einen geeigneten Verlustplan erstellen. Hoher Verlust bedeutet, dass die vom Modell vorhergesagten Fahrenheit-Grad weit von den wahren Werten im Array Fahrenheit_a entfernt sind.

Zur Visualisierung verwenden wir Matplotlib . Wie Sie sehen, verbessert sich unser Modell zu Beginn sehr schnell und verbessert sich dann stabil und langsam, bis die Ergebnisse am Ende des Trainings nahezu perfekt sind.

 import matplotlib.pyplot as plt plt.xlabel('Epoch') plt.ylabel('Loss') plt.plot(history.history['loss']) 

Wir verwenden das Modell für Vorhersagen.

Jetzt haben wir ein Modell, das auf die Eingabewerte celsius_q und die Ausgabewerte fahrenheit_a , um die Beziehung zwischen ihnen zu bestimmen. Wir können die Vorhersagemethode verwenden, um die Fahrenheit-Grad zu berechnen, um die wir zuvor die entsprechenden Grad Celsius nicht kannten.

Wie viel sind zum Beispiel 100,0 Grad Celsius Fahrenheit? Versuchen Sie zu erraten, bevor Sie den folgenden Code ausführen.

 print(model.predict([100.0])) 

Fazit:

[[211.29639]]


Die richtige Antwort lautet 100 × 1,8 + 32 = 212, also hat unser Modell ziemlich gut abgeschnitten!

Rückblick

• Wir haben ein Modell mit der Ebene " Dense .
• Wir haben sie mit 3.500 Beispielen trainiert (7 Wertepaare, 500 Trainingsiterationen).

Unser Modell hat die Werte der internen Variablen (Gewichte) in der Dense Ebene so angepasst, dass die korrekten Werte von Fahrenheit Grad auf einen beliebigen Eingabewert von Grad Celsius zurückgesetzt werden.

Wir schauen uns die Gewichte an

Lassen Sie uns die Werte der internen Variablen der Dense Ebene anzeigen.

 print("   : {}".format(l0.get_weights())) 

Fazit:

    : [array([[1.8261501]], dtype=float32), array([28.681389], dtype=float32)] 

Der Wert der ersten Variablen liegt nahe bei ~ 1,8 und der zweite bei ~ 32. Diese Werte (1,8 und 32) sind direkte Werte in der Formel zur Umrechnung von Grad Celsius in Grad Fahrenheit.

Dies kommt den tatsächlichen Werten in der Formel wirklich sehr nahe! Wir werden diesen Punkt in den folgenden Videos genauer betrachten, in denen wir zeigen, wie die Dense Ebene funktioniert. Im Dense müssen Sie jedoch nur wissen, dass ein Neuron mit einer einzelnen Eingabe und Ausgabe einfache Mathematik enthält - y = mx + b (als Gleichung) direkt), was nichts anderes ist als unsere Formel zur Umrechnung von Grad Celsius in Grad Fahrenheit, f = 1.8c + 32 .

Da die Darstellungen gleich sind, sollten die Werte der internen Variablen des Modells zu denen konvergieren, die in der tatsächlichen Formel dargestellt sind, was am Ende passiert ist.

Mit dem Vorhandensein zusätzlicher Neuronen, zusätzlicher Eingabewerte und Ausgabewerte wird die Formel etwas komplizierter, aber die Essenz bleibt dieselbe.

Ein bisschen experimentieren

Zum Spaß! Was passiert, wenn wir mehr Dense Schichten mit mehr Neuronen erstellen, die wiederum mehr interne Variablen enthalten?

 l0 = tf.keras.layers.Dense(units=4, input_shape=[1]) l1 = tf.keras.layers.Dense(units=4) l2 = tf.keras.layers.Dense(units=1) model = tf.keras.Sequential([l0, l1, l2]) model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) print("  ") print(model.predict([100.0])) print(" ,  100    {}  ".format(model.predict([100.0]))) print("    l0: {}".format(l0.get_weights())) print("    l1: {}".format(l1.get_weights())) print("    l2: {}".format(l2.get_weights())) 

Fazit:

    [[211.74748]]  ,  100    [[211.74748]]       l0: [array([[-0.5972079 , -0.05531882, -0.00833384, -0.10636603]], dtype=float32), array([-3.0981746, -1.8776944, 2.4708805, -2.9092448], dtype=float32)]     l1: [array([[ 0.09127654, 1.1659832 , -0.61909443, 0.3422218 ], [-0.7377194 , 0.20082018, -0.47870865, 0.30302727], [-0.1370897 , -0.0667181 , -0.39285263, -1.1399261 ], [-0.1576551 , 1.1161333 , -0.15552482, 0.39256814]], dtype=float32), array([-0.94946504, -2.9903848 , 2.9848468 , -2.9061244 ], dtype=float32)]     l2: [array([[-0.13567649], [-1.4634581 ], [ 0.68370366], [-1.2069695 ]], dtype=float32), array([2.9170544], dtype=float32)] 

Wie Sie vielleicht bemerkt haben, kann das aktuelle Modell auch die entsprechenden Grad Fahrenheit recht gut vorhersagen. Wenn wir jedoch die Werte der internen Variablen (Gewichte) von Neuronen nach Schichten betrachten, werden wir keine Werte ähnlich 1,8 und 32 sehen. Die zusätzliche Komplexität des Modells verbirgt die „einfache“ Form der Umrechnung von Grad Celsius in Grad Fahrenheit.

Bleiben Sie in Verbindung und im nächsten Teil werden wir uns ansehen, wie dichte Schichten „unter der Haube“ funktionieren.

Kurze Zusammenfassung

Glückwunsch! Sie haben gerade Ihr erstes Modell trainiert. In der Praxis haben wir gesehen, wie das Modell durch Eingabe- und Ausgabewerte gelernt hat, den Eingabewert mit 1,8 zu multiplizieren und 32 zu addieren, um das richtige Ergebnis zu erhalten.



Das war wirklich beeindruckend, wenn man bedenkt, wie viele Codezeilen wir schreiben mussten:

 l0 = tf.keras.layers.Dense(units=1, input_shape=[1]) model = tf.keras.Sequential([l0]) model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) model.predict([100.0]) 

Das obige Beispiel ist ein allgemeiner Plan für alle maschinellen Lernprogramme. Sie werden ähnliche Konstruktionen verwenden, um neuronale Netze zu erstellen und zu trainieren und nachfolgende Probleme zu lösen.

Trainingsprozess

Der Trainingsprozess (der in der Methode stattfindet model.fit(...)) besteht aus einer sehr einfachen Abfolge von Aktionen, deren Ergebnis die Werte interner Variablen sein sollten, um die Ergebnisse so nah wie möglich am Original zu erhalten. Der Optimierungsprozess, durch den solche Ergebnisse erzielt werden, der als Gradientenabstieg bezeichnet wird , verwendet eine numerische Analyse, um die am besten geeigneten Werte für die internen Variablen des Modells zu finden.

Um maschinelles Lernen zu betreiben, müssen Sie diese Details grundsätzlich nicht verstehen. Aber für diejenigen, die noch mehr lernen möchten: Der Gradientenabstieg durch Iterationen ändert die Parameterwerte ein wenig und „zieht“ sie in die richtige Richtung, bis die besten Ergebnisse erzielt werden. In diesem Fall bedeuten „beste Ergebnisse“ (beste Werte), dass jede nachfolgende Änderung des Parameters nur das Ergebnis des Modells verschlechtert. Eine Funktion, die misst, wie gut oder schlecht ein Modell bei jeder Iteration ist, wird als "Verlustfunktion" bezeichnet, und das Ziel jedes "Ziehens" (Anpassung interner Werte) besteht darin, den Wert der Verlustfunktion zu verringern.

Der Trainingsprozess beginnt mit dem Block „Direktverteilung“, in dem die Eingabeparameter zum Eingang des neuronalen Netzwerks gehen, den verborgenen Neuronen folgen und dann zum Wochenende gehen. Das Modell wendet dann interne Transformationen auf die Eingabewerte und internen Variablen an, um die Antwort vorherzusagen.

In unserem Beispiel ist der Eingabewert die Temperatur in Grad Celsius und das Modell hat den entsprechenden Wert in Grad Fahrenheit vorhergesagt.



Sobald der Wert vorhergesagt ist, wird die Differenz zwischen dem vorhergesagten und dem richtigen Wert berechnet. Der Unterschied wird als „Verlust“ bezeichnet und ist eine Form der Messung der Funktionsweise des Modells. Der Verlustwert wird durch die Verlustfunktion berechnet, die wir beim Aufruf der Methode durch eines der Argumente ermittelt haben model.compile(...).

Nach der Berechnung des Verlustwerts werden die internen Variablen (Gewichte und Verschiebungen) aller Schichten des neuronalen Netzwerks angepasst, um den Verlustwert zu minimieren und den Ausgabewert an den korrekten anfänglichen Referenzwert anzunähern.



Dieser Optimierungsprozess wird als Gradientenabstieg bezeichnet . Ein spezifischer Optimierungsalgorithmus wird verwendet, um einen neuen Wert für jede interne Variable zu berechnen, wenn die Methode aufgerufen wird model.compile(...). Im obigen Beispiel haben wir einen Optimierungsalgorithmus verwendet Adam.

Das Verständnis der Prinzipien des Trainingsprozesses ist für diesen Kurs nicht erforderlich. Wenn Sie jedoch neugierig genug sind, finden Sie weitere Informationen zum Google Crash-Kurs(Die Übersetzung und der praktische Teil des gesamten Kurses sind in den Veröffentlichungsplänen des Autors festgelegt.)

Zu diesem Zeitpunkt sollten Sie bereits mit den folgenden Begriffen vertraut sein:

• Eigenschaft : Eingabewert unseres Modells;
• Beispiele : Eingabe + Ausgabe-Paare;
• Tags : Modellausgabewerte;
• Schichten : eine Sammlung von Knoten, die innerhalb eines neuronalen Netzwerks miteinander verbunden sind;
• Modell : Darstellung Ihres neuronalen Netzwerks;
• Dicht und vollständig verbunden : Jeder Knoten in einer Schicht ist mit jedem Knoten aus der vorherigen Schicht verbunden.
• Gewichte und Offsets : Modellinterne Variablen;
• Verlust : die Differenz zwischen dem gewünschten Ausgabewert und dem tatsächlichen Ausgabewert des Modells;
• MSE : , , , .
• : , - ;
• : ;
• : «» ;
• : ;
• : ;
• : ;
• Rückausbreitung : Berechnung der Werte interner Variablen gemäß einem Optimierungsalgorithmus ausgehend von der Ausgabeschicht und in Richtung der Eingabeschicht durch alle Zwischenschichten.

Ebenen spüren

Im vorherigen Teil haben wir ein Modell erstellt, das Grad Celsius in Grad Fahrenheit umwandelt. Dabei wurde ein einfaches neuronales Netzwerk verwendet, um die Beziehung zwischen Grad Celsius und Grad Fahrenheit zu ermitteln.

Unser Netzwerk besteht aus einer einzigen vollständig verbundenen Schicht. Aber was ist eine vollständig verbundene Schicht? Um dies herauszufinden, erstellen wir ein komplexeres neuronales Netzwerk mit 3 Eingabeparametern, einer verborgenen Schicht mit zwei Neuronen und einer Ausgangsschicht mit einem einzelnen Neuron.



Denken Sie daran, dass ein neuronales Netzwerk als eine Reihe von Schichten vorgestellt werden kann, von denen jede aus Knoten besteht, die als Neuronen bezeichnet werden. Neuronen auf jeder Ebene können mit den Neuronen jeder nachfolgenden Schicht verbunden werden. Die Art der Schichten, in denen jedes Neuron einer Schicht mit dem anderen Neuron der nächsten Schicht verbunden ist, wird als vollständig verbundene (vollständig verbundene) oder dichte Schicht ( Dense-schicht) bezeichnet.



Wenn wir also vollständig verbundene Schichten verwenden keras, informieren wir Sie darüber, dass die Neuronen dieser Schicht mit allen Neuronen der vorherigen Schicht verbunden sein sollten.

Um das obige neuronale Netzwerk zu erstellen, reichen uns folgende Ausdrücke:

 hidden = tf.keras.layers.Dense(units=2, input_shape=[3]) output = tf.keras.layers.Dense(units=1) model = tf.keras.Sequential([hidden, output]) 

Also haben wir herausgefunden, was Neuronen sind und wie sie zusammenhängen. Aber wie funktionieren vollständig verbundene Schichten tatsächlich?

Um zu verstehen, was dort wirklich passiert und was sie tun, müssen wir „unter die Haube“ schauen und die interne Mathematik der Neuronen auseinander nehmen.



Stellen Sie sich vor, unser Modell empfängt drei Parameter - 1, 2, 3und 1, 2 3- die Neuronen unseres Netzwerks. Denken Sie daran, wir haben gesagt, dass ein Neuron interne Variablen hat? So, von w * und b * sind die internen Variablen Neuron, auch bekannt als das Gewicht und die Verdrängung. Es sind die Werte dieser Variablen, die im Lernprozess angepasst werden, um die genauesten Ergebnisse beim Vergleich der Eingabewerte mit der Ausgabe zu erhalten.



Was Sie auf jeden Fall beachten sollten, ist, dass die interne Mathematik des Neurons unverändert bleibt . Mit anderen Worten, während des Trainingsprozesses ändern sich nur Gewichte und Verschiebungen.

Wenn Sie anfangen, maschinelles Lernen zu lernen, mag es seltsam erscheinen - die Tatsache, dass es wirklich funktioniert, aber so funktioniert maschinelles Lernen!

Kehren wir zu unserem Beispiel für die Umrechnung von Grad Celsius in Grad Fahrenheit zurück.



Mit einem einzelnen Neuron haben wir nur ein Gewicht und eine Verschiebung. Weißt du was? Genau so sieht die Formel zur Umrechnung von Grad Celsius in Grad Fahrenheit aus. Wenn wir den w11Wert ersetzen 1.8und statt b1- erhalten 32wir das endgültige Transformationsmodell!

Wenn wir aus dem praktischen Teil auf die Ergebnisse unseres Modells zurückkommen, werden wir darauf achten, dass die Indikatoren für Gewicht und Verschiebung so „kalibriert“ wurden, dass sie ungefähr den Werten aus der Formel entsprechen.

Wir haben absichtlich ein solches praktisches Beispiel erstellt, um den genauen Vergleich zwischen Gewichten und Offsets klar darzustellen. Wenn wir maschinelles Lernen in die Praxis umsetzen, können wir die Werte von Variablen niemals auf diese Weise mit dem Zielalgorithmus vergleichen, wie im obigen Beispiel. Wie können wir das machen? Auf keinen Fall, da wir den Zielalgorithmus nicht einmal kennen!

Um die Probleme des maschinellen Lernens zu lösen, testen wir verschiedene Architekturen neuronaler Netze mit unterschiedlicher Anzahl von Neuronen. Durch Versuch und Irrtum finden wir die genauesten Architekturen und Modelle und hoffen, dass sie das Problem im Lernprozess lösen. Im nächsten praktischen Teil können wir spezifische Beispiele für diesen Ansatz untersuchen.

Bleiben Sie in Kontakt, denn jetzt beginnt der Spaß!

Zusammenfassung

In dieser Lektion lernten wir grundlegende Ansätze des maschinellen Lernens und lernten, wie vollständig verbundene Ebenen ( DenseEbenen) funktionieren. Sie haben Ihr erstes Modell darauf trainiert, Grad Celsius in Grad Fahrenheit umzurechnen. Sie haben auch die grundlegenden Begriffe des maschinellen Lernens gelernt, z. B. Eigenschaften, Beispiele und Beschriftungen. Sie haben unter anderem die wichtigsten Codezeilen in Python geschrieben, die das Rückgrat jedes Algorithmus für maschinelles Lernen bilden. Sie haben gesehen, dass Sie in wenigen Codezeilen mithilfe von TensorFlowund eine Vorhersage von einem neuronalen Netzwerk erstellen, trainieren und anfordern können Keras.

... und Standard-Handlungsaufforderung - anmelden, ein Plus setzen und teilen :)


YouTube: https://youtube.com/channel/ashmig
Telegramm: https://t.me/ashmig
VK: https://vk.com/ashmig