Es ist bekannt, dass die meisten Zeitreihen, mit denen sich ein Forscher befassen muss, nicht stationär sind und ihre Analyse wesentlich komplizierter ist als die Untersuchung stationärer Prozesse. Da das Interesse an Wavelets nachgelassen zu haben scheint, ist es nützlich, einige andere „instationäre“ Instrumente zu diskutieren, die hauptsächlich zur Schätzung von Momentanfrequenzen sowie zur Auswertung von Momentanspektren nützlich sind.
Zunächst ist es sinnvoll, sich an das „analytische Signal“ zu erinnern. Im Folgenden bezieht sich das "An-Modell" auf die momentane Impedanz und Leistung des Testsignals nach Fertigstellung seines Imaginärteils (phasenverschoben um π / 2).
Es ist jedoch nicht immer möglich, an der Gilbert-Transformation zu basteln. Zuvor wurde bereits ein autoregressives Spektralschätzungsverfahren erwähnt, das zum Arbeiten mit kurzen Sequenzen geeignet ist. Unter dem "AR-Modell" wird hier die Untersuchung kurzer (aus 5 Proben) überlappender Fragmente des ursprünglichen Signals verstanden, um die Autoregressionskoeffizienten zweiter Ordnung zu bestimmen, die "Pole" des Modells daraus zu finden usw.
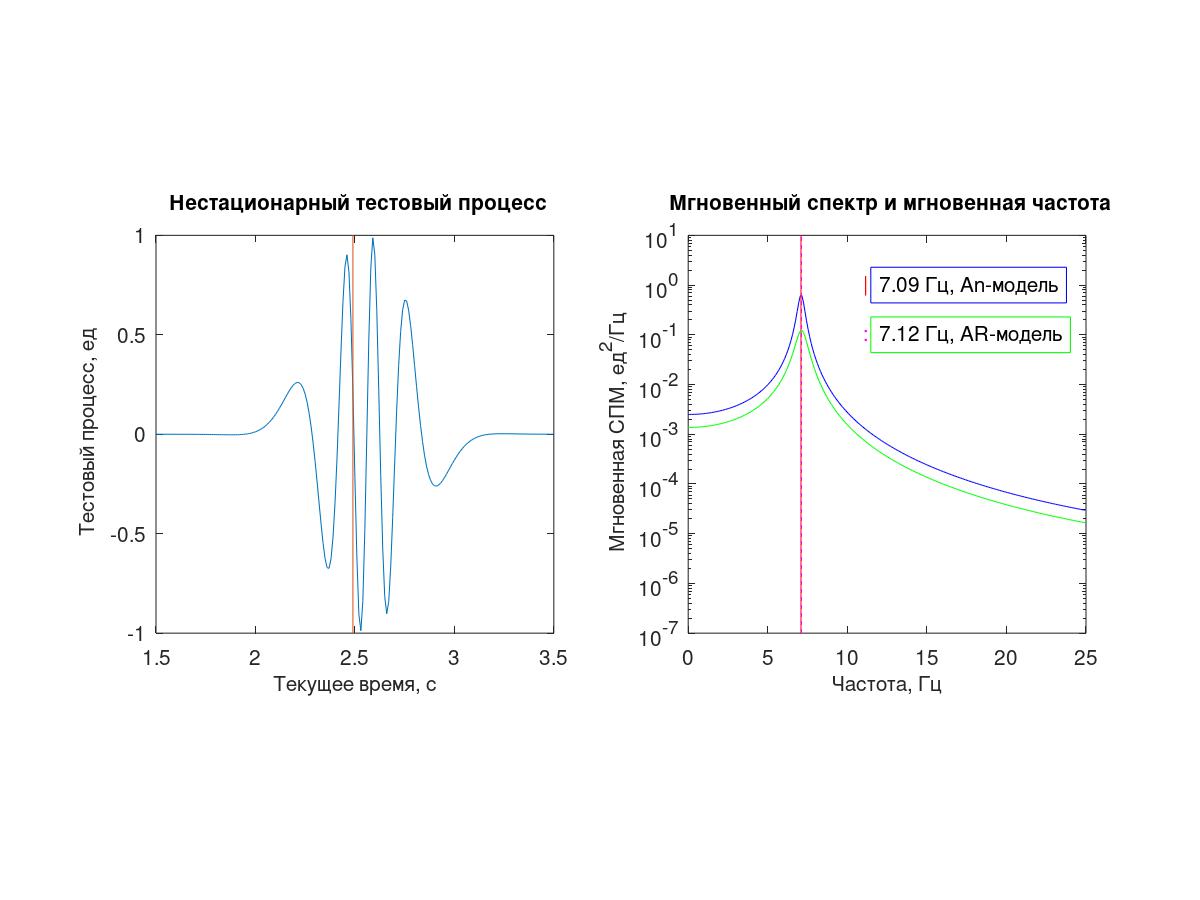

Beide hier beschriebenen Methoden basieren auf einem Prinzip - der Annahme, dass in einer kleinen Nachbarschaft des ausgewählten Zeitpunkts der untersuchte Prozess durch eine "exponentielle" Sequenz angenähert werden kann - ein Komplex (An) oder die Summe zweier komplexer konjugierter Exponentiale (AR).
Als Testprozess wurde eine Sequenz von 512 Proben mit einem bedingten Abtastintervall Δt = 0,01 s verwendet, die aus einem kontinuierlichen deterministischen Prozess (1) erhalten wurden.
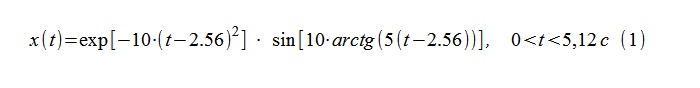
Durch "Logarithmus" und die anschließende Unterscheidung der Hochfrequenzfüllung bzw. der Hüllkurve von (1) werden theoretische Ausdrücke für (momentane) Frequenz und Dekrement (2) erhalten

Für die An-Modellierung nach der Periodogrammmethode (direkte und inverse Fourier-Transformation) wird aus der Anfangssequenz x [i] ein analytisches Signal y [i] erzeugt.
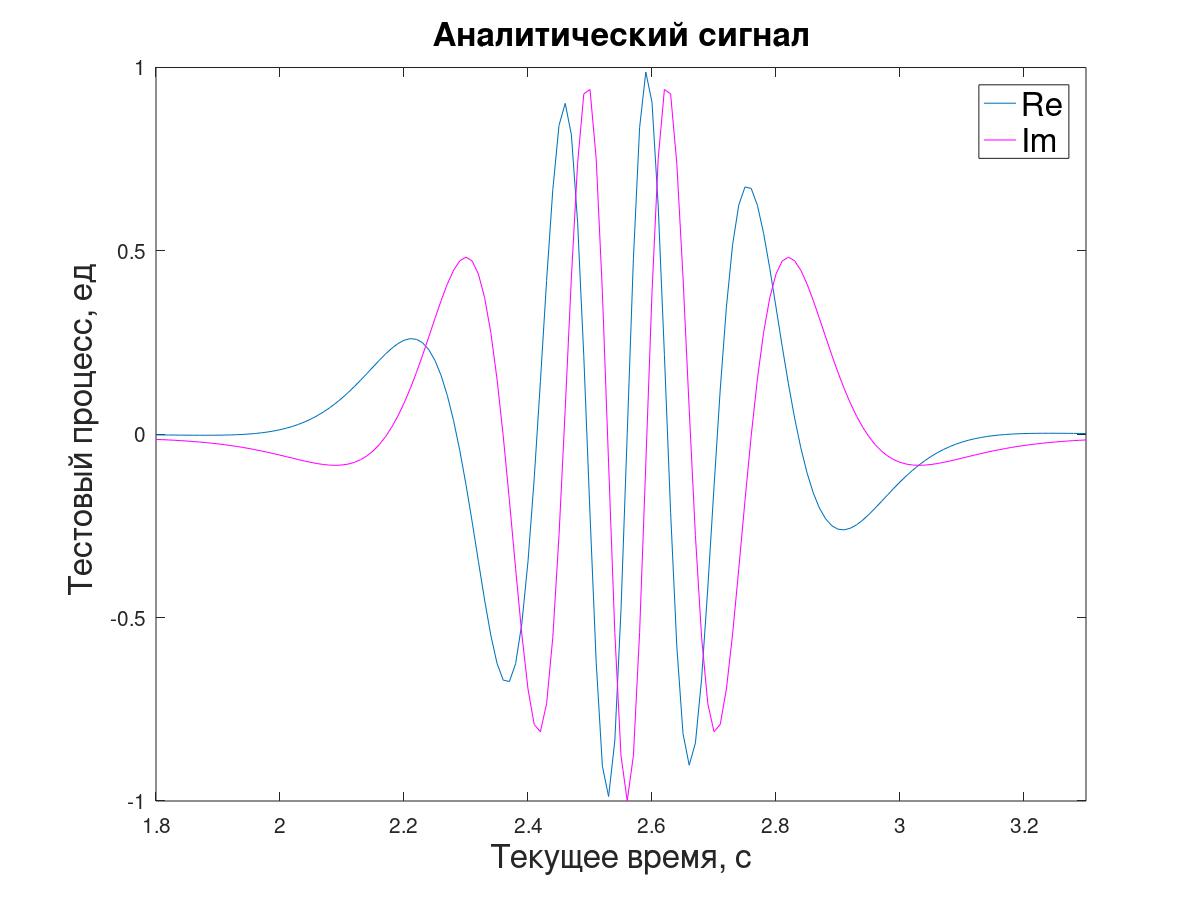
Das Verhältnis von zwei aufeinanderfolgenden Abtastwerten eines solchen Signals ermöglicht es im Prinzip, die momentane Impedanz λ zu bestimmen. Um diese Demonstrationsaufgabe zu vereinfachen - um nicht Zwischenabtastungen zu erstellen oder die Verschiebung der Schätzung um Δt / 2 zu erklären - wurde beschlossen, mit Abtastwerten „durch eins“ zu arbeiten und λ zu berechnen
i in Bezug auf die nachfolgenden y [i + 1] -Signalwerte zum vorherigen y [i-1] (3).

Für die AR-Modellierung (ein Modell zweiter Ordnung) wurde das Standardverfahren zur Berechnung der Autokorrelationskoeffizienten 1, a
1i , a
2i unter Verwendung der Yule-Walker-Gleichungen und die 5-Stichproben-Sequenzen x [i-2], x [i verwendet -1], ... x [i + 2] (4).
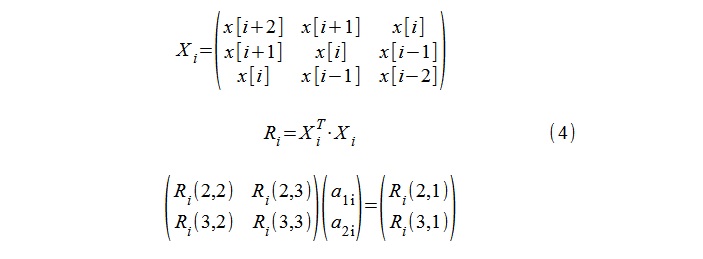
Die "Pole" des Modells λ
i lassen sich dann leicht durch Logarithmus der Wurzeln der quadratischen Gleichung (5) berechnen.
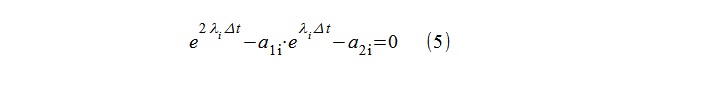

Die Konstruktion von Spektralschätzungen von den bekannten „Polen“ bis zu einem Skalierungsfaktor ist
nicht schwierig . Weiter. Die "Momentanleistung" für das An-Modell ist offensichtlich als | y [i] | definiert
2 , und die Frage der Skalierung dieser Schätzung scheint geklärt zu sein. Für das AR-Modell funktioniert die übliche Technik zur Bestimmung der Leistung von herkömmlichem weißem Rauschen im Fall eines instationären Signals nicht. In Ermangelung der besten Ideen wurde die Skalierung basierend auf dem durchschnittlichen Quadrat der entsprechenden 5 Stichproben angewendet. Es scheint, dass nichts mehr getan werden kann, wenn nur die Sequenz mit 5 Stichproben analysiert wird. Die Animation zeigt, wie das SPM-AR-Diagramm im Vergleich zum An-Score manchmal merklich „ausfällt“. Es versteht sich, dass die Momente des Übergangs „durch Null“ für das AR-Modell nicht nur in Bezug auf Fehler mit der Momentanfrequenz, sondern auch mit der Momentanamplitude, insbesondere im Niederfrequenzbereich, schwierig sein können.
Ein paar Kommentare am Ende.
- Erfahrungsgemäß liefern beide Methoden normalerweise gute Ergebnisse bei der Schätzung der Momentanfrequenz, zumindest im durchschnittlichen Frequenzbereich (basierend auf der Abtastfrequenz).
- Die relativ hohe Qualität der Ergebnisse der An-Methode, ihre Einfachheit und Leichtigkeit des Verständnisses und der Implementierung werden durch die möglichen Schwierigkeiten bei der Transformation des Prozesses nach Gilbert mehr als „kompensiert“. Ein Gilbert-Digitalfilter von guter Qualität, insbesondere in einem weiten Frequenzbereich, kann eine unannehmbar hohe Ordnung haben. Bei der Implementierung einer alternativen Periodogrammmethode dieser Transformation muss berücksichtigt werden, dass die Fourier-Transformation implizit den Abschluss des Prozesses auf periodisch impliziert. Infolgedessen kann ein signifikanter signifikanter Abschluss des Prozesses mit Nullen erforderlich sein. Die hohe Qualität der Ergebnisse der An-Methode erklärt sich aus der Verwendung von Informationen in einer sehr großen Nachbarschaft des ausgewählten Zeitpunkts (genau genommen - über die gesamte temporäre Implementierung des Prozesses), und dieselbe Eigenschaft macht es schwierig, die Methode zu implementieren (z. B. wenn in Echtzeit gearbeitet wird).
- Bei Bedarf können folgende Maßnahmen empfohlen werden, um die Ergebnisse der AR-Methode zu verbessern:
- Datenverdünnung (mit zu hoher Abtastrate)
- Eine Erhöhung der Anzahl der Mittelwerte - eine Erweiterung des „Zeitpunkts“ in der Modellnachbarschaft - die Konstruktion einer Spurmatrix X mit einer großen Anzahl von Zeilen.
- Erhöhen der Reihenfolge des AR-Modells.