Ein unerwarteter Blick auf geschwindigkeitsunabhängige asynchrone Schaltungen

In der asynchronen Wissenschaft nimmt der zentrale Platz die Eigenschaft von Schaltkreisen ein, die als Geschwindigkeitsunabhängigkeit bezeichnet werden, in englischer Sprache unabhängig (im Folgenden SI). Es wird angenommen, dass diese Eigenschaft ein Analogon der Unabhängigkeit von asynchronen Schaltungen von Verzögerungen von Logikelementen ist. Es überrascht nicht, dass der Begriff SI in fast allen Arbeiten zur Asynchronität erwähnt wird. In regelmäßigen Abständen treten jedoch einige vage Zweifel an diesem Begriff auf. Es ist kein Zufall, dass dieser Begriff zunehmend durch einen anderen Begriff ersetzt wird, der als Selbstsynchronisation bezeichnet wird. Ein Aufruf an die Quelle wird dazu beitragen, diese Situation zu klären. Wir sprechen über den zweiten Band des Buches von R. Millers Theorie der Schaltkreise, genauer gesagt Kapitel 10, genannt Theorie der Schaltkreise, unabhängig von der Geschwindigkeit.

Hier ist also die Definition von geschwindigkeitsunabhängigen Schaltungen.



Eine Klasse (Äquivalenz) ist ein vollständiger Satz zulässiger Zustände einer Schaltung, so dass für jeden Zustand aus diesem Satz eine Folge zulässiger Zustände existiert, die von einem gegebenen Zustand ausgehen und alle Zustände eines gegebenen Satzes enthalten. Mit anderen Worten, Sie können von jedem Status einer Klasse in jeden Status derselben Klasse gelangen.

Eine Klasse (Äquivalenz) ist endgültig, wenn es unmöglich ist, von den Zuständen einer bestimmten Klasse zu einem Zustand zu wechseln, der zu einer anderen Klasse gehört.

Zum Beispiel sind alle Lebensmuster (Verhaltensweisen) unabhängig von der Geschwindigkeit. Sie hängen auch nicht von der Geschwindigkeit der Schaltung ab, die schließlich notwendigerweise stoppt, und in einem einzigen Zustand.

Ferner stellt der Autor eine Verbindung zwischen SI-Schemata einerseits und semimodularen, sequentiellen Verteilungsschemata andererseits her. Abschließend zitiert er eine Liste bemerkenswerter Eigenschaften von Schaltkreisen, die unabhängig von der Geschwindigkeit sind.



Der erste Punkt ist besonders interessant. Es heißt nur, dass geschwindigkeitsunabhängige Schaltungen nicht von Verzögerungen von Logikelementen abhängen. Leider werden im Text die Gründe für diese Schlussfolgerung nicht ausdrücklich angegeben. Vielleicht ist dies der Grund für spätere Missverständnisse über den Begriff SI. In Wirklichkeit ist diese Schlussfolgerung völlig richtig. Zu Beginn von Kapitel 10 gibt der Autor Regeln für die Berechnung nachfolgender Zustände an.



Der Übergang der Schaltung in den nächsten Zustand ist das Ergebnis des Schaltens des Ausgangs eines Logikelements (oder der Ausgänge mehrerer Elemente). Das heißt, das Zeitintervall zwischen der Schaffung von Bedingungen zum Schalten eines Logikelements (Anregung) und dessen Schalten selbst ist durch nichts begrenzt. Und eine solche Zeitspanne ist eine Verzögerung des logischen Elements. Das heißt, der Autor geht von Anfang an von der Annahme aus, dass die Verzögerungen von Logikelementen beliebig groß sein können. In der Tat ist das Folgende etwas weiter geschrieben.



Nun, um alle Zweifel zu zerstreuen, ein Zitat aus der ersten Seite von Kapitel 10.



Somit wurde eine unbestreitbare Tatsache festgestellt: Die Unabhängigkeit von Verzögerungen von Logikelementen ist keine Eigenschaft einer Schaltung, sondern eine Eigenschaft des Modells, in dem diese Schaltung untersucht wird. Das heißt, jede Schaltung, SI oder nicht SI, die auf die gleiche Weise wie von R. Miller beschrieben untersucht wird, ist unabhängig von den Verzögerungen der Logikelemente. Gleichzeitig kann jede Schaltung mit begrenzter Verzögerung in einem Modell untersucht werden. In einem solchen Modell ist die Menge der zulässigen Zustände eine Teilmenge der Menge der zulässigen Zustände, wenn dasselbe Schema in einem Modell mit unbegrenzter Elementverzögerung betrachtet wird. Bei der Untersuchung einer Schaltung in einem Modell mit einer begrenzten Elementverzögerung kann die Schaltung geschwindigkeitsunabhängig sein und gleichzeitig von den Elementverzögerungen abhängen.

Somit stellt sich heraus, dass die Unabhängigkeit der Schaltung von den Verzögerungen von Logikelementen in keiner Weise mit der SI-Eigenschaft verbunden ist. Dann stellt sich die Frage: Was bringt es, eine Definition der Unabhängigkeit von der Geschwindigkeit einzuführen? Betrachten Sie in der Tat zwei Muster und ihr Verhalten.



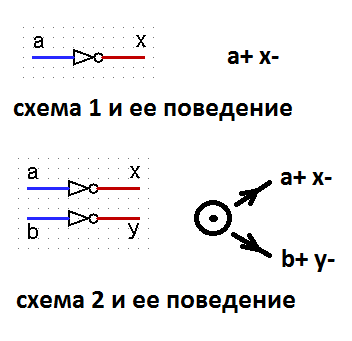
Die Signale a, b für beide Schaltungen werden eingegeben, die Signale x, y werden ausgegeben. Beide Schemata implementieren vollkommen vernünftige Verhaltensweisen. Gleichzeitig hängt die Schaltung 1 nicht von der Geschwindigkeit ab, und die Schaltung 2 hat keine solche Eigenschaft. Ja, wir können sagen, dass die Definition von SI eingeführt wurde, ohne die Signale in Eingabe und Ausgabe zu unterteilen. Aber eine solche Trennung der Signale durch den Autor wurde impliziert, und es gibt eine Bemerkung im Text darüber.

Die Aussagekraft und Angemessenheit der Einführung der Definition der SI-Eigenschaft wird nur im Zusammenhang mit der Semimodularitätseigenschaft offenbart. Bei Schaltungen mit der Eigenschaft der Halbmodularität kann jedes Signal seine Erregung nur durch sein Schalten entfernen. Nicht semi-modulare Schemata während der physischen Implementierung sind mit Störungen und metastabilen Zuständen behaftet. Nur semi-modulare Schemata können als stabil angesehen werden.

Der Zusammenhang zwischen den Eigenschaften der Semimodularität und der Unabhängigkeit von der Geschwindigkeit ist jedoch einseitig. Das heißt, semimodulare Schemata sind unabhängig von der Geschwindigkeit, aber das Gegenteil ist nicht der Fall. SI-Schaltungen sind möglicherweise nicht semi-modular. Das heißt, eine wirklich wichtige Eigenschaft, die Schaltungen nach Stabilität unterteilt, ist die Semimodularität. Es ist wichtig zu verstehen, dass semimodulare Schaltungen auch von Verzögerungen von Logikelementen abhängen können, wenn wir sie in einem Modell mit einer begrenzten Verzögerung betrachten.

Das ist aber noch nicht alles. Die Semimodularitätseigenschaft wird auch für autonome Schaltungen definiert, dh ohne die Signale in Eingang und Ausgang zu unterteilen. Aus diesem Grund erfüllen frei wählbare Schemata (Verhaltensweisen) nicht die Kriterien für die Semimodularität. In der Zwischenzeit können diese Schemata so stabil wie semi-modular sein. Zum Beispiel ist das obige Schema 2 nicht semi-modular, aber in Bezug auf die Stabilität ist es dem Schema 1, das semi-modular ist, in keiner Weise unterlegen.

Es gibt einen Ausweg aus dieser Sackgasse. Das Buch J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev „Logiksynthese für asynchrone Controller und Schnittstellen“ definiert die Definition der Eigenschaft der Ausgabepersistenz (OP).



Es ist die OP-Eigenschaft, die die eigentliche Eigenschaft ist, die Schemata (Verhalten) in stabil und nicht stabil trennt. Es ist die OP-Eigenschaft, die die SI-Eigenschaft ersetzen soll. Es sollte nicht vergessen werden, dass die Unabhängigkeit von Verzögerungen von Logikelementen eine Eigenschaft des Modells ist, in dem Schaltkreise (Verhaltensweisen) untersucht werden. Und OP-Schaltungen können auch von Elementverzögerungen abhängig sein, wenn sie in einem Modell mit begrenzter Verzögerung berücksichtigt werden.

Trotz aller bisherigen Kritik gibt es keine Beschwerden gegen R. Miller. Es gibt keine logischen Fehler in seiner Arbeit. Die Schuld für mehr als ein halbes Jahrhundert Fehler liegt eher bei Lesern, die die Arbeit von R. Miller falsch interpretiert haben.

Und schließlich eine angenehme Schlussfolgerung aus dem Vorstehenden. Das STG-Verhaltensmodell bietet eine unbegrenzte Verzögerung für Logikelemente. Die Regeln zum Ändern von Markierungen und zum Extrahieren der Wahrheitstabelle werden unter der Annahme unbegrenzter Verzögerungselemente formuliert. Daher ist jede Schaltung, die durch Berechnen logischer Funktionen unter Verwendung von STG (entweder unter Verwendung einer Wahrheitstabelle oder direkt unter Verwendung eines Graphen) erhalten wird, offensichtlich unabhängig von den Verzögerungen logischer Elemente. Es muss zwar verstanden werden, dass weitere Manipulationen mit dem resultierenden Schema zum Verlust dieser wertvollen Qualität führen können.