Es wurden Beweise dafür gefunden, dass alle Änderungen eine Mischung aus Ordnung und Zufall sind

Alle Beschreibungen der Veränderungen sind eine einzigartige Mischung aus Zufall und Determinismus, wie aus dem radikalen Beweis von Pinskers „schwacher Hypothese“ hervorgeht.

Stellen Sie sich einen Garten vor, in dem alle Blumen der Welt wachsen - zarte Orchideen, hoch aufragende Sonnenblumen, Wachsblumen des Carnegie-Kaktus und stinkende Blütenstände des titanischen Amorphophallus . Stellen Sie sich nun vor, dass all diese Pflanzenvielfalt auf nur zwei Optionen beschränkt ist und dass Sie durch Überkreuzen alle anderen produzieren können.

Dies ist die Natur eines der radikalsten Beweise, die in den letzten Jahren erhalten wurden. Es wurde von Tim Austin , einem Mathematiker von der University of California in Los Angeles, gemacht. Anstelle von Blumen ist Austins Arbeit jedoch mit einem der am besten untersuchten Objekte der Mathematik verbunden: einer mathematischen Beschreibung von Veränderungen.

Diese als dynamische Systeme bekannten Beschreibungen gelten für alles, von Planetenbewegungen bis hin zu Börsenschwankungen. Wo immer ein dynamisches System entsteht, wollen Mathematiker seine Grundlagen verstehen. Und eine der grundlegenden Tatsachen ist, dass jedes beliebig komplexe dynamische System in zufällige und deterministische Elemente unterteilt werden kann.

Diese Frage ist Gegenstand der „schwachen Hypothese“ von Pinsker, die erstmals in den 1970er Jahren formuliert wurde. Der Beweis der von Austin vorgelegten Hypothese bietet eine elegant intuitive Methode, um über alle möglichen obskuren Phänomene nachzudenken. Er zeigte, dass jedes dieser dynamischen Systeme im Wesentlichen eine Mischung aus Zufall und Determinismus ist.

Schicksal und Zufall

Ein dynamisches System beginnt mit einigen Eingabedaten, z. B. mit der Position des Pendels, wendet bestimmte Regeln an, z. B. Newtons Bewegungsgesetze, und erzeugt ein bestimmtes Ergebnis, z. B. die Position des Pendels in einer Sekunde. Was wichtig ist, dynamische Systeme ermöglichen es Ihnen, diesen Vorgang zu wiederholen: Sie können eine neue Position des Pendels einnehmen, dieselben Regeln anwenden und seine Position in einer weiteren Sekunde erhalten.

Dynamische Systeme sind auch rein mathematisch. Sie können die Startnummer auswählen, die Regel "Multiplizieren Sie die Nummer mit zwei" anwenden und eine neue erhalten. Mit diesem System können Sie auch die Gesamtzahl wieder in den Regelhandler eingeben und noch mehr Zahlen erhalten.

Bestimmte Arten dynamischer Systeme können als Kombination zweier einfacherer dynamischer Systeme ausgedrückt werden. Diese beiden Systeme arbeiten unabhängig voneinander, können jedoch zu einem komplexeren System kombiniert werden. Stellen Sie sich zum Beispiel ein dynamisches System vor, das einen Punkt entlang der Oberfläche eines Zylinders bewegt. Sie geben die Position des Punktes ein, wenden die Regeln an und erhalten einen weiteren Punkt.

Dieses System kann in zwei einfache zerlegt werden. Das erste ist ein dynamisches System, das einen Punkt um einen Kreis bewegt. Das zweite ist ein System, das einen Punkt vertikal auf und ab bewegt. Durch die Kombination von zwei Systemen - Kreisbewegung und Geradbewegung - erhalten wir eine komplexere Punktbewegung entlang des Zylinders.



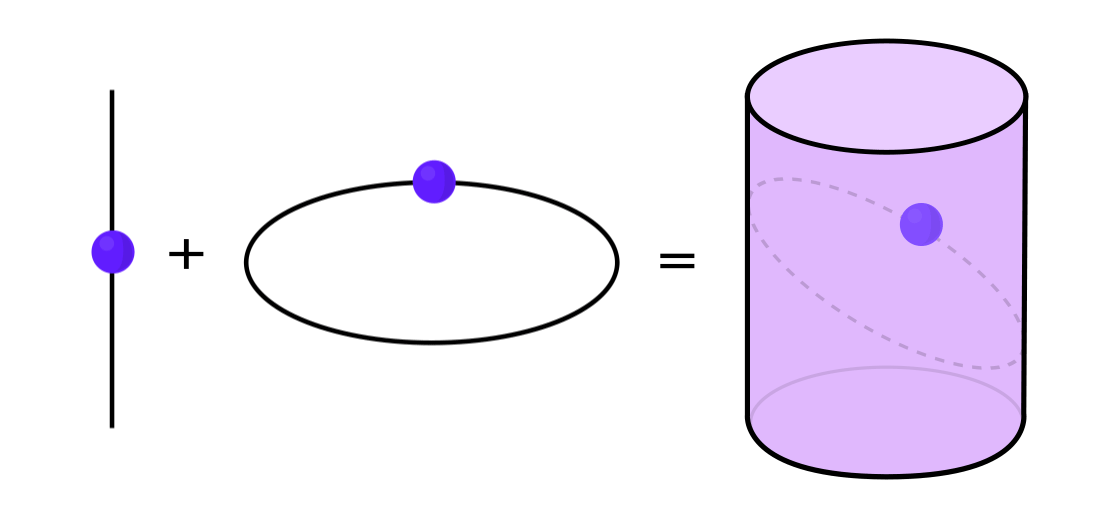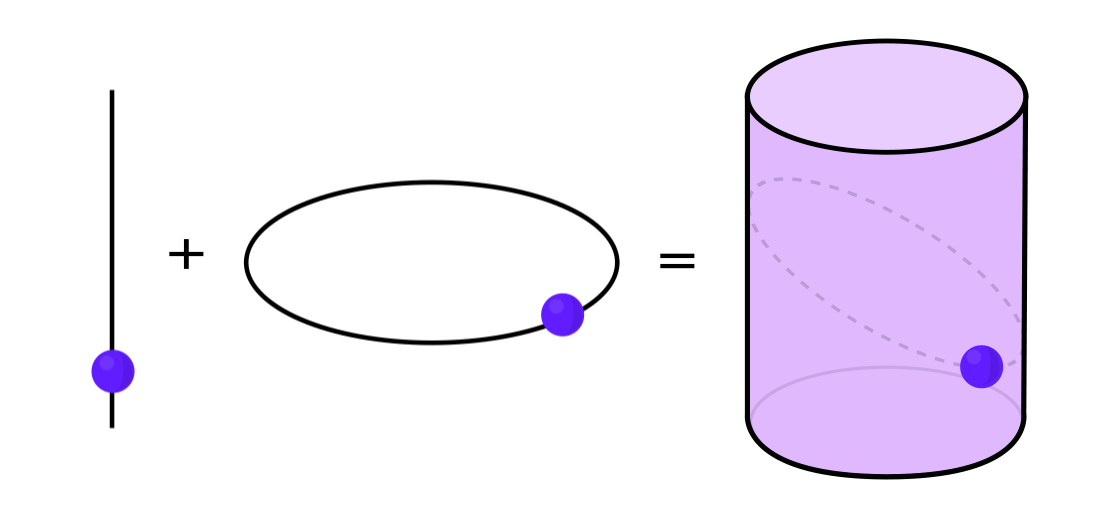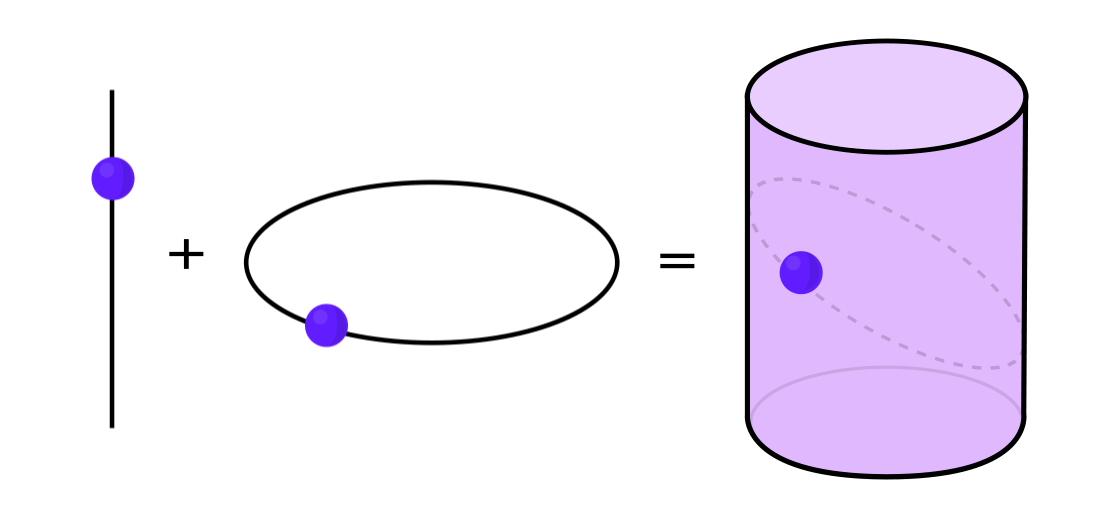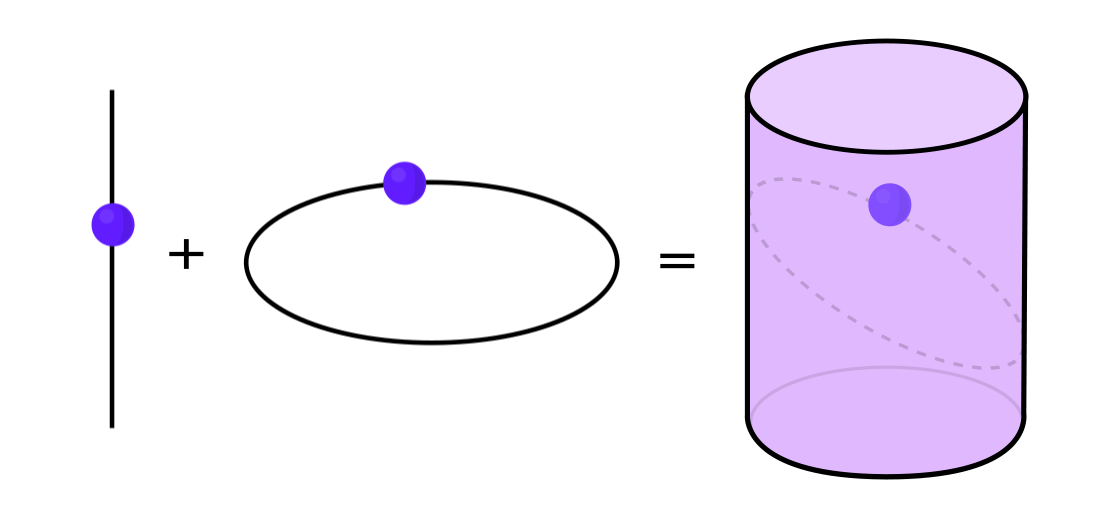
"Anstatt das gesamte dynamische System in seiner Gesamtheit zu studieren, muss man es in Teile zerlegen, kleine Teile, die für das Studium sinnvoll sind", sagte Catherine Lindsay , Mathematikerin am Boston College.

Es gibt zwei natürliche Kandidaten für die Rolle dieser Bausteine. Ersteres sind vollständig deterministische dynamische Systeme wie unser Pendelbeispiel. Wenn Sie die Position des Pendels zu einem bestimmten Zeitpunkt kennen, können Sie sie jederzeit in der Zukunft vorhersagen.


Jean-Paul Tuveno 1975, zwei Jahre vor der Formulierung von Pinskers schwacher Hypothese

Die zweite Art von dynamischen Systemen ist völlig zufällig. Stellen Sie sich zum Beispiel ein dynamisches System mit dieser Regel vor: Werfen Sie eine Münze. Wenn es einen Adler gibt, gehen Sie einen Schritt nach links. wenn Schwänze, richtig. Der endgültige Pfad ist völlig zufällig, dh selbst wenn Sie alles über den vorherigen Pfad wissen, helfen Ihnen diese Informationen nicht, den nächsten Schritt vorherzusagen.

Einige dynamische Systeme sind völlig zufällig, andere völlig deterministisch und die meisten liegen irgendwo dazwischen - sie sind eine Mischung aus beiden. Stellen Sie sich zum Beispiel eine leicht modifizierte Version unseres zufälligen Spaziergangs vor. Wir gehen einen Weg entlang, an dessen Rand Blumen gepflanzt werden und deren Farben ebenfalls zufällig sind. Die Regel bleibt dieselbe: Wenn ein Adler fällt, gehe nach links; wenn Schwänze, richtig. Wie wird die Reihenfolge der Blumenfarben sein?

Zuerst sagst du zufällig. Schließlich wurden die Farben selbst zufällig ausgewählt, und Ihre Bewegung ist auch zufällig. Nachdem Sie jedoch eine einzelne Blume passiert haben, steigt die Wahrscheinlichkeit, dass Sie sie in Zukunft passieren werden, einfach weil Sie nicht weit davon entfernt sind. Die Reihenfolge der Blütenfarben ist nicht völlig zufällig.

"Wenn Sie neben dem Rot stehen, erhöht sich die Wahrscheinlichkeit, dass Sie in zwei Schritten wieder auf das Rot treffen, da es vorkommen kann, dass Sie nach links und dann nach rechts treten und an denselben Ort zurückkehren", sagte Austin.

Solch ein „zufälliger Spaziergang durch eine zufällige Landschaft“ erzeugt eine Ausgabe - eine Folge von Farben - teils zufällig, teils nicht. 1960 schlug der Mathematiker Mark Pinsker vor, dass eine bestimmte große Klasse dynamischer Systeme die folgende Eigenschaft hat: Sie sind eine Mischung aus einem zufälligen dynamischen System mit einem deterministischen.

Pinskers Vermutung gilt für die Klasse der dynamischen Systeme, die eine wichtige gemeinsame Eigenschaft haben. Die Punkte in ihnen weichen nicht weit voneinander ab und schrumpfen während der Entwicklung des Systems nicht. Genauer gesagt, wenn Sie eine Schleife um eine Reihe von Punkten in Ihrem Raum zeichnen (der Raum kann so etwas wie eine Zylinderoberfläche sein), beginnen Sie über einen langen Zeitraum mit der Entwicklung eines dynamischen Systems und zeichnen Sie dann eine Schleife um die resultierende Menge von Punkten und dann um den Bereich, in dem die Punkte liegen Ende fällt mit dem Bereich zusammen, den sie am Anfang besetzt haben. Solche Systeme werden als "Maßnahmenerhaltung" bezeichnet.

"Wenn Pinskers ursprüngliche Hypothese wahr wäre, wäre es eine erstaunliche Beschreibung der Welt", sagte Assaf Naor , Mathematiker an der Princeton University. Aber Pinsker hat sich geirrt. 1973 widerlegte Donald Ornstein seine Hypothese. "Der Wortlaut war zu ehrgeizig", sagte Brina Kra , Mathematikerin an der Northwestern University.

In der Mathematik kommt es häufig vor, dass Mathematiker nach der Widerlegung der allgemeinen Hypothese versuchen, eine bescheidenere Version davon zu formulieren. 1977 schlug der Mathematiker Jean-Paul Tuveno die schwache Pinsker-Hypothese vor. Er machte die ursprüngliche Formulierung weicher und schlug vor, dass die dynamischen Systeme, die Pinsker im Sinn hatte, das Ergebnis der Kombination eines rein zufälligen Systems mit einem System waren, das fast vollständig deterministisch war.

Die Verfeinerung "fast" unterscheidet Tuvenos Hypothese von Pinskers Hypothese. Er meinte, dass ein einfaches deterministisches System eine Spur von Zufall haben sollte. Diese Spur verschwindet möglicherweise klein, sollte aber vorhanden sein. Und während er es ist, sagte Tuveno, wird Pinskers Idee funktionieren.

"Es war nahe an der ursprünglichen Hypothese, und Tuveno hat gezeigt, dass die Hypothese in diesem Fall eine Vielzahl hervorragender Anwendungen haben wird", sagte Naor.

In den folgenden Jahrzehnten gelang es den Mathematikern nicht, Pinskers schwache Hypothese zu beweisen. Der mangelnde Fortschritt ließ Tuveno denken, dass selbst seine geschwächte Formulierung sich als falsch herausstellen würde. "Irgendwann dachte ich, dass alles das Gegenteil sein würde, dass es nicht universell sein würde", sagte er.

Und dann erschien Tim Austin.

Schritt Lösung

Um Pinskers schwache Hypothese zu beweisen, musste ein genauer Weg gefunden werden, um ein dynamisches System zu sichten - eines, das es ihm ermöglichen würde, seine zufälligen und fast deterministischen Teile zu trennen. Frühere Arbeiten haben gezeigt, dass es am schwierigsten sein wird, Elemente mit ein wenig Zufälligkeit zu isolieren.

"Kleine Zufallsfaktoren sind viel schwieriger zu erfassen, und der zentrale Teil der Beweise besteht darin, einen Weg zu finden, um eine kleine Zufallsstruktur zu erkennen", sagte Tuveno.


Tim Austin, Mathematiker an der University of California in Los Angeles

Austin gelang es, mit kleinen zufälligen Elementen eines dynamischen Systems umzugehen, indem er die Perspektiven wechselte. Dynamische Systeme arbeiten in einem kontinuierlichen Raum, beispielsweise einem Punkt, der sich entlang der Oberfläche eines Zylinders bewegt, oder einem im Raum schwingenden Pendel. In diesen Räumen bewegen sich Punkte gemäß den Regeln eines dynamischen Systems entlang kontinuierlicher Bögen. Außerdem arbeiten diese Systeme in unendlich vielen Schritten - sie können für immer handeln.

Aber in seinem Beweis gab Austin den ununterbrochenen glatten Raum auf und vergaß die ewige Arbeit dynamischer Systeme. Stattdessen begann er zu analysieren, was passieren würde, wenn sie diskrete Zeiten wie eine Million Schritte arbeiten könnten. So wandte er die von Tuveno erfundene Methode an.

"Tuvenos Hauptbeitrag war, dass er erkannte, dass man die Eigenschaften eines dynamischen Systems beweisen kann, wenn man die richtigen mathematischen Schritte mit langen endlichen Linien ausführt", sagte Austin. "Mein Hauptbeitrag war, dass ich bewiesen habe, was für die langen Endlinien benötigt wird."

Austin stellte sich ein dynamisches System vor, das eine Folge von Einsen und Nullen ausgibt. Wenn das dynamische System eine Münze wirft, ist es leicht vorstellbar: Die Schwänze sind 1 und die Köpfe sind 0. Jedes dynamische System kann jedoch verwendet werden, um eine Binärsequenz zu erzeugen, indem einfach der Raum, in dem es arbeitet, in zwei geteilt wird (nicht unbedingt gleich). Teile.



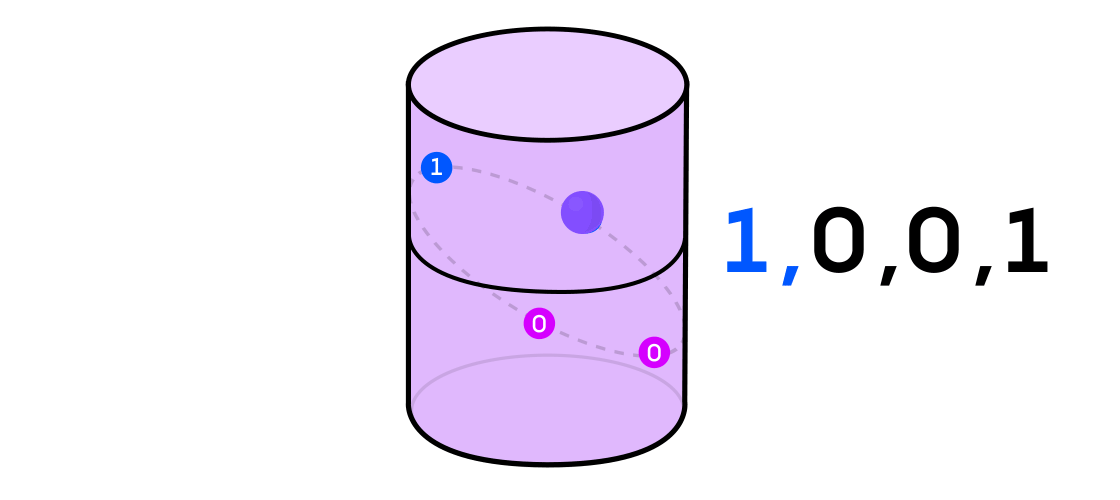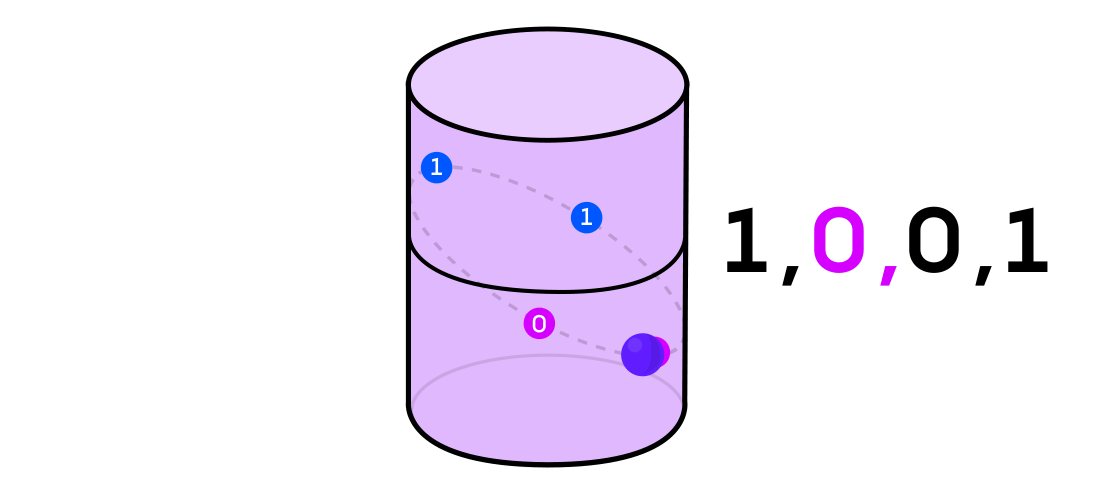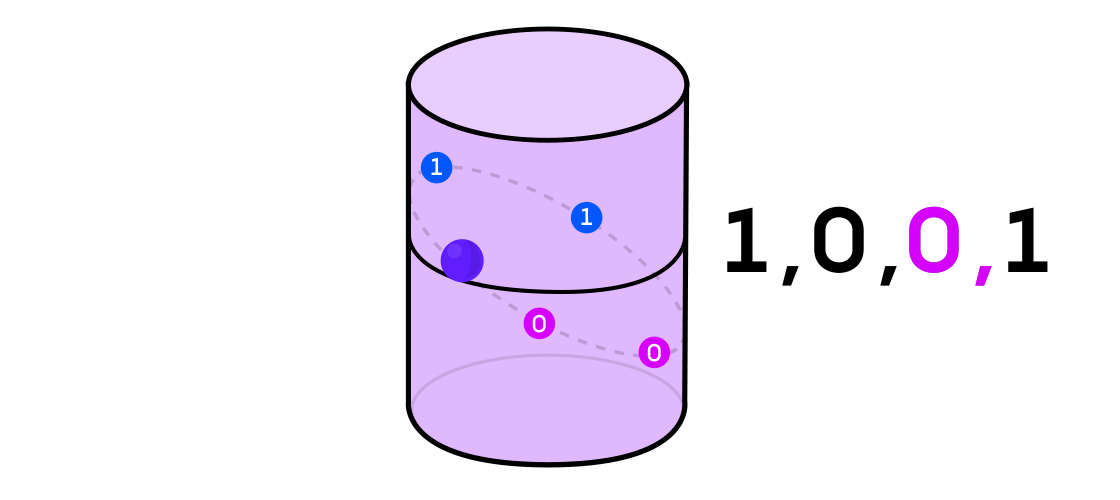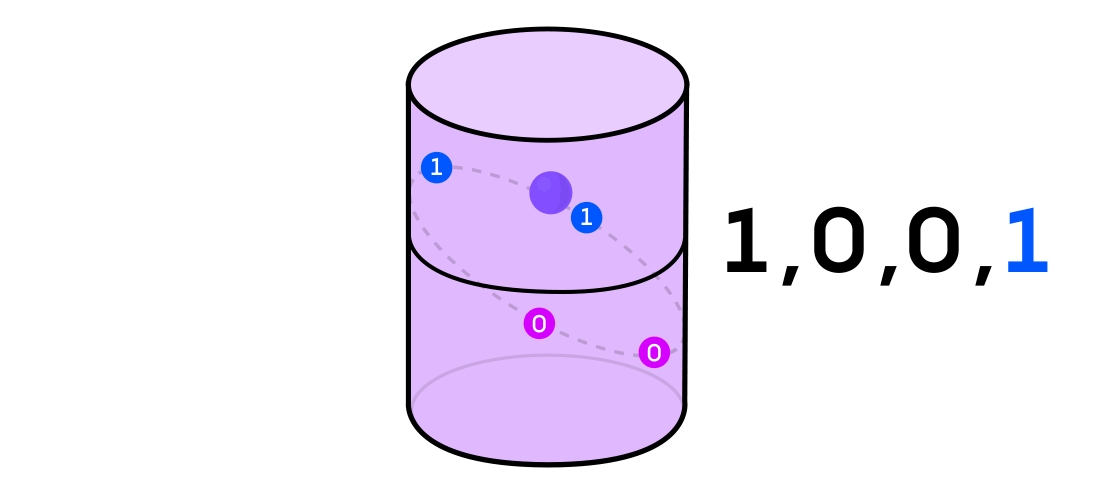
Zurück zum Beispiel eines dynamischen Systems auf einem Zylinder: Wenn sich der Punkt auf einem Teil des Zylinders befindet, bezeichnen Sie den Ausgabewert von System 1 und wenn auf dem anderen Teil 0.

Austin analysierte diese binären Sequenzen mit einem informationstheoretischen Tool namens Hamming Cubes . Stellen Sie sich einen Würfel von Eckpunkten vor, die durch Kanten verbunden sind. Jedem Scheitelpunkt werden Binärzahlen zugewiesen, z. B. 001 oder 101. Jedes Mal, wenn von einem Scheitelpunkt zu einem anderen gewechselt wird, ändert sich eine der drei Ziffern.

Hamming-Würfel können viel komplizierter sein als unsere, sie können genauso viel mehr Kanten und Scheitelpunkte in mehr Dimensionen als drei haben - aber sie haben alle die Eigenschaft, aufgrund derer der Abstand zwischen zwei beliebigen Scheitelpunkten - oder die Anzahl der Kanten, die Sie benötigen Von einem Scheitelpunkt zum anderen zu gehen, entspricht der Anzahl der Stellen, an denen die diesen Scheitelpunkten entsprechenden Informationslinien unterschieden werden. Daher befindet sich 000 im Abstand einer Kante von 001, zwei Kanten von 011 und drei von 111.



Um die zufälligen und deterministischen Elemente zu isolieren, aus denen ein komplexes dynamisches System besteht, dachte Austin darüber nach, wie oft ein dynamisches System eine bestimmte Folge von Nullen und Einsen erzeugen kann, die auf einem Hamming-Würfel dargestellt werden. Er bewies, dass diese Sequenzen auf bestimmte Weise in einem Würfel verteilt sind. Sie reichern sich in einer kleinen Anzahl von Würfel-Subregionen an - und dieser Cluster spiegelt den Determinismus des Systems wider -, sie sind jedoch zufällig auf die Sequenzen innerhalb dieser Cluster verteilt, was die Zufälligkeit des Systems widerspiegelt.

Ein solcher Kreisverkehr war notwendig, um ein Problem zu lösen, das direkten Angriffen nicht nachgab.

"Was mich überraschte, war nicht so sehr die Wahrheit oder Falschheit von Pinskers schwacher Hypothese, sondern wie sich herausstellte, weil diese Aufgabe so heimtückisch schien", sagte Lewis Bowen, Mathematiker an der Universität von Texas in Austin. "Bevor die Beweise erschienen, hatten wir im Großen und Ganzen keine Ahnung, ob dies überhaupt möglich ist."

Das Ergebnis von Austin verleiht einer Vielzahl dynamischer Systeme die Grundstruktur. Für Mathematiker, die sich häufig zwischen Objekten drehen, die miteinander verbunden zu sein scheinen, ist nicht klar, wie der Beweis ihre genaue Geographie angibt. Jetzt haben sie einen Leitfaden für diese dynamischen Systeme, obwohl noch nicht bekannt ist, zu welchen Entdeckungen dies führen wird.

"Mathematiker sind immer an den Bausteinen interessiert, aus denen alles besteht", sagte Lindsay. "Austins Beweis ist ein hervorragendes Ergebnis, das wahrscheinlich viele Anwendungen in der reinen Mathematik haben wird, aber ich kann nicht sagen, was sie sein werden."