🔲 💻 👵 Wavelet-Analyse. Teil 3 🌪️ ✊🏽 🗓️

Einführung

Bei der Durchführung einer CWT-Analyse mit der PyWavelets-Bibliothek (einer kostenlosen Open Source-Software, die unter der MIT-Lizenz veröffentlicht wurde) treten Probleme bei der Visualisierung des Ergebnisses auf. Das von den Entwicklern vorgeschlagene Visualisierungstestprogramm ist in der folgenden Liste aufgeführt:

Auflistung

import pywt import numpy as np import matplotlib.pyplot as plt t = np.linspace(-1, 1, 200, endpoint=False) sig = np.cos(2 * np.pi * 7 * t) + np.real(np.exp(-7*(t-0.4)**2)*np.exp(1j*2*np.pi*2*(t-0.4))) widths = np.arange(1, 31) cwtmatr, freqs = pywt.cwt(sig, widths, 'cmor1-1.5') plt.imshow(cwtmatr, extent=[-1, 1, 1, 31], cmap='PRGn', aspect='auto', vmax=abs(cwtmatr).max(), vmin=-abs(cwtmatr).max()) # doctest: +SKIP plt.show() # doctest: +SKIP

Bei der Arbeit mit komplexen Wavelets, beispielsweise mit 'cmor1-1.5', erzeugt das Programm einen Fehler:

 File"C:\Users\User\AppData\Local\Programs\Python\Python36\lib\site-packages\matplotlib\image.py", line 642, in set_data raise TypeError("Image data cannot be converted to float") TypeError: Image data cannot be converted to float

Dieser Fehler sowie Schwierigkeiten bei der Auswahl der Skala (Breiten) zur Bereitstellung der erforderlichen Zeitauflösung machen es insbesondere für Anfänger schwierig, die CWT-Analyse zu studieren, was mich dazu veranlasste, diesen Artikel pädagogischer Natur zu schreiben.

Der Zweck dieser Veröffentlichung ist es, die Verwendung des neuen Skalierungsvisualisierungsmoduls für die Analyse einfacher und spezieller Signale sowie bei Verwendung von Normalisierungsmethoden, logarithmischer Skalierung und Synthese zu berücksichtigen, die zusätzliche Informationen bei der Analyse von Zeitreihen liefern.

Der Artikel verwendete Informationen aus der Veröffentlichung „Eine sanfte Einführung in Wavelet für die Datenanalyse“ . In den Auflistungen der in der Veröffentlichung angegebenen Beispiele werden die Fehler behoben, und jede Auflistung des Beispiels wird in seine fertige Form gebracht, sodass es verwendet werden kann, ohne mit den vorherigen vertraut zu sein. Für die Wavelet-Analyse spezieller Signale wurden Daten aus der PyWavelets-Probendatenbank verwendet.

Ein Wavelet-Skalogramm ist eine zweidimensionale Darstellung eindimensionaler Daten. Die Zeit ist auf der X-Achse aufgetragen, und auf der Y-Achse ist eine Skala dargestellt - das Ergebnis der Wavelet-Transformation des Signals entsprechend der Signalamplitude zum Zeitpunkt X. Der analytische Wert einer solchen grafischen Anzeige des Signals besteht darin, dass die Zeitauflösung auf der Y-Achse angezeigt wird, die zusätzliche Informationen liefert über die dynamischen Eigenschaften des Signals.

Wavelet - Einfache Signalskalogramme

1. Kosinuswelle mit einer Gaußschen Hüllkurve (Ersetzen von Wavelets. Sie können die Abhängigkeit der Zeitauflösung von der Skala untersuchen):

Auflistung

 from numpy import* from pylab import* import scaleogram as scg import pywt #  ,        #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) p1=10; periodic1 = cos(2*pi/p1*time) * exp(-((time-ns/2)/200)**2) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(periodic1); ax1.set_xlim(0, len(time)) ax1.set_title("   ") fig1.tight_layout() ax2 = scg.cws(periodic1, scales=scales, figsize=(6.9,2.9)); txt = ax2.annotate("p1=%s"%p1, xy=(100, 10), bbox=dict(boxstyle="round4", fc="w")) tight_layout() print("    :", scg.get_default_wavelet(), "(", pywt.ContinuousWavelet(scg.get_default_wavelet()).family_name, ")") show()

Wavelet-Funktion zur Signalumwandlung: cmor1-1.5 (Complex Morlet Wavelets)

Das periodische Signal erscheint nun in Form eines horizontalen kontinuierlichen Streifens am Punkt Y = p1, dessen Intensität in Abhängigkeit von der Amplitude des periodischen Signals variiert.

Die Erkennung weist eine gewisse Unschärfe auf, da die Bandbreite nicht gleich Null ist. Dies liegt an der Tatsache, dass die Wavelets nicht eine Frequenz, sondern ein Band erfassen. Dieser Effekt ist mit der Wavelet-Bandbreite verbunden.

2. Drei Impulse werden mit zunehmender Periode nacheinander addiert (Um periodische Variationen in verschiedenen Maßstäben zu berücksichtigen: Analyse mit mehreren Auflösungen):

Auflistung

 from numpy import* import pandas as pd from pylab import* import scaleogram as scg #          #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) pulses = zeros(ns, dtype=float32) steps = linspace(0, ns, 8) periods = [10, 20, 40] for i in range(0,3): step_mask = (time > steps[i*2+1]) & (time < steps[i*2+2]) pulses += cos(2*pi/periods[i]*time) * step_mask fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(pulses); ax1.set_xlim(0, len(time)); ax1.set_title("     "); ax1.set_xlabel("Time") fig1.tight_layout() ax2 = scg.cws(pulses, scales=scales, figsize=(7,3)) for i in range(0, 3): txt = ax2.annotate("p%d=%ds"%(i+1,periods[i]), xy=(steps[i*2]+20, periods[i]), bbox=dict(boxstyle="round4", fc="w")) ax2.plot(steps[i*2+1]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) ax2.plot(steps[i*2+2]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) tight_layout() show()

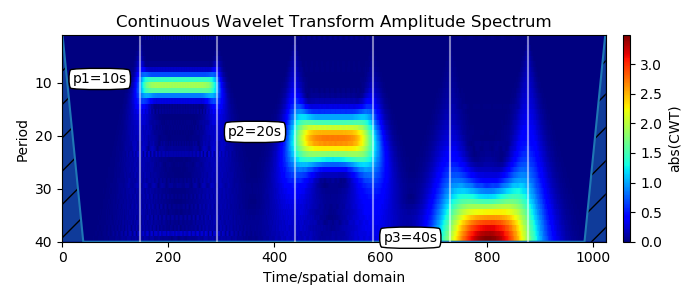
Impulse erscheinen an der erwarteten Stelle Y, entsprechend ihrer Periodizität, sie sind in Frequenz und Zeit lokalisiert. Der Anfang des Streifens und das Ende entsprechen dem Impuls.
Die Bandbreite skaliert mit der Länge des Zeitraums. Dies ist eine bekannte Eigenschaft der Wavelet-Transformation: Wenn die Skala zunimmt, nimmt die zeitliche Auflösung ab. Dies wird auch als Kompromiss zwischen Zeit und Frequenz bezeichnet. Wenn Sie sich ein Spektrogramm dieses Typs ansehen, führen Sie viele Auflösungsanalysen durch.

3. Drei periodische Schwingungen mit unterschiedlichen Frequenzen gleichzeitig (die Wavelet-Analyse kann die Komponenten des Signals nach Frequenz unterscheiden, wenn ihre Unterschiede signifikant sind):

Auflistung

 from numpy import* import pandas as pd from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) allwaves = np.zeros(ns, dtype=np.float32) periods = [10, 20, 40] for i in range(0,3): allwaves += cos(2*np.pi/periods[i]*time) fig1, ax1 = subplots(1, 1, figsize=(6.5,2)); lines = ax1.plot(allwaves); ax1.set_title("  ") ax1.set_xlim(0, len(time)); ax1.set_xlabel("") fig1.tight_layout() ax2 = scg.cws(allwaves, scales=scales, figsize=(7,2)) tight_layout() show()

4. Ein nicht sinusförmiges periodisches Signal (Die Differenz der Wavelet-Transformationen eines Dreieckswellensignals mit einer Periode von 30 Sekunden gegenüber den zuvor betrachteten wird berücksichtigt):

Auflistung

 from numpy import* from pylab import* import scipy.signal import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) ptri = 30.0 # period in samples raising = 0.8 # fraction of the period raising triangle = scipy.signal.sawtooth(time/ptri*2*pi, raising) # plot the signal fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(triangle); ax1.set_xlim(0, len(time)) ax1.set_title("triangle wave increasing 80% of the time with a 30s period") fig1.tight_layout() # and the scaleogram ax2 = scg.cws(triangle, scales=scales, figsize=(7,3)); txt = ax2.annotate("first harmonic", xy=(100, 30), bbox=dict(boxstyle="round4", fc="w")) txt = ax2.annotate("second harmonic", xy=(100, 15), bbox=dict(boxstyle="round4", fc="w")) tight_layout() show()

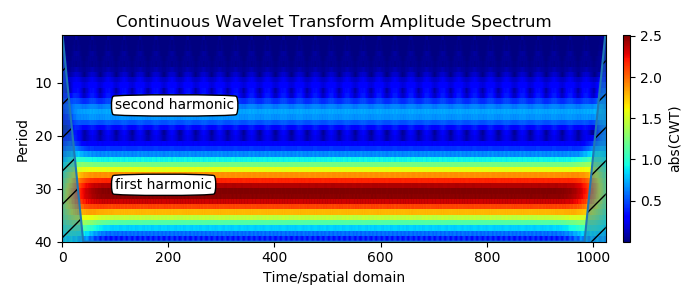
Eine große Band ist die erste Harmonische. Die zweite Harmonische ist genau zum halben Wert der Periode der ersten Harmonischen sichtbar. Dies ist das erwartete Ergebnis für periodische nicht sinusförmige Signale. Um die zweite Harmonische herum erscheinen unscharfe vertikale Elemente, die schwächer sind und für eine dreieckige Wellenform eine Amplitude von 1/4 der ersten haben.

5. Glatte Impulse (Gaußsche Impulse) ähneln realen Datenstrukturen. (Dieses Beispiel zeigt, wie mithilfe der Wavelet-Analyse lokalisierte Signaländerungen im Zeitverlauf erkannt werden.)

Eine Reihe von glatten Impulsen mit unterschiedlichen Sigma-Werten:

$2 \ cdot \ sigma _ {1} = 2$
$2 \ cdot \ sigma _ {2} = 10$
$2 \ cdot \ sigma _ {3} = $ 2$

Pulsbreite:

$\ omega _ {1} = 2$
$\ omega _ {2} = $ 2$
$\ omega _ {3} = $ 10$

Auflistung

 from numpy import* from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) #       s1=1; s2=5; s3=10 events = [ns*0.1, ns*0.3, ns*0.7] bumps = exp(-((time-events[0])/s1)**2) + exp(-((time-events[1])/s2)**2) + \ exp(-((time-events[2])/s3)**2) #      w1=1; w2=5; w3= 50 steps = ((time > events[0]-w1) & (time < events[0]+w1)) + \ ((time > events[1]-w2) & (time < events[1]+w2)) + \ ((time > events[2]-w3) & (time < events[2]+w3)) #   fig1, (ax1, ax2) = subplots(1, 2, figsize=(11, 2)); ax1.set_title("Bumps"); ax2.set_title("Steps") lines = ax1.plot(bumps); ax1.set_xlim(0, len(time)) lines = ax2.plot(steps); ax2.set_xlim(0, len(time)) fig1.tight_layout() #   scales_bumps = scg.periods2scales(arange(1, 120, 2) ) fig2, (ax3, ax4) = subplots(1, 2, figsize=(14,3)); ax3 = scg.cws(bumps, scales=scales_bumps, ax=ax3) ax4 = scg.cws(steps, scales=scales_bumps, ax=ax4) for bmpw, stepw in [(2*s1, 2*w1), (2*s2,2*w2), (2*s3, 2*w3)]: ax3.plot(ax3.get_xlim(), bmpw*ones(2), 'w-', alpha=0.5) ax4.plot(ax4.get_xlim(), stepw*ones(2), 'w-', alpha=0.5) fig2.tight_layout() show()

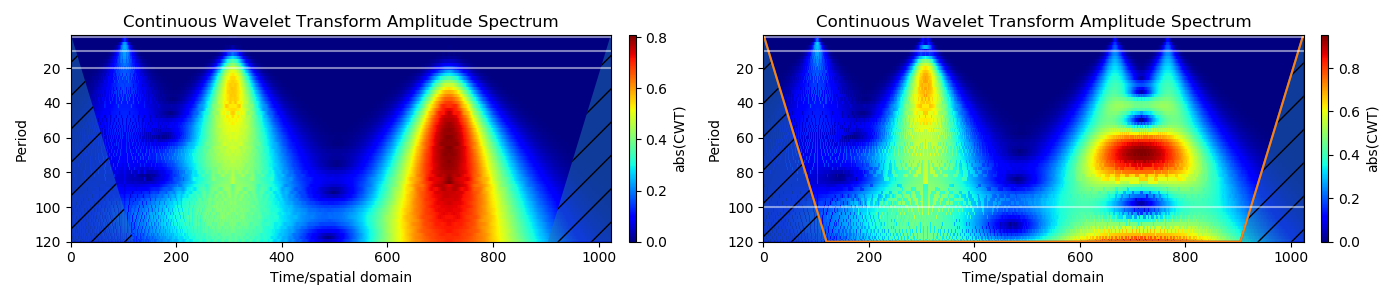
Diskrete Impulse erzeugen im Sialogramm konische Strukturen, die auch als Einflusskegel bezeichnet werden. Glatte Impulse (Gaußsche Impulse) ähneln realen Datenstrukturen und erzeugen Kegel, die sich zu großen Maßstäben ausdehnen. Die horizontalen Führungslinien entsprechen ungefähr Zeiträumen (2 s, 10 s, 20 s). Daher ähnelt der Impuls einem periodischen Signal mit einer Periode.

6. Rauschen (Rauschen im Sialogramm anzeigen):

Auflistung

 from numpy import* from pylab import* import scaleogram as scg import random scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) noise =random.sample(range(ns), ns) fig1, ax1 = plt.subplots(1, 1, figsize=(6.2,2)); ax1.set_title("  ") lines = ax1.plot(time, noise) ax1.set_xlim(0, ns) fig1.tight_layout() ax2 = scg.cws(noise, scales=scales, figsize=(7,2)) tight_layout() show()

Rauschen wird normalerweise als eine Reihe von Elementen angezeigt, und einige Unregelmäßigkeiten können wie Objekte realer Daten aussehen. Wenn Sie also reale Daten verwenden, müssen Sie vorsichtig sein und gegebenenfalls den Rauschpegel überprüfen. Der obere Zeitplan ist bei jedem Programmstart anders.

Wavelet-Skalogramme von Spezialsignalen

Die PyWavelets-Datenbank enthält zwanzig spezielle Wavelet-Transformationssignale, die sowohl für Studien als auch für die Entwicklung nützlich sind. Daher werde ich eine Liste geben, mit der Sie eine Wavelet-Analyse aller zwanzig Signale durchführen können:

Auflistung

 #!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from pylab import* import scaleogram as scg import pywt signals = pywt.data.demo_signal('list') signal_length=1024 for signal in signals: if signal in ['Gabor', 'sineoneoverx']: x = pywt.data.demo_signal(signal) else: x = pywt.data.demo_signal(signal, signal_length) times=[] signals=[] for time, sig in enumerate(x.real): times.append(time) signals.append(sig) scg.set_default_wavelet('cmor1-1.5') scales = scg.periods2scales( arange(1, 40) ) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(signals); ax1.set_xlim(0, len(times)) ax1.set_title("%s"%signal) fig1.tight_layout() ax2 = scg.cws(signals, scales=scales, figsize=(6.9,2.9)); tight_layout() show()

Ich werde nur ein Ergebnis der Wavelet-Transformation des Dopplersignals geben:

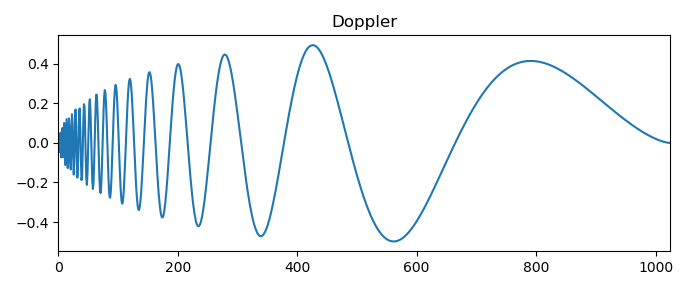
Es werden die häufigsten Arten von einfachen und speziellen Signalen betrachtet, die es uns ermöglichen, auf die Verwendung eines Skalogramms umzuschalten, um einige Probleme der Zeitreihenanalyse zu lösen.

Wavelet-Timeline-Skalogramme

1. CDC-Fertilitätsdaten in den USA 1969-2008 (Fertilitätsdaten enthalten periodische Merkmale, sowohl auf jährlicher als auch auf kleinerer Ebene):

Auflistung

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) fig = figure(figsize=(12,2)) lines = plot(births.index, births.values/1000, '-') xlim(datetime_lim) ylabel("Nb of birthes [k]"); title("Total births per day in the US (CDC)"); xlim = xlim() ax = scg.cws(births, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()

Eine horizontale Linie erscheint mit einer Häufigkeit von ungefähr 7 Tagen. Hohe Werte erscheinen in der Nähe der Grenzen der Skala, was das normale Verhalten der Wavelet-Verarbeitung ist. Diese Effekte sind als Einflusskegel bekannt, weshalb eine (optionale) Maske diesen Bereich überlagert.

2. Normalisierung (Entfernen des Durchschnittswerts - geburts_normed = Geburten-Geburten.Mittel () ist obligatorisch, andernfalls werden die Datengrenzen als Stufen betrachtet, die viele falsche kegelförmige Erkennungen erzeugen):

Auflistung

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() ax = scg.cws(births_normed, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()

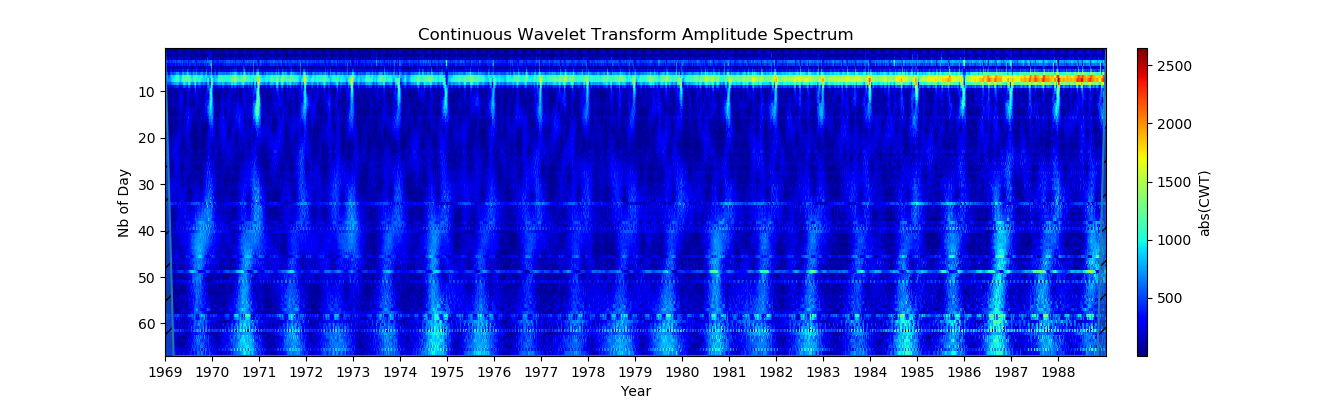
3. Änderung der Amplitudenskala (Um Jahresobjekte mit period2scales () anzuzeigen, wird die Skalierung entlang der Y-Achse angegeben).

Auflistung

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 5), xlabel="Year", ylabel="Nb of Day", clim=(0, 2500)) set_x_yearly(ax, len(births)) show()

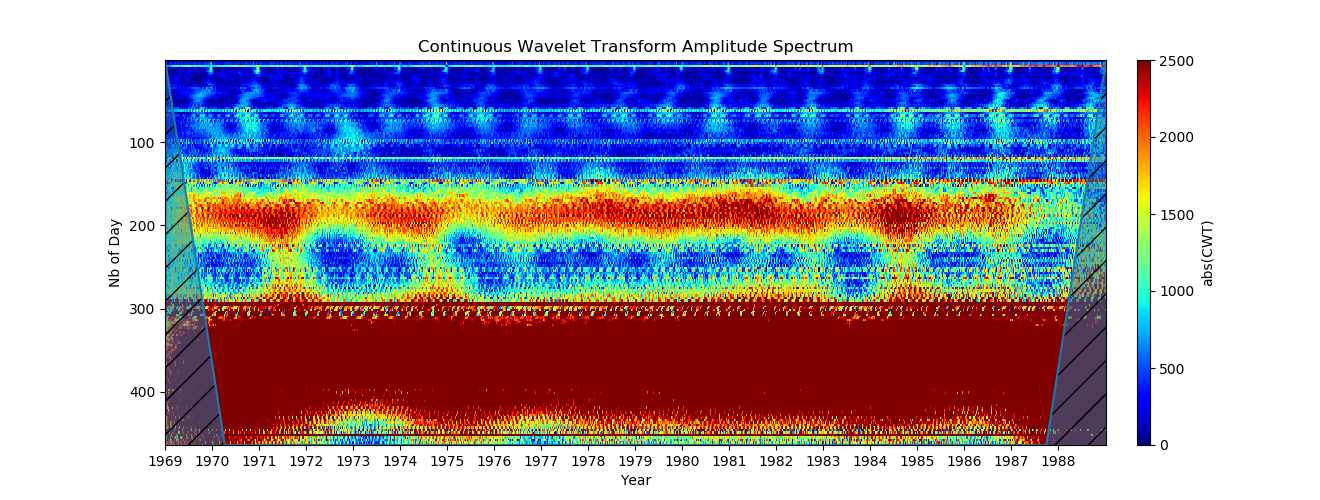
Der Amplitudenbereich der Farbkarte (Y-Achse) wird nun durch klim = (0,2500) eingestellt. Der genaue Wert für die Amplitude der Schwingungen hängt vom Wavelet ab, bleibt jedoch nahe der Größenordnung des tatsächlichen Werts. Das ist viel besser, jetzt sehen wir sehr gut die jährliche Variation sowie ungefähr 6 Monate!

4. Verwenden der logarithmischen Skala (Um kleine und große Perioden gleichzeitig anzuzeigen, ist es besser, die logarithmische Skala auf der Y-Achse zu verwenden. Dies wird mit der Option xscale = log erreicht.)

Auflistung

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) print("Number of available days:", len(births_normed)) show()

Das Ergebnis ist viel besser, aber jetzt werden Pixel mit niedrigen Periodenwerten entlang der Y-Achse verlängert.

5. Gleichmäßige Verteilung auf einer logarithmischen Skala (Um eine gleichmäßige Verteilung auf einer Skala zu erhalten, müssen die Periodenwerte gleichmäßig verteilt und dann wie unten gezeigt in Skalenwerte umgewandelt werden :):

Auflistung

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #  CWT  ,       cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bboxf = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowpropsf = dict(facecolor='yellow', shrink=0.05) text = ax.annotate("unusual\nfeature", xy=(365*6, 15), xytext=(365*3, 50), bbox=bboxf, arrowprops=arrowpropsf) show()

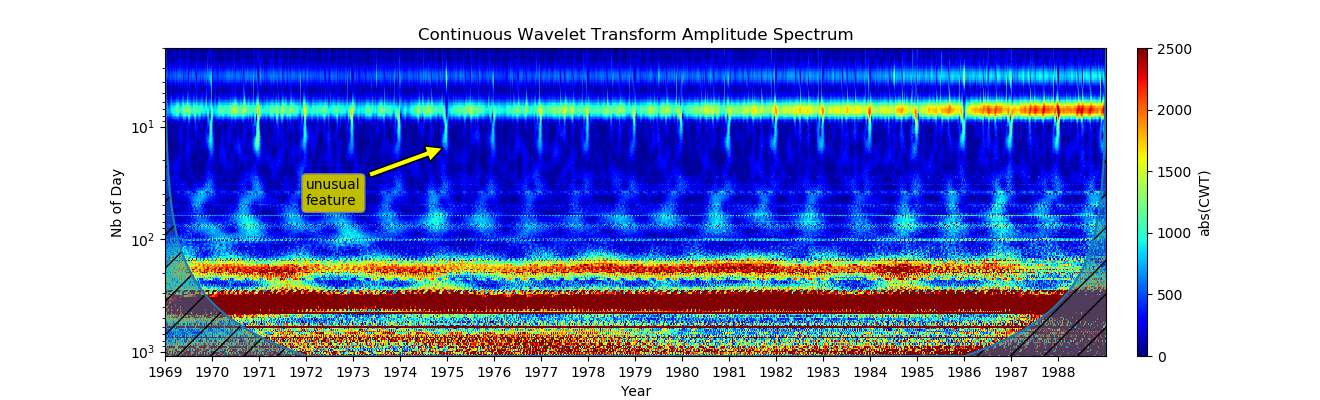
Wir können Signaländerungen auf allen Skalen sehen. Das Sialogramm zeigt jedes Jahr in gleichen Zeiträumen.

6. Hervorheben eines Teils der Zeitleiste (Suchen nach Zwischendaten zwischen den Zeitleistenmarkierungen auf der Suche nach Artefakten oder fehlenden Daten.):

Auflistung

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) #    : 1974-1976 fig = figure(figsize=(12,4)) lines =plot(births.index, births.values/1000, '-') xlim(pd.to_datetime("1974-01-01"), pd.to_datetime("1976-01-01")) ylabel("Nb of birthes [k]"); title("Total births per day bw 1974 and 1976"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1974-1969)*365, (1976-1969)*365 ) show()

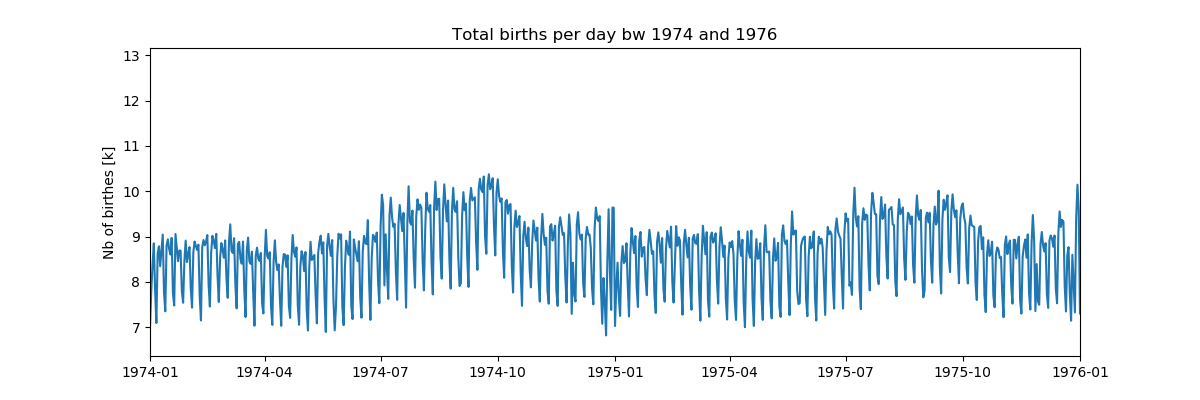
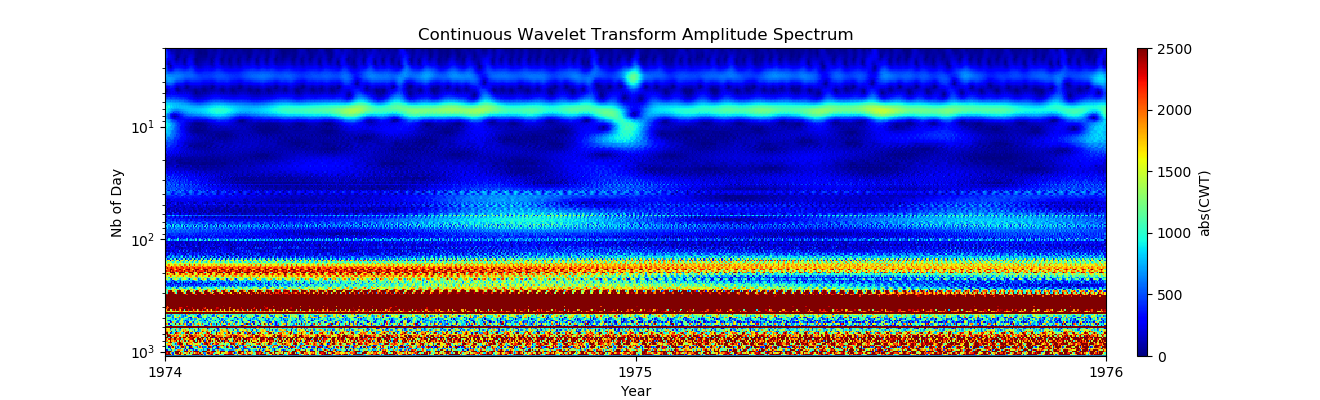Auf den ersten Blick sehen die wöchentlichen Muster sehr gleichmäßig aus, aber am Weihnachtstag passiert etwas. Schauen wir uns diesen Zeitraum noch einmal an:

Auflistung

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) # :  1975    1976  fig = figure(figsize=(12,4)) lines = plot(births.index, births.values/1000, '.-') xlim(pd.to_datetime("1974-12-01"), pd.to_datetime("1975-02-01")) ylabel("Nb of birthes [k]"); title("Total births per day : 2 monthes zoom"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1975-1969)*365-30, (1975-1969)*365+30 ) show()

Jetzt ist klar, dass dies der Effekt des Jahresendes ist:

Weihnachten: Der 23./24. Dezember zeigt eine ungewöhnlich geringe Anzahl von Geburten, und diese Tage weichen heutzutage vom Wochenplan ab.
Es gibt Daten für Dezember, die mit dem Vorhandensein eines gewissen Werts für die betroffenen Daten am 1. und 2. Januar übereinstimmen. Diese Daten sind normalerweise kleiner als persönliche Ereignisse

7. Synthese (Ein Sialogramm wird aus normalisierten Daten mit besserer Lesbarkeit für alle Skalen erstellt):

Auflistung

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bbox = dict(boxstyle="round", facecolor="w", edgecolor="0.5") bbox2 = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowprops = dict(facecolor='white', shrink=0.05) arrowprops2 = dict(facecolor='yellow', shrink=0.05) for period, label in [ (3.5, "half a week"), (7, "one week"), (365/2, "half a year"), (365, "one year"), (365*2.8, "long trends")]: text = ax.annotate(label, xy=(365*5.5, period), xytext=(365*2, period), bbox=bbox, arrowprops=arrowprops) text = ax.annotate("end of year\neffect", xy=(365*6, 15), xytext=(365*3, 50), bbox=bbox2, arrowprops=arrowprops2) text = ax.annotate("increase in\nvariations *amplitude*", xy=(365*18.5, 7), xytext=(365*14, 50), bbox=bbox2, arrowprops=arrowprops2) show()

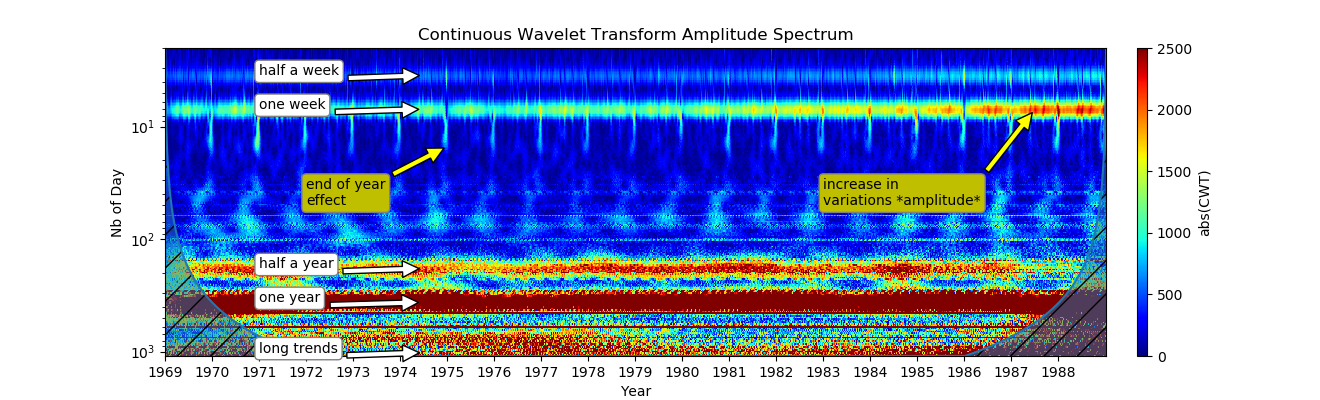CWT enthüllt in kurzer Zeit viele Informationen:

Eine wöchentliche Variation, die die Krankenhausgewohnheiten zeigt, ist seit mehreren Jahrzehnten vorhanden;

In den 80er Jahren gab es einen Anstieg des wöchentlichen Indikators, der durch eine Änderung der Arbeitsgewohnheiten von Krankenhäusern, eine Änderung der Fruchtbarkeit oder eine einfache Änderung der Bevölkerung verursacht werden kann.

Die zweite Halbjahresband ist eindeutig die zweite Harmonische. In der Zone von 3 bis 1 Monat treten unscharfe Muster auf, was auf die dritte Harmonische zurückzuführen sein kann, da die jährlichen Schwankungen so stark sind. Es kann auch durch die Auswirkung von Feiertagen auf die Fruchtbarkeit verursacht werden und weitere Untersuchungen erfordern;

Die Auswirkungen des Jahresendes wurden an Weihnachten und am 1. Januar festgestellt. Dieser kann bei einer anderen Frequenzmethode unsichtbar geblieben sein.

Schlussfolgerungen:

In dieser Veröffentlichung haben wir gesehen, wie sich die Grundform von Signalvariationen in ein Skalogramm umsetzt. Ein Beispiel eines zeitlich geordneten Datensatzes wurde dann verwendet, um Schritt für Schritt zu demonstrieren, wie CWT auf Standarddaten angewendet wird.

Die obige Technik kann erweitert werden, um den Netzwerkverkehr zu analysieren und ungewöhnliches Verhalten von Objekten zu erkennen. CWT ist ein leistungsstarkes Tool, das zunehmend als Eingabe für neuronale Netze verwendet wird und zur Erstellung neuer Funktionen zur Klassifizierung oder Erkennung von Anomalien verwendet werden kann.

Jedes Beispiel ist als eigenständiges Programm implementiert, mit dem Sie ein Beispiel für Ihre Aufgabe auswählen können, ohne auf die vorherigen und nachfolgenden Beispiele eingehen zu müssen. Der Benutzer kann beliebige Wavelet-Funktionen aus der am Anfang jedes Programms angegebenen Liste ausprobieren, z. B. mexh oder gaus5. Zum Beispiel 1:

PS Für die praktische Verwendung von Auflistungen werde ich die Versionen der darin verwendeten Module angeben:

 >>> import scaleogram; print(scaleogram .__version__) 0.9.5 >>> import pandas; print(pandas .__version__) 0.24.1 >>> import numpy; print(numpy .__version__) 1.16.1 >>> import matplotlib; print(matplotlib .__version__) 3.0.2

Für einen unabhängigen Datensatz in der * .csv-Datei bringe ich die Datenstruktur (in einer Spalte):
Jahr, Monat, Tag, Geschlecht, Geburten
1969,1,1, F, 4046
1969,1,1, M, 4440
1969,1,2 F, 4454,
1969.1.2, M, 4548
...
Für Pandas der Version 0.24.1 müssen Sie Matplotlib-Konverter explizit registrieren.

So registrieren Sie Konverter:

 from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()

Wavelet-Analyse. Teil 3

Einführung

Wavelet - Einfache Signalskalogramme

Wavelet-Skalogramme von Spezialsignalen

Wavelet-Timeline-Skalogramme

Schlussfolgerungen:

More articles: