Was ist das beste Werkzeug zum Zeichnen von Vektorbildern? Für mich und wahrscheinlich für viele andere ist die Antwort ziemlich offensichtlich: Illustrator oder vielleicht Inkscape. Zumindest dachte ich das, als ich gebeten wurde, ungefähr achthundert Diagramme für ein Physiklehrbuch zu zeichnen. Nichts Außergewöhnliches, nur ein paar Schwarz-Weiß-Illustrationen mit Kugeln, Federn, Riemenscheiben, Linsen und so weiter. Zu diesem Zeitpunkt war bereits bekannt, dass das Buch in LaTeX erstellt werden sollte, und ich erhielt eine Reihe von MS Word-Dokumenten mit eingebetteten Bildern. Einige von ihnen waren gescannte Bilder aus anderen Büchern, andere waren Bleistiftzeichnungen. Als ich mir Tage und Nächte vorstellte, in denen ich dieses Zeug mit Tinte bedeckte, wurde mir schwindelig, und so stellte ich mir bald vor, ich würde mir eine automatisiertere Lösung vorstellen. Aus irgendeinem Grund wurde
MetaPost zum Mittelpunkt dieser Fantasien.
Der Hauptvorteil der Verwendung von MetaPost (oder einer ähnlichen) Lösung besteht darin, dass jedes Bild eine Art Funktion mehrerer Variablen sein kann. Ein solches Bild kann schnell an unvorhergesehene Umstände des Layouts angepasst werden, ohne wichtige interne Beziehungen der Abbildung zu stören (worüber ich mir wirklich Sorgen gemacht habe), was mit herkömmlichen Werkzeugen nicht einfach zu erreichen ist. Auch wiederkehrende Elemente, all diese Kugeln und Federn, können optisch interessanter gemacht werden, als dies herkömmliche Werkzeuge bei gleichen zeitlichen Einschränkungen zulassen würden.
Ich wollte Bilder mit einer Art Schraffur machen, ähnlich wie in alten Büchern.

Zuerst musste ich in der Lage sein, einige Kurven unterschiedlicher Dicke zu erzeugen. Die Hauptkomplikation besteht darin, eine Kurve zu konstruieren, die der ursprünglichen Kurve in unterschiedlichem Abstand folgt. Ich habe wahrscheinlich die primitivste Arbeitsmethode
verwendet , die darauf hinausläuft, die Liniensegmente, die die Bezier-Kurvenkontrollpunkte verbinden, einfach um einen bestimmten Abstand zu verschieben, außer dass dieser Abstand entlang der Kurve variiert.

In den meisten Fällen hat es gut funktioniert.

BeispielcodeAb hier wird davon ausgegangen, dass die Bibliothek
heruntergeladen und
input fiziko.mp; ist im MetaPost-Code vorhanden. Die schnellste Methode ist die Verwendung von ConTeXt (dann benötigen Sie weder
beginfig endfig ):
\starttext
\startMPcode
input fiziko.mp;
% the code goes here
\stopMPcode
\stoptext
oder LuaLaTeX:
\documentclass{article}
\usepackage{luamplib}
\begin{document}
\begin{mplibcode}
input fiziko.mp;
% the code goes here
\end{mplibcode}
\end{document}
beginfig(3);
path p, q; % MetaPost's syntax is reasonably readable, so I'll comment mostly on my stuff
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q := offsetPath(p)(1cm*sin(offsetPathLength*pi)); % first argument is the path itself, second is a function of the position along this path (offsetPathLength changes from 0 to 1), which determines how far the outline is from the original line
draw p;
draw q dashed evenly;
endfig;
Zwei Umrisse können kombiniert werden, um eine Konturlinie für einen Strich mit variabler Dicke zu erstellen.

Beispielcodebeginfig(4);
path p, q[];
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q1 := offsetPath(p)(1/2pt*(sin(offsetPathLength*pi)**2)); % outline on one side
q2 := offsetPath(p)(-1/2pt*(sin(offsetPathLength*pi)**2)); % and on the other
fill q1--reverse(q2)--cycle;
endfig;
Die Linienstärke sollte eine Untergrenze haben, andernfalls sind einige Linien zu dünn, um richtig gedruckt zu werden, und dies sieht nicht gut aus. Eine der Optionen (die ich gewählt habe) besteht darin, die zu dünnen Linien gestrichelt zu machen, so dass die Gesamtmenge an Tinte pro Längeneinheit ungefähr gleich bleibt wie in der beabsichtigten dünneren Linie. Mit anderen Worten, anstatt die Tintenmenge an den Seiten der Linie zu verringern, entnimmt der Algorithmus etwas Tinte aus der Linie selbst.

Beispielcodebeginfig(5);
path p;
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
draw brush(p)(1pt*(sin(offsetPathLength*pi)**2)); % the arguments are the same as for the outline
endfig;
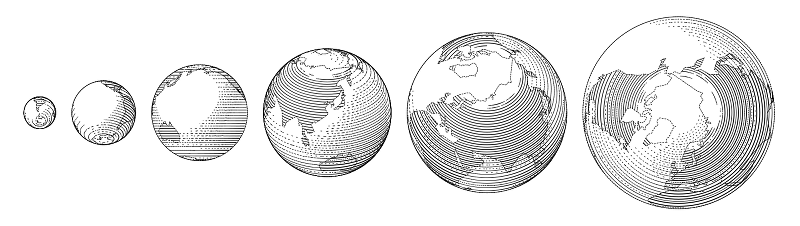
Sobald Sie Linien mit variabler Dicke bearbeitet haben, können Sie Kugeln zeichnen. Eine Kugel kann als eine Reihe konzentrischer Kreise dargestellt werden, wobei die Liniendicken je nach Ausgabe einer Funktion variieren, die die Helligkeit eines bestimmten Punkts auf der Kugel berechnet.

Beispielcodebeginfig(6);
draw sphere.c(1.2cm);
draw sphere.c(2.4cm) shifted (2cm, 0);
endfig;
Ein weiterer praktischer Baustein ist eine „Röhre“. Grob gesagt ist es ein Zylinder, den man biegen kann. Solange der Durchmesser konstant ist, ist es ziemlich einfach.

Beispielcodebeginfig(7);
path p;
p := subpath (1,8) of fullcircle scaled 3cm;
draw tube.l(p)(1/2cm); % arguments are the path itself and the tube radius
endfig;
Wenn der Durchmesser nicht konstant ist, werden die Dinge komplizierter: Die Anzahl der Striche sollte sich entsprechend der Rohrdicke ändern, um die Tintenmenge pro Flächeneinheit konstant zu halten, bevor die Lichter berücksichtigt werden.
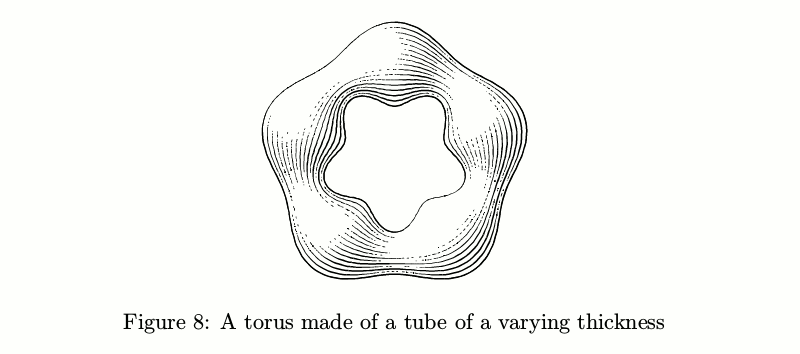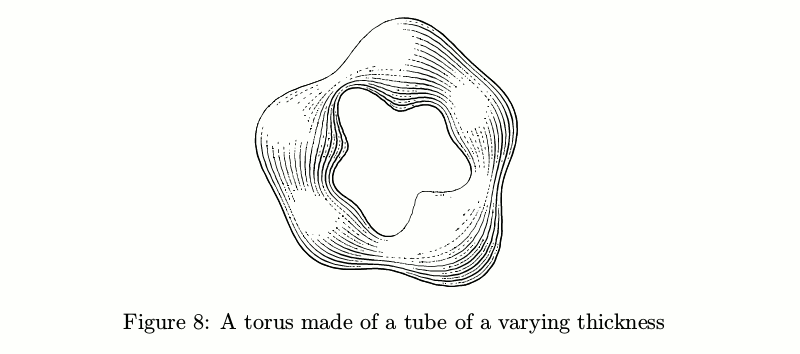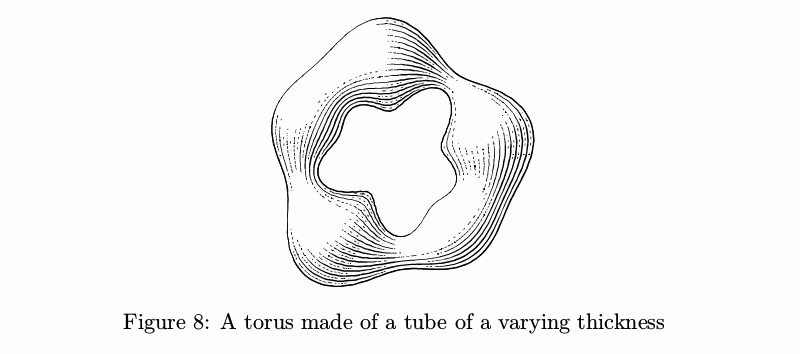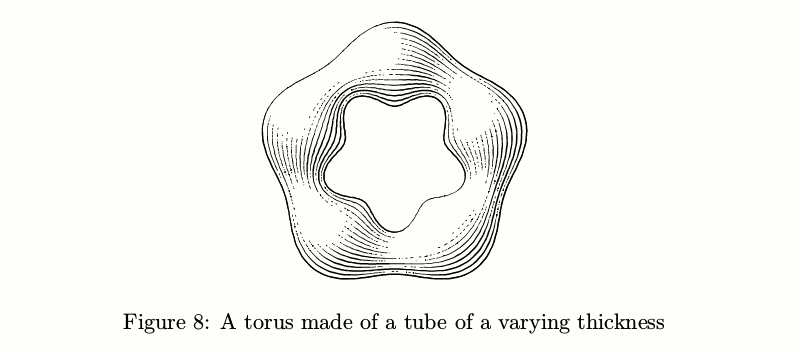
Beispielcodebeginfig(8);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm; % this thing splits every segment between the points of a path (here—fullcircle) into several parts (here—2)
draw tube.l(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Es gibt auch Rohre mit Querschraffur. Das Problem, die Tintenmenge konstant zu halten, stellte sich in diesem Fall als noch schwieriger heraus, so dass solche Röhren oft etwas zottelig aussehen.

Beispielcodebeginfig(9);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.t(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Mit Rohren kann eine Vielzahl von Objekten konstruiert werden: von Kegeln und Zylindern bis hin zu Balustern.

Beispielcodebeginfig(10);
draw tube.l ((0, 0) -- (0, 3cm))((1-offsetPathLength)*1cm) shifted (-3cm, 0); % a very simple cone
path p;
p := (-1/2cm, 0) {dir(175)} .. {dir(5)} (-1/2cm, 1/8cm) {dir(120)} .. (-2/5cm, 1/3cm) .. (-1/2cm, 3/4cm) {dir(90)} .. {dir(90)}(-1/4cm, 9/4cm){dir(175)} .. {dir(5)}(-1/4cm, 9/4cm + 1/5cm){dir(90)} .. (-2/5cm, 3cm); % baluster's envelope
p := pathSubdivide(p, 6);
draw p -- reverse(p xscaled -1) -- cycle;
tubeGenerateAlt(p, p xscaled -1, p rotated -90); % a more low-level stuff than tube.t, first two arguments are tube's sides and the third is the envelope. The envelope is basically a flattened out version of the outline, with line length along the x axis and the distance to line at the y. In the case of this baluster, it's simply its side rotated 90 degrees.
endfig;
Einige Konstruktionen, die aus diesen Grundelementen hergestellt werden können, sind in der Bibliothek enthalten. Zum Beispiel ist der Globus im Grunde eine Kugel.

Beispielcodebeginfig(11);
draw globe(1cm, -15, 0) shifted (-6/2cm, 0); % radius, west longitude, north latitude, both decimal
draw globe(3/2cm, -30.280577, 59.939461);
draw globe(4/3cm, -140, -30) shifted (10/3cm, 0);
endfig;
Die Schraffur ist hier jedoch in Breitenrichtung und die Steuerung der Liniendichte ist viel schwieriger als bei normalen Kugeln mit „konzentrischer“ Schraffur, sodass es sich um eine andere Art von Kugel handelt.

Beispielcodebeginfig(12);
draw sphere.l(2cm, -60); % diameter and latitude
draw sphere.l(3cm, 45) shifted (3cm, 0);
endfig;
Ein Gewicht ist eine einfache Konstruktion aus Rohren zweier Typen.

Beispielcodebeginfig(13);
draw weight.s(1cm); % weight height
draw weight.s(2cm) shifted (2cm, 0);
endfig;
Es gibt auch ein Werkzeug zum Verknoten der Rohre.

Beispielcode. Der Kürze halber nur ein Knoten.beginfig(14);
path p;
p := (dir(90)*4/3cm) {dir(0)} .. tension 3/2 ..(dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2 ..(dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2 .. cycle;
p := p scaled 6/5;
addStrandToKnot (primeOne) (p, 1/4cm, "l", "1, -1, 1"); % first, we add a strand of width 1/4cm going along the path p to the knot named primeOne. its intersections along the path go to layers "1, -1, 1" and the type of tube is going to be "l".
draw knotFromStrands (primeOne); % then the knot is drawn. you can add more than one strand.
endfig;
Röhren in Knoten werfen Schatten aufeinander, wie sie sollten. Theoretisch kann diese Funktion in anderen Kontexten verwendet werden, aber da ich nicht vorhatte, tief in die dritte Dimension einzudringen, fehlt die Benutzeroberfläche etwas und Schatten funktionieren nur für einige Objekte ordnungsgemäß.

Beispielcodebeginfig(15);
path shadowPath[];
boolean shadowsEnabled;
numeric numberOfShadows;
shadowsEnabled := true; % shadows need to be turned on
numberOfShadows := 1; % number of shadows should be specified
shadowPath0 := (-1cm, -2cm) -- (-1cm, 2cm) -- (-1cm +1/6cm, 2cm) -- (-1cm + 1/8cm, -2cm) -- cycle; % shadow-dropping object should be a closed path
shadowDepth0 := 4/3cm; % it's just this high above the object on which the shadow falls
shadowPath1 := shadowPath0 rotated -60;
shadowDepth1 := 4/3cm;
draw sphere.c(2.4cm); % shadows work ok only with sphere.c and tube.l with constant diameter
fill shadowPath0 withcolor white;
draw shadowPath0;
fill shadowPath1 withcolor white;
draw shadowPath1;
endfig;
Natürlich benötigen Sie eine Holzstruktur (Update: Seit die russische Version dieses Artikels veröffentlicht wurde, ist der erste Fall, dass diese Bibliothek in einem realen Projekt verwendet wird, von dem ich weiß, dass
es aufgetreten ist , und es war die Holzstruktur, die kam praktisch, so dass dies doch kein Scherz war). Wie Zweige und ihr Wachstum das Muster der Jahresringe beeinflussen, ist ein Thema für einige ernsthafte Studien. Das einfachste Arbeitsmodell, das ich mir vorstellen kann, lautet wie folgt: Jahresringe sind parallele flache Oberflächen, die durch wachsende Zweige verzerrt sind; Daher wird die Oberfläche durch eine Reihe nicht übermäßig komplexer „Zweigfunktionen“ an verschiedenen Stellen modifiziert, und die Isolinien der Oberfläche werden als Jahresringmuster verwendet.

Beispielcodebeginfig(16);
numeric w, b;
pair A, B, C, D, A', B', C', D';
w := 4cm;
b := 1/2cm;
A := (0, 0);
A' := (b, b);
B := (0, w);
B' := (b, wb);
C := (w, w);
C' := (wb, wb);
D := (w, 0);
D' := (wb, b);
draw woodenThing(A--A'--B'--B--cycle, 0); % a piece of wood inside the A--A'--B'--B--cycle path, with wood grain at 0 degrees
draw woodenThing(B--B'--C'--C--cycle, 90);
draw woodenThing(C--C'--D'--D--cycle, 0);
draw woodenThing(A--A'--D'--D--cycle, 90);
eyescale := 2/3cm; % scale for the eye
draw eye(150) shifted 1/2[A,C]; % the eye looks in 150 degree direction
endfig;
Das Auge aus dem Bild oben öffnet sich weit oder blinzelt ein wenig und seine Pupille ändert auch seine Größe. Es mag praktisch keinen Sinn ergeben, aber mechanisch ähnliche Augen sehen einfach langweilig aus.

Beispielcodebeginfig(17);
eyescale := 2/3cm; % 1/2cm by default
draw eye(0) shifted (0cm, 0);
draw eye(0) shifted (1cm, 0);
draw eye(0) shifted (2cm, 0);
draw eye(0) shifted (3cm, 0);
draw eye(0) shifted (4cm, 0);
endfig;
Meistens waren die Illustrationen nicht allzu komplex, aber für einen strengeren Ansatz müssten viele der Probleme im Lehrbuch gelöst werden, um sie korrekt zu veranschaulichen. Sagen wir, L'Hôpitals Problem mit der Riemenscheibe (es war nicht in diesem Lehrbuch, aber trotzdem): am Seil mit der Länge
an der Stelle aufgehängt
eine Riemenscheibe hängt; Es ist an einem anderen Seil befestigt, das an der Spitze aufgehängt ist
mit dem Gewicht
am Ende. Die Frage ist: Wohin geht das Gewicht, wenn sowohl die Riemenscheibe als auch die Seile nichts wiegen? Überraschenderweise sind die Lösung und der Aufbau für dieses Problem nicht so einfach. Wenn Sie jedoch mit mehreren Variablen spielen, können Sie das Bild unter Beibehaltung der Genauigkeit genau richtig für die Seite aussehen lassen.

Beispielcodevardef lHopitalPulley (expr AB, l, m) = % distance AB between the suspension points of the ropes and their lengths l and m. “Why no units of length?”, you may ask. It's because some calculations inside can cause arithmetic overflow in MetaPost.
save A, B, C, D, E, o, a, x, y, d, w, h, support;
image(
pair A, B, C, D, E, o[];
path support;
numeric a, x[], y[], d[], w, h;
x1 := (l**2 + abs(l)*((sqrt(8)*AB)++l))/4AB; % the solution
y1 := l+-+x1; % second coordinate is trivial
y2 := m - ((AB-x1)++y1); % as well as the weight's position
A := (0, 0);
B := (AB*cm, 0);
D := (x1*cm, -y1*cm);
C := D shifted (0, -y2*cm);
d1 := 2/3cm; d2 := 1cm; d3 := 5/6d1; % diameters of the pulley, weight and the pulley wheel
w := 2/3cm; h := 1/3cm; % parameters of the wood block
o1 := (unitvector(CD) rotated 90 scaled 1/2d3);
o2 := (unitvector(DB) rotated 90 scaled 1/2d3);
E := whatever [D shifted o1, C shifted o1]
= whatever [D shifted o2, B shifted o2]; % pulley's center
a := angle(AD);
support := A shifted (-w, 0) -- B shifted (w, 0) -- B shifted (w, h) -- A shifted (-w, h) -- cycle;
draw woodenThing(support, 0); % wood block everything is suspended from
draw pulley (d1, a - 90) shifted E; % the pulley
draw image(
draw A -- D -- B withpen thickpen;
draw D -- C withpen thickpen;
) maskedWith (pulleyOutline shifted E); % ropes should be covered with the pulley
draw sphere.c(d2) shifted C shifted (0, -1/2d2); % sphere as a weight
dotlabel.llft(btex $A$ etex, A);
dotlabel.lrt(btex $B$ etex, B);
dotlabel.ulft(btex $C$ etex, C);
label.llft(btex $l$ etex, 1/2[A, D]);
)
enddef;
beginfig(18);
draw lHopitalPulley (6, 2, 11/2); % now you can choose the right parameters
draw lHopitalPulley (3, 5/2, 3) shifted (8cm, 0);
endfig;
Und was ist mit dem Lehrbuch? Leider passierte etwas und das Lehrbuch wurde abgebrochen, als fast alle Illustrationen und das Layout fertig waren. Vielleicht habe ich mich deshalb entschlossen, die meisten Funktionen der Originalbibliothek von Grund auf neu zu schreiben (ich habe mich dafür entschieden, keinen der Originalcodes zu verwenden, für die ich, obwohl indirekt, bezahlt wurde) und
ihn auf GitHub zu stellen . Einige Dinge, die in der Originalbibliothek vorhanden sind, wie Funktionen zum Zeichnen von Autos und Traktoren, habe ich dort nicht aufgenommen, einige neue Funktionen, z. B. Knoten, wurden hinzugefügt.
Es läuft nicht schnell: Es dauert ungefähr eine Minute, um alle Bilder für diesen Artikel mit LuaLaTeX auf meinem Laptop mit i5-4200U 1,6 GHz zu produzieren. Hier und da wird ein Pseudozufallszahlengenerator verwendet, sodass keine zwei ähnlichen Bilder absolut identisch sind (das ist eine Funktion) und jeder Lauf leicht unterschiedliche Bilder erzeugt. Um Überraschungen zu vermeiden, können Sie einfach
randomseed := some number und bei jedem Lauf die gleichen Ergebnisse erzielen.
Vielen Dank an
Dr. Ord und
Mikael Sundqvist für ihre Hilfe bei der englischen Version dieses Textes.