ARA: Algorithmus zum Ermitteln der maximalen Anzahl von Punkten auf einer geraden Linie

Kürzlich bin ich auf ein klassisches Problem bei Interviews gestoßen: Suche nach der maximalen Anzahl von Punkten, die auf einer geraden Linie stehen (in einer Ebene, ganzzahlige Koordinaten). Die Idee einer erschöpfenden Suche kam mir sofort in den Sinn, die in O (n ^ 2) eine offensichtliche zeitliche Komplexität aufweist, aber es schien mir, dass es etwas anderes geben sollte, zumindest eine Alternative in O (n * log (n)). . Nach einer halben Stunde wurde noch etwas Besseres gefunden!



_{Eine detailliertere Darstellung des Problems mit Beispielen für Eingabe / Ausgabe finden Sie in GeeksForGeeks und LeetCode}

Zuerst habe ich festgestellt, dass Sie das Problem nur für horizontale oder vertikale Linien leicht lösen können, indem Sie das X / Y jedes Punkts im Wörterbuch hinzufügen. Und was ist der Unterschied zwischen den anderen Zeilen? Nur ein Hang? .. Aber es ist reparabel!

Daher habe ich beschlossen, dass es möglich ist, die gesamte Liste der Punkte mehrmals durch Drehen zu durchlaufen. Und die Lösung in O (n) wird erhalten! Obwohl mit einem großen Koeffizienten. Ich hoffe wirklich, dass ich kein Fahrrad erfunden habe :)

# ***  *** #   #    = 180/ROT_COUNT  # #      12, #  180*4    (6% ), #  180*20   (0% ). # ó    . #     - . ROT_COUNT = 180*10 #  #        , #       1 / MULT_COEF. #    4  . #   MULT_COEF   ROT_COUNT. # ó    - . #     - . MULT_COEF = 2 ** 3 angles = list(map(lambda x: x*180.0/ROT_COUNT, range(ROT_COUNT))) def mnp_rotated(points, angle): """Returns Maximum Number of Points on the same line with given rotation""" #   rad = math.radians(angle) co = math.cos(rad) si = math.sin(rad) #      counts = {} for pair in points: #    nx = pair[0]*co - pair[1]*si #       , #      #       #      nx = int(nx * MULT_COEF) #   if nx in counts: counts[nx] += 1 else: counts[nx] = 1 #    return max(counts.values()) def mnp(points): """Returns Maximum Number of Points on the same line""" res = 0 best_angle = 0 #      for i in angles: current = mnp_rotated(points, i) #  ,     if current > res: res = current best_angle = i return res 

Visualisiert sieht es ungefähr so ​​aus:
_{mein erstes hausgemachtes GIF, bitte nicht schelten :)}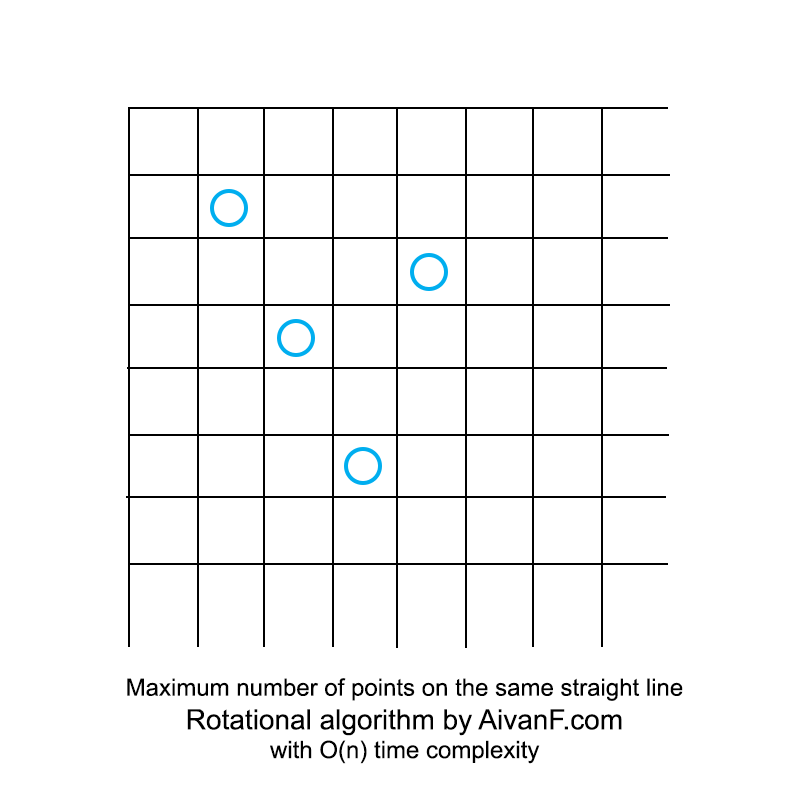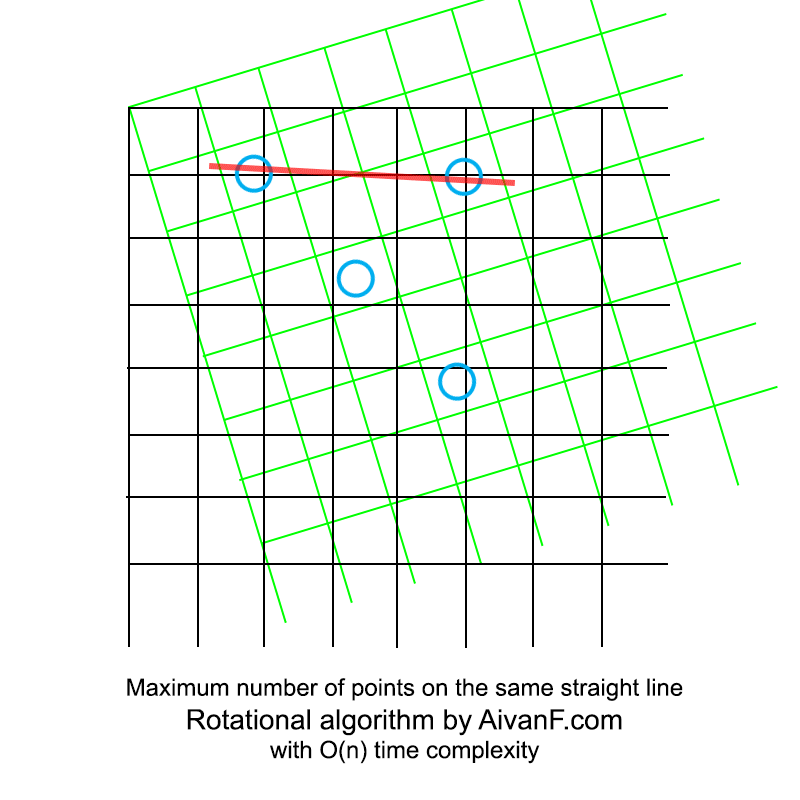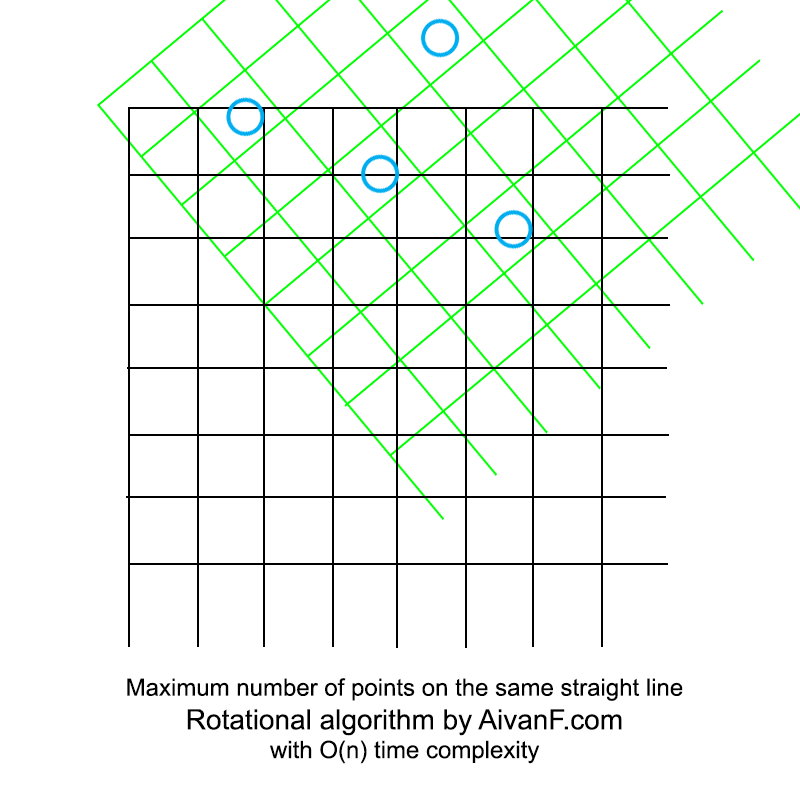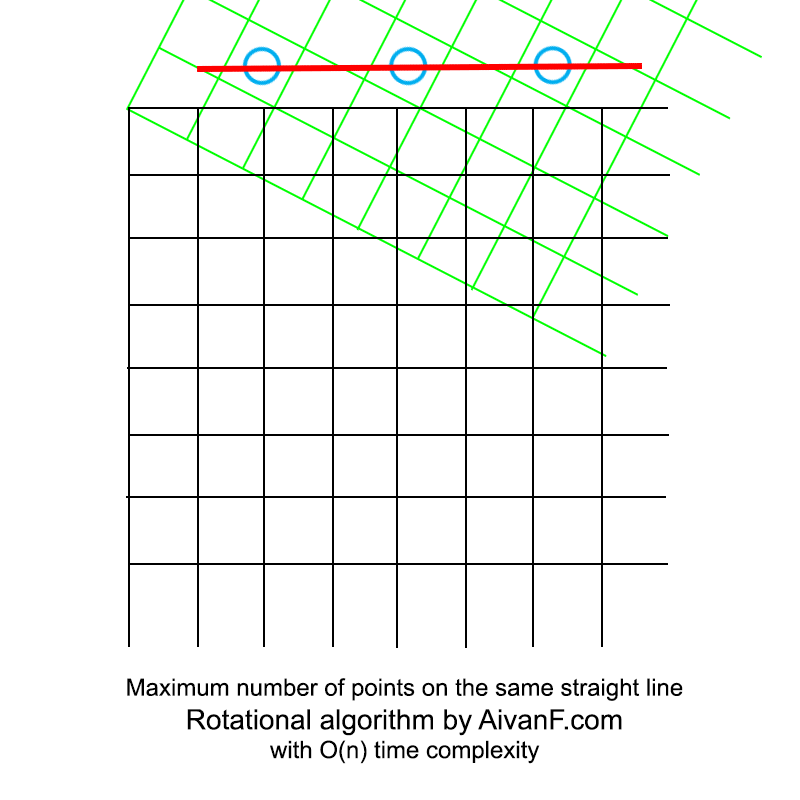



Es ist interessant festzustellen, dass die nachfolgende Implementierung einer umfassenden Suche mehr Codezeilen in Anspruch nahm.

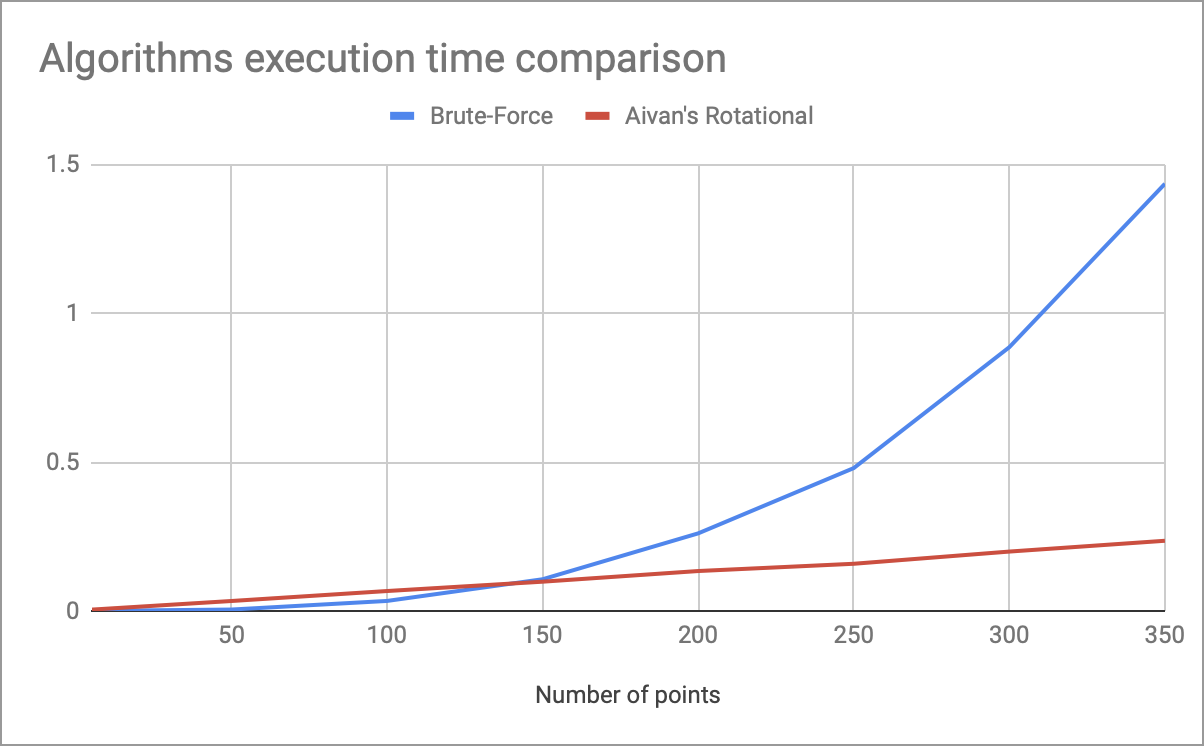
Das Diagramm mit Messungen der Laufzeit meines Rotationsalgorithmus und vollständiger Aufzählung in Abhängigkeit von der Anzahl der Punkte befindet sich in der Kopfzeile.


Ungefähr 150 Punkte zeigen den Vorteil der linearen Komplexität in der Zeit (mit den im obigen Code verwendeten Koeffizienten). Infolgedessen weist dieser Algorithmus die folgenden Nachteile auf:

• Die Genauigkeit ist nicht absolut.
• Die Laufzeit für kleine Punktmengen ist lang.
  _{Im Allgemeinen kann dies durch eine kompetente Auswahl von Koeffizienten leicht korrigiert werden: Für einfache Mengen ist ROT_COUNT = 36 anstelle von 2000 völlig ausreichend, was den Code mehr als 50-mal beschleunigt.}

Und solche Vorteile:

• Es arbeitet ruhig mit Bruchkoordinaten.
• Die zeitliche Komplexität ist linear, was sich bei großen Datenmengen bemerkbar macht.

Eine Tabelle mit Maßen finden Sie hier . Der gesamte Quellcode des Projekts mit beiden Algorithmen und verschiedenen Überprüfungen befindet sich auf dem GitHub .

Update Ich möchte noch einmal darauf hinweisen, dass dieser Algorithmus sowohl Vor- als auch Nachteile hat. Ich befürworte ihn nicht als idealen Ersatz für Brute Force. Ich habe gerade eine interessante mögliche Alternative beschrieben, die in einigen Fällen geeigneter sein kann.