
Um einen Nicht-Programm-Solver für Python zu erstellen, schreiben Sie ihn in Rust um, um ihn über WebAssembly direkt im Browser auszuführen.
TL; DR
Starten Sie
Über japanische Kreuzworträtsel (Nonogramme) auf dem Habré gab es bereits mehrere Beiträge. Beispiel
und noch eine .
Bilder werden mit Zahlen verschlüsselt, die sich links neben den Zeilen sowie über den Spalten befinden. Die Anzahl der Zahlen gibt an, wie viele Gruppen schwarzer Zellen (oder deren Farbe für Farbkreuzworträtsel) in der entsprechenden Zeile oder Spalte enthalten sind, und die Zahlen selbst - wie viele zusammengeführte Zellen jede dieser Gruppen enthält (z. B. eine Reihe von drei Zahlen - 4, 1 und 3) bedeutet, dass es in dieser Zeile drei Gruppen gibt: die erste - von vier, die zweite - von einer, die dritte - von drei schwarzen Zellen). In einem Schwarz-Weiß-Kreuzworträtsel müssen die Gruppen durch mindestens eine leere Zelle getrennt sein. Im Farbkreuzworträtsel gilt diese Regel nur für einfarbige Gruppen, und mehrfarbige Gruppen können eng beieinander liegen (leere Zellen können sich auch entlang der Ränder der Zeilen befinden). Es ist notwendig, den Ort der Zellgruppen zu bestimmen.
Eine der am weitesten verbreiteten Gesichtspunkte ist, dass nur diejenigen, die auf "logische" Weise gelöst werden, als "richtige" Kreuzworträtsel bezeichnet werden können. Dies wird normalerweise als Lösungsmethode bezeichnet, bei der Abhängigkeiten zwischen verschiedenen Zeilen und / oder Spalten nicht berücksichtigt werden. Mit anderen Worten, eine Lösung ist eine Folge unabhängiger Entscheidungen einzelner Zeilen oder Spalten, bis alle Zellen gefüllt sind (mehr zum Algorithmus unten). Beispielsweise finden Sie auf der Website http://nonograms.org/ ( http://nonograms.ru/ ) nur solche Nichtogramme. Nonogramme von dieser Site wurden bereits als Beispiel im Artikel Lösen japanischer Farbkreuzworträtsel mit Lichtgeschwindigkeit angeführt. Zu Vergleichs- und Überprüfungszwecken hat mein Solver auch Unterstützung für das Herunterladen und Parsen von Kreuzworträtseln von dieser Site hinzugefügt (danke an KyberPrizrak für die Erlaubnis, Materialien von seiner Site zu verwenden).
Das Konzept der Nichtogramme kann jedoch auf ein allgemeineres Problem erweitert werden, wenn die übliche "logische" Methode zu einer Sackgasse führt. In solchen Fällen muss man eine Annahme über die Farbe einer Zelle machen und nach dem Nachweis, dass diese Farbe zu einem Widerspruch führt, die entgegengesetzte Farbe für diese Zelle markieren. Die Abfolge solcher Schritte kann (wenn Sie die Geduld haben) uns alle Lösungen geben. In diesem Artikel geht es hauptsächlich um die Lösung eines solchen allgemeineren Falles von Kreuzworträtseln.
Python
Vor ungefähr anderthalb Jahren bin ich versehentlich auf einen Artikel gestoßen, in dem eine Methode zum Lösen einer einzelnen Zeile beschrieben wurde (wie sich später herausstellte, war die Methode ziemlich langsam).
Als ich diese Methode in Python (meiner Hauptarbeitssprache) implementierte und eine sequentielle Aktualisierung aller Zeilen hinzufügte, stellte ich fest, dass all dies nicht sehr schnell gelöst wurde. Nach dem Studium des Materials stellte sich heraus, dass es zu diesem Thema viele Arbeiten und Implementierungen gibt, die unterschiedliche Ansätze für diese Aufgabe bieten.
Es schien mir, dass die ehrgeizigste Arbeit an der Analyse verschiedener Solver-Implementierungen von Jan Wolter durchgeführt wurde, der auf seiner Website (die meines Wissens das größte öffentliche Repository für Nonogramme im Internet bleibt) eine detaillierte Studie mit einer Fülle von Informationen und Links veröffentlichte, die helfen können Erstellen Sie Ihren eigenen Löser.
Durch das Studium zahlreicher Quellen (sie werden am Ende des Artikels erscheinen) habe ich die Geschwindigkeit und Funktionalität meines Lösers schrittweise verbessert. Infolgedessen war ich süchtig und beschäftigte mich etwa 10 Monate lang in meiner Freizeit mit der Implementierung, dem Refactoring und dem Debuggen von Algorithmen.
Kernalgorithmen
Der resultierende Löser kann in Form von vier Entscheidungsebenen dargestellt werden:
( Linie ) linearer Löser: am Eingang eine Linie von Zellen und eine Beschreibungszeile (Hinweise), am Ausgang eine teilweise aufgelöste Linie. In der Python-Lösung habe ich 4 verschiedene Algorithmen implementiert (3 davon sind für Farbkreuzworträtsel angepasst). Der schnellste war der BguSolver-Algorithmus, der nach der ursprünglichen Quelle benannt wurde . Dies ist eine sehr effektive und praktisch standardmäßige Methode zum Lösen von Nicht-Programmzeichenfolgen mithilfe dynamischer Programmierung. Den Pseudocode dieser Methode finden Sie beispielsweise in diesem Artikel .
( Weitergabe ) Wir stellen alle Zeilen und Spalten in eine Warteschlange, gehen sie mit einem linearen Löser durch. Wenn wir beim Lösen einer Zeile (Spalte) neue Informationen erhalten, aktualisieren wir die Warteschlange jeweils mit neuen Spalten (Zeilen). Fahren Sie fort, bis die Zeile leer ist.
Beispiel und CodeWir übernehmen die nächste zu lösende Aufgabe aus der Warteschlange. Es sei eine leere (ungelöste) Zeichenkette der Länge 7 (wir bezeichnen sie als ??????? ) mit einer Beschreibung der Blöcke [2, 3] . Der lineare Löser erzeugt eine teilweise aufgelöste Zeichenfolge ?X??XX? Dabei ist X die gefüllte Zelle. Beim Aktualisieren der Zeile sehen wir, dass sich die Spalten mit den Nummern 1, 4, 5 geändert haben (die Indizierung beginnt bei 0). Dies bedeutet, dass neue Informationen in den angegebenen Spalten angezeigt wurden und an den „linearen“ Löser zurückgegeben werden können. Wir stellen diese Spalten in die Warteschlange der Aufgaben mit höherer Priorität (um sie als nächstes dem linearen Löser zu geben).
def propagation(board): line_jobs = PriorityDict() for row_index in range(board.height): new_job = (False, row_index) line_jobs[new_job] = 0 for column_index in range(board.width): new_job = (True, column_index) line_jobs[new_job] = 0 for (is_column, index), priority in line_jobs.sorted_iter(): new_jobs = solve_and_update(board, index, is_column) for new_job in new_jobs:
Für jede ungelöste Zelle sortieren wir alle Farboptionen und versuchen, sie mit diesen neuen Informationen zu verbreiten. Wenn wir einen Widerspruch bekommen, werfen wir diese Farbe aus den Farboptionen für die Zelle und versuchen, sie mithilfe der Ausbreitung erneut zu nutzen. Wenn es bis zum Ende gelöst ist, fügen wir die Lösung zur Liste der Lösungen hinzu, experimentieren jedoch weiterhin mit anderen Farben (es kann mehrere Lösungen geben). Wenn wir zu einer Situation kommen, in der es unmöglich ist, weiter zu lösen, ignorieren wir den Vorgang einfach und wiederholen ihn mit einer anderen Farbe / Zelle.
CodeGibt True zurück, wenn aufgrund der Stichprobe ein Widerspruch eingeht.
def probe(self, cell_state): board = self.board pos, assumption = cell_state.position, cell_state.color
( Backtracking ) Wenn Sie während der Prüfung ein teilweise gelöstes Rätsel nicht ignorieren, sondern weiterhin rekursiv dasselbe Verfahren aufrufen, erhalten wir ein Backtracking (mit anderen Worten, einen vollständigen Spaziergang in die Tiefe des potenziellen Entscheidungsbaums). Hier beginnt eine große Rolle zu spielen, welche der Zellen als nächste Erweiterung der möglichen Lösung ausgewählt wird. Gute Recherchen zu diesem Thema finden Sie in dieser Publikation .
CodeDas Zurückverfolgen ist für mich ziemlich chaotisch, aber diese beiden Funktionen beschreiben ungefähr, was während einer rekursiven Suche passiert
def search(self, search_directions, path=()): """ Return False if the given path is a dead end (no solutions can be found) """ board = self.board depth = len(path) save = board.make_snapshot() try: while search_directions: state = search_directions.popleft() assumption, pos = state.color, state.position cell_colors = board.cell_colors(pos) if assumption not in cell_colors: LOG.warning("The assumption '%s' is already expired. " "Possible colors for %s are %s", assumption, pos, cell_colors) continue if len(cell_colors) == 1: LOG.warning('Only one color for cell %r left: %s. Solve it unconditionally', pos, assumption) try: self._solve_without_search() except NonogramError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The path %s is invalid", assumption, pos, path) return False if board.is_solved_full: self._add_solution() LOG.warning( "The only color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True continue rate = board.solution_rate guess_save = board.make_snapshot() try: LOG.warning('Trying state: %s (depth=%d, rate=%.4f, previous=%s)', state, depth, rate, path) success = self._try_state(state, path) finally: board.restore(guess_save) if not success: try: LOG.warning( "Unset the color %s for cell '%s'. Solve it unconditionally", assumption, pos) board.unset_color(state) self._solve_without_search() except ValueError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The whole branch (depth=%d) is invalid. ", assumption, pos, depth) return False if board.is_solved_full: self._add_solution() LOG.warning( "The negation of color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True finally:
Also beginnen wir, unser Kreuzworträtsel ab der zweiten Ebene zu lösen (das erste ist nur für den entarteten Fall geeignet, wenn es im gesamten Kreuzworträtsel nur eine Zeile oder Spalte gibt) und bewegen uns schrittweise nach oben. Wie Sie vielleicht erraten haben, verursacht jedes Level mehrmals das zugrunde liegende Level. Für eine effektive Lösung ist es daher unerlässlich, schnelle erste und zweite Level zu haben, die für komplexe Rätsel millionenfach aufgerufen werden können.
In diesem Stadium stellt sich (eher erwartet) heraus, dass Python überhaupt nicht das Werkzeug ist, das für eine maximale Leistung bei einer derart CPU-intensiven Aufgabe geeignet ist: Alle darin enthaltenen Berechnungen sind im Vergleich zu Sprachen niedrigerer Ebenen äußerst ineffizient. Beispielsweise stellte sich heraus, dass der am meisten algorithmisch geschlossene BGU-Löser (in Java) laut Messergebnissen bei einer Vielzahl von Aufgaben 7-17 (manchmal bis zu 27) Mal schneller war.
Weitere Details pynogram_my BGU_my Beschleunigung
Tänzer 0,976 0,141 6,921986
Cat 1.064 0.110 9.672727
Skid 1.084 0.101 10.732673
Dollar 1.116 0.118 9.457627
Kante 1,208 0,094 12,851064
Rauch 1.464 0.120 12.200000
Knoten 1,332 0,140 9,514286
Swing 1.784 0.138 12.927536
Mutter 2.108 0.147 14.340136
DiCap 2.076 0.176 11.795455
Tragisch 2,368 0,265 8,935849
Merka 2,084 0,196 10,632653
Petro 2.948 0.219 13.461187
M & M 3,588 0,375 9,568000
Signiert 4.068 0.242 16.809917
Licht 3,848 0,488 7,885246
Für immer 111.000 13.570 8.179808
Center 5.700 0.327 17.431193
Hot 3.150 0.278 11.330935
Karate 2.500 0.219 11.415525
9-Dom 510.000 70.416 7.242672
Flagge 149.000 5.628 26.474769
Löwe 71.000 2.895 24.525043
Marley 12.108 4.405 2.748695
Sache 321.000 46.166 6.953169
Nature inf 433.138 inf
Sierp inf inf NaN
Gettys inf inf NaN
Die Messungen wurden an meinem Auto durchgeführt. Die Rätsel stammen aus dem Standard-Set, das Jan Wolter für seinen Vergleich verwendet hat
Und das ist bereits, nachdem ich angefangen habe, PyPy zu verwenden, und auf Standard-CPython war die Berechnungszeit 4-5 Mal länger als auf PyPy! Wir können sagen, dass die Leistung eines ähnlichen Java-Solvers 28-85-mal höher war als die des CPython-Codes.
Versuche, die Leistung meines Lösers mithilfe der Profilerstellung (cProfile, SnakeViz, line_profiler) zu verbessern, führten zu einer gewissen Beschleunigung, führten jedoch natürlich nicht zu einem unheimlichen Ergebnis.
+ Solver kann alle Rätsel auf den Websites https://webpbn.com , http://nonograms.org und in seinem eigenen (ini-basierten) Format lösen
+ löst Schwarzweiß- und Farb-Nonogramme mit einer beliebigen Anzahl von Farben (die maximale Anzahl von Farben, die erfüllt wurden, beträgt 10).
+ löst Rätsel mit fehlenden Blockgrößen (getupft). Ein Beispiel für ein solches Rätsel .
+ kann Rätsel zur Konsole / zu den Flüchen / zum Fenster im Browser rendern (bei der Installation der zusätzlichen Pynogram-Web- Option). In allen Modi wird die Anzeige des Fortschritts der Lösung in Echtzeit unterstützt.
- langsame Berechnungen (im Vergleich zu den im Artikelvergleich der Löser beschriebenen Implementierungen siehe Tabelle ).
- Ineffizientes Backtracking: Einige Rätsel können stundenlang gelöst werden (wenn der Entscheidungsbaum sehr groß ist).
Rost
Anfang des Jahres begann ich Rust zu studieren. Ich begann wie üblich mit The Book , lernte WASM kennen und ging das vorgeschlagene Tutorial durch . Ich wollte jedoch eine echte Aufgabe, bei der Sie sich auf die Stärken der Sprache einlassen können (vor allem ihre Superleistung), und nicht einige Beispiele, die von jemandem erfunden wurden. Also kehrte ich zu den Nonogrammen zurück. Aber jetzt hatte ich bereits eine funktionierende Version aller Algorithmen in Python, die "nur" neu geschrieben werden musste.
Die gute Nachricht erwartete mich von Anfang an: Es stellte sich heraus, dass Rust mit seinem Typsystem die Datenstrukturen für meine Aufgabe perfekt beschreibt. Mit einer der grundlegenden Entsprechungen von BinaryColor + BinaryBlock / MultiColor + ColouredBlock können Sie beispielsweise Schwarzweiß- und Farb-Nonogramme dauerhaft trennen. Wenn wir irgendwo im Code versuchen, eine farbige Zeichenfolge mit gewöhnlichen binären Beschreibungsblöcken zu lösen, wird ein Kompilierungsfehler bezüglich der Nichtübereinstimmung des Typs angezeigt.
Grundtypen sehen ungefähr so aus pub trait Color { fn blank() -> Self; fn is_solved(&self) -> bool; fn solution_rate(&self) -> f64; fn is_updated_with(&self, new: &Self) -> Result<bool, String>; fn variants(&self) -> Vec<Self>; fn as_color_id(&self) -> Option<ColorId>; fn from_color_ids(ids: &[ColorId]) -> Self; } pub trait Block { type Color: Color; fn from_str_and_color(s: &str, color: Option<ColorId>) -> Self { let size = s.parse::<usize>().expect("Non-integer block size given"); Self::from_size_and_color(size, color) } fn from_size_and_color(size: usize, color: Option<ColorId>) -> Self; fn size(&self) -> usize; fn color(&self) -> Self::Color; } #[derive(Debug, PartialEq, Eq, Hash, Clone)] pub struct Description<T: Block> where T: Block, { pub vec: Vec<T>, }
Bei der Portierung des Codes zeigten einige Punkte deutlich, dass eine statisch typisierte Sprache wie Rust (gut oder beispielsweise C ++) für diese Aufgabe besser geeignet ist. Genauer gesagt beschreiben Generika und Merkmale eine Domäne besser als Klassenhierarchien. Im Python-Code hatte ich zwei Klassen für einen linearen BguSolver , BguSolver und BguColoredSolver die eine Schwarzweiß- bzw. eine Farblinie lösten. Im Rust-Code habe ich immer noch die einzige generische struct DynamicSolver<B: Block, S = <B as Block>::Color> , die beide Arten von Aufgaben lösen kann, abhängig vom Typ, der während der Erstellung übergeben wurde ( DynamicSolver<BinaryBlock>, DynamicSolver<ColoredBlock> ). Dies bedeutet natürlich nicht, dass etwas Ähnliches in Python nicht möglich ist, nur in Rust hat mir das Typsystem klar gezeigt, dass Sie eine Menge sich wiederholenden Codes schreiben müssten, wenn Sie diesen Weg nicht gehen würden.
Darüber hinaus bemerkte jeder, der versuchte, in Rust zu schreiben, zweifellos den Effekt des "Vertrauens" in den Compiler, wenn der Prozess des Schreibens von Code auf den folgenden Pseudo-Meta-Algorithmus hinausläuft:
write_initial_code
while (compiler_hints = $ (Frachtprüfung))! = 0; tun
fix_errors (compiler_hints)
Ende
Wenn der Compiler keine Fehler und Warnungen mehr ausgibt, stimmt Ihr Code mit dem Typsystem und dem Ausleihprüfer überein und Sie warnen vor dem Auftreten einer Reihe potenzieller Fehler (natürlich vorbehaltlich einer sorgfältigen Gestaltung der Datentypen).
Ich werde einige Beispiele für Funktionen geben, die zeigen, wie präzise Rust-Code sein kann (im Vergleich zu Python-Gegenstücken).
ungelöste NachbarnGibt eine Liste ungelöster "Nachbarn" für einen bestimmten Punkt an (x, y)
def unsolved_neighbours(self, position): for pos in self.neighbours(position): if not self.is_cell_solved(*pos): yield pos
fn unsolved_neighbours(&self, point: &Point) -> impl Iterator<Item = Point> + '_ { self.neighbours(&point) .into_iter() .filter(move |n| !self.cell(n).is_solved()) }
TeilsummenGeben Sie für eine Reihe von Blöcken, die eine Zeile beschreiben, Teilsummen an (unter Berücksichtigung der erforderlichen Lücken zwischen den Blöcken). Die resultierenden Indizes geben die Mindestposition an, an der der Block enden kann (diese Informationen werden später für einen linearen Löser verwendet).
Zum Beispiel haben wir für einen solchen Satz von Blöcken [2, 3, 1] am Ausgang [2, 6, 8] , was bedeutet, dass der erste Block maximal nach links verschoben werden kann, so dass sein rechter Rand die zweite Zelle einnimmt, ähnlich wie für den Rest Blöcke:
1 2 3 4 5 6 7 8 9
_ _ _ _ _ _ _ _ _ _
2 3 1 | _ | _ | _ | _ | _ | _ | _ | _ | _ |
^^^
| | |
Ende von 1 Block | | |
Ende von Block 2 -------- |
Ende von Block 3 ------------
@expand_generator def partial_sums(blocks): if not blocks: return sum_so_far = blocks[0] yield sum_so_far for block in blocks[1:]: sum_so_far += block + 1 yield sum_so_far
fn partial_sums(desc: &[Self]) -> Vec<usize> { desc.iter() .scan(None, |prev, block| { let current = if let Some(ref prev_size) = prev { prev_size + block.0 + 1 } else { block.0 }; *prev = Some(current); *prev }) .collect() }
Beim Portieren habe ich einige Änderungen vorgenommen
Nützliche Werkzeuge
- clippy ist ein standardmäßiger statischer Analysator, der manchmal sogar Tipps geben kann, die die Codeleistung leicht steigern.
- valgrind ist ein Tool zur dynamischen Anwendungsanalyse. Ich habe es als Profiler verwendet, um nach Botneks (
valrgind --tool=callgrind ) und besonders nach speicherhungrigen Codeabschnitten ( valrgind --tool=massif ) zu valrgind --tool=massif . Tipp: Setzen Sie [profile.release] debug = true auf Cargo.toml, bevor Sie den Profiler starten. Dadurch bleiben Debug-Zeichen in der ausführbaren Datei. - kcachegrind zum Anzeigen von Callgrind-Dateien. Ein sehr nützliches Werkzeug, um die problematischsten Stellen in Bezug auf die Leistung zu finden.
Leistung
Das für das, was auf Rust umgeschrieben wurde, wurde begonnen. Wir nehmen die Kreuzworträtsel aus der bereits erwähnten Vergleichstabelle und führen sie durch die besten im Originalartikel beschriebenen Löser. Ergebnisse und Beschreibung der Läufe hier . Wir nehmen die resultierende Datei und erstellen ein paar Diagramme darauf. Da die Lösungszeit von Millisekunden bis zu zehn Minuten variiert, wird das Diagramm mit einer logarithmischen Skala erstellt.
laufen in jupyter Laptop import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline
Python-Löser
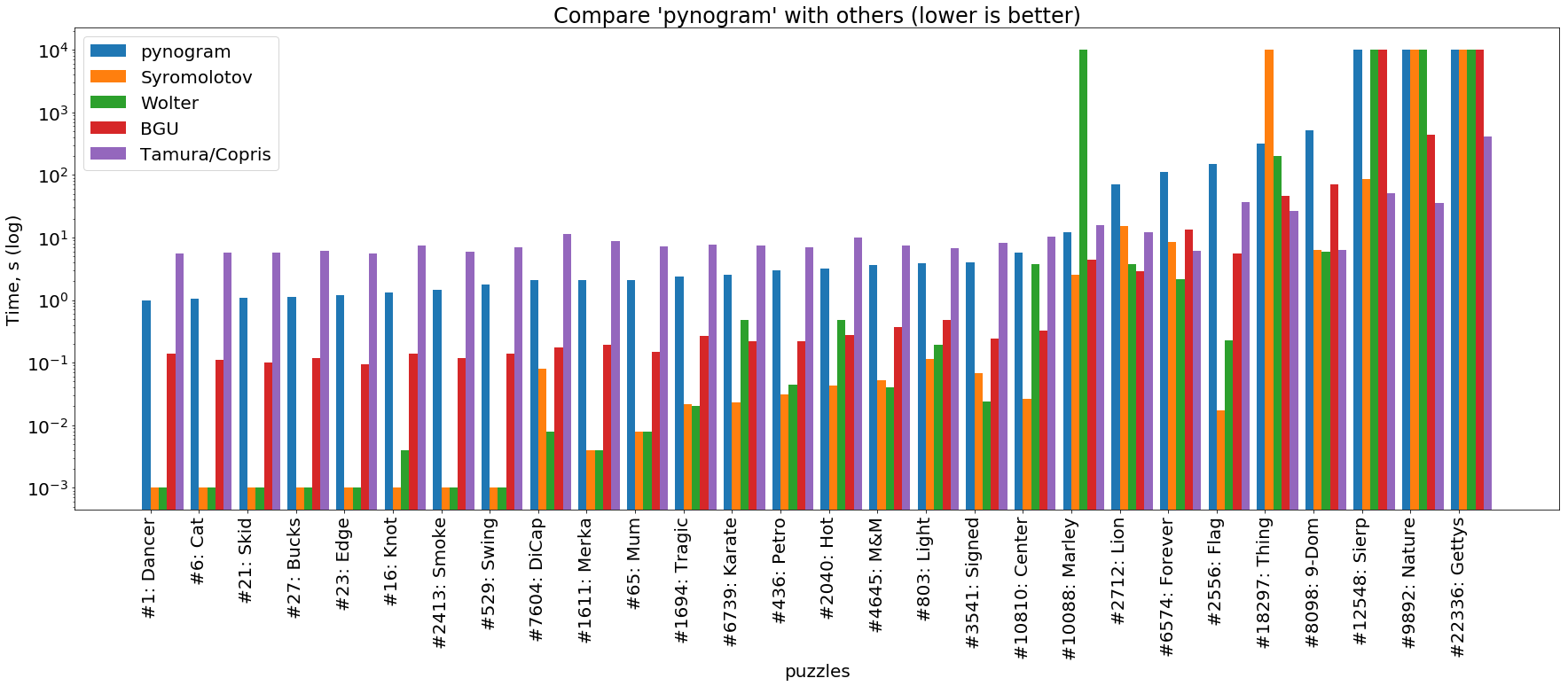
(das Bild ist anklickbar )
Wir sehen, dass das Pynogramm hier langsamer ist als alle vorgestellten Löser. Die einzige Ausnahme von dieser Regel ist der auf SAT basierende Tamura / Copris- Löser, der die einfachsten Rätsel (der linke Teil des Diagramms) länger löst als unsere. Dies ist jedoch ein Merkmal von SAT-Solvern: Sie sind für superkomplexe Kreuzworträtsel konzipiert, bei denen ein regulärer Solver lange Zeit im Backtracking stecken bleibt. Dies ist auf der rechten Seite des Diagramms deutlich sichtbar, wo Tamura / Copris die schwierigsten Rätsel zehn- und hunderte Male schneller löst als alle anderen.
Rostlöser
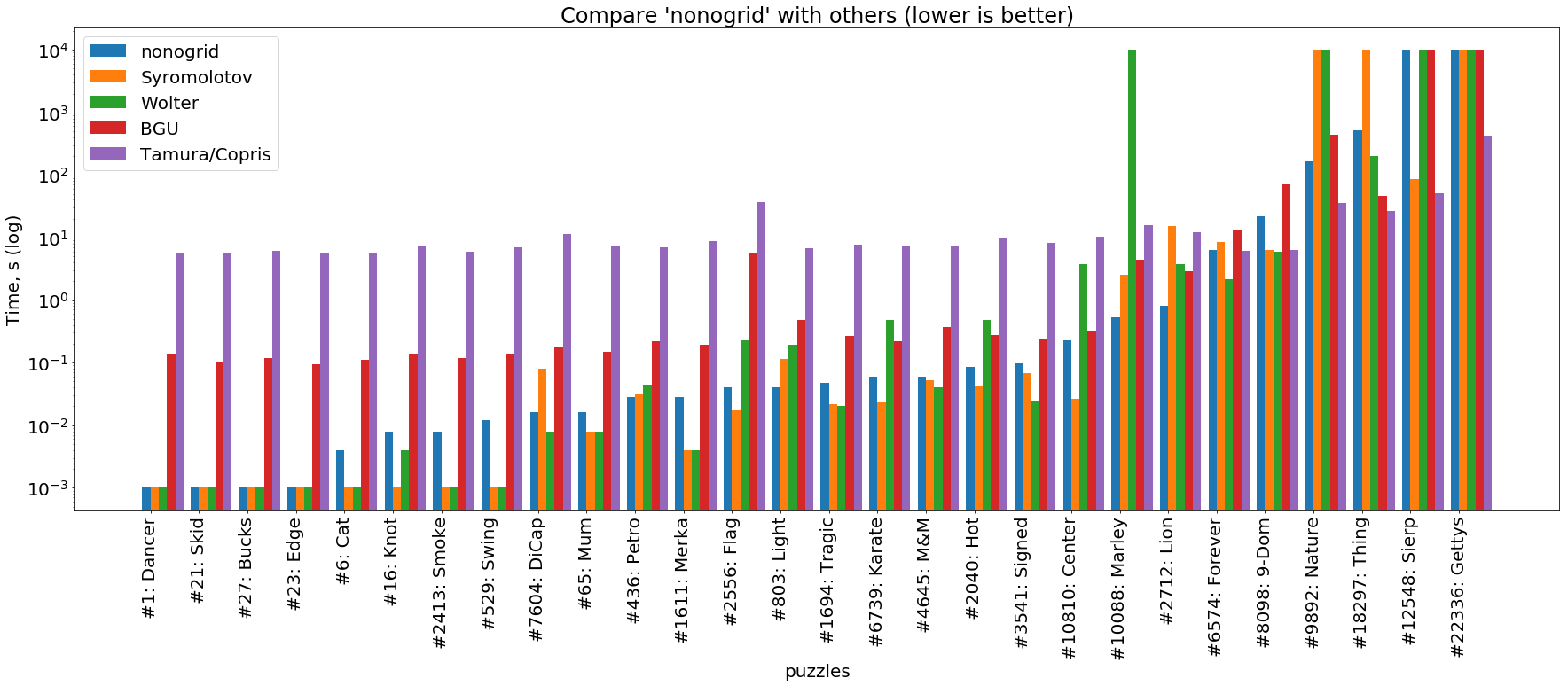
(das Bild ist anklickbar )
Diese Grafik zeigt, dass Nonogrid bei einfachen Aufgaben auch mit Hochleistungslösern in C und C ++ ( Wolter und Syromolotov ) zurechtkommt oder etwas schlechter ist als diese . Mit der Komplikation von Aufgaben wiederholt unser Löser ungefähr die Flugbahn des BGU- Lösers (Java), aber fast immer um eine Größenordnung voraus. Bei den schwierigsten Aufgaben ist Tamura / Copris immer allen voraus.
Rost gegen Python
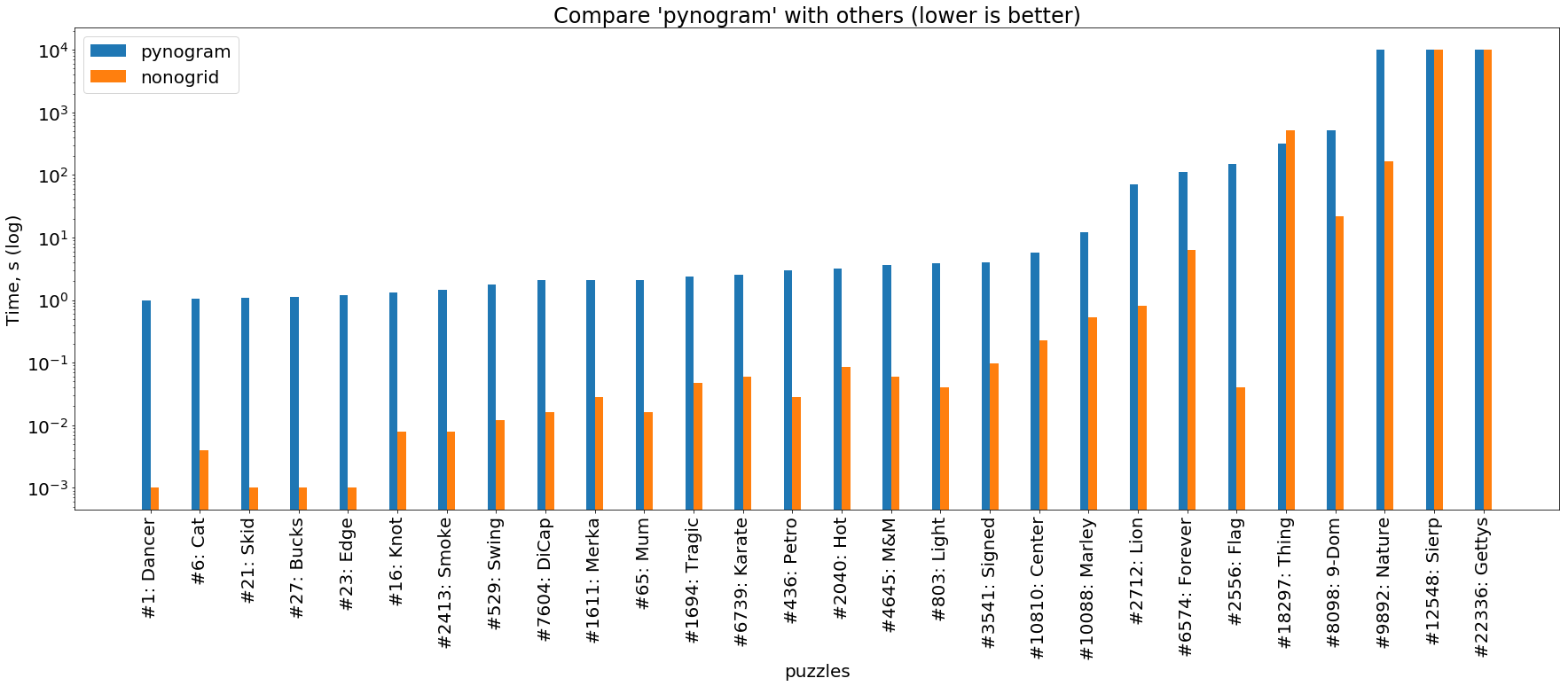
(das Bild ist anklickbar )
Und schließlich ein Vergleich unserer beiden hier beschriebenen Löser. Es ist ersichtlich, dass der Rostlöser fast immer 1-3 Größenordnungen vor dem Pythonlöser liegt.
+ Solver kann alle Rätsel auf den Websites https://webpbn.com (außer geblottet - mit teilweise ausgeblendeten Blockgrößen), http://nonograms.org und seinem eigenen (TOML-basierten) Format lösen
+ löst Schwarzweiß- und Farb-Nonogramme mit einer beliebigen Anzahl von Farben
+ kann Rätsel auf der Konsole rendern (Farbe c webpbn.com zeichnet echte Farbe)
+ arbeitet schnell (im Vergleich zu den im Artikelvergleich der Löser beschriebenen Implementierungen siehe Tabelle).
- Das Backtracking ist wie in der Python-Lösung ineffektiv geblieben: Einige Rätsel (z. B. ein harmloses 20x20 ) können stundenlang gelöst werden (wenn der Entscheidungsbaum sehr groß ist). Vielleicht lohnt es sich, anstelle des Zurückverfolgens die bereits auf dem Hub erwähnten SAT-Löser zu verwenden Der einzige SAT-Löser, den ich auf den ersten Blick bei Rust gefunden habe, scheint zwar unvollendet und verlassen zu sein.
Webassembly
Das Umschreiben des Codes in Rust hat sich also ausgezahlt: Der Solver ist viel schneller geworden. Rust bietet uns jedoch eine weitere unglaublich coole Funktion: die Kompilierung in WebAssembly und die Möglichkeit, Ihren Code direkt im Browser auszuführen.
Um diese Funktion zu implementieren, gibt es ein spezielles Tool für Rust, das die erforderlichen Bindemittel bereitstellt und eine Boilerplate generiert, mit der Sie Rust-Funktionen in JS-Code problemlos ausführen können - dieses Wasm-Pack (+ wasm-bindgen ). Der größte Teil der Arbeit damit und mit anderen wichtigen Tools ist bereits im Tutorial zu Rust und WebAssembly beschrieben . Es gibt jedoch einige Punkte, die ich selbst herausfinden musste:
Beim Lesen entsteht das Gefühl, dass das Tutorial hauptsächlich für einen JS-Entwickler geschrieben wurde, der seinen Code mit Rust beschleunigen möchte. Na ja, oder zumindest für jemanden, der mit npm vertraut ist. Für mich als Person, die weit vom Frontend entfernt ist, war es überraschend, dass selbst das Standardbeispiel aus dem Buch nicht mit einem Webserver eines Drittanbieters arbeiten möchte, der sich vom npm run start von npm run start .
Glücklicherweise verfügt wasm-pack über einen Modus, mit dem Sie regulären JS-Code generieren können (der kein npm-Modul ist). wasm-pack build --target no-modules --no-typescript gibt nur zwei Dateien in der Ausgabe aus: project-name.wasm - die Binärdatei des Rust-Codes, der in WebAssembly und project-name.js kompiliert wurde . Die letzte Datei kann zu jeder HTML-Seite <script src="project-name.js"></script> hinzugefügt werden und verwendet WASM-Funktionen, ohne sich um npm, Webpack, ES6, Module und andere Freuden des modernen JS-Entwicklers zu kümmern. Der Modus no-modules ist ideal für Nicht-Front-End-Entwickler während der Entwicklung einer WASM-Anwendung sowie für Beispiele und Demos, da keine zusätzliche Front-End-Infrastruktur erforderlich ist.
WebAssembly eignet sich für Aufgaben, die für JavaScript zu schwer sind. Zuallererst sind dies Aufgaben, die viele Berechnungen durchführen. Und wenn ja, kann eine solche Aufgabe auch mit WebAssembly lange ausgeführt werden und damit das asynchrone Prinzip des modernen Web verletzen. Ich spreche von allen möglichen Warnungen: Nicht reagierendes Skript , das ich zufällig beobachtet habe, als mein Solver arbeitete. Um dieses Problem zu lösen, können Sie den Web Worker- Mechanismus verwenden. In diesem Fall kann das Schema für die Arbeit mit "schweren" WASM-Funktionen folgendermaßen aussehen:
- Senden Sie über das Hauptskript für ein Ereignis (z. B. Klicken auf eine Schaltfläche) eine Nachricht an den Worker mit der Aufgabe, eine umfangreiche Funktion zu starten.
- , .
- - ()
WASM- JS, WASM . - ( ), HashMap , . ( JS) , / .
, Mutex , thread-safe. smart- . thread-safe Rc Arc RefCell RwLock . : 30%. --features=threaded thread-safe , WASM-.
6574 8098 ( 10 ):
, - 40..70% , , (32..37%) thread-safe ( cargo build --release --features=threaded ).
Firefox 67.0 Chromium 74.0.
WASM- ( ). https://webpbn.com/ http://www.nonograms.org/
Todo
"" /, / .
, . "" , , . .
( , 3600 ). WASM , ( , (!) , , WASM). , , - , nonogrid .
. : , , WASM . , ( ) , JS , .
JS. backtrace, .
( TOML- )
Zusammenfassung
, (, , etc).
Rust 1-3 PyPy 1.5-2 ( ).
Python Rust , Python (, , comprehensions), Rust-.
Rust WebAssembly . Rust , WASM, ( 1.5 ).
- The 'pbnsolve' Paint-by-Number Puzzle Solver by Jan Wolter and the survey
- The BGU Nonograms Project
- Solving Nonograms by combining relaxations
- An Efficient Approach to Solving Nonograms
- Color and black and white Japanese crosswords on-line
- 'Nonolib' library by Dr. Steven Simpson
- Rust and WebAssembly