Spielen Sie Tetris in AR

Mir kam eine etwas seltsame Idee, dass das Haus eine gute Plattform sein könnte, um Tetris zu spielen. Nicht weit von mir war nur ein Gebäude dafür geeignet. Das Ergebnis ist im Video zu sehen:


Das Projekt wird auf einer relativ niedrigen Ebene ohne Verwendung einer vorgefertigten Lösung durchgeführt.

Quellcode

Meistens verwenden sie zwei Optionen für die Implementierung von Augmented Reality:

• markerlos, d.h. Die Position der Kamera wird durch die Bewegung der Schlüsselpunkte ihres Videostreams bestimmt.
• Bild als Markierung relativ zu der Position der Kamera.

Diese Implementierungen erfordern keine besonderen Vorbereitungen oder besonderen Bedingungen.

Es gibt eine weitere Implementierungsoption: Sie können ein bestimmtes Objekt erkennen und als Marker verwenden. Dies erfordert zumindest seine Anwesenheit, ermöglicht jedoch eine visuelle Steuerung. Eine der Methoden einer solchen Erkennung ist die Erkennung eines Objekts durch Kanten. Es hat Einschränkungen - das Markierungsobjekt muss klar definierte Kanten haben, d.h. Das Objekt sollte höchstwahrscheinlich fest sein.

Oder die Kanten sollten klar abgegrenzt sein, wie zum Beispiel die Beleuchtung dieses Gebäudes:



Es ist ersichtlich, dass die Hintergrundbeleuchtung im Bild leicht getrennt und zur Erkennung verwendet werden kann.

Implementierung

Auf Qt. Mit diesem Framework können Sie auf verschiedenen Plattformen und gleichzeitig in C ++ arbeiten. Da Leistung für uns wichtig ist, scheinen die Profis eine naheliegende Wahl zu sein.

Obwohl Qt mit Android nicht sehr gut funktionierte (langer Start, Debugging war deaktiviert), wurde dies alles durch die Möglichkeit ausgeglichen, den Algorithmus auf dem Desktop zu debuggen.

Dreidimensionale Grafiken wurden auf der in Qt eingebetteten OpenGL-Rohdaten visualisiert.

Die Arbeit mit der Kamera wurde über Qt durchgeführt. Zum Debuggen wurde ein Video aufgenommen, und es war praktisch genug, den Videostream der Kamera durch einen Videostream aus einer Datei zu ersetzen.

Die Ausgabe erfolgte über qml-Tools. Freunde zu finden qml und OpenGL war nicht ohne Probleme, aber wir werden nicht weiter darauf eingehen.

Zur Bildverarbeitung ist die OpenCV-Bibliothek angeschlossen.

Tracking-Algorithmus

Kommen wir nun zum interessantesten Teil - dem Algorithmus zum Verfolgen eines Objekts entlang seiner Kanten.
Beginnen Sie mit dem Hervorheben der Kanten im Bild. In unserem Fall haben alle Kanten die Form von geraden Linien. Der erste Gedanke, der mir einfällt, ist die Verwendung eines Liniendetektors. Hough-Transformationen könnten als Zeilendetektor verwendet werden. Dieser Weg scheint mir jedoch nicht sehr wahr zu sein, da die Hough-Transformation ziemlich teuer ist und dieser Detektor nicht sehr zuverlässig ist (dies ist subjektiv, vielleicht hängt alles von der Aufgabe ab).
Gehen wir stattdessen anders und allgemeiner vor. Wir werden nicht berücksichtigen, dass unsere Linien gerade sind, aber wir werden einfach an einem Binärbild arbeiten. Das Vorhandensein von Kanten wird in das Binärbild codiert. Das heißt, Ein Pixel mit dem Wert Null bedeutet, dass sich an dieser Stelle eine Kante befindet. Der Pixelwert ist größer als Null. Es gibt keine Kante. Ein solches Bild kann unter Verwendung eines Canny-Grenzdetektors oder unter Verwendung einer einfachen Schwellwerttransformation erhalten werden . Diese Algorithmen finden Sie in OpenCV.

OpenCV hat jetzt auch eine andere nützliche Funktion für uns - distanceTransform , die ein Binärbild am Eingang und ein Bild am Ausgang liefert, in Pixeln, deren Abstand zum nächsten Nullpixel codiert ist.

Nehmen wir nun an, wir haben bereits die erste gute Annäherung, wo sich unser Modell befinden sollte. Als nächstes beschreiben wir die Fehlerfunktion, die beschreibt, inwieweit die Kanten unserer Näherung nicht mit den Kanten im resultierenden Bild übereinstimmen. Mit dem Bild von distanceTransform können wir dies bereits tun. Und dann führen wir den Funktionsoptimierungsalgorithmus aus und ändern nur unsere Annäherung an die Position des Objekts im Raum. Infolgedessen sollte unsere Annäherung die tatsächliche Position des Objekts ziemlich genau beschreiben.
Infolgedessen kann der Algorithmus in zwei Stufen unterteilt werden:

1. Bildvorverarbeitung - Binärisierung, Filterung und Verwendung der Funktion distanceTransfrom.
2. Tracking - Optimierung der Fehlerfunktion.

Bildvorverarbeitung

An dieser Stelle müssen Sie die Kanten im Bild hervorheben. Sie können den Canny-Grenzdetektor verwenden, aber in unserem Fall funktioniert die übliche Schwellenwertkonvertierung oder ihre adaptive Version besser (in OpenCV sind dies Schwellenwert- oder adaptive Schwellenwertfunktionen). Es ist klar, dass ein solches Bild Rauschen aufweist, daher ist eine Filterung erforderlich. Gehen wir wie folgt vor: Wählen Sie die Kontur mit der OpenCV-Funktion findCountours aus und löschen Sie Segmente, die zu klein oder zu wenig wie eine Linie sind.

Das Verarbeitungsergebnis ist im Bild zu sehen:



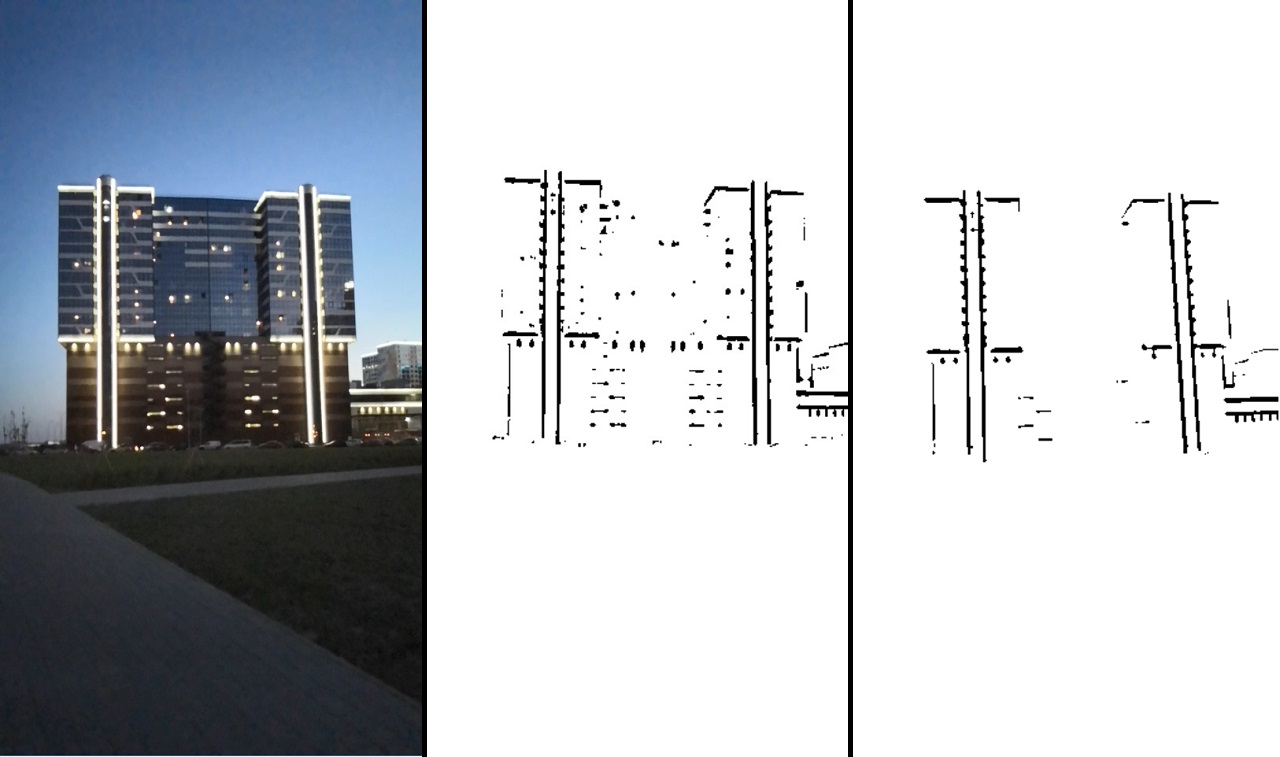
Konsistent: das Originalbild -> nach der Schwellenwerttransformation -> nach dem Filtern.

Dieses Bild zeigt uns schon ganz deutlich, wo sich der rechte Rand befindet und wo nicht. Danach verwenden wir die Funktion distanceTransform. Als Ergebnis erhalten wir Informationen darüber, wie weit jeder Punkt von der Kante entfernt ist. Das resultierende Bild wird als bezeichnet .

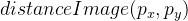
So sieht es aus, wenn es normalisiert und visualisiert wird:



Als nächstes benötigen wir einige mathematische Werkzeuge.

Funktionsoptimierungsalgorithmus

Funktionsoptimierung ist die Aufgabe, das Minimum einer Funktion zu finden.

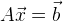
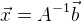
Wenn es sich um ein lineares Gleichungssystem handelt, ist es recht einfach, ein Minimum zu finden. Stellen Sie sich das Gleichungssystem in Matrixform vor: , dann unsere Lösung: . Wenn wir ein überbestimmtes Gleichungssystem haben, können wir die Methode der kleinsten Quadrate verwenden : .

Wenn unsere Funktion nicht linear ist, wird die Aufgabe komplizierter. Um das Minimum zu finden, können Sie den Gauß-Newton-Algorithmus verwenden . Der Algorithmus funktioniert wie folgt:

1. Es wird davon ausgegangen, dass wir bereits eine erste Annäherung an die Lösung haben was wir iterativ verfeinern werden.
2. Mit der Taylor-Erweiterung können wir unsere nichtlineare Funktion am aktuellen Approximationspunkt linear approximieren. Wir lösen das resultierende lineare Gleichungssystem nach der Methode der kleinsten Quadrate 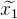. Infolgedessen ist die resultierende Lösung keine Lösung, sondern näher als die aktuelle Näherung.
3. Ersetzen Sie die aktuelle Näherung Entscheidung erhalten 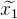und fahren Sie mit Schritt 2 fort. Wiederholen Sie diesen Vorgang, bis der Unterschied zwischen und wird nicht kleiner als ein bestimmter Wert sein.

Lassen Sie uns den Algorithmus genauer analysieren.

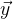
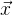
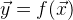
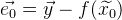
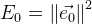
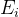
Lass - Arbeitsfunktion, - ein zuvor bekannter Vektor von Funktionswerten. Mit der perfekten Lösung der Gleichung Die folgende Aussage ist wahr . Wir haben aber nur eine Annäherung . Dann wird der Fehlervektor aus dieser Näherung bezeichnet als: . Ein allgemeiner Fehler der Funktion ist: . Jetzt solche finden bei denen Wenn wir ein Minimum erreichen, erhalten wir eine bessere Annäherung an die Lösung .
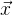
Ausgehend von der Annäherung Wir werden es iterativ approximieren und bei jeder Iteration ankommen . Dazu benötigen wir jede Iteration, um die Jacobi-Matrix für die Funktion zu berechnen für die aktuelle Näherung, bestehend aus Ableitungen unserer Funktion:

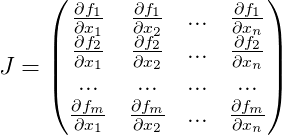
Und die folgende Annäherung wird gegeben als: .
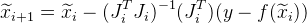
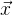
Oft sind Aufgaben so aufgebaut, dass wir eine große Anzahl von Daten unabhängig voneinander haben (nur von den Werten ) Infolgedessen ist die allgemeine Jacobi-Matrix sehr spärlich. Es gibt eine Möglichkeit, die Berechnungen zu optimieren.
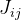
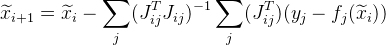
Angenommen, eine gemeinsame Funktion wird aus einer Reihe von Punkten berechnet. Ab dem j-ten Punkt bekommen wir . Anstatt die Jacobi-Matrix zu berechnen Für die gesamte Funktion berechnen wir die Jacobi-Matrix speziell für und bezeichnen es als: . Dann wird die folgende Annäherung wie folgt angegeben: . Darüber hinaus können Sie mit dieser Änderung die Berechnungen parallelisieren.
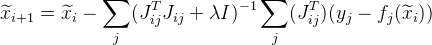
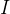
Es kann vorkommen, dass der folgende Wert wird einen größeren Fehler geben als . Um dieses Problem zu lösen, können Sie eine Modifikation des Algorithmus verwenden - den Levenberg-Marquardt-Algorithmus . Mehrwert schaffen in unsere Formel: wo Ist eine Einheitsmatrix. Wert wie folgt ausgewählt:

• Erstens hat es einen eher kleinen Wert (so dass der Algorithmus konvergiert).
• dann wenn ein Fehler für mehr als , dann erhöhen Sie den Wert und versuchen Sie, den Fehler für zu berechnen wieder.

Je nichtlinearer die Funktion Je größer der Wert sein sollte . Je größer jedoch der Wert Je langsamer der Algorithmus konvergiert.

Wir vervollständigen den Algorithmus, wenn anders als klein genug und nehmen als Lösung.

Der Algorithmus ist ziemlich universell und kann für eine Vielzahl von Aufgaben verwendet werden.

Mathematisches Verfolgungsmodell

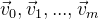
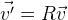
Da es sich um Koordinaten im Raum handelt, ist es klar, dass wir diese Koordinaten manipulieren können müssen. Angenommen, wir haben einige Punkte . Und wir müssen sie mit Nullkoordinaten um den Punkt drehen. Der wahrscheinlich einfachste Weg wäre die Verwendung der Rotationsmatrix R , die die erforderliche Rotation beschreibt: . Wenn wir die Punkte verschieben müssen, fügen Sie einfach den gewünschten Vektor t hinzu : .
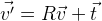
So können Sie die Position eines Objekts im Raum beliebig ändern. Es stellt sich heraus, dass die Koordinaten des Objekts durch die dreidimensionale Matrix R und den dreidimensionalen Vektor t bestimmt werden , d.h. 12 Parameter. Darüber hinaus sind diese Parameter nicht unabhängig voneinander, die Komponenten der Rotationsmatrix sind durch bestimmte Bedingungen miteinander verbunden. Unter dem Gesichtspunkt der Verwendung dieser Funktionen bei der Optimierung sind diese Parameter daher nicht die beste Lösung. Es gibt mehr Parameter als Freiheitsgrade, es gibt eine Beziehung zwischen ihnen. Es gibt eine andere Form der Rotation - Rodrigues Rotationsformel . Diese Drehung wird durch drei Parameter spezifiziert, die einen dreidimensionalen Vektor bilden.

Der normalisierte Vektor ist die Rotationsachse, und die Länge dieses Vektors ist der Rotationswinkel um diese Achse.

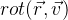
Wir setzen die Rotationsfunktion des Vektors v : unter Verwendung der r- Parameter der Rodrigue-Formel. Daraus ergibt sich folgende Formel: .
Und am Ende können wir die Koordinaten der Position des Objekts mit einem 6-dimensionalen Vektor festlegen:
Wir erhalten die folgende Formel: .

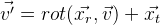
Lochkameramodell

Nun beschreiben wir ein einfaches mathematisches Modell der im Projekt verwendeten Kamera:

$$

$$\ vec {p} = \ begin {pmatrix} p_x & p_y \ end {pmatrix} ^ T = cam (\ vec {v}) = \ begin {pmatrix} f_x \ frac {v_x} {v_z} + c_x & f_y \ frac {v_y} {v_z} + c_y \ end {pmatrix} ^ T$$

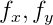
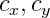
wo - Brennweite in Pixel; - Das optische Zentrum ist ebenfalls in Pixel angegeben. Dies sind einzelne Kameraparameter, die als intrinsische Parameter der Kamera bezeichnet werden. Typischerweise sind diese Parameter im Voraus bekannt. In diesem Projekt werden diese Parameter per Auge ausgewählt.

Dieses Modell berücksichtigt nicht die Objektivverzerrung der Kameras ( Verzerrung ). Angenommen, sie sind es nicht.

Mit diesem Modell erhalten wir eine zentrale Projektion, deren Punkte umso mehr zum optischen Zentrum tendieren, je weiter sie von der Kamera entfernt sind. So erhalten wir die Wirkung einer sich verengenden Eisenbahn:



Im Raum ist die Kamera mit der z- Achse ausgerichtet, die Bildebene ist parallel zur xy- Ebene. Wir ergänzen unser Modell mit der Fähigkeit, sich im Raum zu bewegen:

$$

$$\ vec {p} _j = cam (rot (\ vec {x} _r, \ vec {v} _j) + \ vec {x} _t)$$

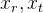
So haben wir ein Modell erhalten, mit dem wir in algebraischer Form die Projektion von Punkten von der Außenwelt auf das Kamerabild (von den Weltkoordinaten zum Bildschirm) simulieren können. Für uns sind die Parameter der relativen Position der Kamera im Raum in diesem Modell unbekannt. . Diese Parameter werden als extrinsische Parameter der Kamera bezeichnet.

Tracking

Bereits ohne OpenCV-Tools implementiert. Zunächst müssen wir die Fehlerfunktion für unsere oben beschriebene Näherungslösung erhalten. Und wir werden die Berechnung schrittweise schreiben:

1. Wir wählen solche Kanten des Verfolgungsmodells aus, die basierend auf den Parametern der aktuellen Näherung sichtbar sind.
2. Wir verwandeln den ausgewählten Satz von Kanten in einen festen Satz von Punkten, um die Berechnungen zu vereinfachen. Es ist beispielsweise möglich, die n-te Anzahl von Punkten von jeder Kante zu nehmen oder (eine korrektere Option) eine solche Menge so zu wählen, dass zwischen den Punkten ein fester Abstand in Pixel besteht. Wir werden sie Kontrollpunkte nennen (im Projekt: controlPoint - Kontrollpunkte und controlPixelDistance - der gleiche feste Abstand in Pixel).
3. Wir projizieren Kontrollpunkte auf das Bild. Dank distanceImage können wir den Abstand der Projektion des Kontrollpunkts zum Rand im Bild ermitteln. Im Idealfall sollten alle Kontrollpunkte streng an den Bildrändern liegen, d.h. Der Abstand zur Rippe sollte Null sein. Basierend darauf erhalten wir einen Fehler für einen bestimmten Kontrollpunkt: .
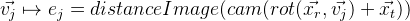4. Wir erhalten folgende Fehlerfunktion:

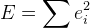
Jetzt bleibt ein Minimum von E. zu finden . Dazu verwenden wir den oben beschriebenen Levenberg-Marquardt-Algorithmus. Wie wir bereits wissen, erfordert der Algorithmus die Berechnung der Jacobi-Matrix, d.h. abgeleitete Funktionen. Sie können die numerische Ermittlung von Derivaten verwenden. Sie können auch einige vorgefertigte Lösungen für diesen Algorithmus verwenden. In diesem Projekt wurde jedoch alles manuell geschrieben, sodass ich den vollständigen Abschluss der gesamten Lösung beschreiben werde.

Für jeden Kontrollpunkt erhalten wir eine von anderen Punkten unabhängige Gleichung. Es wurde bereits oben beschrieben, dass es in diesem Fall möglich ist, diese Gleichungen unabhängig voneinander zu betrachten und die Jacobi-Matrix spezifisch für jede zu berechnen. Wir werden es der Reihe nach anhand der Differenzierungsregeln einer komplexen Funktion analysieren:



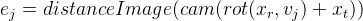
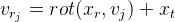
Wir bezeichnen dann



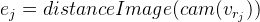
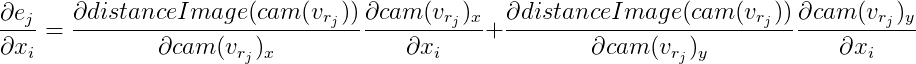
Von hier aus:



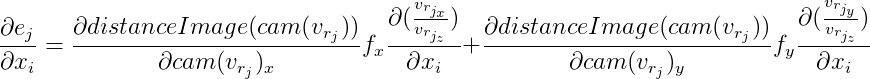
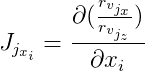
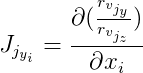
Weiter bezeichnen wir und dann:


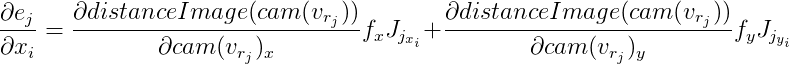
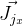
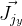
Die Ableitungen von distanceImage sind numerisch. Und zur Berechnung von Vektoren und Sie müssen Derivate gemäß der Rotationsformel von Rodrigue finden. Ich fand Jacobian durch diese Formel in der Veröffentlichung „Eine kompakte Formel für die Ableitung einer 3-D-Rotation in
Exponentialkoordinaten »Guillermo Gallego, Anthony Yezzi :

,
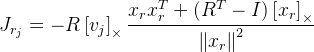
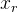
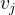
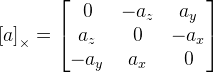
wobei R die Rotationsmatrix ist, die durch die Rodrigue-Formel aus dem Rotationsvektor erhalten wird ;; - der Punkt, den wir drehen; Ich bin die Identitätsmatrix; . Wie wir hier sehen, haben wir eine Division durch die Länge des Rotationsvektors, und wenn der Vektor Null ist, funktioniert die Formel nicht mehr. Dies liegt wahrscheinlich daran, dass beim Nullvektor die Rotationsachse nicht definiert ist. Wenn der Rotationsvektor sehr nahe bei Null liegt, verwenden wir diese Formel: .
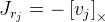
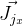
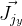
Es bleibt zu malen und (hier wird Index j weggelassen):


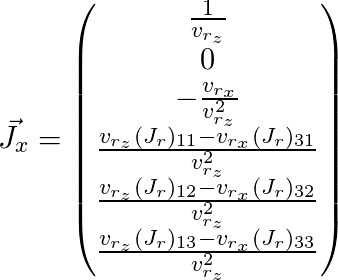
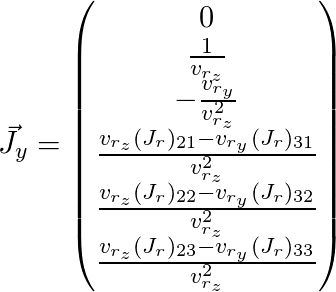
Somit haben wir die Jacobi-Matrix für den Punkt erhalten, den wir benötigen, und können sie für den oben beschriebenen Optimierungsalgorithmus verwenden.

Bei diesem Algorithmus gibt es mehrere Probleme. Erstens Genauigkeit. Infolgedessen springt die globale Position der Kamera leicht von Bild zu Bild. Sie können es ein bisschen beheben. Wir haben a priori Informationen, dass sich die Kameraposition von Bild zu Bild nicht dramatisch ändern kann. Und wir können diesen Jitter reduzieren, indem wir der Funktion zusätzliche Gleichungen hinzufügen.

Es ist zu beachten, dass der Verschiebungsvektor t in unserem Fall nicht die Koordinate der globalen Position der Kamera ist. Die globale Position ist ein lokaler Punkt mit Nullkoordinaten und kann daher wie folgt abgeleitet werden:



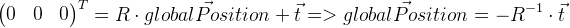
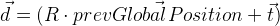
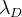
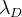
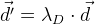
Wir erinnern uns an die Position des vorherigen Frames in prevGlobalPosition . Jetzt sollte die vorherige Position nahe Null sein, d.h. Vektorlänge sollte klein genug sein. Das heißt, Neben anderen Abweichungswerten muss auch der Vektor d minimiert werden. Um den Grad des Einflusses dieser Modifikation zu bestimmen, führen wir den Wert ein und multipliziere den Vektor d durch Addieren mit :: . Das heißt, im Optimierungsalgorithmus minimieren wir zusätzlich den Vektor d ' . Dazu muss natürlich die Jacobi-Matrix dafür berechnet werden, die auf die gleiche Weise abgeleitet wird, wie wir sie oben bereits für die allgemeine Fehlerfunktion abgeleitet haben.

Das zweite Problem des Algorithmus ist, dass er in lokalen Minima stecken bleiben kann. In anderen Arbeiten wird dieses Problem mit einem Partikelfilter gelöst . In unserem Fall hat sich diese Option im Prinzip als ausreichend erwiesen.

Boni von der Verfolgung eines Objekts

Wenn Sie die Position und Form des Objekts kennen, können Sie sie visuell bearbeiten, was ich im Video zu demonstrieren versucht habe. Das Objekt wurde mit OpenGL-Shadern verzerrt. Mit Hilfe unseres Modells habe ich den Punkt des Objekts auf das Bild projiziert und so die Farbe dieses Punktes erhalten. Dann können Sie diesen Punkt verschieben und interessante Effekte erzielen - zum Beispiel Morphing. Man muss jedoch bedenken, dass es notwendig ist, dass etwas an seinem Platz bleibt, wenn man den Punkt verschiebt, sonst werden Inkonsistenzen spürbar. Abhängig von der Qualität unserer Verfolgung und der Form des Objekts erhalten wir außerdem verschiedene unerwünschte Effekte aufgrund von akkumulierten Fehlern, die immer noch auftreten. Es muss nur irgendwie berücksichtigt werden. In dem oben gezeigten Video wollte ich zeigen, dass Augmented Reality etwas weiter verwendet werden kann, als nur virtuelle Objekte auf das Bild zu setzen.

Übrigens implementiert das Vuforia SDK die Verfolgung eines Objekts anhand seiner Form, obwohl ich nicht denke, dass es möglich wäre, dieses Projekt damit zu implementieren, da es nicht möglich ist, streng definierte Kanten zu verwenden und nicht mit der Beleuchtung des Gebäudes verbunden werden kann.