In einem Artikel des Stitch Fix-Teams wird vorgeschlagen, bei Marketing- und Produkt-A / B-Tests einen klinischen Forschungsansatz für Nicht-Minderwertigkeitsstudien zu verwenden. Dieser Ansatz ist wirklich anwendbar, wenn wir eine neue Lösung testen, die Vorteile bietet, die durch Tests nicht messbar sind.
Das einfachste Beispiel ist der Knochenverlust. Zum Beispiel automatisieren wir den Prozess der Zuweisung der ersten Lektion, möchten aber die Durchgangskonvertierung nicht viel fallen lassen. Oder wir testen Änderungen, die sich auf ein Benutzersegment konzentrieren, und stellen gleichzeitig sicher, dass die Conversions in anderen Segmenten nicht stark sinken (vergessen Sie beim Testen mehrerer Hypothesen nicht die Korrekturen).
Die Wahl des rechten Randes mit nicht geringerer Effizienz führt zu zusätzlichen Schwierigkeiten in der Testentwurfsphase. Die Frage, wie Δ in dem Artikel zu wählen ist, ist nicht gut offenbart. Es scheint, dass diese Wahl in klinischen Studien nicht vollständig transparent ist.
Eine Überprüfung der medizinischen Veröffentlichungen zu Nicht-Minderwertigkeitsberichten zeigt, dass in nur der Hälfte der Veröffentlichungen die Wahl der Grenze gerechtfertigt ist und diese Begründungen häufig nicht eindeutig oder nicht detailliert sind.
In jedem Fall scheint dieser Ansatz interessant zu sein, weil Durch Reduzieren der erforderlichen Stichprobengröße kann die Testgeschwindigkeit und damit die Entscheidungsgeschwindigkeit erhöht werden. -
Daria Mukhina, Produktanalystin für die mobile Skyeng-App.Das Stitch Fix Team liebt es, verschiedene Dinge zu testen. Grundsätzlich führt die gesamte Technologie-Community gerne Tests durch. Welche Version der Website zieht mehr Benutzer an - A oder B? Bringt Version A des Empfehlungsmodells mehr Geld als Version B? Um Hypothesen zu testen, verwenden wir fast immer den einfachsten Ansatz eines grundlegenden Statistikkurses:
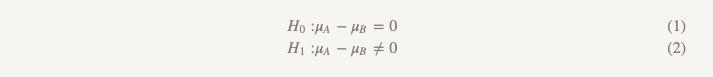
Obwohl wir den Begriff selten verwenden, wird diese Form des Testens als „Hypothese des Überlegenheitstests“ bezeichnet. Bei diesem Ansatz gehen wir davon aus, dass zwischen den beiden Optionen kein Unterschied besteht. Wir halten an dieser Idee fest und lehnen sie nur ab, wenn die erhaltenen Daten dafür überzeugend genug sind - das heißt, sie zeigen, dass eine der Optionen (A oder B) besser ist als die andere.
Das Testen der Überlegenheitshypothese eignet sich zur Lösung vieler Probleme. Wir veröffentlichen die B-Version des Empfehlungsmodells nur, wenn sie offensichtlich besser ist als die bereits verwendete Version A. In einigen Fällen funktioniert dieser Ansatz jedoch nicht so gut. Schauen wir uns einige Beispiele an.
1) Wir verwenden einen Drittanbieter-Service , mit dessen Hilfe gefälschte Bankkarten identifiziert werden können. Wir haben einen anderen Service gefunden, der deutlich weniger kostet. Wenn ein billigerer Service so gut funktioniert wie der, den wir jetzt nutzen, werden wir ihn wählen. Es muss nicht besser sein als der verwendete Dienst.
2) Wir möchten die Datenquelle A verlassen und durch die Datenquelle B ersetzen. Wir könnten das Verlassen von A verzögern, wenn B zu sehr schlechten Ergebnissen führt, aber es ist nicht möglich, A weiter zu verwenden.
3) Wir möchten vom Ansatz zur Modellierung A zum Ansatz B übergehen, nicht weil wir von B bessere Ergebnisse erwarten, sondern weil dies uns eine große betriebliche Flexibilität bietet. Wir haben keinen Grund zu der Annahme, dass B schlechter sein wird, aber wir werden den Übergang nicht beginnen, wenn dies der Fall ist.
4) Wir haben einige qualitative Änderungen am Website-Design (Version B) vorgenommen und sind der Ansicht, dass diese Version Version A überlegen ist. Wir erwarten keine Änderungen bei der Conversion oder bei wichtigen Leistungsindikatoren, anhand derer wir die Website normalerweise bewerten. Wir glauben jedoch, dass Parameter Vorteile haben, die entweder nicht messbar sind oder unsere Technologien nicht ausreichen, um sie zu messen.
In all diesen Fällen ist die Erforschung von Spitzenleistungen nicht die beste Lösung. Die meisten Experten in diesen Situationen verwenden es jedoch standardmäßig. Wir führen sorgfältig ein Experiment durch, um das Ausmaß des Effekts korrekt zu bestimmen. Wenn es stimmt, dass die Versionen A und B sehr ähnlich funktionieren, besteht die Möglichkeit, dass wir die Nullhypothese nicht ablehnen können. Schließen wir daraus, dass A und B im Allgemeinen gleich funktionieren? Nein! Die Unfähigkeit, die Nullhypothese abzulehnen, und die Annahme der Nullhypothese sind nicht dasselbe.
Berechnungen der Stichprobengröße (die Sie natürlich durchgeführt haben) werden normalerweise mit strengeren Grenzen für den Fehler der ersten Art (Wahrscheinlichkeit einer fehlerhaften Ablehnung der Nullhypothese, oft als Alpha bezeichnet) als für den Fehler der zweiten Art (Wahrscheinlichkeit, dass die Nullhypothese nicht abgelehnt wird, durchgeführt, wenn unter der Annahme, dass die Nullhypothese falsch ist (oft Beta genannt). Der typische Wert für Alpha beträgt 0,05, während der typische Wert für Beta 0,20 beträgt, was einer statistischen Potenz von 0,80 entspricht. Dies bedeutet, dass wir mit einer Wahrscheinlichkeit von 20% den tatsächlichen Einfluss des Werts, den wir in unseren Leistungsberechnungen angegeben haben, nicht erkennen können. Dies ist eine ziemlich schwerwiegende Informationslücke. Betrachten wir als Beispiel die folgenden Hypothesen:
H0: Mein Rucksack ist NICHT in meinem Zimmer (3)
H1: Mein Rucksack ist in meinem Zimmer (4)Wenn ich mein Zimmer durchsucht und meinen Rucksack gefunden habe - gut, kann ich die Nullhypothese ablehnen. Aber wenn ich mich im Raum umsah und meinen Rucksack nicht finden konnte (Abbildung 1), welche Schlussfolgerung sollte ich ziehen? Bin ich sicher, dass er nicht da ist? Habe ich gründlich genug gesucht? Was ist, wenn ich nur 80% des Raumes durchsucht habe? Zu dem Schluss zu kommen, dass der Rucksack definitiv nicht im Raum ist, wird eine vorschnelle Entscheidung sein. Es überrascht nicht, dass wir "die Nullhypothese nicht akzeptieren" können.
Das Gebiet, das wir gesucht haben
Wir haben keinen Rucksack gefunden - sollten wir die Nullhypothese akzeptieren?Abbildung 1. Das Durchsuchen von 80% des Raums entspricht in etwa der Durchführung einer Studie mit einer Kapazität von 80%. Wenn Sie keinen Rucksack gefunden haben, nachdem Sie 80% des Zimmers untersucht haben, können Sie daraus schließen, dass er nicht vorhanden ist?Was macht ein Datenspezialist in dieser Situation? Sie können die Forschungsleistung erheblich steigern, benötigen dann jedoch eine viel größere Stichprobe, und das Ergebnis ist immer noch unbefriedigend.
Glücklicherweise sind solche Probleme in der Welt der klinischen Forschung seit langem untersucht worden. Medikament B ist billiger als Medikament A; Medikament B wird voraussichtlich weniger Nebenwirkungen verursachen als Medikament A; Medikament B ist einfacher zu transportieren, da es nicht im Kühlschrank aufbewahrt werden muss und Medikament A benötigt wird. Wir testen die Hypothese einer nicht geringeren Effizienz. Dies ist notwendig, um zu zeigen, dass Version B so gut wie Version A ist - zumindest innerhalb einer bestimmten vorgegebenen Grenze von "nicht weniger Effizienz", Δ. Wenig später werden wir mehr darüber sprechen, wie diese Grenze festgelegt werden kann. Nehmen wir nun an, dass dies der kleinste Unterschied ist, der praktisch signifikant ist (im Zusammenhang mit klinischen Studien wird dies normalerweise als klinische Relevanz bezeichnet).
Hypothesen von nicht geringerer Effizienz stellen alles auf den Kopf:
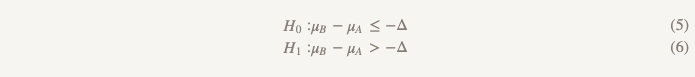
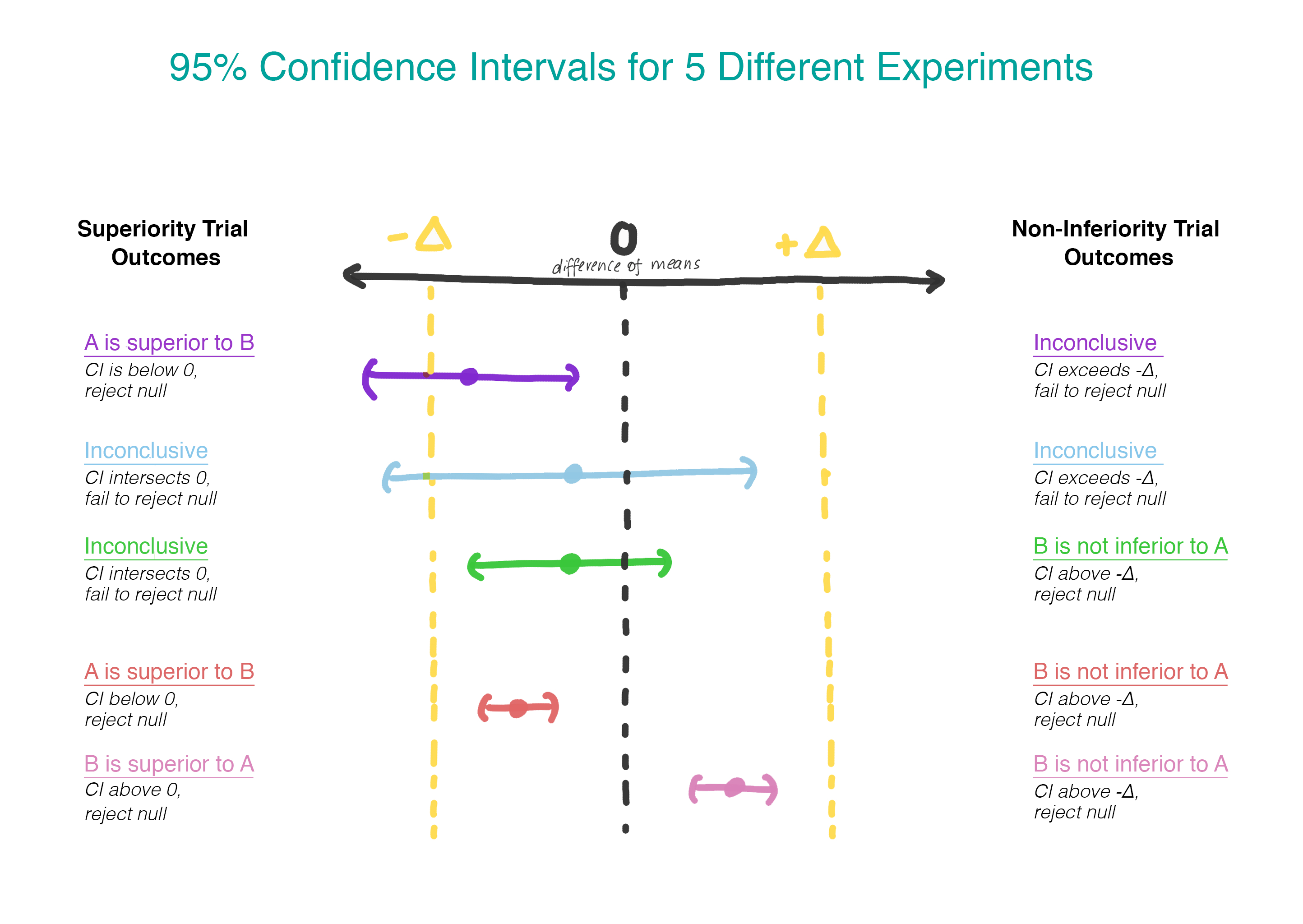
Anstatt davon auszugehen, dass es keinen Unterschied gibt, gehen wir davon aus, dass Version B schlechter als Version A ist, und wir werden an dieser Annahme festhalten, bis wir zeigen, dass dies nicht der Fall ist. Dies ist genau der Moment, in dem es sinnvoll ist, eine einseitige Hypothese zu testen! In der Praxis kann dies erreicht werden, indem ein Konfidenzintervall erstellt und bestimmt wird, ob das Intervall wirklich größer als Δ ist (Abbildung 2).
Δ Auswahl
Wie wähle ich Δ? Der Auswahlprozess Δ umfasst eine statistische Begründung und eine Subjektbewertung. In der Welt der klinischen Studien gibt es normative Empfehlungen, aus denen hervorgeht, dass das Delta der kleinste klinisch signifikante Unterschied sein sollte - einer, der in der Praxis relevant sein wird. Hier ist ein Zitat der europäischen Führung, mit dem Sie sich selbst überprüfen können: „Wenn der Unterschied richtig gewählt wurde, reicht ein Konfidenzintervall, das vollständig zwischen –∆ und 0 ... liegt, immer noch aus, um nicht weniger Effizienz zu demonstrieren. Wenn dieses Ergebnis nicht akzeptabel erscheint, bedeutet dies, dass ∆ nicht angemessen ausgewählt wurde. “
Das Delta sollte das Ausmaß der Wirkung von Version A in Bezug auf die wahre Kontrolle (Placebo / fehlende Behandlung) definitiv nicht überschreiten, da dies uns zu der Annahme führt, dass Version B schlechter als die wahre Kontrolle ist und gleichzeitig „nicht weniger Effizienz“ zeigt. Angenommen, bei der Einführung von Version A war Version 0 an ihrer Stelle oder die Funktion war überhaupt nicht vorhanden (siehe Abbildung 3).
Basierend auf den Ergebnissen des Testens der Überlegenheitshypothese wurde das Ausmaß des Effekts E aufgedeckt (dh vermutlich μ ^ A - μ ^ 0 = E). Jetzt ist A unser neuer Standard, und wir möchten sicherstellen, dass B A nicht unterlegen ist. Eine andere Möglichkeit, μB - μA ≤ - Δ (Nullhypothese) zu schreiben, ist μB ≤ μA - Δ. Wenn wir annehmen, dass das Tun gleich oder größer als E ist, dann ist μB ≤ μA - E ≤ Placebo. Jetzt sehen wir, dass unsere Schätzung für μB μA - E vollständig überschreitet, wodurch die Nullhypothese vollständig widerlegt wird und wir den Schluss ziehen können, dass B A nicht unterlegen ist, gleichzeitig aber μB ≤ μ Placebo sein kann, dies jedoch nicht Was brauchen wir? (Abbildung 3).
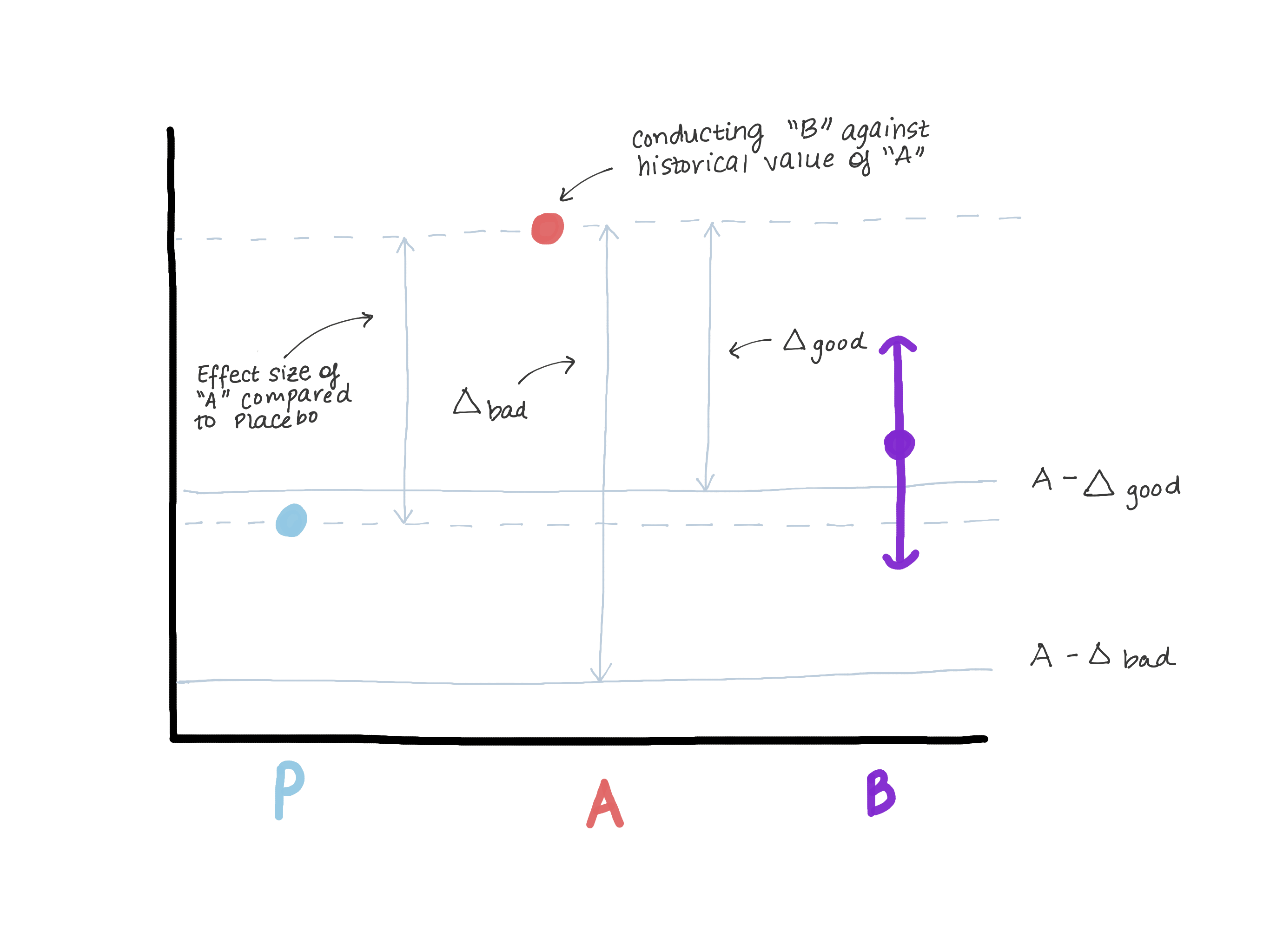Abbildung 3. Demonstration der Risiken bei der Auswahl einer Grenze mit nicht geringerer Effizienz. Wenn die Grenze zu groß ist, können wir schließen, dass B A nicht unterlegen ist, aber gleichzeitig nicht von Placebo zu unterscheiden ist. Wir werden das Medikament, das eindeutig wirksamer als Placebo (A) ist, nicht gegen das Medikament austauschen, das die gleiche Wirksamkeit wie Placebo hat.Α wählen
Wir gehen zur Wahl von α über. Sie können den Standardwert α = 0,05 verwenden, dies ist jedoch nicht ganz ehrlich. Wenn Sie beispielsweise etwas im Internet kaufen und mehrere Rabattcodes gleichzeitig verwenden, obwohl diese nicht zusammengefasst werden sollten, hat der Entwickler nur einen Fehler gemacht und Sie sind damit durchgekommen. Gemäß den Regeln sollte der Wert von α gleich der Hälfte des Wertes von α sein, der zum Testen der Hypothese der Überlegenheit verwendet wird, d. H. 0,05 / 2 = 0,025.
Stichprobengröße
Wie schätze ich die Stichprobengröße? Wenn Sie glauben, dass der wahre durchschnittliche Unterschied zwischen A und B 0 ist, ist die Berechnung der Stichprobengröße dieselbe wie beim Testen der Hypothese der Überlegenheit, außer dass Sie die Effektgröße durch eine Grenze von nicht weniger Effizienz ersetzen, vorausgesetzt, Sie Verwenden Sie
α nicht weniger Effizienz = 1/2 Überlegenheit (
α Nicht -Unterlegenheit = 1/2 Überlegenheit). Wenn Sie Grund zu der Annahme haben, dass Option B möglicherweise etwas schlechter als Option A ist, Sie aber beweisen möchten, dass sie um nicht mehr als Δ schlechter ist, dann haben Sie Glück! Tatsächlich reduziert dies die Größe Ihrer Stichprobe, da es einfacher ist zu zeigen, dass B schlechter als A ist, wenn Sie wirklich denken, dass es etwas schlechter und nicht gleichwertig ist.
Lösungsbeispiel
Angenommen, Sie möchten ein Upgrade auf Version B durchführen, sofern es auf einer 5-Punkte-Kundenzufriedenheitsskala nicht mehr als 0,1 Punkte schlechter als Version A ist. Wir werden diese Aufgabe anhand der Überlegenheitshypothese angehen.
Um die Hypothese der Überlegenheit zu testen, würden wir die Stichprobengröße wie folgt berechnen:
Das heißt, wenn Sie 2103 Beobachtungen in Ihrer Gruppe haben, können Sie zu 90% sicher sein, dass Sie einen Effekt von 0,10 oder mehr finden. Wenn Ihnen der Wert 0,10 jedoch zu groß ist, sollten Sie die Hypothese der Überlegenheit möglicherweise nicht testen. Aus Gründen der Zuverlässigkeit entscheiden Sie sich möglicherweise, eine Studie für eine kleinere Effektgröße durchzuführen, z. B. 0,05. In diesem Fall benötigen Sie 8407 Beobachtungen, dh die Stichprobe erhöht sich fast um das Vierfache. Was aber, wenn wir an unserer ursprünglichen Stichprobengröße festhalten, aber die Leistung auf 0,99 erhöhen, damit wir nicht daran zweifeln, ob wir ein positives Ergebnis erzielen? In diesem Fall ist n für eine Gruppe 3676, was besser ist, aber die Stichprobengröße um mehr als 50% erhöht. Infolgedessen können wir die Nullhypothese trotzdem nicht widerlegen und erhalten keine Antwort auf unsere Frage.
Was ist, wenn wir stattdessen die Hypothese einer nicht geringeren Wirksamkeit testen?
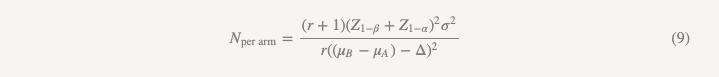
Die Stichprobengröße wird mit Ausnahme des Nenners nach derselben Formel berechnet.
Die Unterschiede zur Formel zum Testen der Überlegenheitshypothese sind wie folgt:
- Z1 - α / 2 wird durch Z1 - α ersetzt, aber wenn Sie alles gemäß den Regeln tun, ersetzen Sie α = 0,05 durch α = 0,025, dh dies ist dieselbe Zahl (1,96).
- erscheint im Nenner (μB - μA)
- θ (Stärke des Effekts) wird durch Δ (Grenze der nicht geringeren Effizienz) ersetzt.
Wenn wir annehmen, dass µB = µA ist, dann ist (µB - µA) = 0 und die Berechnung der Probengröße für eine Grenze von nicht weniger Effizienz genau das, was wir bei der Berechnung der Überlegenheit für den Effektwert von 0,1 erhalten würden, großartig! Wir können eine Studie derselben Größenordnung mit unterschiedlichen Hypothesen und einem unterschiedlichen Ansatz für Schlussfolgerungen durchführen und erhalten eine Antwort auf die Frage, die wir wirklich beantworten möchten.
Nehmen wir nun an, wir glauben nicht wirklich, dass µB = µA und
Wir denken, dass µB etwas schlechter ist, vielleicht 0,01 Einheiten. Dies erhöht unseren Nenner und reduziert die Stichprobengröße pro Gruppe auf 1737.
Was passiert, wenn Version B tatsächlich besser ist als Version A? Wir widerlegen die Nullhypothese, dass B um mehr als Δ schlechter als A ist, und akzeptieren die alternative Hypothese, dass B, wenn es schlechter ist, nicht schlechter als Δ ist und besser sein könnte. Versuchen Sie, diese Schlussfolgerung in eine funktionsübergreifende Präsentation zu bringen, und sehen Sie, was daraus wird (im Ernst, probieren Sie es aus). In einer Situation, in der Sie sich auf die Zukunft konzentrieren müssen, möchte niemand zustimmen, "um nicht mehr als Δ schlechter und möglicherweise besser".
In diesem Fall können wir eine Studie durchführen, die sehr kurz als "Testen der Hypothese, dass eine der Optionen der anderen überlegen oder unterlegen ist" bezeichnet wird. Es werden zwei Sätze von Hypothesen verwendet:
Der erste Satz (der gleiche wie beim Testen der Hypothese einer nicht geringeren Effizienz):
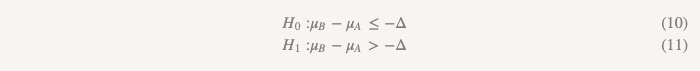
Der zweite Satz (der gleiche wie beim Testen der Hypothese der Überlegenheit):
Wir testen die zweite Hypothese nur, wenn die erste abgelehnt wird. Bei sequentiellen Tests behalten wir das Gesamtfehlerniveau der ersten Art (α) bei. In der Praxis kann dies erreicht werden, indem ein 95% -Konfidenzintervall für die Differenz zwischen den Mitteln erstellt und überprüft wird, um festzustellen, ob das gesamte Intervall -Δ überschreitet. Wenn das Intervall -Δ nicht überschreitet, können wir den Nullwert nicht verwerfen und anhalten. Wenn das gesamte Intervall tatsächlich −Δ überschreitet, fahren wir fort und prüfen, ob das Intervall 0 enthält.
Es gibt eine andere Art von Forschung, die wir nicht diskutiert haben - Äquivalenzstudien.
Studien dieser Art können durch Studien ersetzt werden, um die Hypothese einer nicht geringeren Wirksamkeit zu testen und umgekehrt, aber sie selbst haben einen wichtigen Unterschied. Ein Test zum Testen der Hypothese einer nicht geringeren Effizienz soll zeigen, dass Option B mindestens so gut wie A ist. Eine Äquivalenzstudie soll zeigen, dass Option B mindestens so gut wie A ist, und Option A ist so gut wie B, was komplizierter ist. Im Wesentlichen versuchen wir festzustellen, ob das gesamte Konfidenzintervall für die Mittelwertdifferenz zwischen −Δ und Δ liegt. Solche Studien erfordern eine größere Stichprobe und sind weniger häufig. Wenn Sie das nächste Mal eine Studie durchführen, in der Ihre Hauptaufgabe darin besteht, sicherzustellen, dass die neue Version nicht schlechter ist, geben Sie sich daher nicht mit der "Unfähigkeit zufrieden, die Nullhypothese zu widerlegen". Wenn Sie eine wirklich wichtige Hypothese testen möchten, ziehen Sie verschiedene Optionen in Betracht.