Das Buch "Maschinelles Lernen: Algorithmen für Unternehmen"

Hallo habrozhiteli! Marcos Lopez de Prado teilt das, was sie normalerweise verbergen - die profitabelsten Algorithmen für maschinelles Lernen, mit denen er seit zwei Jahrzehnten große Pools von Fonds der anspruchsvollsten Investoren verwaltet.

Maschinelles Lernen verändert fast jeden Aspekt unseres Lebens. MO-Algorithmen führen Aufgaben aus, denen bis vor kurzem nur vertrauenswürdige Experten vertrauten. In naher Zukunft wird maschinelles Lernen die Finanzen dominieren, Wahrsagerei wird der Vergangenheit angehören und Investitionen werden nicht länger gleichbedeutend mit Glücksspiel sein.

Nutzen Sie die Gelegenheit, an der „maschinellen Revolution“ teilzunehmen. Hierfür reicht es aus, sich mit dem ersten Buch vertraut zu machen, das eine vollständige und systematische Analyse der Methoden des maschinellen Lernens in Bezug auf Finanzen bietet: Beginnen Sie mit Finanzdatenstrukturen, markieren Sie die Finanzreihen, wiegen Sie die Stichprobe, differenzieren Sie die Zeitreihen ... und enden Sie mit Der gesamte Teil widmete sich dem korrekten Backtesting von Anlagestrategien.

Auszug. Risikostrategien verstehen

15.1. Relevanz

Anlagestrategien werden häufig in Bezug auf gehaltene Positionen umgesetzt, bis eine der beiden Bedingungen erfüllt ist: 1) die Bedingung für das Verlassen der Position mit Gewinnen (Gewinnmitnahmen) oder 2) die Bedingung für das Verlassen der Position mit Verlusten (Stoppen des Verlusts). Selbst wenn die Strategie nicht ausdrücklich einen Verluststopp deklariert, gibt es immer ein implizites Verluststopplimit, bei dem der Anleger seine Position nicht mehr finanzieren kann (Margin Call) oder Schaden erleidet, der durch einen Anstieg des nicht realisierten Verlusts verursacht wird. Da die meisten Strategien (explizit oder implizit) diese beiden Ausgangsbedingungen haben, ist es sinnvoll, die Verteilung der Ergebnisse durch einen Binomialprozess zu modellieren. Dies hilft uns wiederum zu verstehen, welche Kombinationen von Wettquoten, Risiken und Auszahlungen unwirtschaftlich sind. Der Zweck dieses Kapitels besteht darin, Ihnen bei der Bewertung zu helfen, wann eine Strategie für kleine Änderungen einer dieser Größen anfällig ist.

Stellen Sie sich eine Strategie vor, die n identisch verteilte, voneinander unabhängige Wetten pro Jahr erzeugt, wobei das Ergebnis Xi der Wette i ∈ [1, n] der Gewinn π> 0 mit der Wahrscheinlichkeit P [Xi = π] = p und der Verlust –π mit der Wahrscheinlichkeit P [Xi ist = –Π] = 1 - p. Sie können sich p als die Genauigkeit eines binären Klassifikators vorstellen, bei dem ein positives Ergebnis das Wetten auf eine Chance und ein negatives Ergebnis das Fehlen einer Chance bedeutet: Wahre Aussagen werden belohnt, falsche Aussagen werden bestraft und negative Ergebnisse (ob wahr oder falsch) haben keine Auszahlungen. Da die Ergebnisse der Wetten {Xi} i = 1, ..., n unabhängig sind, berechnen wir die erwarteten Momente pro Wette. Der erwartete Gewinn aus einer Wette ist E [Xi] = πp + (–π) (1 - p) = π (2p - 1). 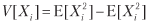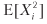Die Varianz ist wo = π2p + (–π) 2 (1 - p) = π2, daher ist V [Xi] = π2 - π2 (2p - 1) 2 = π2 [1– (2p - 1) 2] = 4π2p (1 - p ) Für n identisch verteilte, voneinander unabhängige Raten pro Jahr beträgt das durchschnittliche jährliche Sharpe-Verhältnis (θ)


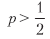
Beachten Sie, wie π die obige Gleichung ausgleicht, da die Auszahlungen symmetrisch sind. Wie im Gaußschen Fall kann θ [p, n] als neu skalierter t-Wert1 verstanden werden. Dies zeigt die Tatsache, dass auch für kleine Das Sharpe-Verhältnis kann für ein ausreichend großes n hoch gemacht werden. Dies dient als wirtschaftliche Grundlage für den Hochfrequenzhandel, bei dem p etwas höher als 0,5 sein kann und der Schlüssel für eine erfolgreiche Börsenaktivität ein Anstieg von n ist. Das Sharpe-Verhältnis ist eine Funktion der Genauigkeit und nicht der Korrektheit, da das Fehlen einer Gelegenheit (negative Aussage) nicht direkt belohnt oder bestraft wird (obwohl zu viele negative Aussagen zu einem kleinen n führen können, wodurch der Sharpe-Koeffizient auf Null reduziert wird).

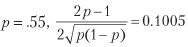
Zum Beispiel für und um eine durchschnittliche jährliche Sharpe Ratio von 2 zu erreichen, sind 396 Wetten pro Jahr erforderlich. Listing 15.1 überprüft dieses Ergebnis experimentell. Abbildung 15.1 zeigt das Sharpe-Verhältnis als Funktion der Genauigkeit für verschiedene Einsatzfrequenzen.

Listing 15.1. Sharpe Ratio in Abhängigkeit von der Anzahl der Wetten

out,p=[],.55 for i in xrange(1000000): rnd=np.random.binomial(n=1,p=p) x=(1 if rnd==1 else -1) out.append(x) print np.mean(out),np.std(out),np.mean(out)/np.std(out) 

Diese Gleichung drückt den Kompromiss zwischen Genauigkeit (p) und Frequenz (n) für einen gegebenen Sharpe-Koeffizienten (θ) ziemlich deutlich aus. Um beispielsweise eine durchschnittliche jährliche Sharpe-Ratio von 2 für eine Strategie zu erhalten, die nur wöchentliche Raten (n = 52) erzeugt, ist eine ziemlich hohe Genauigkeit p = 0,6336 erforderlich.

15.3. Asymmetrische Zahlungen

Stellen Sie sich eine Strategie vor, die n identisch verteilte, voneinander unabhängige Wetten pro Jahr erzeugt, wobei das Ergebnis Xi der Wette i ∈ [1, n] π + mit der Wahrscheinlichkeit P [Xi = π +] = p und das Ergebnis π– (π– <π +) ist ) geschieht mit der Wahrscheinlichkeit P [Xi = π_] = 1 - p. Der erwartete Gewinn aus einer Wette ist E [Xi] = pπ + + (1 - p) π– = (π + - π–) p + π–. Die Dispersion ist V [Xi] =, wobei



Schließlich können wir die vorherige Gleichung für 0 ≤ p ≤ 1 lösen und erhalten


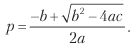
wo:
a = (n + θ2) (π + - π–) 2;
b = [2nπ - θ2 (π + - π -)] (π + - π–);


Hinweis: Listing 15.2 überprüft diese symbolischen Vorgänge mithilfe der Python SymPy Live-Shell, die im Cloud-Dienst von Google App Engine ausgeführt wird: live.sympy.org .

Listing 15.2. Verwenden der SymPy-Bibliothek für symbolische Operationen

 >>> from sympy import * >>> init_printing(use_unicode=False,wrap_line=False,no_global=True) >>> p,u,d=symbols('pu d') >>> m2=p*u**2+(1-p)*d**2 >>> m1=p*u+(1-p)*d >>> v=m2-m1**2 >>> factor(v) 

Die obige Gleichung beantwortet die folgende Frage: Welcher Genauigkeitsgrad p ist für eine gegebene Handelsregel, die durch die Parameter {π–, π +, n} gekennzeichnet ist, erforderlich, um das Sharpe-Verhältnis gleich θ * zu erreichen? Um beispielsweise θ = 2 für n = 260, π– = –.01, π + = .005 zu erhalten, benötigen wir p = .72. Aufgrund der großen Anzahl von Wetten hat eine sehr kleine Änderung von p (von p = 0,7 auf p = 0,72) das Sharpe-Verhältnis von θ = 1,173 auf θ = 2 gefördert. Andererseits zeigt dies auch, dass diese Strategie für kleine anfällig ist Änderungen in p. Listing 15.3 implementiert die Ableitung der erwarteten Genauigkeit. In Abb. 15.2 zeigt die angenommene Genauigkeit als Funktion von n und π–, wobei π + = 0,1 und θ * = 1,5 ist. Wenn der Schwellenwert π– für ein gegebenes n negativer wird, ist ein höherer Grad p erforderlich, um θ * für einen gegebenen Schwellenwert π + zu erreichen. Wenn die Zahl n für einen gegebenen Schwellenwert π– kleiner wird, ist ein höherer Grad von p erforderlich, um θ * für einen gegebenen π + zu erreichen.

Listing 15.3. Berechnung der geschätzten Genauigkeit

 def binHR(sl,pt,freq,tSR): ´´´ 

Welche Mindestgenauigkeit ist für eine bestimmte Handelsregel, die durch die Parameter {sl, pt, freq} gekennzeichnet ist, erforderlich, um das Sharpe-Verhältnis von tSR zu erreichen?

1) Eingänge
sl: Verluststoppschwelle
pt: Gewinnschwelle
Frequenz: Die Anzahl der Wetten pro Jahr
tSR: Zieljahresdurchschnitt der Sharpe Ratio
2) Beenden
p: Mindestgenauigkeit p erforderlich, um tSR zu erreichen
´´´
a = (freq + tSR ** 2) * (pt-sl) ** 2
b = (2 * freq * sl-tSR ** 2 * (pt-sl)) * (pt-sl)
c = freq * sl ** 2
p = (- b + (b ** 2-4 * a * c) **. 5) / (2. * a)
return p


Listing 15.4 löst θ [p, n, π–, π +] für die geschätzte Wettfrequenz n. In Abb. 15.3 zeigt die geschätzte Frequenz in Abhängigkeit von p und π–, wobei π + = 0,1 und θ * = 1,5 ist. Wenn der Schwellenwert π– für einen gegebenen Grad p negativer wird, ist eine höhere Zahl n erforderlich, um θ * für einen gegebenen Schwellenwert π + zu erreichen. Wenn der Grad p für einen gegebenen Schwellenwert π– kleiner wird, ist eine höhere Zahl n erforderlich, um θ * für einen gegebenen Schwellenwert π + zu erreichen.

Listing 15.4. Berechnung der geschätzten Wettfrequenz

 def binFreq(sl,pt,p,tSR): ´´´ 

Wie viele Wetten pro Jahr sind für eine gegebene Handelsregel, die durch die Parameter {sl, pt, freq} gekennzeichnet ist, erforderlich, um den Sharp-Koeffizienten tSR mit einem Genauigkeitsgrad p zu erreichen?

Hinweis: Gleichung mit Radikalen, auf Fremdlösungen prüfen.

1) Eingänge
sl: Verluststoppschwelle
pt: Gewinnschwelle
p: Genauigkeitsgrad p
tSR: Zieljahresdurchschnitt der Sharpe Ratio
2) Beenden
freq: Die Anzahl der pro Jahr benötigten Wetten
´´´
freq = (tSR * (pt-sl)) ** 2 * p * (1-p) / ((pt-sl) * p + sl) ** 2 # möglicherweise irrelevant
wenn nicht np.isclose (binSR (sl, pt, freq, p), tSR): return
Rückgabefrequenz



»Weitere Informationen zum Buch finden Sie auf der Website des Herausgebers
» Inhalt
» Auszug

25% Rabatt-Gutschein für Straßenhändler - Maschinelles Lernen

Nach Zahlung der Papierversion des Buches wird eine elektronische Version des Buches per E-Mail verschickt.