Hallo Habr!
Als
Gesetzgeber für
Einheit auf dem russischen Markt bieten wir Ihnen an, eine interessante Studie über die praktische Anwendung des WFC-Algorithmus (Wave Function Collapse) zu lesen, die auf dem Bild und der Ähnlichkeit des bekannten Prinzips der Quantenmechanik basiert und für die prozedurale Erzeugung von Levels in Spielen sehr praktisch ist. Zuvor hatte Habré die
detaillierte Geschichte über diesen Algorithmus bereits veröffentlicht. Der Autor des heutigen Artikels, Marian Kleineberg, betrachtet den Algorithmus im Kontext dreidimensionaler Grafiken und der Erzeugung einer endlosen Stadt. Viel Spaß beim Lesen!
Wir werden über ein Spiel sprechen, bei dem Sie durch eine endlose Stadt gehen, die prozedural generiert wird, während Sie sich bewegen. Eine Stadt wird aus einer Reihe von Blöcken unter Verwendung des WFC-Algorithmus (Wellenfunktionskollaps) aufgebaut.
Die spielbare Baugruppe kann auf der Website
itch.io heruntergeladen werden. Sie können den
Quellcode auch auf github verwenden . Schließlich schlage ich ein
Video vor, in dem ich durch die so erzeugte Stadt gehe.
Algorithmus
Ich werde das Wort "Zelle" ein 3D-Voxelnetzelement nennen, das einen Block enthalten oder leer sein kann. Das Wort "Modul" werde ich einen Block nennen, der eine solche Zelle belegen kann.
Der Algorithmus entscheidet, welche Module in jeder Zelle der Spielwelt ausgewählt werden sollen. Ein Array von Zellen wird als Wellenfunktion in einer nicht beobachtbaren Form betrachtet. Somit entspricht jede Zelle vielen Modulen, die darin erscheinen können. In Bezug auf die Quantenmechanik könnte man sagen: "Die Zelle befindet sich in einer Überlagerung aller Module." Die Existenz der Welt beginnt in einer völlig unbeobachtbaren Form, in der sich jedes Modul in jeder Zelle befinden kann. Ferner kollabieren alle Zellen nacheinander. Dies bedeutet, dass für jede Zelle ein Modul zufällig aus allen möglichen ausgewählt wird.
Der nächste Schritt ist die Weitergabe von Einschränkungen. Für jedes Modul wird eine Teilmenge von Modulen ausgewählt, die benachbart sein dürfen. Jedes Mal, wenn ein Modul zusammenbricht, werden Teilmengen anderer Module aktualisiert, die weiterhin als angrenzend zulässig sind. Die Ausbreitungsstufe von Einschränkungen ist hinsichtlich der Rechenleistung der ressourcenintensivste Teil des Algorithmus.
Ein wichtiger Aspekt des Algorithmus ist die Bestimmung der zu kollabierenden Zelle. Der Algorithmus kollabiert die Zelle immer mit der
kleinsten Entropie . Dies ist eine Zelle, die eine minimale Anzahl von Auswahlmöglichkeiten zulässt (dh eine Zelle mit der geringsten Zufälligkeit). Wenn die Wahrscheinlichkeit eines Zusammenbruchs für alle Module gleich ist, hat die Zelle mit der minimalen Anzahl möglicher Module die niedrigste Entropie. In der Regel sind die Auswahlwahrscheinlichkeiten für die verschiedenen verfügbaren Module unterschiedlich. Eine Zelle mit zwei möglichen Modulen mit derselben Wahrscheinlichkeit bietet eine größere Auswahl (größere Entropie) als diejenige, in der zwei Module vorhanden sind, und für eines von ihnen ist die Wahrscheinlichkeit, unter die Auswahl zu fallen, sehr hoch und für das andere sehr gering.

(Gif gepostet von
ExUtumno auf Github)
Nähere Informationen zum Wellenfunktionskollapsalgorithmus sowie einige schöne Beispiele finden Sie hier. Ursprünglich wurde dieser Algorithmus vorgeschlagen, um 2D-Texturen basierend auf einer einzelnen Probe zu erzeugen. In diesem Fall werden die Wahrscheinlichkeitsindikatoren der Module und Adjazenzregeln in Abhängigkeit von ihrem Auftreten im Beispiel bestimmt. Dieser Artikel enthält diese Informationen manuell.
Hier ist ein
Video , das diesen Algorithmus in Aktion demonstriert.
Über Blöcke, Prototypen und Module
Die Welt wird aus einer Menge von ungefähr 100 Blöcken erzeugt. Ich habe sie mit Blender erstellt. Anfangs hatte ich nur sehr wenige Blöcke und fügte sie nach und nach hinzu, wenn ich es für notwendig hielt.

Der Algorithmus muss wissen, welche Module nebeneinander angeordnet werden können. Für jedes Modul gibt es 6 Listen möglicher Nachbarn, eine in jeder Richtung. Ich wollte jedoch vermeiden, eine solche Liste manuell erstellen zu müssen. Außerdem wollte ich automatisch gedrehte Optionen für jeden meiner Blöcke generieren.
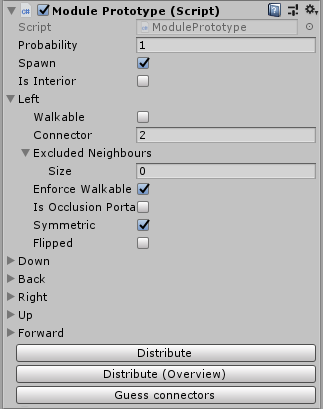
Beide Aufgaben werden mit den sogenannten Prototypmodulen gelöst. Im Wesentlichen ist dies
MonoBehaviour , mit dem Sie im Unity-Editor bequem arbeiten können. Auf der Grundlage solcher Prototypen werden automatisch Module zusammen mit Listen gültiger benachbarter Elemente und gedrehten Optionen erstellt.
Bei der Modellierung von Adjazenzinformationen trat ein komplexes Problem auf, so dass dieser automatische Prozess funktionierte. Folgendes habe ich bekommen:

Jeder Block hat 6 Kontakte, einen für jede Fläche. Der Kontakt hat eine Nummer. Zusätzlich können die horizontalen Kontakte invertiert, nicht invertiert oder symmetrisch sein. Vertikale Kontakte haben entweder einen Rotationsindex im Bereich von 0 bis 3 oder sind als
rotationsinvariant markiert.
Auf dieser Grundlage kann ich automatisch überprüfen, welche Module zusammenpassen dürfen. Angrenzende Module müssen die gleichen Pin-Nummern haben. Ihre Symmetrie muss ebenfalls übereinstimmen (der gleiche vertikale Rotationsindex, ein Paar invertierter und nicht invertierter horizontaler Kontakte), oder die Module müssen symmetrisch / invariant sein.
Es gibt Ausschlussregeln, nach denen ich Nachbarschaftsoptionen verbieten kann, die standardmäßig zulässig sind. Einige Blöcke mit passenden Kontakten sehen in der Nähe einfach hässlich aus. Hier ist ein Beispiel für eine Karte, die ohne Anwendung von Ausnahmeregeln erstellt wurde:

Weg zur Unendlichkeit
Der ursprüngliche Wellenfunktionskollapsalgorithmus erzeugt Karten mit endlicher Größe. Ich wollte eine Welt bauen, die sich immer weiter ausdehnt, wenn Sie sich darauf bewegen.
Zuerst habe ich versucht, Fragmente endlicher Größe zu erzeugen und die Kontakte benachbarter Fragmente als Einschränkungen zu verwenden. Wenn ein Fragment generiert wird und auch ein angrenzendes Fragment generiert wird, sind nur solche Module zulässig, die neben vorhandene Module passen. Bei diesem Ansatz tritt das folgende Problem auf: Wenn eine Zelle zusammenbricht, verringert die Ausbreitung von Beschränkungen die Möglichkeiten selbst in einer Entfernung von mehreren Zellen. Das folgende Bild zeigt die Auswirkungen des Zusammenbruchs einer einzelnen Zelle:

Wenn bei jedem Schritt des Algorithmus nur ein Fragment generiert wird, gelten die Einschränkungen nicht für benachbarte Fragmente. In diesem Fall wurden solche Module innerhalb des Fragments ausgewählt, die nicht akzeptabel wären, wenn andere Fragmente berücksichtigt würden. Als der Algorithmus versuchte, das nächste Fragment zu generieren, konnte er daher keine einzige Lösung finden.
Jetzt verwende ich keine Fragmente mehr, sondern speichere die Karte in einem Wörterbuch, das die Position einer Zelle in einer Zelle anzeigt. Die Zelle wird nur bei Bedarf gefüllt. Einige Elemente des Algorithmus sollten vor diesem Hintergrund angepasst werden. Bei der Auswahl einer Zelle, die kollabieren soll, können nicht alle Zellen berücksichtigt werden, wenn ihre Anzahl unendlich ist. Stattdessen generieren wir jeweils nur einen kleinen Teil der Karte, sobald der Spieler sie erreicht hat. Außerhalb dieses Gebiets breiten sich die Beschränkungen weiter aus.
In einigen Fällen funktioniert dieser Ansatz nicht. Betrachten Sie eine Reihe von Modulen für einen geraden Abschnitt eines Tunnels aus der obigen Abbildung - es gibt keinen Zugang zum Tunnel. Wenn der Algorithmus ein solches Tunnelmodul auswählt, ist der Tunnel per Definition unendlich. In der Phase der Verteilung von Beschränkungen wird das Programm versuchen, eine unendliche Anzahl von Zellen zuzuweisen. Ich habe einen speziellen Satz von Modulen entwickelt, um dieses Problem zu umgehen.
Randbedingungen
Es gibt zwei wichtige Randbedingungen. Alle Gesichter auf der obersten Ebene der Karte müssen Luftkontakte haben. Alle Flächen auf der Basis der Karte müssen „feste“ Kontakte haben. Wenn diese Bedingungen nicht erfüllt sind, befinden sich auf der Karte Löcher im Boden, und einige Gebäude haben kein Dach.
Auf einer Karte endlicher Größe wäre dieses Problem leicht zu lösen. Für alle Zellen auf der höchsten und niedrigsten Ebene müssten alle Module mit ungeeigneten Kontakten entfernt werden. Starten Sie dann die Verteilung der Einschränkungen und entfernen Sie die verbleibenden Module, die nicht mehr zu uns passen.
Auf einer Karte mit unendlicher Größe funktioniert dies nicht, da wir sowohl auf der höchsten als auch auf der niedrigsten Ebene eine unendliche Anzahl von Zellen haben. Die naivste Lösung besteht darin, alle unangemessenen Zellen sofort zu löschen, sobald sie entstehen. Wenn ein Modul auf der oberen Ebene entfernt wird, gelten jedoch Einschränkungen für die angrenzenden Zellen. Es gibt einen Lawineneffekt, der wiederum zu einer unendlichen Auswahl von Zellen führt.
Ich habe dieses Problem gelöst, indem ich eine 1 × n × 1-Karte erstellt habe, wobei n die Höhe ist. Diese Karte verwendet World Wrapping, um Einschränkungen zu verbreiten. Der Mechanismus funktioniert wie im Spiel Pacman: Wenn der Charakter über den rechten Rand der Karte hinausgeht, kehrt er aufgrund des linken Randes dorthin zurück. Jetzt kann ich meine Karte einschränken. Jedes Mal, wenn Sie eine neue Zelle auf einer unendlichen Karte erstellen, wird diese Zelle mit einer Reihe von Modulen initialisiert, die einer bestimmten Position auf der Karte entsprechen.
Fehlerbedingungen und Rücksuche
Manchmal erreicht der WFC-Algorithmus einen Zustand, in dem die Zelle keinem möglichen Modul entspricht. In Anwendungen, in denen es sich um eine Welt endlicher Größe handelt, können Sie das Ergebnis einfach zurücksetzen und von vorne beginnen. In einer unendlichen Welt wird dies nicht funktionieren, da dem Spieler bereits ein Teil der Welt gezeigt wird. Zuerst entschied ich mich für eine Lösung, bei der die Stellen, an denen die Fehler auftraten, mit weißen Blöcken gefüllt waren.
Ich verwende derzeit die Rückgabesuche. Die Reihenfolge des Zusammenbruchs der Zellen und einige Informationen über die Verteilung der Einschränkungen werden in Form eines Verlaufs gespeichert. Wenn der WFC-Algorithmus fehlschlägt, wird ein Teil des Verlaufs abgebrochen. In der Regel funktioniert dies, aber manchmal können Fehler zu spät erkannt werden, und eine Rückgabesuche umfasst viele Schritte. In seltenen Fällen wird die Zelle, in der sich der Spieler befindet, regeneriert.
Aufgrund dieser Einschränkung ist die Anwendung des WFC-Algorithmus mit unendlichen Welten meiner Meinung nach nicht für kommerzielle Spiele geeignet.
Hintergrund
Ich begann an dieser Aufgabe zu arbeiten, nachdem ich einen
Vortrag von Oscar Stelberg gesehen hatte , in dem er erzählte, wie er den Algorithmus verwendet, um Levels im Spiel Bad North zu generieren. Im Allgemeinen wurde mein Algorithmus während der
Procjam- Woche
implementiert .
Ich habe einige Ideen für eine weitere Verfeinerung dieses Algorithmus, bin mir aber nicht sicher, ob ich eines Tages das Gameplay hinzufügen werde. Und wenn ich zusammenkomme, wird es sicher keine so epische Strategie sein, wie Sie es sich bereits vorgestellt haben. Wenn Sie jedoch überprüfen möchten, wie Ihre Lieblingsspielmechanik mit diesem Algorithmus funktioniert, probieren Sie es einfach selbst aus! Am Ende ist der Quellcode öffentlich verfügbar und vom MIT lizenziert.