Talent vs. Glück: Die Rolle des Zufalls für Erfolg und Misserfolg

Kürzlich stieß ich auf eine interessante Arbeit italienischer Wissenschaftler über die stark unterschätzte Rolle von Glück und Zufall in unserem Leben. Leider habe ich die Vollversion nicht auf Russisch gefunden (vielleicht sah ich schlecht aus?), Aber ich wollte wirklich mit meinen nicht fließenden englischen Kameraden teilen, was ich gelesen habe. Deshalb krempelte er die Ärmel hoch und machte sich an seine handwerkliche Übersetzung. Die Autoren Alessandro, Alessio und Andrea haben es freundlicherweise gestattet, es öffentlich zu veröffentlichen. Wenn Sie interessiert sind, sind Sie bei cat willkommen.

Die Autoren

• A. Pluchino - Institut für Physik und Astronomie, Universität Catania und Zweigstelle Catania des Nationalen Instituts für Kernphysik, Italien; alessandro.pluchino@ct.infn.it
• A. E. Biondo - Institut für Wirtschaftswissenschaften, Universität Catania, Italien; ae.biondo@unict.it
• A. Rapisard - Institut für Physik und Astronomie, Universität Catania und Zweigstelle Catania des Nationalen Instituts für Kernphysik, Italien; Zentrum für das Studium komplexer Systeme, Wien; andrea.rapisarda@ct.infn.it

Anmerkung

Das vorherrschende meritokratische Modell der westlichen Kulturen beruht zu einem großen Teil auf der vorherrschenden meritokratischen ( Meritokratie ist das Prinzip der Regierungsführung, nach der die fähigsten Menschen, unabhängig von ihrer sozialen Herkunft und ihrem finanziellen Wohlstand ) Führungsposition, auf der Überzeugung, dass Erfolg hauptsächlich, wenn nicht sogar vollständig, Erfolg ist. hängt von persönlichen Qualitäten wie Talent, Intelligenz, Fähigkeiten, Einfallsreichtum, harter Arbeit, Ausdauer, harter Arbeit oder Risikobereitschaft ab. Manchmal sind wir bereit zuzugeben, dass ein gewisser Teil des Glücks auch dazu beitragen kann, einen signifikanten materiellen Erfolg zu erzielen. In Wahrheit wird die Bedeutung externer Kräfte in einzelnen Erfolgsgeschichten jedoch häufig unterschätzt. Es ist bekannt, dass Intelligenz (oder allgemein Talent und persönliche Qualitäten) in einer Bevölkerung eine Gaußsche Verteilung aufweist, während die Verteilung von Werten - oft als Erfolgsmaßstab angesehen - normalerweise einem Machtgesetz (Pareto-Gesetz) folgt, wenn die Mehrheit arm ist und Es gibt eine vernachlässigbare Anzahl von Milliardären. Diese Diskrepanz zwischen normalverteilten Eingaben mit normalem Pegel (gemitteltes Talent oder Intelligenz) und einer konstanten Verteilung am Ausgang lässt darauf schließen, dass sich irgendwo hinter den Kulissen eine unsichtbare Komponente befindet. In diesem Artikel gehen wir auf der Grundlage einer äußerst einfachen und auf Spielzeugagenten basierenden Simulation davon aus, dass eine solche Komponente ein gewöhnlicher Unfall ist. Insbesondere zeigen wir, dass der Erfolg eines Lebens zwar ein gewisses Maß an Talent erfordert, die begabtesten Menschen jedoch fast nie die höchsten Wohlstandsgipfel erreichen und von mittelmäßigen, aber viel erfolgreicheren Persönlichkeiten überholt werden. Soweit wir wissen, war dieses widersprüchliche Ergebnis des gesunden Menschenverstandes - obwohl es in vielen Literaturstellen implizit zwischen den Zeilen angenommen wird - das erste, das eine quantitative Bewertung vorgenommen hat. Auf diese Weise können Sie einen neuen Blick auf die Effektivität der Bewertung der Verdienste auf der Grundlage des bereits erzielten Erfolgs werfen und das Risiko hervorheben, übermäßige Ehrungen oder Ressourcen an Personen weiterzugeben, die auf lange Sicht möglicherweise erfolgreicher sind als andere. Mit diesem Modell betrachten und vergleichen wir auch verschiedene Verhaltenshypothesen, um die effektivsten Strategien für die öffentliche Forschungsfinanzierung aufzuzeigen, mit dem Ziel, Meritokratie, Vielfalt und Innovation zu verbessern.

1. Einleitung

Die Allgegenwart der Machtabhängigkeit in vielen physikalischen, biologischen oder sozioökonomischen komplexen Systemen kann als ein charakteristisches mathematisches Merkmal der engen Beziehung ihrer dynamischen Eigenschaften zu einer skalenveränderten topologischen Struktur angesehen werden [1, 2, 3, 4]. Im sozioökonomischen Kontext ist nach der Arbeit von Pareto [5, 6, 7, 8, 9] bekannt, dass die Verteilung des Reichtums den Charakter einer Machtabhängigkeit hat, deren charakteristische stark verlängerte Form die Tiefe des bestehenden Abgrunds zwischen Arm und Reich unserer Gesellschaft widerspiegelt.

Ein kürzlich veröffentlichter Bericht [10] zeigt, dass diese Kluft heute viel größer ist als befürchtet: Acht Menschen besitzen den gleichen Wohlstand wie 3,6 Milliarden Menschen, die den ärmsten Teil der Menschheit ausmachen. In den letzten 20 Jahren wurden mehrere theoretische Modelle entwickelt, die die Verteilung von Werten im Kontext der Wahrscheinlichkeitstheorie und der physikalischen Statistik berechnen, häufig in Form einer Multi-Agent-Modellierung mit einfacher interner Dynamik [11, 12, 13, 14, 15, 16, 17].

Wenn wir uns weiter in diese Richtung bewegen und persönlichen Reichtum als Maß für den Erfolg betrachten, kann argumentiert werden, dass die zutiefst asymmetrische und ungleiche Verteilung unter den Menschen eine Folge ihrer natürlichen Unterschiede in Talent, Fähigkeiten, Kompetenz, Intelligenz, Fähigkeiten oder dem Maß ihrer Ausdauer, harten Arbeit oder Zielstrebigkeit. Eine solche Annahme in impliziter Form ist die Grundlage des sogenannten meritokratischen Paradigmas: Sie beeinflusst nicht nur die Art und Weise, wie unsere Gesellschaft Beschäftigungsmöglichkeiten, Ehre und Ruhm bietet, sondern auch die Strategien der Regierungen, Ressourcen und Finanzmittel denjenigen zuzuweisen, die als die am meisten angesehenen gelten geehrte Persönlichkeiten.

Die vorherige Schlussfolgerung scheint sich jedoch stark von den bestätigten Daten zu unterscheiden, dass die oben genannten Eigenschaften und Qualitäten von Menschen normalerweise in der Bevölkerung verteilt sind, d. H. Einer symmetrischen Gaußschen Verteilung relativ zu diesem Durchschnitt entsprechen. Zum Beispiel entspricht die durch IQ-Tests gemessene Intelligenz dem folgenden Muster: Der durchschnittliche IQ beträgt 100, aber niemand hat einen IQ von 1000 oder 10000. Gleiches gilt für die in Arbeitsstunden gezählte Arbeit: Jemand arbeitet mehr als der Durchschnitt, ein anderer weniger, aber es gibt niemanden, der milliardenfach mehr Stunden arbeitet als die anderen.

In unserer Zeit gibt es jedoch immer mehr Belege für die grundlegende Rolle von Zufall, Glück oder allgemein zufälligen Faktoren bei der Bestimmung von Erfolg oder Misserfolg in unseren persönlichen und beruflichen Angelegenheiten. Insbesondere wurde gezeigt, dass alle Wissenschaftler die gleiche Chance haben, bahnbrechende Arbeiten während ihrer Karriere zu veröffentlichen [18]; dass diejenigen, deren erster Buchstabe des Familiennamens näher am Anfang des Alphabets liegt, mit größerer Wahrscheinlichkeit die Position eines Abteilungsleiters erhalten [19]; dass sich die von Wissenschaftlern gesammelten Verteilungen bibliometrischer Indikatoren aufgrund des wachsenden Phänomens, das mit dem inflationären Mechanismus „Publish or Die“ verbunden ist, als zufällig und bedeutungslos herausstellen können [20]; dass die Position einer Person in einer alphabetisch sortierten Liste wichtig sein kann, um den Zugang zu öffentlichen Dienstleistungen zu bestimmen, der durch die Anzahl der Plätze begrenzt ist [21]; dass der Anfangsbuchstabe eines zweiten Vornamens eine Einschätzung der intellektuellen Fähigkeiten aufwirft [22]; dass Personen mit leicht ausgesprochenen Namen positiver bewertet werden als Personen mit komplexen Namen [23]; dass diejenigen, deren Namen häufiger aristokratisch klingen als andere, als Führer und nicht als Untergebene arbeiten [24]; dass Frauen mit männlichen Spitznamen in der Anwaltschaft erfolgreicher sind [25]; dass ungefähr die Hälfte der Einkommensunterschiede zwischen Menschen auf der ganzen Welt ausschließlich durch ihr Wohnsitzland und die Verteilung der Gehälter innerhalb des jeweiligen Landes erklärt wird [26]; dass die Wahrscheinlichkeit, Regisseur zu werden, stark von Ihrem Namen und Ihrem Geburtsmonat abhängt [27, 28, 29]; dass innovative Ideen das Ergebnis zufälliger Reaktionen in den Zellen unseres Gehirns sind [30]; und dass selbst die Wahrscheinlichkeit, an Krebs zu erkranken und möglicherweise eine hervorragende Karriere zu zerstören, größtenteils vom Scheitern abhängt [31, 32]. Neuere Arbeiten zum Thema Fortpflanzungserfolg während des gesamten Lebens tragen zur Bestätigung solcher Aussagen bei und zeigen, dass das Leben bestimmter Personen häufig durch Glück bestimmt wird, wenn Abweichungen von Merkmalen das Schicksal der gesamten Bevölkerung beeinflussen können.

In den letzten Jahren haben viele Autoren, darunter der Statistiker und Risikoanalytiker Nassim Taleb [35, 36], der Investmentstratege Michael Mobussin [37] und der Ökonom Robert Frank [38], in einer Reihe populärer Bücher die Beziehung zwischen Glück und Können bei Finanztransaktionen untersucht. Wirtschaft, Sport, Kunst, Musik, Literatur, Wissenschaft und viele andere Bereiche. Sie kamen zu dem Schluss, dass zufällige Ereignisse eine viel größere Rolle im Leben spielen, als sich viele vorgestellt hätten. Tatsächlich gehen sie nicht davon aus, dass Erfolg nicht von Talenten und Anstrengungen abhängt, da in äußerst wettbewerbsintensiven Bereichen oder Märkten wie „Der Gewinner nimmt alles“, in denen wir zu dieser Zeit leben und arbeiten, die produktivsten Menschen fast immer außergewöhnlich sind talentiert und fleißig. Sie kamen nur zu dem Schluss, dass Talent und Anstrengung nicht ausreichen: Sie müssen auch zur richtigen Zeit am richtigen Ort sein. Kurz gesagt, das Glück wirkt sich auch aus, obwohl seine Rolle von erfolgreichen Menschen fast immer unterschätzt wird. Dies liegt an der Tatsache, dass Zufälligkeit oft nicht offensichtlich funktioniert. Daher ist es einfach, Ereignisse, die Erfolg zeigen, als etwas zu vergleichen, das unvermeidlich war. Taleb nennt eine solche Neigung „einen fantastischen Irrtum“ [36], und der Soziologe Paul Lazarsfeld schlug den Begriff „voreingenommene Retrospektive“ vor. In seinem letzten Buch „Alles ist offensichtlich: Wenn Sie die Antwort kennen“ [39] schlägt der Soziologe und Pionier der Netzwerkwissenschaft Duncan Watts vor, dass sowohl fabelhafte Täuschung als auch voreingenommene retrospektive Anziehungskraft auf ein spezielles Phänomen gerichtet sind, bei dem Menschen, die ungewöhnlich erfolgreiche Ergebnisse sehen, Betrachten Sie sie als ein unbestrittenes Produkt harter Arbeit und Talent. Erfolg entsteht jedoch hauptsächlich durch komplexe und miteinander verflochtene Schritte, von denen jeder von den vorherigen abhängt: Wenn einer von ihnen anders wäre, wäre mit ziemlicher Sicherheit auch die gesamte Karriere oder der gesamte Lebensweg anders. Dieses Argument basiert auch auf den Ergebnissen einer innovativen experimentellen Studie, die Watts einige Jahre zuvor in Zusammenarbeit mit anderen Autoren durchgeführt hatte [40], in der der Erfolg bisher unbekannter Songs auf dem Markt für künstliche Musik nicht mit der Qualität des Werks selbst korrelierte. Und dies erschwert natürlich alle Vorhersagen erheblich, wie eine andere, neuere Studie zeigt [41].

In diesem Artikel werden wir versuchen, mithilfe eines agentenbasierten statistischen Ansatzes die Rolle von Glück und Talent in erfolgreichen Karrieren praktisch quantitativ zu bestimmen. In Abschnitt 2 stellen wir auf der Grundlage der Mindestanzahl von Annahmen, nämlich der Gaußschen Natur der Talentverteilung [42] und der multiplikativen Dynamik von Erfolgen und Misserfolgen [43], ein einfaches Modell vor, das wir als „Talent vs. Luck“ -Modell (TPU) bezeichnet haben Dies ahmt die berufliche Entwicklung einer Gruppe von Menschen über den Zeitraum von 40 Jahren ihrer Arbeit nach. Das Modell zeigt, dass Zufälligkeit in der Realität eine grundlegende Rolle bei der Bestimmung der erfolgreichsten Personen spielt. Die wahre Sache ist, dass talentierte Menschen, wie zu erwarten, in ihrem eigenen Leben eher reich, berühmt oder bedeutsam werden als weniger vorbereitete. Aber und diese weniger intuitive Erklärung, gewöhnliche Menschen mit einem gewöhnlichen Talentniveau sind statistisch dazu bestimmt, viel häufiger erfolgreich zu sein (d. H. Am Ende einer gewissen Machtverteilung des Erfolgs zu stehen) als die talentiertesten, vorausgesetzt, sie werden zu Favoriten des Glücks für deines Lebens. Diese Tatsache wird häufig angetroffen, wie in den Referenzen [35, 36, 38] angegeben, aber soweit wir wissen, wurde sie zuerst in dieser Arbeit modelliert und gemessen.

Der Erfolg von Menschen mit gewöhnlichen Talenten stellt das „meritokratische“ Paradigma und all jene Strategien und Mechanismen in Frage, die Menschen, die als die besten auf ihrem Gebiet gelten, mehr Belohnungen, Chancen, Ehre, Ruhm und Ressourcen verliehen [44, 45]. Tatsache ist, dass in den allermeisten Fällen alle Bewertungen des Talents einer Person nachträglich vorgenommen wurden, und zwar ausschließlich anhand ihrer Tätigkeit oder der erzielten Ergebnisse in einem bestimmten Bereich unserer Gesellschaft, wie Sport, Wirtschaft, Finanzen, Kunst , Wissenschaft usw. Diese Art der irreführenden Bewertung führt zu einer Substitution von Ursache und Wirkung, wobei diejenigen als die talentiertesten bewertet werden, die einfach die erfolgreichsten sind [46, 47]. In Übereinstimmung mit dieser Ansicht warnten frühere Arbeiten vor ähnlichen Arten von „Near Meritocracy“ und zeigten die Wirksamkeit anderer Strategien, die auf Zufallsstichproben in vielen verschiedenen Umgebungen wie Management, Politik und Finanzen basieren [48, 49, 50, 51, 52, 53, 54, 55]. In Abschnitt 3 wenden wir unseren Ansatz an und skizzieren, wie die Verteilung öffentlicher Mittel im Rahmen der wissenschaftlichen Forschung möglich ist. Wir untersuchen die Konsequenzen verschiedener Verteilungsstrategien, von denen es eine „nahezu“ meritokratische gibt, mit dem Ziel, neue Wege zu erkunden, um gleichzeitig den Mindesterfolg der talentiertesten Menschen in der Gesellschaft und die Gesamteffektivität der Staatsausgaben zu steigern. Wir werden im Allgemeinen auch untersuchen, wie wichtig die Chancen sind, die die Umwelt in Form von Bildung und Einkommensniveau bietet (d. H. Externe Faktoren in Abhängigkeit vom Land und der sozialen Schicht, aus der die Menschen stammen), um die Erfolgswahrscheinlichkeit zu erhöhen. Abschließende Bemerkungen vervollständigen die Arbeit.

2. Modell

Darüber hinaus schlagen wir ein Agentenmodell namens „Talent gegen Glück“ (TPU) vor, das auf einer kleinen Anzahl von Annahmen basiert und darauf abzielt, die Entwicklung der Karrieren einer Gruppe von Menschen unter dem Einfluss zufällig auftretender erfolgreicher und erfolgloser Ereignisse zu beschreiben.


Abbildung 1: Ein Beispiel für die Anfangsparameter unserer Simulation. Alle in diesem Artikel vorgestellten Simulationen wurden in der NetLogo-Agentensimulationsumgebung durchgeführt [56]. N = 1000 Personen (Agenten) mit unterschiedlichem Talent (Intelligenz, Fähigkeiten usw.), die zufällig über feste Positionen innerhalb der quadratischen Welt von 201 × 201 Abschnitten mit zyklischen Randbedingungen verteilt sind. Während jeder Simulation, die mehrere Jahrzehnte umfasst, sind sie einer bestimmten Anzahl von N _E erfolgreichen (grüne Kreise) und erfolglosen (rote Kreise) Ereignissen ausgesetzt, die sich auf zufälligen Trajektorien um die Welt bewegen (Random Walk). In diesem Beispiel ist N _E = 500.

Wir betrachten N Individuen mit T _i Talent (Intellekt, Fähigkeiten, Fertigkeiten usw.) mit einer Normalverteilung im Intervall [0; 1] um einen gegebenen Durchschnitt m _T mit einer Standardabweichung σ _{T, die} zufällig an festen Positionen innerhalb der quadratischen Welt (siehe Abbildung 1) mit zyklischen Randbedingungen (dh mit einer toroidalen Topologie) platziert und von einer bestimmten Anzahl N _{E von} "beweglich" umgeben ist. Ereignisse (mit Punkten markiert), von denen einige erfolgreich sind, keine anderen (neutrale Ereignisse in diesem Modell werden nicht berücksichtigt, da sie keine wesentlichen Auswirkungen auf das Leben des Einzelnen haben). In Abbildung 1 haben wir diese Ereignisse in Form von farbigen Punkten gezeigt: erfolgreich in Grün und mit einem relativen Prozentsatz p _L und erfolglos in Rot und mit einem Prozentsatz ( 100 - p _L ). Die Gesamtzahl der Ereignispunkte N _E ist gleichmäßig verteilt, aber natürlich ist eine solche Verteilung nur für N _E → ∞ idealerweise gleichmäßig. In unseren Simulationen gibt es normalerweise N _E ≈ N / 2 , daher gibt es zu Beginn jeder Simulation eine zufällige signifikante Konzentration erfolgreicher oder erfolgloser Ereignispunkte in verschiedenen Regionen der Welt, während andere Regionen neutraler sind. Die nachfolgende zufällige Bewegung von Punkten innerhalb einer quadratischen Matrix, d. H. Der Welt, ändert nichts an diesem grundlegenden Merkmal des Modells, das eine unterschiedliche Anzahl von Erfolgs- oder Misserfolgsereignissen für verschiedene Menschen während ihres gesamten Lebens anzeigt, unabhängig von ihrem persönlichen Talent.


Abbildung 2: Normalverteilung des Talents in der Bevölkerung (wobei der Median m _T = 0,6 durch eine gestrichelte vertikale Linie und die Standardabweichung σ _T = 0,1 dargestellt sind - die Werte m _T ± σ _{T werden} als zwei gepunktete vertikale Linien angezeigt). Diese Verteilung wird im Intervall [0; 1] und ändert sich während der Simulation nicht.

Ein Simulationslauf untersucht eine Lebensdauer P von 40 Jahren (im Alter von 20 bis 60 Jahren) mit einem Zeitschritt δ _t von sechs Monaten. Zu Beginn der Simulation erhielten alle Agenten das gleiche Kapital C _i = C (0) Ɐ _i = 1, ..., N , was ihren anfänglichen Erfolg / ihr Wohlbefinden darstellt. Diese Wahl hat das offensichtliche Ziel, niemandem den anfänglichen Vorteil zu verschaffen. Während die Talente der Agenten nicht zeitabhängig sind, verändert sich ihr Kapital. Während der Entwicklung dieses Modells, d. H. Während des erwarteten Lebenszeitraums der Agenten, bewegen sich alle Ereignispunkte zufällig um die Welt und können sich gleichzeitig mit dem Standort einiger Agenten überschneiden. Wenn Sie auf Details eingehen, legt jeder Ereignispunkt jedes Mal in zufälliger Richtung die Entfernung von 2 Abschnitten zurück. Wir glauben, dass es einen Schnittpunkt mit dem Individuum gibt, wenn der innerhalb des Kreises mit einem Radius von einem Segment dargestellte Ereignispunkt auf dem Agenten zentriert ist (Ereignispunkte verschwinden nach dem Schnittpunkt nicht).Abhängig von einem solchen Vorfall sind zu diesem Zeitpunkt Schritt t (d. H. Alle sechs Monate) mit einem bestimmten Agenten A _k die folgenden drei möglichen Optionen möglich:

1. Kein Ereignispunkt kreuzt die Position von Agent A _k - dies bedeutet, dass in den letzten sechs Monaten keine derartigen Ereignisse aufgetreten sind und Agent A _k keine Aktion ausführt.
2. A _k – , ( , [30], , ); , A _k / , T _k . C _k (t) = 2C _k (t − 1) , rand[0; 1] < T _k , .., , .
3. A _k – , ; , A _k / , .. C _k (t) = C _k (t − 1) / 2 .

Die oben genannten Regeln für Agenten (einschließlich der Wahl, das Anfangskapital bei erfolglosen Ereignissen in zwei Hälften zu teilen und bei erfolgreichen Ereignissen im Verhältnis zum Talent des Agenten zu verdoppeln) sind absichtlich einfach und können als weit verbreitet angesehen werden, da sie auf der offensichtlichen Tatsache beruhen, dass Erfolg im täglichen Leben die Eigenschaft hat beide wachsen und sinken in rasantem Tempo. Darüber hinaus bieten diese Regeln hochtalentierten Menschen einen erheblichen Vorteil, da sie mehr von den Möglichkeiten des Glücks profitieren können (einschließlich der Fähigkeit, eine gute Idee zu verwenden, die aus ihrem Gehirn stammt). Andererseits sind beispielsweise ein Autounfall oder eine plötzliche Krankheit immer erfolglose Ereignisse, bei denen Talent keine Rolle spielt. In dieser Hinsicht können wir eine genauere Definition von "Talent" ableiten.Definieren Sie es als "jede persönliche Qualität, die die Chance erhöht, die Gelegenheit zu nutzen". Mit anderen Worten, unter dem Begriff „Talent“ verstehen wir im weiteren Sinne Intelligenz, Fähigkeiten, Einfallsreichtum, Hartnäckigkeit, Entschlossenheit, harte Arbeit, Risikobereitschaft und so weiter. Weiter werden wir sehen, dass der Vorteil eines großen Talents eine notwendige, aber nicht ausreichende Voraussetzung ist, um sehr hohe Erfolgsspitzen zu erreichen.

2.1. Ein Lauf ergibt

In diesem Unterabschnitt haben wir die Ergebnisse eines Laufs einer typischen Simulation vorgestellt. Im Allgemeinen sind diese Ergebnisse ziemlich stabil, daher können sie, wie wir unten zeigen, als wesentlich repräsentativ für den allgemeinen Rahmen angesehen werden, der unser Modell verlässt.

Stellen wir uns N = 1000 Agenten mit einer gleichen Menge Startkapital C (0) = 10 (in abstrakten Einheiten) und mit einem festen Talent T _i ϵ [0; 1] die folgende Normalverteilung mit einem Median m _T = 0,6 und einer Standardabweichung σ _T = 0,1 (siehe Abbildung 2). Wie bereits erwähnt, deckt die Simulation eine realistische Zeitspanne P ab= 40 Jahre, Entwicklung in gleichen Schritten, jeweils sechs Monate, insgesamt aus I = 80 Iterationen. In dieser Simulation haben wir N _E = 500 Ereignispunkte mit der Wahrscheinlichkeit erfolgreicher Ereignisse p _L = 50% genommen.

Wie aus Diagramm (a) in Abbildung 3 ersichtlich, haben wir am Ende der Simulation festgestellt, dass einfache dynamische Modellregeln eine ungleiche Verteilung von Kapital / Erfolg mit einer großen Anzahl armer (erfolgloser) Agenten und einer kleinen Anzahl extrem reicher (erfolgreicher) Agenten erzeugen können. Nachdem wir dieselbe Verteilung auf einer bilogarithmischen Skala konstruiert haben, sehen wir in Schema (b) derselben Figur die Verteilung gemäß der Potenzfunktion im Pareto-Stil, deren Steigung der Funktion y © ≈ C ^{−1.27 entspricht} .

Trotz der normalen Verteilung der Talente scheint das TPU-Modell in der Lage gewesen zu sein, das erste wichtige Merkmal zu erfassen, das im Vergleich zu realen Daten beobachtet wurde: die tiefste Kluft zwischen Arm und Reich und die unveränderliche Natur seiner Skala. Insbesondere erhielten in unserer Simulation nur 4 Personen mehr als 500 Kapitaleinheiten, und die 20 erfolgreichsten Personen besitzen 44% aller Werte, während fast die Hälfte der Bevölkerung weniger als 10 Einheiten hat. Im Allgemeinen wird die Pareto-Regel „80/20“ eingehalten, da 80% der Bevölkerung nur 20% des Gesamtkapitals besitzen, während die restlichen 20% der Personen 80% des Vermögens besitzen. Obwohl diese Ungleichheit zweifellos unfair erscheint, wäre es einigermaßen akzeptabel, wenn die meisten erfolgreichen Menschen zu den talentiertesten gehören würden.Dadurch verdienen Sie mehr Kapitalakkumulation / Erfolg als die anderen. Aber passiert das wirklich?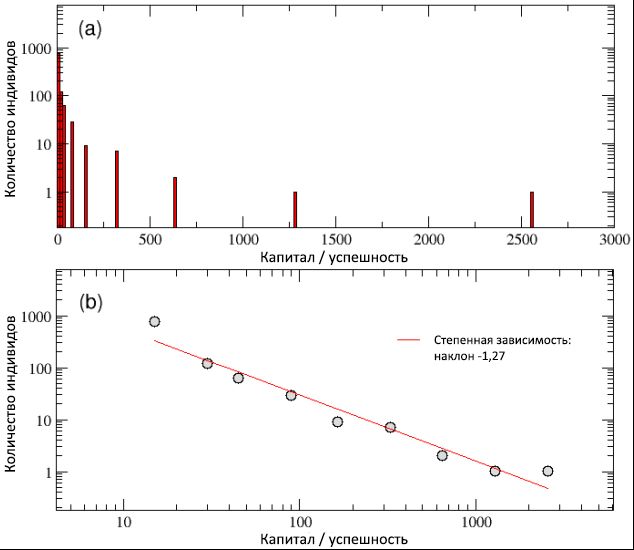


Abbildung 3: Die endgültige Verteilung von Wohlstand / Erfolg unter der Bevölkerung auf einer logarithmischen linearen (a) und bilogarithmischen (b) Skala. Trotz der normalen Talentverteilung kann das Ende der Erfolgsverteilung, wie aus Schema (b) ersichtlich, als Leistungskurve mit einer Steigung von –1,27 beschrieben werden. Wir haben auch bestätigt, dass die Verteilung von Kapital / Erfolg dem 80/20-Gesetz von Pareto folgt, da 20% der Bevölkerung 80% der Werte besitzen und umgekehrt.

In Fig. 4, Schemata (a) bzw. (b), wird Talent als Funktion des Gesamtkapitals / -erfolgs dargestellt und umgekehrt (beachten Sie, dass in Schema (a) Kapital / Erfolg nur diskrete Werte hat - dies hängt mit der Entscheidung zusammen Verwenden Sie für alle Agenten das gleiche Anfangskapital. Ein Blick auf beide Systeme zeigt, dass einerseits die erfolgreichsten Personen nicht die talentiertesten und umgekehrt die begabtesten Personen nicht die erfolgreichsten sind. Insbesondere das erfolgreichste Individuum mit C _max = 2560 hat das Talent T * = 0,61, das nur geringfügig über dem Medianwert m _T = 0,6 liegt, während das begabteste ( T _max= 0,89) hat eine Kapital- / Erfolgsrate von weniger als 1 Einheit ( C = 0,625).

Wie wir aus dem nächsten Unterabschnitt genauer erfahren, ist ein solches Ergebnis kein Sonderfall, sondern eine Regel für Systeme dieser Art: Maximaler Erfolg konvergiert nie mit maximalem Talent und umgekehrt. Darüber hinaus ist diese Diskrepanz zwischen Erfolg und Talent unverhältnismäßig und höchst nichtlinear. In der Tat, die durchschnittliche Kapital aller Menschen mit Talent T> T * eingestellt ist C≈ 20; Mit anderen Worten, das Kapital / der Erfolg der erfolgreichsten Menschen mit moderaten Talenten ist 128-mal höher als das durchschnittliche Kapital / der Erfolg der Menschen, die viel begabter sind als die ersten. Wir können daraus schließen, dass, wenn außergewöhnliches Talent nicht hinter dem Grund für den enormen Erfolg einiger Menschen verborgen ist, es vielleicht einen anderen Faktor gibt. Unsere Simulation zeigt deutlich, dass reines Glück ein solcher Faktor ist.


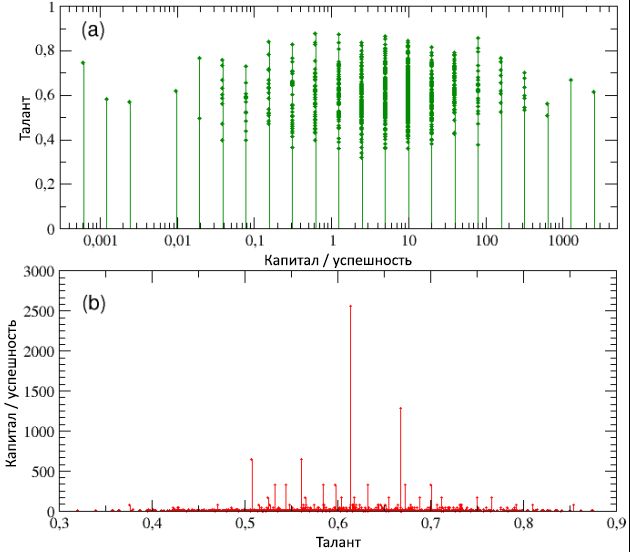Abbildung 4: In Diagramm (a) wird Talent als Funktion des Kapitals / Erfolgs dargestellt (logarithmisch zur besseren Visualisierung). Dies zeigt, dass die erfolgreichsten Personen nicht gleichzeitig die talentiertesten sind. In Diagramm (b) wird dagegen Kapital / Erfolg als Funktion des Talents dargestellt - hier können Sie besser beurteilen, dass der erfolgreichste Agent mit C _max= 2560, hat ein Talent, das den Medianwert m _T = 0,6 nur geringfügig überschreitet , während der begabteste ein Kapital / Erfolg von weniger als C = 1 Einheit hat, viel weniger als das Anfangskapital C (0). Lesen Sie weiter für weitere Details.

In Abbildung 5 ist die Anzahl der erfolgreichen und erfolglosen Ereignisse, die bei allen Menschen während ihres Arbeitslebens aufgetreten sind, als Funktion ihres Gesamtkapitals / Erfolgs dargestellt. Bei der Betrachtung von Schema (a) wird deutlich, dass die erfolgreichsten Personen gleichzeitig die erfolgreichsten sind (beachten Sie, dass dieses Diagramm alle erfolgreichen Ereignisse zeigt, die den Agenten passiert sind, und nicht nur diejenigen, von denen sie entsprechend profitieren konnten mit deinem Talent). Im Gegenteil, wenn wir Schema (b) betrachten, sehen wir, dass die gleichzeitig erfolglosesten die erfolglosesten sind. Mit anderen Worten, obwohl es auf der Grundlage von Simulationen keine Korrelation zwischen Erfolg und Talent gibt, besteht eine starke Abhängigkeit des Erfolgs vom Glück. Wir analysierten die Details der Häufigkeitsverteilungen der Anzahl erfolgreicher und erfolgloser Ereignisse, die bei Einzelpersonen auftratenWie in den Diagrammen © und (d) gezeigt, sind diese beiden Werte exponentiell mit Graden von 0,64 und 0,48 und Medianwerten von 1,35 bzw. 1,66, und die maximale Anzahl erfolgreicher und erfolgloser Ereignisse ist aufgetreten. 10 und 15. Darüber hinaus hatten ungefähr 16% ein „neutrales“ Leben, im Allgemeinen ohne erfolgreiche und erfolglose Ereignisse, während 40% der Personen ausschließlich einer Art von Ereignis begegneten (erfolgreich oder erfolglos).während 40% der Personen nur auf eine Art von Ereignis stießen (erfolgreich oder erfolglos).während 40% der Personen nur auf eine Art von Ereignis stießen (erfolgreich oder erfolglos).

Es ist auch interessant, die Entwicklungsphase von Erfolg / Kapital sowohl für die erfolgreichsten als auch für die erfolglosesten Personen im Vergleich zu den entsprechenden Sequenzen erfolgreicher und erfolgloser Ereignisse zu betrachten, die über 40 Jahre (80 Intervalle, jeweils 6 Monate) ihres Arbeitslebens aufgetreten sind. Die Ergebnisse sind jeweils im linken und rechten Teil von 6 zu sehen. Im Gegensatz zu Schema (a) aus Bild 5 enthalten die unteren Schemata dieser Figur nur die erfolgreichen Ereignisse, von denen Agenten aufgrund ihres Talents profitieren konnten.


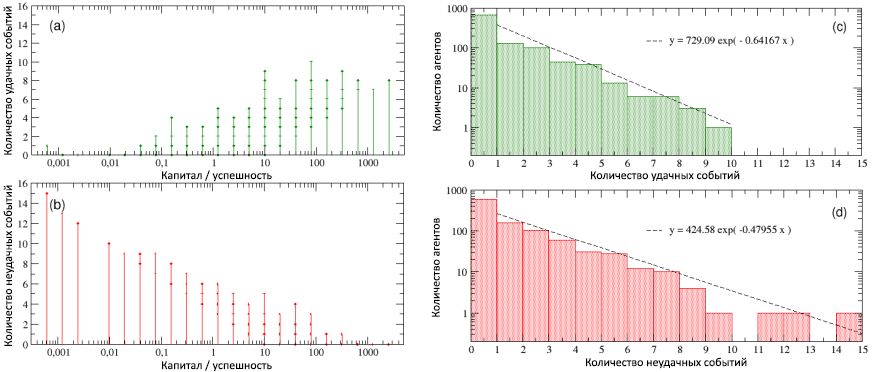Abbildung 5: Gesamtzahl der erfolgreichen (a) und erfolglosen (b) Ereignisse als Funktionen des Kapital- / Agentenerfolgs. Die Grafik zeigt eine starke Korrelation zwischen Erfolg und Erfolg: Die erfolgreichsten Personen sind auch die erfolgreichsten und umgekehrt. Aufgrund der Verwendung des gleichen Anfangskapitals für alle Agenten stellt sich erneut heraus, dass eine Reihe von Ereignissen in diskreten Werten für Kapital / Erfolg zusammengefasst sind. In den Diagrammen © und (d) wird die Häufigkeit der Verteilungen der Anzahl erfolgreicher und nicht erfolgreicher Ereignisse auf einer logarithmisch linearen Skala angezeigt. Wie zu sehen ist, können beide Verteilungen in Form von Exponentialabhängigkeiten mit ähnlichen negativen Potenzen geschrieben werden.

In den (oberen und unteren) Diagrammen (a) von 6, die einen mäßig talentierten, aber erfolgreichsten Menschen betreffen, ist deutlich zu sehen, dass nach etwa der Hälfte seines Arbeitslebens eine seltene Manifestation erfolgreicher Ereignisse (unteres Diagramm) und ein niedriges Kapitalniveau (oberes) auftreten Schema) führte die plötzliche Konzentration günstiger Ereignisse zwischen 30 und 40 Zeitschritten (d. h. kurz vor dem 40. Geburtstag des Agenten) zu einer raschen Kapitalerhöhung, die in den letzten 10 Schritten (d. h. in den letzten 5 Jahren der Karriere des Agenten) erfolgte ) wurde exponentiell, indem man von C ging = 320 bis C _max = 2560.

Auf der anderen Seite wird bei Betrachtung der (oberen und unteren) Diagramme (b) derselben Figur in Bezug auf die am wenigsten erfolgreiche Person deutlich, dass eine besonders erfolglose zweite Hälfte ihres Arbeitslebens, begleitet von einem Dutzend unerwünschter Ereignisse, das Kapital / den Erfolg ständig reduzierte und zum Finale führte Wert C = 0,00061. Es ist interessant festzustellen, dass das Talent dieses unglücklichen Agenten T war= 0,74, was höher ist als die meisten der erfolgreichsten. Offensichtlich wurde die Schaffung des Unterschieds durch das Glück beeinflusst. Und wenn es stimmt, dass der erfolgreichste Agent es verdient hat, von allen ihm gebotenen Möglichkeiten zu profitieren (trotz seines mittelmäßigen Talents), ist es auch wahr, dass wenn Ihr Leben voller Unglück ist und keine Chancen bietet, wie dieser zweite Agent, dann sogar Das größte Talent wird gegen gewaltsames Versagen machtlos.


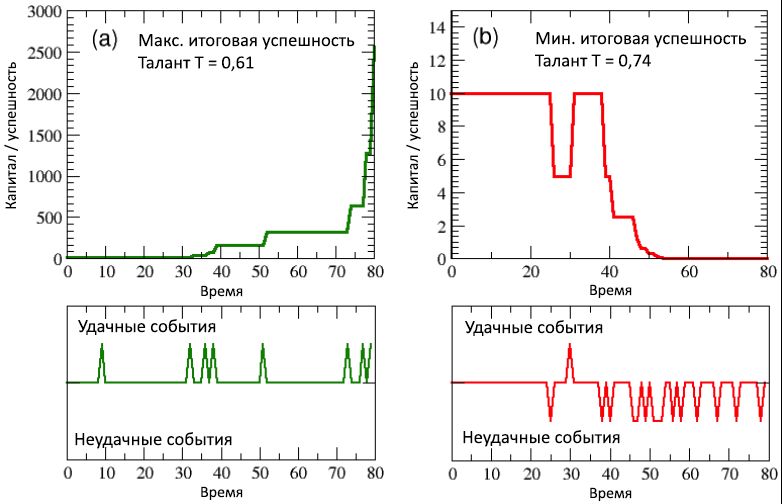Fig. 6: (a) die Entwicklungsperiode des Erfolgs / Kapitals des erfolgreichsten Individuums und (b) des unglücklichsten, verglichen mit den entsprechenden Sequenzen erfolgreicher und erfolgloser Ereignisse, die während ihres Arbeitslebens auftraten (von 80 halben Jahren, d. H. 40 Jahren). Der Zeitpunkt des Auftretens solcher Ereignisse ist in den unteren Diagrammen in Form von aufsteigenden und absteigenden Spitzen angegeben.

Alle in diesem Unterabschnitt vorgestellten Ergebnisse eines einzelnen Laufs (die für diese Simulation verwendete Demoversion des NetLogo-Codes des TPU-Modells befindet sich im Open ABM- Repository ) sind sehr stabil und werden, wie wir im nächsten Unterabschnitt sehen werden, mit geringfügigen Unterschieden mit gespeichert Viele Wiederholungen von Simulationen beginnen mit der gleichen Talentverteilung, aber mit unterschiedlichen zufälligen Positionen von Individuen.

2.2. Mehrere Laufergebnisse

In diesem Unterabschnitt haben wir die allgemeinen Simulationsergebnisse von durchschnittlich mehr als 100 Läufen vorgestellt, die jeweils mit unterschiedlichen, zufällig ausgewählten Anfangsbedingungen gestartet wurden. Die Werte der Kontrollparameter waren die gleichen wie im vorherigen Unterabschnitt: N = 1000 Individuen, m _T = 0,6 und σ _T = 0,1 für die Normalverteilung des Talents, I = 80 Iterationen (jede repräsentiert δ _t = 6 Monate Arbeitsleben ), C (0) = 10 Einheiten des Anfangskapitals, N _E = 500 Ereignispunkte und der Prozentsatz erfolgreicher Ereignisse p _L = 50%.

In Diagramm (a) von 7 ist die Gesamtverteilung des Gesamtkapitals / -erfolgs unter allen als Ergebnis von 100 Läufen gesammelten Agenten auf einer logarithmischen Skala gezeigt und wird durch eine Potenzgesetzkurve mit einem Winkelkoeffizienten –1,33 gut beschrieben. Die Eigenschaft der Kapitalkonstanz, die in einem einzigen Lauf unabhängig von der Größe beobachtet wird, und die daraus resultierende hohe Ungleichheit zwischen Individuen sowie die Pareto-Regel „80/20“ bleiben somit bei mehreren Läufen erhalten. Tatsächlich hat sich die Kluft zwischen reichen (erfolgreichen) und armen (erfolglosen) Agenten sogar vergrößert, da die Hauptstadt der reichsten Menschen inzwischen 40.000 Einheiten überschritten hat.

Dieses Ergebnis lässt sich am besten anhand des Schemas (b) in Abbildung 7 abschätzen, in dem das Gesamtkapital C _max nur der erfolgreichsten Personen als Funktion des Talents angegeben ist zeigt das beste Ergebnis in jedem der 100 Läufe. Der Agent mit dem Talent T _best = 0,6048, der fast mit dem Median der Talentverteilung ( m _T = 0,6) übereinstimmt und das Spitzenkapital C _best = 40960 erreichte, erhielt die meisten Punkte. Auf der anderen Seite der begabteste der erfolgreichsten Personen mit Talent T _max = 0,91, gewonnenes Kapital C _max = 2560, was nur 6% von C am _{besten ist} .


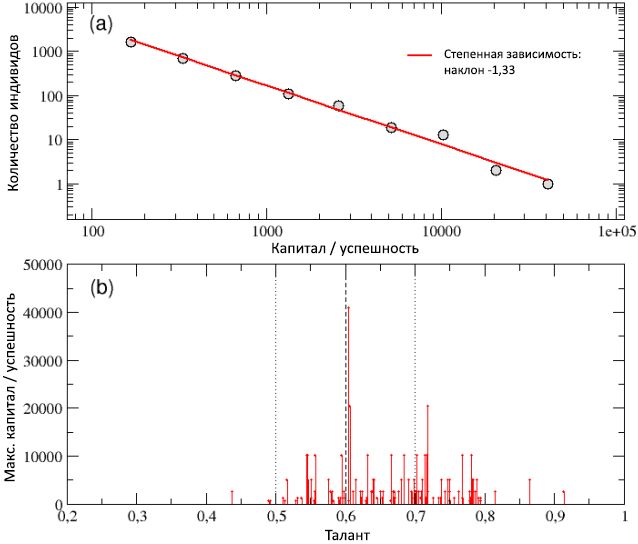
Abbildung 7: Schema (a) - Verteilung des Gesamtkapitals / -erfolgs, berechnet über 100 Läufe für Populationen mit unterschiedlichen zufällig bestimmten Anfangsbedingungen. Die Verteilung kann durch eine Leistungskurve mit einer Steigung von -1,33 beschrieben werden. Schema (b) - das Gesamtkapital C _{max der} erfolgreichsten Personen in jedem der 100 Läufe, angezeigt als Funktion ihres Talents. Menschen mit mäßig hohem Talent sind im Durchschnitt erfolgreicher als Menschen mit geringem oder mäßig niedrigem Talent, und meistens ist die erfolgreichste Person ein mäßig begabter Agent und nur gelegentlich der talentierteste. Der Wert von m _T sowie die Werte von m _T ± σ _T sind jeweils in Form von vertikalen gestrichelten und gepunkteten Linien gezeigt.

Um diesen Gesichtspunkt genauer zu betrachten, haben wir in Abbildung 8 (a) die Talentverteilung der besten Leistungsträger aufgetragen, berechnet für 100 Läufe. Die Verteilung ist offensichtlich entlang der Talentachse mit einem Durchschnittswert von T _av = 0,66> m _T nach rechts verschoben - dies bestätigt einerseits, dass zum Erreichen eines signifikanten Erfolgs häufig ein mäßig hohes Talent erforderlich ist; Andererseits zeigt es auch, dass diese Bedingung fast nie genug ist, da Agenten mit dem höchsten Talent (d. h. mit T > m _T = 2 & sgr; _T oder T > 0,8) nur zu den besten Leistungsträgern gehören in 3% der Fälle und ihr Kapital / Erfolg überschreitet nie 13% von C am _besten .


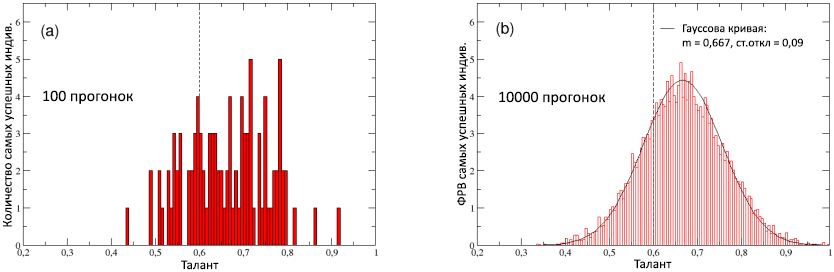
Abbildung 8: (a) Talentverteilung der erfolgreichsten Persönlichkeiten (besten Darsteller) in jedem der 100 Läufe. (b) Die Wahrscheinlichkeitsverteilungsfunktion (RFF) des Talents der erfolgreichsten Personen, berechnet in 10.000 Läufen: wird durch die Normalverteilung mit einem Median von 0,667 und einer Standardabweichung von 0,09 (durchgezogene Kurve) gut beschrieben. Zum Vergleich ist der Median m _T = 0,6 der anfänglichen Normalverteilung des Talents in der Bevölkerung gezeigt, der in beiden Schemata durch eine gestrichelte vertikale Linie dargestellt ist.

In Diagramm (b) von 8 wird dieselbe Verteilung (reduziert auf die Gesamtfläche, um die FRF zu erhalten) für 10.000 Läufe berechnet, um ihre wahre Form zu verstehen: Es sieht so aus, als würde sie in eine Gaußsche Kurve G (T) mit einem durchschnittlichen T _av = 0,667 passen und eine Standardabweichung von 0,09 (durchgezogene Linie). Dies bestätigt natürlich, dass die Talentverteilung der besten Leistungsträger im Vergleich zur ursprünglichen Talentverteilung relativ zur Talentachse nach rechts verschoben ist. Genauer gesagt bedeutet dies, dass die bedingte Wahrscheinlichkeit P ( C _max | T ) = G (T) dT ist, unter den besten Darstellern eine Persönlichkeit mit Talent im Intervall [ T ; T + dT ] wächst mit dem Talent T , erreicht Spitzenwerte nahe dem mittleren bis mittleren Talent T _av = 0,66 und fällt dann mit großen Talentwerten stark ab. Mit anderen Worten, die Wahrscheinlichkeit, zusätzlich zum Erfolg eine mäßig talentierte Person zu finden, ist höher als die Wahrscheinlichkeit, dort eine hochbegabte Person zu finden. Beachten Sie, dass in einer idealen Welt, in der Talent der Hauptgrund für den Erfolg war, erwartet wird, dass P ( C _max | T ) eine wachsende Funktion von T sein wird. Wir können daher den Schluss ziehen, dass die beobachtete Gaußsche Form P ( C _max | T ) ein Beweis dafür ist, dass Glück eine größere Bedeutung hat als Talent, um ein extrem hohes Erfolgsniveau zu erreichen.


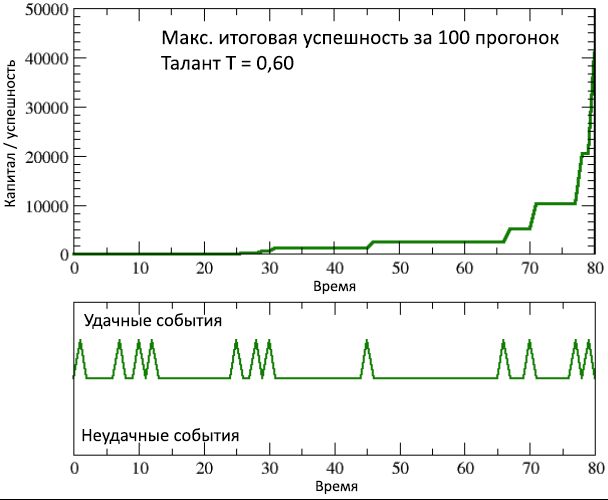
Abbildung 9: Änderung der Erfolgszeit / des Kapitals der erfolgreichsten Person (aber gleichzeitig mäßig begabt) aus 100 Simulationsläufen im Vergleich zu der entsprechenden ungewöhnlichen Abfolge erfolgreicher Ereignisse in ihrem Leben.

Es ist auch interessant, aus 100 Läufen die durchschnittliche Kapital- / Erfolgsrate C _mt ≈ 63 der talentiertesten Personen mit dem entsprechenden durchschnittlichen C _bei ≈ 33 derjenigen zu vergleichen, deren Talent nahe am Median m _{T liegt.} In beiden Fällen fanden wir eher niedrige Indikatoren (auch wenn mehr als das Anfangskapital C (0) = 10), aber die Tatsache, dass C _mt > C _at anzeigt, zeigt, dass die Wahrscheinlichkeit, eine mäßig talentierte Person an der Spitze des Erfolgs zu finden, zwar höher ist, Im Vergleich zu denjenigen, die hochbegabt sind, sind die talentiertesten Personen jedes Laufs im Durchschnitt erfolgreicher als mäßig begabte Personen. Betrachtet man dagegen den Durchschnitt von über 100 Läufen, so berechnet sich der Anteil der Personen mit Talent T > 0,7 (d. H. Höher als mit einer Standardabweichung vom Median) und dem endgültigen Erfolg / Kapital C- _Ende > 10 unter Berücksichtigung aller Agenten mit Talent T > 0,7 (davon durchschnittlich für jeden Lauf ≈ 160), wir haben festgestellt, dass dieser Anteil 32% beträgt - dies bedeutet, dass die kombinierte Leistung der talentiertesten Menschen in unserer Bevölkerung im Durchschnitt relativ gering ist, da nur Ein Drittel von ihnen erreicht ein Gesamtkapital, das über dem Original liegt.

In jedem Fall ist die Tatsache, dass der beste Darsteller unter den 100 Simulationsläufen ein Agent mit dem Talent T _best = 0,6 ist, das perfekt zum Median passt, und mit dem Enderfolg C _best = 40960, der 650-mal höher als C _mt ist, _{unwiderlegbar} . und mehr als 4.000 Mal höher als der Erfolg von C _end <10 bei 2/3 der talentiertesten Leute. Dies geschah am Ende einfach, weil er mehr Glück hatte als die anderen. Bedingungsloses Glück, wie aus Abbildung 9 ersichtlich ist, die das Wachstum seines Kapitals / Erfolgs im Laufe seines Arbeitslebens zeigt, zusammen mit einer beeindruckenden Reihe erfolgreicher (und nur erfolgreicher) Veranstaltungen, von denen er trotz des Mangels an außergewöhnlichem Talent während seiner Zeit profitieren konnte Karrieren.

Zusammenfassend wurde an dieser Stelle festgestellt, dass das TPU-Modell trotz seiner Einfachheit in der Lage zu sein scheint, viele Merkmale zu berücksichtigen, die, wie in der Einleitung erwähnt, die hohe Ungleichheit in der Verteilung von Wohlstand und Erfolg in unserer Gesellschaft charakterisieren, die eindeutig im Gegensatz zur Gaußschen Verteilung von Talenten unter steht Menschen. Das Modell in quantitativer Form zeigt auch, dass großes Talent für eine garantierte erfolgreiche Karriere nicht ausreicht und dass im Gegenteil weniger begabte Menschen sehr oft den Höhepunkt des Erfolgs erreichen - dies ist eine weitere „bedingte Tatsache“, die im wirklichen Leben häufig beobachtet wird [35, 36, 38].

Ein Schlüsselaspekt, der intuitiv erklärt, wie es passieren kann, dass mäßig begabte Menschen (so oft) viel mehr Ehre und Erfolg erzielen als talentiertere, ist, dass es eine versteckte und oft unterschätzte Rolle des Glücks gibt, wie es klar ist aus unseren Simulationen gesehen. Um die wahre Bedeutung der Ergebnisse unserer Forschung zu verstehen, ist es wichtig, zwischen Makro- und Mikrogesichtspunkten zu unterscheiden.

Tatsächlich ist es auf Mikroebene nach den dynamischen Regeln des TPU-Modells von vornherein wahrscheinlicher, dass ein begabter Mensch ein hohes Maß an Erfolg erzielt als ein mäßig talentierter, da er die Gelegenheit besser nutzen kann. Aus der Sicht eines Individuums sollten wir daher zu dem Schluss kommen, dass die beste Strategie zur Erhöhung der Erfolgswahrscheinlichkeit (auf jeder Ebene des Talents) darin besteht, die persönliche Aktivität zu erhöhen, Ideen zu generieren und zu kommunizieren, da (per Definition) das Auftreten erfolgreicher Ereignisse nicht beeinflusst werden kann mit anderen Menschen die Suche nach Vielfalt und gegenseitiger Bereicherung. Mit anderen Worten, wenn Sie eine aufgeschlossene Person werden, die bereit ist, mit anderen in Kontakt zu treten, besteht die höchste Wahrscheinlichkeit für eine erfolgreiche Veranstaltung (die im Ausmaß des individuellen Talents realisiert wird).

Andererseits ist auf Makroebene aus Sicht der gesamten Gesellschaft die Wahrscheinlichkeit, mäßig begabte Personen an der Spitze des Erfolgs zu treffen, viel höher als bei der Suche nach äußerst talentierten Menschen, da die ersteren viel größer sind und dank des Glücks im Allgemeinen viel mehr haben der Vorteil eines enormen Erfolgs, trotz ihrer a priori geringeren persönlichen Wahrscheinlichkeit.

Im nächsten Abschnitt werden wir diesen Standpunkt auf Makroebene betrachten und die Möglichkeiten unseres Modells untersuchen, um effektivere Strategien und Strategien zur Verbesserung des durchschnittlichen Leistungsniveaus der talentiertesten Menschen in der Bevölkerung genauer zu untersuchen und produktivere Methoden zur Verteilung von Belohnungen und Ressourcen zu implementieren. Tatsächlich erwarten wir, dass jede Politik, die das Niveau der talentiertesten Personen erhöhen kann, die der Motor für Fortschritt und Innovation in unserer Gesellschaft sind, eine kumulative positive Wirkung hat.

3. Effektive Strategien zum Ausgleich des Glücks

Die im vorherigen Abschnitt vorgestellten Ergebnisse stimmen eindeutig mit den in der Einleitung dokumentierten empirischen Beweisen überein, die die meritokratische Annahme in Frage stellen, dass die natürlichen Unterschiede in Bezug auf Talent, Fähigkeiten, Fähigkeiten, Intelligenz, harte Arbeit oder Ausdauer die einzigen Gründe für den Erfolg sind. Wie wir gezeigt haben, hat Glück auch Auswirkungen und kann eine entscheidende Rolle spielen. Der Kern der Diskussion besteht darin, dass aufgrund der schwierigen Messbarkeit (in vielen Fällen ist es schwierig, sie genau zu bestimmen) persönlicher Qualitäten häufig meritokratische Strategien verwendet werden, um Ehrungen, Finanzierungen oder Auszeichnungen zu verteilen, die häufig auf privaten Ergebnissen beruhen und an persönlichem Wohlstand oder Erfolg gemessen werden. Infolgedessen beeinflussen solche Strategien die weiteren Maßnahmen zur Stärkung und Steigerung des Wohlstands / Erfolgs der erfolgreichsten Personen aufgrund des positiven Rückkopplungsmechanismus, der dem Prozess „Reich wird reich“ (auch als „Matthew-Effekt“ bekannt) ähnlich ist [57, 58, 59]. mit einem unfairen Ergebnis.

Stellen wir uns zum Beispiel einen staatlich finanzierten Forschungs- und Entwicklungsrat vor, dem ein fester Geldbetrag zur Verfügung steht. Was wird viel effektiver sein, um die durchschnittliche Forschungseffektivität zu steigern: nur wenigen zweifellos hervorragenden Wissenschaftlern große Zuschüsse zu gewähren oder vielen offensichtlich gewöhnlicheren Wissenschaftlern kleine Zuschüsse zu gewähren? Eine kürzlich durchgeführte Studie [44], die auf einer Analyse von vier Indizes zur wissenschaftlichen Bedeutung verwandter Veröffentlichungen basiert, ergab, dass die Bedeutung nur eine schwache positive Beziehung zur Finanzierung hat. Insbesondere war die Bedeutung des Dollars für große Stipendiaten geringer, und die Bedeutung von Wissenschaftlern, die eine Aufstockung der Mittel erhielten, nahm nicht in angemessenem Maße zu. Die Autoren der Studie kamen zu dem Schluss, dass die wissenschaftliche Bedeutung (wie in der Veröffentlichung dargestellt) nur schwach an die Finanzierung grenzt, und schlugen vor, dass Finanzierungsstrategien, die eher auf die Diversifizierung von Ideen als auf „Exzellenz“ abzielen, wahrscheinlich produktiver sind. Ein späterer Beitrag [60] zeigte, dass sowohl in Bezug auf die Anzahl der erstellten Dokumente als auch in Bezug auf ihre wissenschaftliche Bedeutung eine konzentrierte Forschungsfinanzierung in der Regel zu sinkenden Grenzerträgen führt und dass die am meisten finanzierten Forscher nicht in Bezug auf Leistung und wissenschaftliche Bedeutung hervorstechen. Im Allgemeinen sollten solche Schlussfolgerungen angesichts einer anderen jüngsten Entdeckung [18] nicht überraschend sein, wonach die Bedeutung, gemessen an einflussreichen Veröffentlichungen, zufällig auf eine Reihe von Veröffentlichungen des Wissenschaftlers verteilt ist. Mit anderen Worten, Glück ist wichtig, und wenn es mehr betrifft, als wir zugeben wollen, ist es nicht verwunderlich, dass meritokratische Strategien weniger effektiv sind als erwartet, insbesondere wenn wir versuchen, das Verdienst eines Posteriori zu würdigen. In früheren Studien [48, 49, 50, 51, 52, 53, 54, 55] wurde bereits vor dieser Art von „Near Meritocracy“ gewarnt, was die Wirksamkeit alternativer Strategien auf der Grundlage von Zufallswahlen in den Bereichen Management, Politik und Finanzen zeigt. Unter diesem Gesichtspunkt zeigt das TPU-Modell, wie das Mindestmaß an Erfolg für die meisten talentierten Menschen auf der Welt gesteigert werden kann, wo Glück wichtig ist und zufällige Entdeckungen häufig zu wichtigen Erfolgen führen.

3.1. Versehentliche Entdeckung, Innovation und effektive Finanzierungsstrategien

Der Begriff „zufällige Entdeckung“ wird häufig in literarischen Verweisen auf historische Fakten verwendet, was zeigt, dass Forscher häufig unerwartete und nützliche Entdeckungen rein zufällig machen, wenn sie nach etwas anderem suchen [61, 62]. Es gibt eine lange Liste von Entdeckungsgeschichten, die ausschließlich zufällig gemacht wurden: vom Penicillin von Alexander Fleming bis zur Radioaktivität von Marie Curie, von der kosmischen Mikrowellen-Hintergrundstrahlung der Radioastronomen Arno Penzias und Robert Woodrow Wilson bis zum Graphen Andrei Geim und Konstantin Novosyolov. Hier ein neueres Beispiel: Ein Netzwerk von mit Flüssigkeit gefüllten Kanälen im menschlichen Körper, einem bisher unbekannten Organ, das offenbar die Ausbreitung von Krebszellen fördert, wurde zufällig während einer einfachen Endoskopie entdeckt [63]. Daher denken viele Menschen, dass neugierige Forschung immer finanziert werden sollte, da niemand wirklich im Voraus wissen oder vorhersagen kann, wozu sie führen [64].

Ist es möglich, die Bedeutung der zufälligen Entdeckung zu quantifizieren? Was sind die effektivsten Methoden, um zufällige Entdeckungen zu simulieren? Es kann viele verschiedene Formen annehmen und es ist schwierig zu begrenzen und zu quantifizieren. Aus diesem Grund haben akademische Studien bisher eine zufällige wissenschaftliche Entdeckung größtenteils als philosophisches Konzept betrachtet. Aber die Zeiten ändern sich. Der Europäische Forschungsrat hat dem Biochemiker Ohid Yakubu kürzlich einen Zuschuss in Höhe von 1,7 Mio. USD gewährt, um die Bedeutung einer zufälligen Entdeckung in der Wissenschaft zu berechnen [65]. Yakub fand heraus, dass zufällige Entdeckungen in vier Grundtypen eingeteilt werden können [66] und dass es wichtige Faktoren geben kann, die das Erscheinungsbild beeinflussen. Seine Ergebnisse scheinen mit Ideen aus früheren Forschungen übereinzustimmen [67, 68, 69, 70, 71, 72], die argumentieren, dass allgemein akzeptierte, eindeutig meritokratische Strategien, die Überlegenheit anstreben und Vielfalt ersetzen, dazu bestimmt sind, zu verlieren und unwirksam. Der Grund dafür ist, dass sie a priori Forschungen ablehnen, die anfangs weniger vielversprechend aussahen, die aber insbesondere dank einer zufälligen Entdeckung a posteriori unglaublich innovativ sein könnten.

Unter diesem Gesichtspunkt wollen wir das TPU-Modell anwenden, das natürlich Glück (und folglich zufällige Entdeckung) als quantitativen Parameter der Strategie ausdrückt, um die Wirksamkeit verschiedener Finanzierungsszenarien in diesem Unterabschnitt zu untersuchen. Insbesondere in Situationen, in denen, wie oben erwähnt, eine mäßig talentierte, aber glückliche Person häufig erfolgreicher ist als begabte, aber unglückliche Personen, ist es wichtig, die Wirksamkeit von Finanzierungsstrategien zu bewerten, um ein Mindestmaß an Erfolg aufrechtzuerhalten, einschließlich z die talentiertesten Leute, von denen erwartet wird, dass sie die innovativsten und fortschrittlichsten Ideen einbringen.

Beginnend mit den gleichen Anfangsparametern, die in Unterabschnitt 2.2 verwendet wurden, d.h. N = 1000, m _T = 0,6, σ _T = 0,1, I = 80, δ _t = 6, C (0) = 10, NE = 500, p _L = 50% und 100 Simulationsläufe, stellen wir uns vor dass das verfügbare Gesamtfinanzierungskapital F _T nach verschiedenen Kriterien regelmäßig auf den Einzelnen verteilt wird. Zum Beispiel können Finanzen ausgegeben werden:

1. Gleichermaßen geteilt (egalitäre Kriterien) zur Förderung der Forschungsvielfalt;
2. Nur ein bestimmter Prozentsatz der erfolgreichsten („besten“) Personen (elitäres Kriterium), das zuvor als „nahe“ Meritokratie bezeichnet wurde, für die Verteilung der Finanzen unter den Menschen auf der Grundlage der Leistung in der Vergangenheit.
3. "Premium" -Verteilung unter einem bestimmten Anteil der erfolgreichsten Personen und der Rest zu kleinen gleichen Teilen über den Rest (gemischtes Kriterium);
4. Nur ein bestimmter Prozentsatz der zufällig ausgewählten Personen (zufälliges Zufallskriterium).

Wir gehen realistisch davon aus, dass das Gesamtkapital F _T während des 40-jährigen Zeitraums jedes Simulationslaufs alle 5 Jahre zugewiesen wird, so dass von Zeit zu Zeit F _T = 8 Kapitaleinheiten verteilt werden . Durch regelmäßige Injektionen dieser Finanzen wollen wir ein Mindestmaß an Ressourcen der talentiertesten Agenten aufrechterhalten. Ein guter Indikator für die Wirksamkeit der gewählten Finanzierungsstrategie kann daher der Prozentsatz P _{T sein} , der für 100 Simulationsläufe durchschnittlich ist, für Personen mit Talent T > m _T + σ _T , deren Gesamterfolg / Kapital das Anfangsniveau, d. H. C- _Ende, überschreitet> C (0).

Dieser Prozentsatz wurde bereits während der in Unterabschnitt 2.2 dargestellten Simulationsläufe berechnet. Es zeigt, dass ohne die Finanzierung die beste Leistung von den erfolgreichsten Agenten mit nahezu durchschnittlichem Talent erzielt wurde, während das Kapital / der Erfolg der talentiertesten Leute immer extrem niedrig bleibt. Insbesondere konnte nur ein Teil von P _T0 ≈ 32% der Gesamtzahl der Agenten mit Talent T > 0,7 basierend auf den Ergebnissen der Simulation ein Kapital / Erfolg erzielen, das den Anfangswert überstieg. Um die Wirksamkeit verschiedener Finanzierungsstrategien zu vergleichen, sollte daher das Wachstum des durchschnittlichen Prozentsatzes P _T relativ zu P _T0 berechnet werdenjene talentierten Leute, die ihr Anfangskapital während ihrer Karriere erhöht haben. Definieren wir dieses Wachstum als P ^* _T = P _T - P _T0 . Dieser Wert ist ein ziemlich stabiler Indikator: Wir haben ihn durch Wiederholung von 100 Simulationen überprüft. Die Streuung der P ^* _T- Werte blieb unter 2%. Wenn wir schließlich das Verhältnis von P ^* _T zum Gesamtkapital berechnen, das über 40 Jahre auf alle Agenten verteilt ist, können wir einen Effizienzindex E erhalten , der das Wachstum der Anzahl ausreichend erfolgreicher Talente pro Einheit des investierten Kapitals misst, definiert als E = P ^* _T./ Die F _T .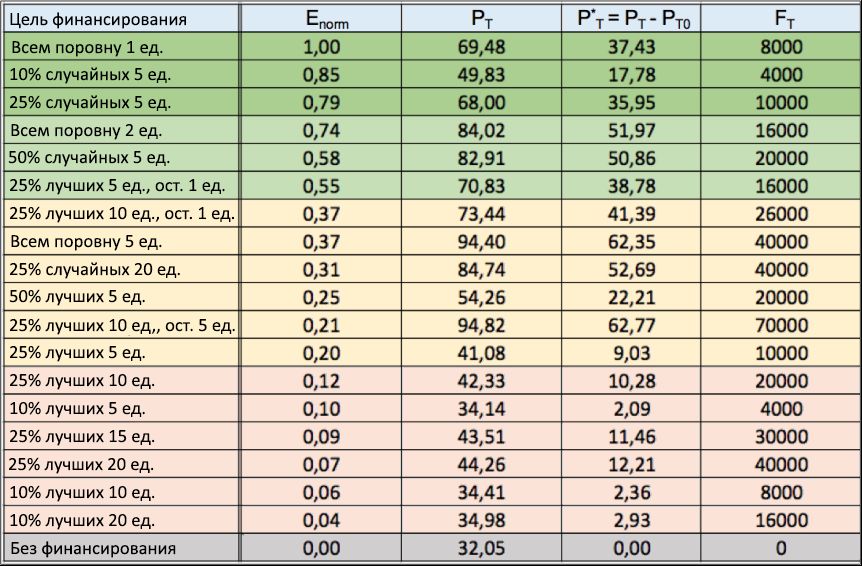


Abbildung 10: Tabelle der Finanzierungsstrategien. Es werden verschiedene Strategien zur Verteilung der Finanzen für verschiedene Zwecke (1 Spalte) mit den Ergebnissen der _Norm des normalisierten Effizienzindex E (2 Spalten) in absteigender Reihenfolge vorgestellt. In der dritten bzw. vierten Spalte werden die Werte des Anteils P _T erfolgreicher Talente und die Nettoerhöhung ihrer Anzahl P ^* _T in Bezug auf das Szenario „ohne Finanzierung“ im Durchschnitt für 100 Simulationsläufe angezeigt . Schließlich zeigt die letzte Spalte das Gesamtkapital F _T , das in jeden Lauf investiert wurde.

In der in Abbildung 10 gezeigten Tabelle haben wir den Leistungsindex (2. Spalte) gezeigt, der für mehrere Finanzierungsverteilungsstrategien mit jeweils eigenem finanziellen Zweck (1 Spalte) erhalten wurde, sowie die entsprechenden Werte von P _T (3. Spalte) und P. ^* _T (4. Spalte). In derselben Spalte, in der letzten Spalte, wird das insgesamt investierte Kapital F _T für jeden Lauf angegeben . Der Wirkungsgradindex E wurde relativ zu seinem Maximalwert E _max normalisiert , und alle Datensätze (Zeilen) sind nach dem Kriterium abnehmender Werte von E _norm = E / E _max geordnet. Für das Szenario mit fehlender Finanzierung ist per Definition E- _Norm = 0. Die gleichen Ergebnisse der E- _Norm sind in Abhängigkeit von den angenommenen Finanzierungsstrategien in Form eines Histogramms in Abbildung 11 dargestellt. Aufgrund der statistischen Stabilität P _T mit Abweichungen von weniger als 2% ergeben sich die angegebenen Ergebnisse des Effizienzindex E. _Norm sind stabil.

Wenn man die obige Tabelle und das entsprechende Histogramm aus Abbildung 11 betrachtet, wird deutlich, dass es viel besser ist, allen Personen gleichzeitig (sogar einen kleinen) Kapitalbetrag zuzuweisen, wenn das Ziel darin besteht, die talentiertesten Personen zu belohnen (wodurch ihr endgültiger Erfolg gesteigert wird). anstatt nur einem kleinen Teil von ihnen mehr Kapital auszugeben, das nach dem zum Zeitpunkt der Verteilung erzielten Erfolg ausgewählt wird.


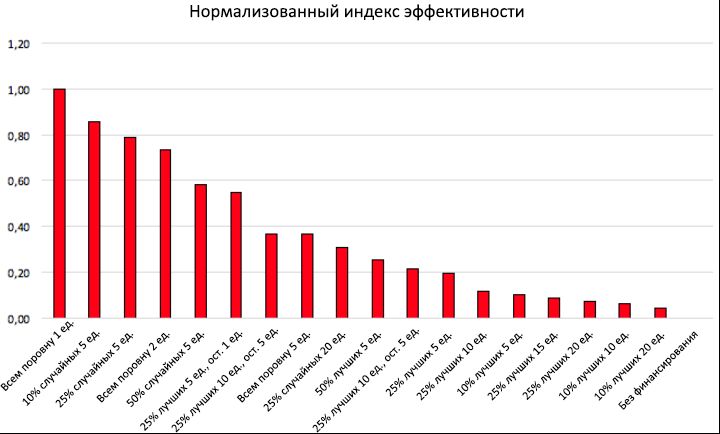Abbildung 11: Normalisierter Leistungsindex einiger Finanzierungsstrategien. Die Werte der _Norm des normalisierten Effizienzindex E werden in Abhängigkeit von verschiedenen Finanzierungsstrategien angegeben. Die Abbildung zeigt, dass, um den Erfolg von talentierteren Menschen mit C- _Ende zu steigern> C (0) ist es viel effizienter, kleine Finanzbeträge auf viele Einzelpersonen zu verteilen, als auf andere, selektivere Weise zu finanzieren.

Einerseits zeigt das Histogramm, dass das „egalitäre“ Kriterium, das jedem Einzelnen alle 5 Jahre 1 Kapitaleinheit zuweist, die effizienteste Methode zur Verteilung der Finanzen mit E- _Norm = 1 (d. H. E = E _max ) ist: kleine Investitionen F _T in Höhe von 8000 Einheiten, es stellt sich heraus, dass sich der Prozentsatz erfolgreicher talentierter Leute im Vergleich zum Szenario „ohne Finanzierung“ verdoppelt , was von P _T0 = 32,05% auf P _{T führt}= 69,48% mit einem Nettoanstieg von P ^* _T = 37,43. Wenn eine Erhöhung des gesamten investierten Kapitals in Betracht gezogen wird (z. B. durch Festlegung einer Ausgleichsquote von 2 oder 5 Einheiten), stellt diese Strategie auch eine weitere Erhöhung des endgültigen Prozentsatzes erfolgreicher talentierter Mitarbeiter (von 69,48% auf 94,40%) sicher, normalisiert jedoch die Effizienz bei dies nimmt allmählich ab, von E- _Norm = 1 auf E- _Norm = 0,74 bzw. dann auf E- _Norm = 0,37.

Auf der anderen Seite stehen „Elite“ -Strategien, die alle 5 Jahre für eine große Anzahl von Finanzen (5, 10, 15 oder 20 Einheiten) nur unter den besten 50%, 25% oder sogar 10% der bereits erfolgreichen Personen verteilt werden, ganz unten in der Tabelle mitE- _Norm <0,25 In all diesen Szenarien bleibt das Nettowachstum P ^* _{T der} Gesamtzahl erfolgreicher Talente im Vergleich zum Szenario „ohne Finanzierung“ extrem niedrig (in fast allen Fällen weniger als 20%), häufig trotz einer viel größeren Investition Kapital im Vergleich zu einer ähnlichen egalitären Strategie. Diese Ergebnisse bestätigen die Annahme, dass ein solcher Ansatz offensichtlich nicht sehr meritokratisch ist.

Es ist erwähnenswert, dass die Annahme des "gemischten" Kriteriums, d.h. Die Verteilung des „meritokratischen“ Finanzanteils auf einen bestimmten Prozentsatz der erfolgreichsten Personen, beispielsweise 25%, mit der Verteilung der verbleibenden Finanzen zu gleichen Teilen auf andere Personen, führt zu besseren Ergebnissen des Leistungsindex im Vergleich zum „nicht weit meritokratischen“ Ansatz. In Bezug auf die Produktivität kann diese Strategie jedoch das „egalitäre“ Kriterium nicht erfüllen. Wie dies beispielsweise aus einem Vergleich der sechsten und vierten Zeile der Finanzierungstabelle deutlich hervorgeht: Trotz der gleichen Gesamtinvestition von 16.000 Einheiten bleibt der mit den gemischten Kriterien erzielte P _T -Wert viel niedriger als mit dem Nivellierungsansatz (70,83% gegenüber 84, 02%), was auch durch die entsprechenden Werte des Wirkungsgradindex E bestätigt wird_Norm (0,55 vs 0,74).

Wenn wir psychologische Faktoren berücksichtigen (die in dieser Studie nicht modelliert wurden), kann die gemischte Strategie im Vergleich zur egalitären überdacht werden. Tatsächlich kann die Bonusbelohnung, die den erfolgreichsten Personen zugewiesen wird, zu einer stärkeren Einhaltung aller Agenten führen, während der gleichmäßig verteilte Rest eine doppelte Rolle spielt: Auf individueller Ebene wird sie die Vielfalt fördern und erfolglosen talentierten Menschen neue Möglichkeiten bieten, ihr Potenzial auszuschöpfen auf allgemeiner Ebene werden zufällige Entdeckungen unterstützt und damit zur Entwicklung der Forschung und der gesamten Gemeinschaft beigetragen.

Bei erneuter Betrachtung der Tabelle der Finanzierungsstrategien lohnt es sich, auf die unglaublich hohe Effizienz von Zufallsstrategien zu achten, die zwei der drei besten Positionen im Gesamtergebnis einnehmen. Daraus folgt, dass beispielsweise eine periodische Belohnung von 5 Einheiten von nur 10% zufällig ausgewählter Personen mit einer Gesamtinvestition von nur 4.000 Einheiten eine Nettoerhöhung von P ^* _T = 17,78% ergibt, was höher ist als bei fast allen, die durch Ausgleich erzielt werden Strategien. Darüber hinaus führt eine Erhöhung des Anteils zufällig finanzierter Personen auf 25% und eine Verdoppelung der Gesamtinvestition (Erhöhung auf 10.000 Einheiten) zu einem Nettowachstum von P ^* _T.= 35,95, vergleichbar mit der besten Ausgleichsstrategie, die den ersten Platz in der Gesamtwertung gewann. Es fällt auf, dass dieses letzte P ^* _T- Ergebnis etwa das Vierfache des Wertes ( P ^* _T) beträgt = 9,03%) erhalten unter Verwendung des elitären Ansatzes (siehe Zeile 12 der Tabelle), der genau das gleiche Kapital (10.000 Einheiten) auf die gleiche Anzahl von Individuen (25% der Gesamtzahl) verteilte. Letzteres bestätigt noch mehr, dass in komplexen sozialen und wirtschaftlichen Umgebungen, in denen der Zufall eine bedeutende Rolle spielt, die Wirksamkeit anderer Strategien, die auf zufälligen Wahlen basieren, Standardstrategien, die auf dem „fast meritokratischen“ Ansatz basieren, leicht umgehen kann. Dieses Phänomen wurde entgegen dem gesunden Menschenverstand bereits in den Bereichen Management, Politik und Finanzen beobachtet [48, 49, 50, 51, 52, 53, 54, 55] und findet somit im Rahmen der Finanzierungsstudie eine weitere Bestätigung.

Um die erhaltenen Daten weiter zu bestätigen, zeigt Fig. 12 die Ergebnisse einer anderen Reihe von Simulationen. Im Gegensatz zu früheren Simulationen ist hier der Gesamtbetrag des in jeden der 100 Läufe investierten Kapitals jetzt auf F _T = 80.000 festgelegt, so dass F _T / 8 = 10.000 Einheiten gemäß den zuvor diskutierten Finanzierungsstrategien alle 5 Jahre auf die Agenten verteilt werden . Wenn wir uns die Tabelle ansehen, sehen wir, dass die Ergebnisse der Ausgleichsstrategie erneut am effektivsten waren, um die talentiertesten Leute mit einem Anteil von P _{T zu} belohnennahe 100%. Darauf folgt eine zufällige Strategie (wobei 50% der Personen zufällig für die Finanzierung ausgewählt werden), die dann gemischt wird, wobei die Hälfte des Kapitals unter 25% der erfolgreichsten Personen und der andere Teil zu gleichen Teilen unter anderen Personen verteilt wird. Im Gegenteil, alle Elitestrategien befanden sich erneut am Ende des Ratings, was die Ineffizienz des „nicht weit meritokratischen“ Ansatzes bei der Belohnung wahrer Talente weiter bestätigte.


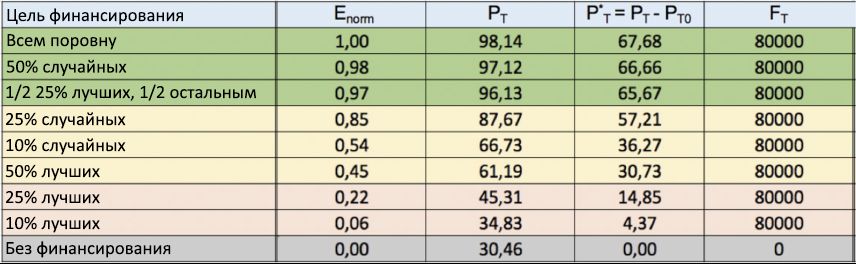Abbildung 12: Tabelle der Finanzierungsstrategien für feste Finanzierungen. Die erhaltenen normalisierten Effizienzindizes E- _Norm für mehrere Strategien zur Finanzierungsverteilung (1. Spalte) werden wieder in absteigender Reihenfolge von oben nach unten angezeigt. Im Gegensatz zu Abbildung 10 ist hier das in jeden Lauf investierte Gesamtkapital auf festgelegtF _T = 80.000. Die Ausgleichsstrategie belegte erneut den ersten Platz.

Die in diesem Unterabschnitt vorgestellten Ergebnisse von Simulationen des TPU-Modells machten auf die Bedeutung externer Faktoren (als tatsächlich wirksame Finanzierungspolitik) für die Erhöhung der Erfolgschancen für die meisten talentierten Personen aufmerksam, die zu oft durch das Zusammentreffen erfolgloser Ereignisse bestraft werden. Im nächsten Unterabschnitt untersuchen wir, inwieweit sich aus Umweltveränderungen neue Möglichkeiten ergeben sollten, z. B. das Bildungsniveau oder andere Anreize, die sich aus dem sozialen Umfeld ergeben, in dem Menschen leben oder aus dem sie stammen.

3.2. Bedeutung der Umwelt

Lassen Sie uns zunächst die Rolle des durchschnittlichen Bildungsniveaus in der Bevölkerung bewerten. Im Rahmen des TPU-Modells kann es durch Ändern der Parameter der Normalverteilung von Talenten erhalten werden. Wenn wir im Allgemeinen davon ausgehen, dass das Talent und die Fähigkeiten von Individuen, wenn sie stimuliert werden, bei der Realisierung neuer Möglichkeiten effektiver sein können, kann der Anstieg entweder des Medians m _T oder der Standardabweichung von Talent σ _T als Folge der jeweils angestrebten Politik interpretiert werden Erhöhung des durchschnittlichen Bildungsniveaus oder Stärkung der Ausbildung der begabtesten Menschen.

In den beiden Diagrammen von Abbildung 13 haben wir das Gesamtkapital / den Gesamterfolg der besten Leistungsträger jedes der 100 Läufe in Form einer Funktion ihres Talents dargestellt. Die angegebenen Parameter entsprechen denen in Unterabschnitt 2.2 ( N = 1000, I = 80, δ _t = 6, C (0) = 10, N _E = 500 und p _L = 50%), jedoch mit unterschiedlichen Momenten der Talentverteilung . Insbesondere wird in dem Diagramm (a) unverändert gelassen wir m _T = 0,6, aber erhöht σ _T = 0,2, während sie in dem Diagramm (b) aus entgegengesetzt, so dass σ _T = 0,1 und Hebe m_T = 0,7. In beiden Fällen können Sie eine Verschiebung nach rechts von den Spitzen des maximalen Erfolgs feststellen, jedoch mit unterschiedlichen Details.


Abbildung 13: Das Gesamtkapital der erfolgreichsten Personen in jedem der 100 Läufe, dargestellt als Funktion ihres Talents für Bevölkerungsgruppen mit unterschiedlichen Parametern der Talentverteilung: (a) m _T = 0,6 und σ _T = 0,2 (was die Stärkung des Akademikers widerspiegelt Ausbildung der begabtesten Menschen); (b) m _T = 0,7 und σ _T = 0,1 (was einen Anstieg des durchschnittlichen Bildungsniveaus darstellt). Die entsprechenden Werte von m _T und m _T ± σ _T sind ebenfalls gezeigt.in Form von vertikalen gestrichelten Linien bzw. gepunkteten Linien.

Tatsächlich führt dies dazu, dass eine Erhöhung von σ _T bei einem konstanten Wert von m _T , wie in Abbildung (a) gezeigt, die Chancen der talentiertesten Leute erhöht , einen sehr hohen Erfolg zu erzielen - der beste Darsteller ist jetzt ein sehr begabter Agent mit T = 0, 97 haben das unglaubliche Niveau Kapital / Erfolg erreicht C _best = 655360. es ist auf der einen Seite kann es jedoch zu erkennen, wird auf der anderen Seite, ein Einzelfall ist und wird auch als ein Gegengewicht, die Wachstumslücke zwischen Glück und glücklichen Menschen beobachtet. Wenn wir uns nun Schema (b) ansehen, sehen wir, dass der Anstieg von m _T.ohne Änderung von σ _T ergibt sich der beste Performer mit C _best = 327680 und Talent T = 0,8, gefolgt von zwei weiteren mit C = 163840 und dementsprechend T = 0,85 und T = 0,92. Dies deutet darauf hin, dass in diesem Fall die Chancen der talentiertesten Menschen auf einen extrem hohen Erfolg gestiegen sind, gleichzeitig aber die Kluft zwischen unglücklichen und glücklichen Menschen geringer war als zuvor.

Schließlich stieg in beiden betrachteten Beispielen der durchschnittliche Wert des Kapitals / Erfolgs des talentiertesten von 100 Personengruppen im Verhältnis zu dem in Unterabschnitt 2.2 erhaltenen Wert von C _mt ≈ 63. Insbesondere haben wir C._mt ≈ 319 in Schema (a) und C _mt ≈ 122 in Schema (b), aber diese Ergebnisse sind für eine bestimmte Reihe von Simulationsläufen sehr spezifisch. Ein zuverlässigerer Parameter für den numerischen Ausdruck der Wirksamkeit der hier untersuchten Sozialpolitik ist, dass es sich wieder um denim vorherigen Unterabschnitt dargestelltenIndikator P _{T handelt} , d. H. durchschnittlicher Anteil von Personen mit Talent T > m _T + σ _T und Gesamterfolg / Kapital C _end > 10, bezogen auf die Gesamtzahl der Personen mit Talent T > m _T + σ _T (beachten Sie, dass hier in beiden Fällenm _T + σ _T = 0,8). Wir haben also P _T = 38% in Schema (a) und P _T = 37,5% in Schema (b) mit einem leichten Nettoanstieg gegenüber dem Referenzwert P _T0 = 32% (erhalten für die Talentverteilung bei m _T) = 0,6 und σ _T = 0,1).

Zusammenfassend zeigen unsere Ergebnisse, dass die Stärkung der Ausbildung der begabtesten Menschen oder die Erhöhung des durchschnittlichen Bildungsniveaus erwartungsgemäß zu einigen positiven Auswirkungen auf das Sozialsystem führt, da beide Maßnahmen zu einer Erhöhung der Wahrscheinlichkeit führen, dass talentierte Personen Chancen nutzen. gewährte ihnen Glück. Andererseits scheint die Verbesserung des durchschnittlichen Anteils hochtalentierter Personen, die ein gutes Erfolgsniveau erreicht haben, für beide analysierten Szenarien nicht besonders bedeutend zu sein. Daher scheint das Ergebnis der einschlägigen Bildungspolitik weitgehend auf das Auftreten von Einzelfällen mit außergewöhnlichem Erfolg beschränkt zu sein.

Sobald dieses Bildungsniveau erreicht war, wurde natürlich klar, dass die Fülle an Möglichkeiten, die dieses soziale Umfeld bietet, d.h. Das Land, in dem jemand versehentlich geboren wurde oder sich für ein Leben entschieden hat, ist eine weitere Schlüsselkomponente, die die globale Leistung des Systems beeinflussen kann.

In Abbildung 14 haben wir ähnliche Ergebnisse wie im vorherigen Bild dargestellt, jedoch für eine andere Reihe von Simulationen mit jeweils 100 Läufen mit denselben eingestellten Parametern wie in Unterabschnitt 2.2 ( N = 1000, m _T = 0, 6, & sgr; _T = 0,1, I = 80, C (0) = 10, N _E = 500), jedoch mit unterschiedlichen Prozentsätzen p _L.erfolgreiche Ereignisse (erinnern Sie sich, dass in Unterabschnitt 2.2 der Prozentsatz p _L = 50% genommen wurde ). In Schema (a) nehmen wir p _L = 80%, um ein hoch stimulierendes Umfeld voller Möglichkeiten zu simulieren, das typisch für reiche Industrieländer wie die USA ist [26]. Andererseits gibt in Schema (b) ein Wert von p _L = 20% ein Szenario eines viel weniger ermutigenden Umfelds mit einer äußerst geringen Anzahl von Möglichkeiten wieder, wie beispielsweise in Ländern der Dritten Welt.


Abbildung 14: Das Gesamtkapital der erfolgreichsten Personen in jedem der 100 Läufe wird als Funktion ihres Talents für Bevölkerungsgruppen gezeigt, die in Umgebungen mit unterschiedlichen Prozentsätzen p _L erfolgreicher Ereignisse leben: (a) p_L = 80%; (b) p _L = 20%. Vertikale gestrichelte und gepunktete Linien markieren auch die Werte von m _T = 0,6 und m _T ± σ _T mit σ _T = 0,1.

Wie in beiden Systemensehen, sind die endgültige Erfolg / Kapital glücklichsten Menschen in Abhängigkeit von ihrem Talent gezeigt, stark abhängig von p _L .

Bei p _L = 80% konnten wie in Schema (a) mehrere Agenten mit mittlerem bis hohem Talent höhereErfolgsniveauserzielen als im Szenario p _L = 50% mit Peak C._best = 163840. Andererseits ist der durchschnittliche Kapitalwert / Erfolg der talentiertesten Personen, C _mt ≈ 149, ziemlich hoch, und was noch wichtiger ist, dies gilt auch für den Indikator P _T = 62,18% (was ungefähr doppelt so viel ist Referenzwert P _T0 = 32%) bedeutet dies, dass die talentiertesten Menschen erwartungsgemäß von einem größeren Prozentsatz erfolgreicher Veranstaltungen profitieren.

Völlig unterschiedliche Ergebnisse wurden mit p _L = 20% erhalten. Natürlich ist, wie aus Schema (b) ersichtlich, das Gesamterfolgsniveau jetzt sehr niedrig im Vergleich zu dem, was in den Simulationen aus Unterabschnitt 2.2 gefunden wurde, mit einem Spitzenwert von C am _bestenDies entspricht einer Verringerung der sozialen Ungleichheiten, was die erwartete Folge der Chancengleichheit für den Erfolg ist. In Übereinstimmung mit diesen Ergebnissen erreicht der Indikator P _T auch einen Mindestwert, wobei ein durchschnittlicher Prozentsatz talentierter Personen, denen es gelungen ist, ihren anfänglichen Erfolg zu steigern, nur 8,75% beträgt.

In diesem Abschnitt wurde daher gezeigt, dass das ermutigende Umfeld und die Fülle an Möglichkeiten, die mit der geeigneten Strategie für die Zuweisung von Finanzen und Ressourcen verbunden sind, wichtige Faktoren für die Realisierung des Potenzials der talentiertesten Menschen sind und ihnen mehr Erfolgschancen bieten als mäßig begabte, aber mehr Glück. Aus makroökonomischer Sicht wird jede Politik, die diese Indikatoren beeinflussen und talentierte Einzelpersonen unterstützen kann, zu kollektivem Fortschritt und Innovation führen.

4. Schlussbemerkungen

In diesem Artikel haben wir ausgehend von einer Reihe äußerst einfacher und rationaler Annahmen ein Agentenmodell vorgestellt, mit dem die Rolle von Talent und Glück für den Erfolg der Karriere von Menschen quantitativ gemessen werden konnte. Die Simulationen zeigten, dass, obwohl das Talent eine Gaußsche Verteilung unter den Agenten aufweist, die endgültige Verteilung von Erfolg / Kapital nach 40 Jahren Arbeitsleben einer Machtfunktion nach dem Prinzip des Pareto-Gesetzes „80/20“ folgt, die der Art der in der realen Welt beobachteten Verteilung des Reichtums entspricht. Ein wichtiges Ergebnis der Simulationen ist, dass die erfolgreichsten Agenten fast immer nicht die talentiertesten sind, sondern diejenigen, die nahe am Durchschnittswert der Gaußschen Talentverteilung liegen - eine weithin bekannte Tatsache, die häufig in der Literatur zu finden ist.Das Modell zeigt die oft unterschätzte Bedeutung erfolgreicher Veranstaltungen für die Bestimmung des endgültigen Niveaus des individuellen Erfolgs. Da Belohnungen und Ressourcen in der Regel an diejenigen verteilt werden, die bereits ein hohes Maß an Erfolg erzielt haben und fälschlicherweise als Maß für Kompetenz / Talent verwendet werden, führt dies zu einem negativen Anreiz, der zu einem Mangel an Möglichkeiten für die höchsten Talente führt. Unsere Ergebnisse unterstreichen die Risiken eines Paradigmas, das wir als „Near Meritocracy“ bezeichnen und das die kompetentesten Menschen nicht respektieren und belohnen kann, da es die Rolle des Zufalls unter den wichtigsten Erfolgsfaktoren unterschätzt. In diesem Zusammenhang wurden verschiedene Szenarien untersucht, um die effektivsten Strategien zu ermitteln, mit denen die unvorhersehbare Rolle des Glücks ausgeglichen und den talentiertesten mehr Möglichkeiten und Ressourcen geboten werden können - die Absicht,Das sollte das Hauptziel eines wirklich meritokratischen Ansatzes sein. Es wurde auch gezeigt, dass diese Strategien für die gesamte Gemeinschaft am vorteilhaftesten sind, da sie zum Wachstum verschiedener Ideen und Perspektiven in der Forschung führen und damit auch die Innovation anregen.

Danksagung

Wir möchten Robert Frank, Pavel Sobkowitz und Konstantino Tsallis für fruchtbare Diskussionen und Kommentare danken.

Bibliographie

1. Bak, P., Tang, C. und Wiesenfeld, K., Selbstorganisierte Kritikalität. Phys. Rev. A , 38: 364 {374 (1988).
2. Barab´asi, A.-L., Albert, R., Emergence of Scaling in Random Networks, Science , Vol. 3, No. 286, Ausgabe 5439, pp. 509 {512 (1999).
3. Newman, MEJ, Potenzgesetze, Pareto-Verteilungen und Zipf-Gesetz, Contemporary Physics , 46 (5): 323 {351 (2005).
4. Tsallis, C., Einführung in die nicht umfangreiche statistische Mechanik. Annäherung an eine komplexe Welt , Springer (2009).
5. Pareto, V., Cours d'Economique Politique , vol. 2 (1897).
6. Steindl, J., Random Processes and the Growth of Firms — A Study of the Pareto Law, Charles Griffin and Company , London (1965).
7. Atkinson, AB, Harrison, AJ, Distribution of Total Wealth in Britain, Cambridge University Press , Cambridge (1978).
8. Persky, J., Retrospectives: Pareto's law, Journal of Economic Perspectives 6, 181{192 (1992).
9. Klass, OS, Biham, O., Levy, M., Malcai, O., Solomon, S., The Forbes 400 and the Pareto wealth distribution, Economics Letters 90, 290{295 (2006).
10. Hardoon, D., An economy for the 99% , Oxfam GB, Oxfam House, John Smith Drive, Cowley, Oxford, OX4 2JY, UK (January 2017).
11. Bouchaud, J.-P., M´ezard, M., Wealth condensation in a simple model of economy, Physica A 282, 536{54 (2000).
12. Dragulescu, A. and Yakovenko, VM, Statistical mechanics of money, Eur. Phys. J. B 17, 723{729 (2000).
13. Chakraborti, A. and Chakrabarti, BK, Statistical mechanics of money: how saving propensity affects its distribution, Eur. Phys. J. B 17, 167{170 (2000).
14. Patriarca, M., Chakraborti, A., Germano, G., Influence of saving propensity on the power law tail of wealth distribution, Physica A 369(2), 723{736 (2006).
15. Scalas, E., Random exchange models and the distribution of wealth. European Physical Journal — Special Topics , 225. pp. 3293-3298. ISSN 1951{6355 (2016).
16. During, B., Georgiou, N. and Scalas, E., A stylised model for wealth distribution. In Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95{117. ISBN 9789811057045 (2017).
17. During, Bertram, Georgiou, Nicos and Scalas, Enrico (2017) A stylised model for wealth distribution. In: Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95-117. ISBN 9789811057045
18. Sinatra, R., Wang, D., Deville, P., Song, C. and Barab´asi, A.-L., Quantifying the evolution of individual scientific impact, Science 354, 6312 (2016).
19. Einav, L. and Yariv, L., What's in a Surname? The Effects of Surname Initials on Academic Success, Journal of Economic Perspective , Vol. 20, n. 1, p.175{188 (2006).
20. Ruocco, G., Daraio, C., Folli, V. and Leonetti, M., Bibliometric indicators: the origin of their log-normal distribution and why they are not a reliable proxy for an individual scholar's talent, Palgrave Communications 3:17064 doi: 10.1057/palcomms.2017.64 (2017).
21. Jurajda, S., Munich, D., Admission to Selective Schools, Alphabetically, Economics of Education Review , Vol. 29, n. 6, p.1100{1109 (2010).
22. Van Tilburg, WAP, Igou, ER, The impact of middle names: Middle name initials enhance evaluations of intellectual performance, European Journal of Social Psychology , Vol. 44, Issue 4, p.400{411 (2014).
23. Laham, SM, Koval, P., Alter, AL, The name-pronunciation effect: Why people like Mr. Smith more than Mr. Colquhoun, Journal of Experimental Social Psychology 48, p.752{756 (2012).
24. Silberzahn, R., Uhlmann, EL, It Pays to be Herr Kaiser: Germans with Noble-Sounding Last Names More Often Work as Managers, Psychological Science 24(12): 2437{44 (2013).
25. Coffey, B. and McLaughlin, P., From Lawyer to Judge: Advancement, Sex, and NameCalling. SSRN Electronic Journal , DOI10.2139/ssrn.1348280 (2009).
26. Milanovic, B., Global Inequality of Opportunity: How Much of Our Income Is Determined by Where We Live?, Review of Economics and Statistics , 97.2 (2015): 452{60.
27. Du, Q., Gao, H., Levi, MD, The relative-age effect and career success: Evidence from corporate CEOs, Economics Letters 117(3):660{662 (2012).
28. Deaner, RO, Lowen, A., Cobley, S., Born at the Wrong Time: Selection Bias in the NHL Draft. PLoS ONE 8(2): e57753 (2013).
29. Brooks, D., The Social Animal. The Hidden Sources of Love, Character, and Achievement, Random House , 424 pp. (2011).
30. Iacopini, I., Milojevic, S. and Latora, V., Network Dynamics of Innovation Processes, Physical Review Letters 120, 048301 (2018).
31. Tomasetti, C., Li, L., Vogelstein, B., Stem cell divisions, somatic mutations, cancer etiology, and cancer prevention, Science 355, 1330{1334 (2017).
32. Newgreen, DF et al., Differential Clonal Expansion in an Invading Cell Population: Clonal Advantage or Dumb Luck?, Cells Tissues Organs 203:105{113 (2017).
33. Snyder, RE and Ellner, SP, We Happy Few: Using Structured Population Models to Identify the Decisive Events in the Lives of Exceptional Individuals, The American Naturalist 188, no. 2 (2016): E28{E45.
34. Snyder, RE and Ellner, SP, Pluck or Luck: Does Trait Variation or Chance Drive Variation in Lifetime Reproductive Success?, The American Naturalist 191, no. 4 (2018): E90{E107.
35. .., . , , (2018).
36. .., . , (2018).
37. Mauboussin, MJ, The Success Equation: Untangling Skill and Luck in Business, Sports, and Investing, Harvard Business Review Press (2012).
38. .., . , (2019).
39. Watts, DJ, Everything Is Obvious: Once You Know the Answer , Crown Business (2011).
40. Salganik, MJ, Dodds PS, Watts DJ, Experimental Study of Inequality and Unpredictability in an Artificial Cultural Market, Science Vol.311 (2006)
41. Travis, M., Hofman, JM, Sharma, A., Anderson,. A., Watts, DJ, Exploring limits to prediction in complex social systems , Proceedings of the 25th ACM International World Wide Web Conference (2016) arXiv:1602.01013 [cs.SI]
42. Stewart, J., The Distribution of Talent, Marilyn Zurmuehlin Working Papers in Art Education 2 : 21-22 (1983).
43. Sinha, S. and Pan, RK, How a «Hit» is Born: The Emergence of Popularity from the Dynamics of Collective Choice, In Econophysics and Sociophysics: Trends and Perspectives (eds BK Chakrabarti, A. Chakraborti and A. Chatterjee), Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany. doi: 10.1002/9783527610006.ch15 (2006).
44. Fortin, J.-M., Curr, DJ, Big Science vs. Little Science: How Scientific Impact Scales with Funding, PLoS ONE 8(6): e65263 (2013).
45. Jacob, BA, Lefgren, L., The impact of research grant funding on scientific productivity, Journal of Public Economics 95 (2011) 1168{1177.
46. O'Boyle, JR. E. and Aguinis, H., The Best and the Rest: revisiting the norm of normality of individual performance, Personnel Psychology , 65: 79-119. doi:10.1111/j.1744-6570.2011.01239.x (2012).
47. Denrell, J. and Liu, C., Top performers are not the most impressive when extreme performance indicates unreliability, Proceedings of the National Academy of Sciences , 109(24):9331{9336 (2012).
48. Pluchino, A., Rapisarda, A., and Garofalo, C., The Peter principle revisited: A computational study, Physica A 389(3):467{472 (2010).
49. Pluchino, A., Garofalo, C., Rapisarda, A., Spagano, S. and Caserta, M., Accidental politicians: How randomly selected legislators can improve parliament efficiency, Physica A 390(21):3944{3954 (2011).
50. Pluchino, A., Rapisarda, A. and Garofalo, C., Efficient promotion strategies in hierarchical organizations, Physica A 390(20):3496{3511 (2011).
51. Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Reducing financial avalanches by random investments, Phys. Rev. E 88(6):062814 (2013).
52. Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Are random trading strategies more successful than technical ones, PLoS One 8(7):e68344 (2013)
53. Biondo, AE, Pluchino, A., Rapisarda, A., The beneficial role of random strategies in social and financial systems, J. Stat. Phys. 151(3-4):607{622 (2013).
54. Biondo, AE, Pluchino, A., Rapisarda, A., Micro and macro benefits of random investments in financial markets, Cont. Phys. 55(4):318{334 (2014).
55. Biondo, AE, Pluchino, A., Rapisarda, A., Modeling financial markets by self-organized criticality, Phys. Rev. E 92(4):042814 (2015).
56. Wilensky, U., NetLogo. ccl.northwestern.edu/netlogo . Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL (1999).
57. Merton, RK, The Matthew effect in science, Science 159, 56-63 (1968).
58. . ., , II: , https://www.hse.ru/data/033/314/1234/3_6_1Merto.pdf .
59. Bol, T., de Vaan, M. and van de Rijt, A., The Matthew effect in science funding, Proceedings of the National Academy of Sciences , DOI: 10.1073/pnas.1719557115 (2018).
60. Mongeon, P., Brodeur, C., Beaudry, C. et al., Concentration of research funding leads to decreasing marginal returns, Research Evaluation 25, 396{404 (2016).
61. Merton, RK, Barber, E., The Travels and Adventures of Serendipity , Princeton University Press, Princeton (2004).
62. Murayama, K. et al., Management of science, serendipity, and research performance, Research Policy 44 (4), 862{873 (2015).
63. Benias, PC et al., Structure and Distribution of an Unrecognized Interstitium in Human Tissues, Scientific Reports , vol. 8, 4947 (2018).
64. Flexner, A, The Usefulness of Useless Knowledge , Princeton University Press, Princeton (2017).
65. Lucky science. Scientists often herald the role of serendipity in research. A project in Britain aims to test the popular idea with evidence. , Nature Editorial, Vol.554, 1 February 2018.
66. Yaqub, O., Serendipity: Towards a taxonomy and a theory, Research Policy 47, 169{179 (2018).
67. Page, SE, The Diversity Bonus. How Great Teams Pay Off in the Knowledge Economy , Princeton University Press (2017).
68. Cimini, G., Gabrielli, A., Sylos Labini, F., The Scientific Competitiveness of Nations, PLoS ONE 9(12): e113470. doi.org/10.1371/journal.pone.0113470 (2014).
69. Curry, S., Let's move beyond the rhetoric: it's time to change how we judge research, Nature 554, 147 (2018).
70. Nicholson, JM and Ioannidis, JPA, Research grants: Conform and be funded, Nature 492, 34{36 (2012).
71. Bollen, J., Crandall, D., Junk, D. et al., An efficient system to fund science: from proposal review to peer-to-peer distributions, Scientometrics 110, 521{528 (2017).
72. Garner, HR, McIver, LJ and Waitzkin, MB, Research funding: Same work, twice the money?, Nature 493,599{601 (2013).

: Talent vs Luck: the role of randomness in success and failure