Ausgewogene binäre Suchbäume: Implementierung auf Julia

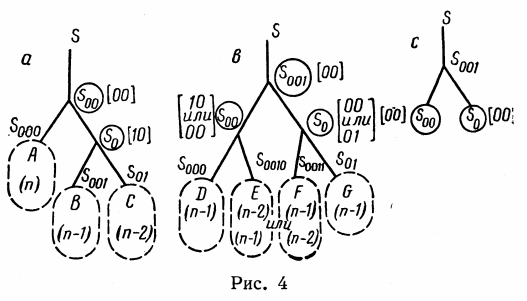
Illustration aus der Arbeit von G.M. Adelson-Welsky und E.M. Landis 1962

Suchbäume sind Datenstrukturen für die ordnungsgemäße Speicherung und einfache Suche nach Elementen. Binäre Suchbäume sind weit verbreitet, bei denen jeder Knoten nur zwei untergeordnete Knoten hat. In diesem Artikel betrachten wir zwei Methoden zum Organisieren von binären Suchbäumen: die Adelson-Welsky- und Landis-Algorithmen (AVL-Bäume) und geschwächte AVL-Bäume (WAVL-Bäume).

Beginnen wir mit den Definitionen. Der Binärbaum besteht aus Knoten , jeder Knoten speichert einen Datensatz in Form von Schlüssel-Wert- Paaren (oder im einfachen Fall nur Werten) und hat nicht mehr als zwei untergeordnete Knoten. Nachkommenknoten werden durch rechts und links unterschieden , und die Bedingung für die Reihenfolge der Schlüssel ist erfüllt: Der Schlüssel des linken Nachkommen ist nicht mehr und der rechte ist nicht kleiner als der Schlüssel des übergeordneten Knotens. Darüber hinaus können Dienstinformationen in Knoten gespeichert werden (und normalerweise in Knoten gespeichert werden) - beispielsweise eine Verknüpfung zum übergeordneten Knoten oder andere Daten. Sonderfälle sind der Stammknoten, von dem aus der Baum eingegeben wird, und ein leerer Knoten , der keine Informationen speichert. Knoten, in denen beide Nachkommen leer sind, werden Baumblätter genannt. Ein Knoten mit allen Nachkommen bildet einen Teilbaum . Somit ist jeder Knoten entweder die Wurzel eines Teilbaums oder eines Blattes.

Mit dieser Definition können Sie eine einfache Struktur zum Speichern von Knoten und des Baums selbst erstellen. Wir nehmen an, dass ein leerer Knoten den speziellen Wert nothing Typ Nothing . Dann reicht es aus, im Knoten Verweise auf den rechten und linken Nachwuchs sowie auf den Elternteil zu speichern. Die Struktur zum Speichern des Baums enthält nur eine Verknüpfung zum Stammknoten.

 # K -   # V -    mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} end mutable struct BST{K, V} root::BSTNode{K,V} end 

In diesem Fall stellt sich die Frage, wie ein leerer Baum dargestellt werden soll. Dazu verwenden wir den Ansatz aus dem Buch "Algorithmen: Konstruktion und Analyse" und fügen als Eintrittspunkt in den Baum keine Wurzel, sondern einen Dummy-Knoten ein, der sein eigenes übergeordnetes Element sein wird. Fügen Sie der BSTNode-Strukturbeschreibung Konstruktoren hinzu, um einen solchen Knoten zu erstellen:

 mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} #   function BSTNode{K,V}() where {K,V} node = new{K,V}() node.parent = node node.left = node.right = nothing return node end #    - function BSTNode{K,V}(key, value) where {K, V} node = new{K,V}() node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end BSTNode() = BSTNode{Any, Any}() #     ! struct BST{K, V} entry::BSTNode{K,V} BST{K,V}() where {K,V} = new{K,V}(BSTNode{K,V}()) end BST() = BST{Any, Any}() Base.isempty(bst::BST) = bst.entry.left == nothing 

In diesem Fall kann die BST Struktur unverändert gemacht werden, weil Der Link zum Einstiegspunkt muss nicht mehr geändert werden. Ferner nehmen wir an, dass der Wurzelknoten des Baums unmittelbar der rechte und linke Nachkomme des Eingabeknotens ist.

Die Hauptoperation, für die Suchbäume benötigt werden, ist natürlich die Suche nach Elementen. Da der Schlüssel des linken untergeordneten Elements nicht mehr und der rechte nicht kleiner als der übergeordnete Schlüssel ist, wird die Elementsuchprozedur sehr einfach geschrieben: Vergleichen Sie ausgehend von der Wurzel des Baums den Eingabeschlüssel mit dem Schlüssel des aktuellen Knotens; Wenn die Schlüssel übereinstimmen, geben wir den Wert zurück. Andernfalls gehen Sie je nach Reihenfolge der Schlüssel zum linken oder rechten Teilbaum. Wenn sie gleichzeitig einen leeren Knoten erreicht haben - es gibt keinen Schlüssel im Baum, lösen Sie eine Ausnahme aus.

 #   Base.getindex()    #      tree[key] function Base.getindex(bst::BST{K,V}, key) where {K,V} key = convert(K, key) node = bst.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end 

Das Suchen nach einem Element mit einem Schlüssel dauert offensichtlich O ( h ) Zeit, wobei h die Höhe des Baums ist, d.h. maximaler Abstand von Wurzel zu Blatt. Es ist leicht zu berechnen, dass ein Binärbaum der Höhe h höchstens 2 ^{h + 1} -1 Knoten enthalten kann, wenn er dicht besiedelt ist , d. H. Alle Knoten außer vielleicht der extremsten Schicht haben beide Nachkommen. Darüber hinaus ist klar, dass jede gegebene Tastenfolge im Voraus zu einem so dichten Baum führen kann. Dies ergibt ein sehr optimistisches asymptotisches Verhalten bei der Suche nach einem Element in einem Baum mit seiner optimalen Konstruktion in der Zeit O (log ₂ N ), wobei N die Anzahl der Elemente ist.

Natürlich muss der Algorithmus zum Hinzufügen eines Elements zum Suchbaum so konstruiert sein, dass die Bedingung für die Reihenfolge der Schlüssel erfüllt ist. Schreiben wir eine naive Implementierung des Einfügens eines Elements per Schlüssel:

 #   Base.setindex!()    #       tree[key] = value function Base.setindex!(bst::BST{K,V}, val::SV, key::SK) where {K, V} key, value = convert(K, key), convert(V, val) parent = bst.entry.left #   -     if parent == nothing newnode.parent = bst.entry bst.entry.left = bst.entry.right = newnode return val end key_found = false while !key_found if key < parent.key if parent.left == nothing parent.left = BSTNode{K,V}(key, value) parent.left.parent = parent key_found = true else parent = parent.left end elseif key > parent.key if parent.right == nothing parent.right = BSTNode{K,V}(key, value) newnode.parent = parent key_found = true else parent = parent.right end else key_found = true parent.value = value end end return val end 

Leider ergibt die naive Konstruktion des Baums die gewünschte Struktur nur bei zufälligen Eingabedaten, aber in Wirklichkeit sind sie oft recht strukturiert. Im schlimmsten Fall, wenn die eingehenden Schlüssel streng geordnet sind (zumindest in aufsteigender, mindestens in absteigender Reihenfolge), sendet die naive Baumkonstruktion ständig neue Elemente in eine Richtung und sammelt tatsächlich eine lineare Liste. Es ist leicht zu erraten, dass das Einfügen von Elementen, dass die Suche mit einer solchen Struktur während O ( N ) stattfinden wird, was alle Bemühungen zum Aufbau einer komplexen Datenstruktur zunichte macht.

Schlussfolgerung: Der Suchbaum muss während der Erstellung ausgeglichen werden, d. H. Richten Sie die Höhe des rechten und linken Teilbaums an jedem Knoten aus. Es gibt verschiedene Ansätze zum Auswuchten. Am einfachsten ist es, eine bestimmte Anzahl von Einfüge- oder Löschvorgängen anzugeben, nach denen der Baum neu ausgeglichen wird. In diesem Fall befindet sich der Baum vor dem Auswuchten in einem eher "laufenden" Zustand, weshalb das Auswuchten im schlimmsten Fall etwa 0 ( N ) Zeit in Anspruch nimmt, aber nachfolgende Operationen bis zu einem bestimmten Einfüge- / Löschschwellenwert in logarithmischer Zeit ausgeführt werden. Eine andere Möglichkeit besteht darin, die Einfüge- und Löschalgorithmen sofort so zu erstellen, dass der Baum immer ausgeglichen bleibt, was die garantierte Zeitkomplexität O (log ₂ N ) für jede Operation ergibt.

Aufgrund der Tatsache, dass es Algorithmen gibt, bei denen der Baum „wild werden“ darf, aber danach Operationen für eine ziemlich lange Zeit in einer logarithmischen Zeit ausgeführt werden können, bevor der Baum für eine lange Zeit wieder in einen ausgeglichenen Zustand gebracht werden muss, wird die garantierte und amortisierte Zeit des Einfügens / Löschens eines Elements unterschieden. Bei einigen Implementierungen von Operationen mit binären Suchbäumen ist die Komplexität des Einfügens und Löschens von O (log ₂ N ) garantiert, bei einigen wird es mit einer Verschlechterung auf O ( N ) abgeschrieben.

Adelson-Welsky- und Landis-Algorithmus (AVL)

Die erste Implementierung eines selbstausgleichenden binären Suchbaums wurde 1962 von Adelson-Welsky und Landis vorgeschlagen. In der modernen Literatur zu den Anfangsbuchstaben von Nachnamen wird diese Struktur als AVL-Bäume bezeichnet . Die Struktur wird durch die folgenden Eigenschaften beschrieben:

1. Reihenfolge: Für jeden Knoten ist der Schlüssel oben im linken Teilbaum kleiner als der Schlüssel oben im rechten Teilbaum (wenn die Nachkommen keine leeren Knoten sind).
2. Höhenerhöhung: Die Höhe des übergeordneten Knotens ist um eins höher als die maximale Höhe seiner Nachkommen. Die Höhe der leeren Knoten kann als gleich Null betrachtet werden.
3. AVL-Balance: Für jeden Knoten unterscheiden sich die Höhen der rechten und linken Teilbäume um nicht mehr als 1.

Aus diesen Eigenschaften folgt, dass die Höhe des gesamten Baums O ist (log ₂ N ), wobei N die Anzahl der im Baum gespeicherten Datensätze ist, was bedeutet, dass der Datensatz in logarithmischer Zeit gesucht wird. Damit der Zustand des ABL-Gleichgewichts nach jedem Einsetzen erhalten bleibt, wird jedes Einsetzen von einem Ausgleichsvorgang begleitet. Für die effektive Implementierung dieser Operation muss jeder Knoten Dienstinformationen speichern. Halten Sie der Einfachheit halber einfach die Höhe des Knotens dort.

 mutable struct AVLNode{K,V} # ,       255 # (  10^38 ) height::UInt8 key::K value::V left::Union{Nothing, AVLNode{K,V}} right::Union{Nothing, AVLNode{K,V}} parent::AVLNode{K,V} #   function AVLNode{K,V}() where {K,V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing return node end #    - function AVLNode{K,V}(key::SK, value::SV) where {K, V, SK<:K, SV<:V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end avlheight(node::Union{Nothing,AVLNode}) = node == nothing ? 0 : Int(node.height) 

Datensatz einfügen

Das grundlegende Einfügen erfolgt gemäß dem Standardalgorithmus. Gehen Sie den Baum nach unten, suchen Sie, wo Sie einen neuen Knoten einfügen und einfügen können. Wir werden Wrapper schreiben, um untergeordnete Knoten mithilfe der Indizes -1 und 1 anstelle von links und rechts abzurufen und zu ersetzen:

 function child(root::AVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function insert_child!(root::AVLNode{K,V}, newnode::Union{Nothing,AVLNode{K,V}}, side::Signed) where {K,V} newnode == nothing || (newnode.parent = root) if side == -1 root.left = newnode elseif side == 1 root.right = newnode else throw(ArgumentError("Expecting side=-1 for inserting node to the left or side=1 for inserting to the right")) end end 

Als nächstes gehen wir den Baum hinauf und suchen nach Verstößen gegen die Bedingungen 2 und 3. Als nächstes betrachten wir die Optionen, die möglicherweise angezeigt werden (in den Abbildungen zeigt Grün den Knoten an, der die Höhe geändert hat, der Knoten, der verarbeitet wird, ist sein übergeordneter Knoten).

Fall 0
Nach dem Einfügen wurde die Höhe des Knotens dieselbe wie die der Schwester und 1 kleiner als die (alte) Höhe des übergeordneten Knotens.

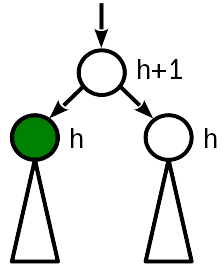
Im besten Fall müssen Sie nichts weiter berühren. Auch oben kann man da nicht mehr gucken dort wird sich nichts ändern.

Fall 1
Vor dem Einsetzen war die Höhe des Knotens gleich der Höhe des Schwesterknotens. Durch das Einfügen wird die Wurzel des Teilbaums angehoben und die Höhe des Knotens mit der Höhe des übergeordneten Knotens verglichen.

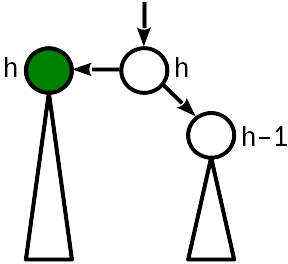
In diesem Fall reicht es aus, den übergeordneten Knoten zu „erhöhen“ und seine Höhe um 1 zu erhöhen. Gleichzeitig müssen Sie weiter zur Wurzel des Baums wechseln, da eine Änderung der Höhe des übergeordneten Knotens zu einer Verletzung von Bedingung 2 führen kann, die eine Ebene höher liegt.

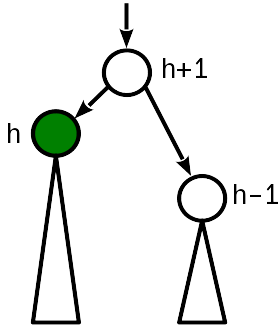
 fucntion promote!(nd::AVLNode, by::Integer=1) nd.height += by end fucntion demote!(nd::AVLNode, by::Integer=1) nd.height -= by end 

Fall 2

Nach dem Einfügen wurde der Höhenunterschied zum Schwester-Teilbaum 2, und der linke Teilbaum wurde nach oben „gedrückt“:

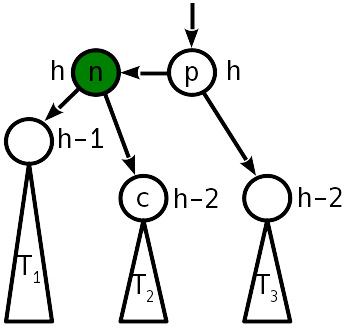
Das Problem wird mit einer Operation behandelt, die als "einfache Drehung" bezeichnet wird und den Baum wie folgt transformiert:

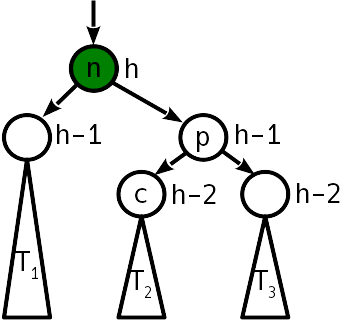
Eine einfache Drehung erfordert 6 Zeigerwechsel.

Beachten Sie, dass bei der Projektion auf die horizontale Achse die Reihenfolge der Eckpunkte n , p und der Bäume T ₁ - T ₃ vor und nach der Drehung gleich bleibt. Dies ist die Erfüllung der Bestellbedingung. Wie Sie sehen, ist nach dem Aufdrehen des Baumes kein Ausgleich mehr erforderlich.

 # pivot       function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) #  c  p insert_child!(p, c, -dir) #  p  pivot insert_child!(pivot, p, dir) pivot end 

Fall 3
Nach dem Einfügen wurde der Höhenunterschied zum Schwester-Teilbaum 2 und der rechte Teilbaum "hochgeschoben":

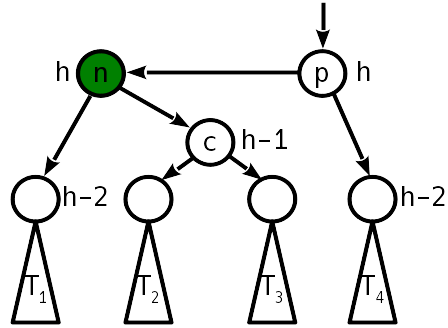
In diesem Fall hilft eine einzelne einfache Kurve nicht mehr, aber Sie können eine einfache Linkskurve um den rechten Nachkommen machen, was zu Fall 2 führt, der bereits mit einer einfachen Rechtskurve behandelt wird.

Um die Anzahl der "Übergewichtungen" von Knoten zu verringern, können zwei Windungen zu einer Operation kombiniert werden, die als große oder doppelte Windung bezeichnet wird. Anstelle von 12 Zeigeränderungen werden dann nur 10 benötigt. Als Ergebnis einer doppelten Drehung nimmt der Baum die folgende Form an:

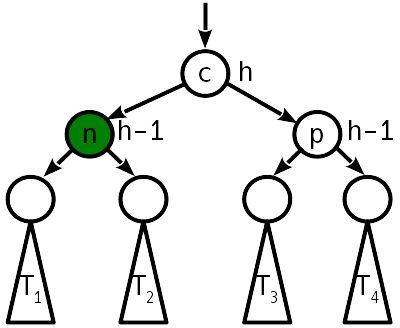
Wie Sie sehen, ist nach einer doppelten Umdrehung auch kein weiterer Ausgleich des Baumes erforderlich.

 # pivot       funtion double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) #  n  pivot  t2  n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) #  p  pivot  t3  p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end 

Wenn Sie also einen Datensatz in den AVL-Baum einfügen, benötigen Sie O (log ₂ N ) Änderungen in den Informationen über die Höhe der Knoten und nicht mehr als zwei Rotationsvorgänge. Kombinieren Sie alles zu einer Einfügefunktion. Sie unterscheidet sich von der Grundeinfügung nur dadurch, dass nach dem Einfügen eines neuen Knotens die Funktion fix_insertion!() wird, die vom neu eingefügten Knoten zur Wurzel übergeht, das Gleichgewicht überprüft und gegebenenfalls korrigiert.

 function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left #   -     if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 # true == 1, false == 0 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end 

Die Funktion fix_insertion!() Überprüft den Höhenunterschied zwischen zwei fix_insertion!() Knoten, beginnend mit dem übergeordneten Knoten und dem eingefügten. Wenn es gleich 1 ist - wir sind in Fall 1, müssen Sie die Höhe des Knotens erhöhen und höher gehen. Wenn es Null ist, ist der Baum ausgeglichen. Wenn es gleich 2 ist - dies ist Fall 2 oder 3 - müssen Sie die entsprechende Drehung anwenden, und der Baum wird in einen ausgeglichenen Zustand versetzt.

 #     -  , #   -  imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) #      0 - ..        while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 #       , # ..   dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end 

Datensatz löschen

Das Entfernen ist etwas schwieriger als das Einsetzen.

Betrachten Sie zunächst das übliche Löschen eines Eintrags aus einem binären Suchbaum.

1. Befindet sich der gelöschte Datensatz im Blatt, wird der Datensatz einfach gelöscht, hier ist alles einfach.
2. Befindet sich der gelöschte Datensatz in einem Knoten mit nur einem Nachkommen, wird dieser Nachkomme zusammen mit seinem gesamten Teilbaum an die Stelle des Remote-Knotens gesetzt.
3. Wenn zwei Nachkommen vorhanden sind, wird entweder das maximale Element im linken Teilbaum oder das minimale Element im rechten Teilbaum aus dem Baum extrahiert (durch die Eigenschaft des Suchbaums wird garantiert, dass der Knoten mit dem maximalen Element keinen rechten Nachkommen hat, und mit einem minimalen Element nach links, sodass das Löschen einfach ist) und anstelle des gelöschten Datensatzes setzen.

Danach kann das Baumgleichgewicht jedoch gestört sein. Sie müssen daher vom übergeordneten Knoten des Remote-Knotens aufsteigen und ihn wiederherstellen. Beachten Sie, dass zu Beginn garantiert ist, dass einer der Nachkommen des betreffenden Elternteils die Höhe um 1 verringert hat. Vor diesem Hintergrund müssen Sie die Optionen berücksichtigen (die Knoten, die die Höhe geändert haben, werden rot angezeigt, der verarbeitete Knoten ist der Elternteil von rot):

Fall 1
Kein Ungleichgewicht. Vor dem Entfernen war es also 1 Modulo, und jetzt sind die untergeordneten Knoten 2 niedriger als die übergeordneten.

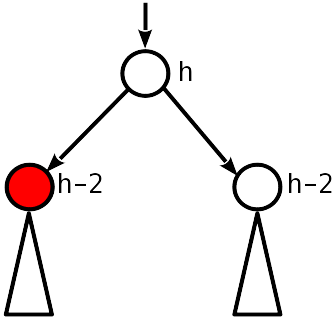
Sie müssen den übergeordneten Knoten um 1 senken und weiter nach oben gehen.

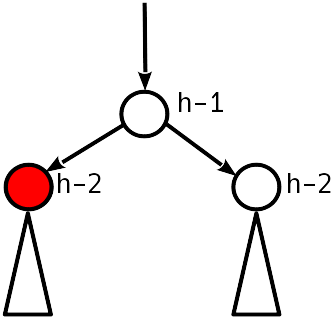
Fall 2
Ungleichgewicht 1 Modulo.

Wenn die AVL-Bedingung erfüllt ist, können Sie aufhören.

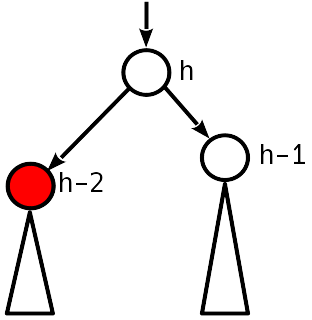
Fall 3
Das Ungleichgewicht 2 ist modulo, der Schwesterknoten zum absteigenden Knoten hat ein Ungleichgewicht ungleich Null.

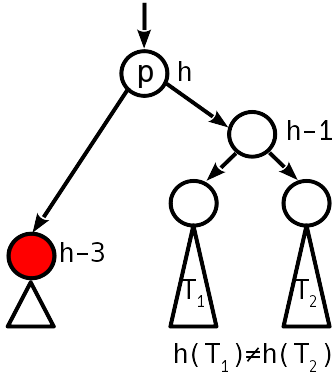
Wir stellen das Gleichgewicht durch einfaches (wenn T ₁ niedriger als T _{2 ist} ) oder durch doppelte (ansonsten) Drehung wieder her, wie dies beim Einsetzen geschehen ist. Die Höhe des Teilbaums nimmt ab, d.h. Über dem Baum kann eine Verletzung auftreten.

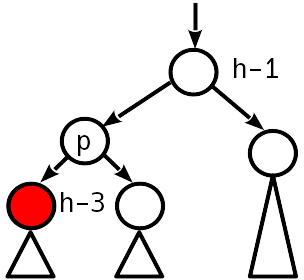
Fall 4
Ungleichgewicht 2 Modulo, der Schwesterknoten hat kein Ungleichgewicht.

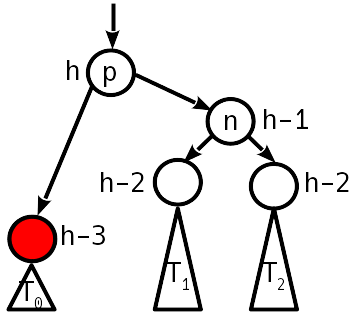
Eine einfache Drehung stellt den Ausgleichszustand wieder her, während sich die Höhe des Teilbaums nicht ändert - wir hören auf, uns nach oben zu bewegen.

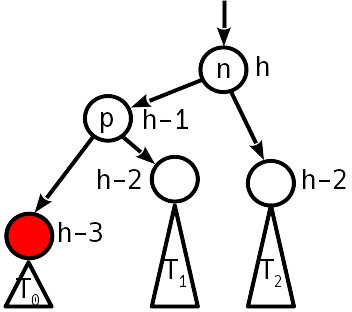
 function next_node(node::AVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::AVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::AVLNode) node = start skew = imbalance(node) while (node !== node.parent) && (abs(skew) != 1) if skew != 0 @assert abs(skew) == 2 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) < 2 if prev_skew == dir node = double_rotate!(child(n, dir), dir) else node = rotate!(n, dir) prev_skew != 0 || break end else node.height -= 1 end node = node.parent skew = imbalance(node) end end 

Aufstieg und Fall von AVL-Bäumen

Ein nicht sehr schönes Merkmal klassischer AVL-Bäume ist die Schwierigkeit, einen Datensatz zu löschen: Eine Rotation kann den gesamten Teilbaum um eine Ebene nach unten "zurücksetzen". Im schlimmsten Fall erfordert das Löschen O (log ₂ N ) fix_deletion!() - jedes Mal, wenn Sie in fix_deletion!() um eine Ebene nach fix_deletion!() .

Aufgrund dieses nicht so guten asymptotischen Verhaltens wichen AVL-Bäume rot-schwarzen Bäumen, die in den 1970er Jahren auftauchten und einen schwächeren Ausgleichszustand aufwiesen - der Weg von der Wurzel zum am weitesten entfernten Blatt ist nicht mehr als doppelt so lang wie der Weg von der Wurzel zum nächsten Blatt. Aus diesem Grund beträgt die Höhe von rot-schwarzen Bäumen im schlimmsten Fall ₂ log ₂ N gegenüber 1,44 log ₂ N für AVL-Bäume. Das Löschen eines Datensatzes erfordert jedoch nicht mehr als drei einfache Umdrehungen. Daher verlieren Suche und Einfügung aufgrund einer höheren Baumhöhe möglicherweise an Leistung, aber es gibt einen potenziellen Gewinn, wenn Einfügungen häufig mit Löschungen durchsetzt sind.

AVL schlägt zurück

Es stellt sich heraus, dass der „ideale“ Algorithmus zum Erstellen von binären Suchbäumen eine geringe Höhe (auf der Ebene des klassischen AVL-Baums) und eine konstante Anzahl von Umdrehungen sowohl beim Hinzufügen als auch beim Löschen eines Datensatzes gewährleisten sollte. Dies wurde noch nicht erfunden, aber 2015 wurde eine Arbeit veröffentlicht, die eine Struktur vorschlug, die die Eigenschaften von AVL- und rot-schwarzen Bäumen verbessert. Die Idee liegt näher an den AVL-Bäumen, aber die Balance-Bedingung wird gelockert, um ein effizienteres Löschen von Datensätzen zu ermöglichen. Die Eigenschaften einer Struktur, die als "schwacher AVL-Baum" (W (eak) AVL-Baum) bezeichnet wird, werden wie folgt formuliert:

1. Reihenfolge: Für jeden Knoten ist der Schlüssel oben im linken Teilbaum kleiner als der Schlüssel oben im rechten Teilbaum (wenn die Nachkommen keine leeren Knoten sind).
2. Aufsteigender Rang. Jedem Knoten wird ein Rang zugewiesen. Der Rang aller leeren Knoten ist Null, der Rang der Blätter ist 1. Der Rang des Elternknotens ist streng höher als der Rang des Kindes.
3. Schwaches ABL-Gleichgewicht: Der Rang eines Knotens unterscheidet sich vom Rang der untergeordneten Knoten um nicht mehr als 2.

Es stellt sich heraus, dass eine solche Struktur die Eigenschaften sowohl klassischer AVL-Bäume als auch rot-schwarzer Bäume umfasst. Insbesondere wenn wir die Bedingung einführen, dass sich beide untergeordneten Knoten im Rang nicht um 2 vom übergeordneten Knoten unterscheiden können, erhalten wir einen regulären AVL-Baum, und der Rang entspricht genau der Höhe des Teilbaums.

Das Schöne an SAVL-Bäumen ist, dass durch eine leichte Abschwächung des AVL-Zustands der Baum ausgeglichen werden kann, wenn ein Datensatz um nicht mehr als zwei Umdrehungen gelöscht wird! Die Baumhöhenschätzung ist h <min (1,44 log ₂ M , ₂ log ₂ N ), wobei N die Anzahl der Einträge im Baum ist, M die Anzahl der Einfügungen ist, verglichen mit h < ₂ log ₂ N für rot-schwarze Bäume. , - , , .

- , . - .

.

-, "" "". , :

 mutable struct WAVLNode rank::UInt8 key::K value::V left::Union{Nothing, WAVLNode{K,V}} right::Union{Nothing, WAVLNode{K,V}} parent::WAVLNode{K,V} #   function WAVLNode{K,V}() where {K,V} node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing return node end #    - function WAVLNode{K,V}(key, value) where {K,V} key, value = convert(K, key), convert(V, value) node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end struct WAVLTree{K, V} entry::WAVLNode{K,V} WAVLTree{K,V}() where {K,V} = new{K,V}(WAVLNode{K,V}()) end function child(root::WAVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function Base.getindex(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) node = avlt.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end 

, -. : 1 , — , 0 ( ) 1 ( ). imbalance() , , .

 wavlrank(node::Union{Nothing,WAVLNode}) = node == nothing ? 0 : Int(node.rank) function imbalance(node::WAVLNode) rr, lr = wavlrank(node.right), wavlrank(node.left) skew = rr - lr diff = node.rank - max(rr, lr) skew, diff end 

, . , , , , -, - .

 # pivot       function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) #  c  p insert_child!(p, c, -dir) #  p  pivot insert_child!(pivot, p, dir) pivot end # pivot       function double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) #  n  pivot  t2  n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) #  p  pivot  t3  p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left #   -     if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end 

, — -. .

0
, ..:

1. 1, 1
2. 0, 2 , .
   .

1
2 ( 0, 2 ).
1 .

2
1, 2.

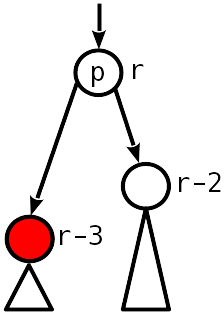
1, .

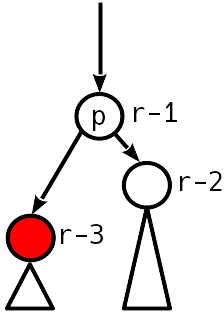
3
2 ( 1, .. ), 2 .

, . .

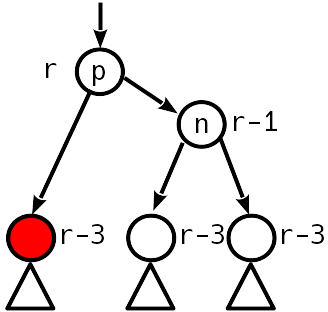
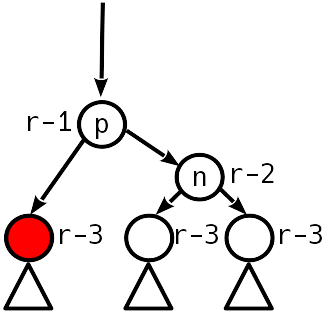
4

.

, , , .. .

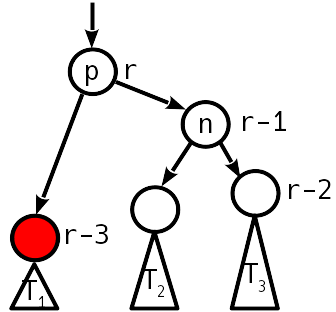
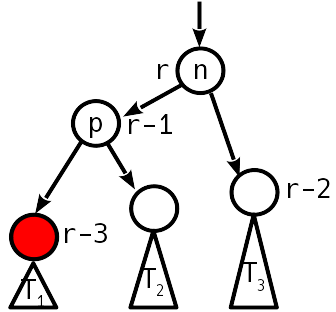
— T ₁ T ₂ , p 2, p 1.

5

.

, , .

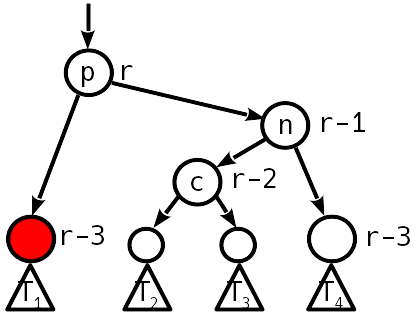
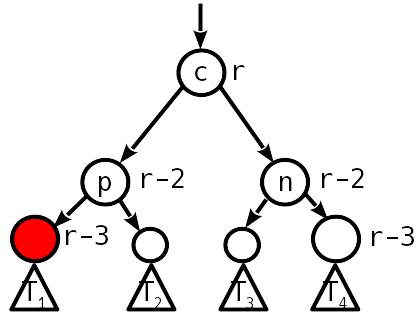
 function next_node(node::WAVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::WAVLNode) node = start skew, diff = imbalance(node) while (node !== node.parent) if skew == 0 if node.right == nothing node.rank = 1 else break end elseif abs(skew) == 1 if diff == 1 break else node.rank -= 1 end else dir = -skew ÷ 2 n = child(node, -dir) prev_skew, prev_diff = imbalance(n) if prev_diff == 2 @assert prev_skew == 0 n.rank -= 1 node.rank -= 1 elseif prev_skew == dir double_rotate!(child(n, dir), dir) break else rotate!(n, dir) break end end node = node.parent skew, diff = imbalance(node) end end 

-.

 julia> const wavl = WAVLTree{Int, Int}() julia> const avl = AVLTree{Int, Int}() julia> const dd = Dict{Int,Int}() julia> x = trues(1_000_000) #       ~  julia> for i = 1:1_000_000; dd[i] = avl[i] = wavl[i] = i * i; end julia> for i=1:500_000 k = rand(1:1_000_000) x[k] = false delete!(avl, k) delete!(wavl, k) delete!(dd, k) end # ,     julia> const y = Int[] julia> for i in eachindex(x); if x[i] push!(y, i); end; end julia> @btime let s = 0.0; for idx in y; s += dd[idx]; end; s; end 57.626 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += wavl[idx]; end; s; end 57.796 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += avl[idx]; end; s; end 53.884 ms (0 allocations: 0 bytes) 2.0238199367708794e17 

, , . , , - , -, .

— ?
— , . , , .

.

— , . n - . , , .. , .

*

— , " ", " ", " -", " ". , , -. . , .

*
** O (1), ...

, " — ". , . — ( ) , , , . .

*
** ,

() — , , , , , . — , .. , , .

Referenzen

1. "-" nickme
2. Rank-Balanced Trees by Bernhard Haeupler, Siddhartha Sen, Robert E. Tarjan // ACM Transactions on Algorithms | June 2015, Vol 11(4) pdf
3. Goodrich MT, Tamassia R. Algorithm Design and Applications