Hallo allerseits! Kürzlich entdeckte die Sprache Rust. Er teilte seine ersten Eindrücke in einem früheren Artikel . Jetzt habe ich beschlossen, etwas tiefer zu graben, dafür brauchst du etwas Ernsthafteres als die Liste. Meine Wahl fiel auf den Merkle-Baum. In diesem Artikel möchte ich:
- Sprechen Sie über diese Datenstruktur
- Schau dir an, was Rust schon hat
- Bieten Sie Ihre Implementierung an
- Leistung vergleichen
Merkle Tree
Dies ist eine relativ einfache Datenstruktur, über die es im Internet bereits viele Informationen gibt, aber ich denke, mein Artikel wird ohne eine Beschreibung des Baums unvollständig sein.
Was ist das Problem
Der Merkle-Baum wurde 1979 erfunden, gewann aber dank der Blockchain an Popularität. Die Blockkette im Netzwerk ist sehr groß (für Bitcoin sind es mehr als 200 GB), und nicht alle Knoten können sie abpumpen. Zum Beispiel Telefone oder Registrierkassen. Sie müssen jedoch wissen, ob diese oder jene Transaktion in den Block aufgenommen wird. Hierzu wurde das Protokoll SPV - Simplified Payment Verification erfunden.
Wie ein Baum funktioniert
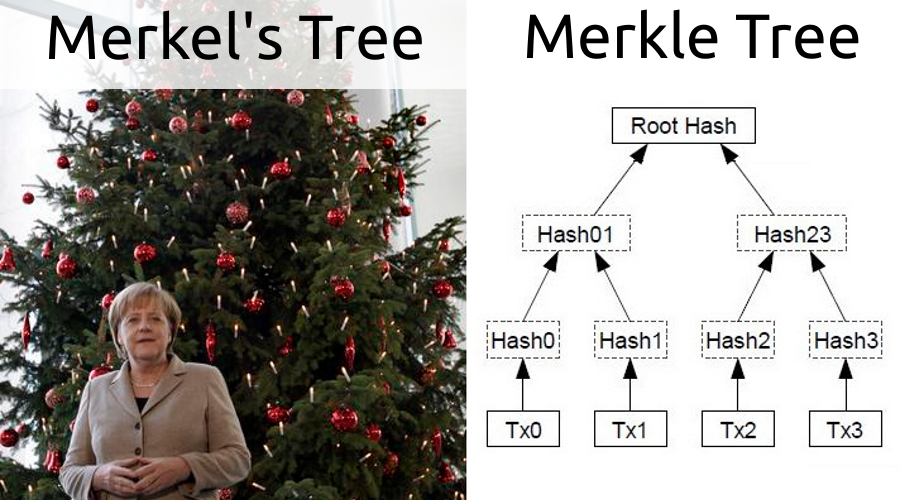
Dies ist ein binärer Baum, dessen Blätter Hashes von Objekten sind. Um die nächste Ebene zu erstellen, werden Hashes benachbarter Blätter paarweise verkettet und der Hash aus dem Ergebnis der Verkettung berechnet, was im Bild in der Kopfzeile dargestellt ist. Somit ist die Wurzel des Baumes ein Hasch aller Blätter. Wenn Sie ein Element entfernen oder hinzufügen, ändert sich der Stamm.
Wie funktioniert ein Baum?
Mit einem Merkle-Baum können Sie Beweise für die Aufnahme einer Transaktion in einen Block als Pfad von einem Transaktions-Hash zum Stamm erstellen. Zum Beispiel sind wir an der Transaktion Tx2 interessiert, dafür wird der Beweis sein (Hash3, Hash01). Dieser Mechanismus wird auch in SPV verwendet. Der Client lädt nur den Blockheader mit seinem Hash herunter. Bei einer Transaktion von Interesse fordert er einen Beweis von einem Knoten an, der die gesamte Kette enthält. Dann macht es eine Überprüfung, für Tx2 wird es sein:
hash(Hash01, hash(Hash2, Hash3)) = Root Hash
Das Ergebnis wird mit der Wurzel des Blockheaders verglichen. Dieser Ansatz macht es unmöglich, Beweise zu fälschen, da in diesem Fall das Testergebnis nicht mit dem Inhalt des Headers konvergiert.
Welche Implementierungen existieren bereits?
Rust ist eine junge Sprache, aber viele Erkenntnisse des Merkle-Baumes sind bereits darauf geschrieben. Nach Github zu urteilen, ist dies im Moment 56 mehr als in C und C ++ zusammen. Obwohl Go sie mit 80 Implementierungen auf den neuesten Stand bringt.
Für meinen Vergleich habe ich diese Implementierung anhand der Anzahl der Sterne im Repository ausgewählt.
Dieser Baum ist auf die offensichtlichste Weise konstruiert, dh es handelt sich um ein Diagramm von Objekten. Wie bereits erwähnt, ist dieser Ansatz nicht vollständig rostfreundlich. Beispielsweise ist es nicht möglich, eine bidirektionale Kommunikation von Kindern zu Eltern herzustellen.
Die Konstruktion von Beweisen erfolgt durch eine eingehende Suche. Wenn ein Blatt mit dem richtigen Hash gefunden wird, ist der Pfad dazu das Ergebnis.
Was kann verbessert werden
Es war für mich nicht interessant, eine einfache (n + 1) -te Implementierung durchzuführen, also dachte ich über Optimierung nach. Der Code für meinen Vektor-Merkle-Baum ist auf Github .
Datenspeicherung
Das erste, was mir in den Sinn kommt, ist, den Baum in ein Array zu verschieben. Diese Lösung ist in Bezug auf die Datenlokalität viel besser: mehr Cache-Treffer und eine bessere Vorladung. Das Gehen um Objekte, die aus dem Gedächtnis verstreut sind, dauert länger. Eine bequeme Tatsache ist, dass alle Hashes gleich lang sind, weil berechnet von einem Algorithmus. Der Merkle-Baum im Array sieht folgendermaßen aus:

Beweis
Wenn Sie den Baum initialisieren, können Sie eine HashMap mit allen Blattindizes erstellen. Wenn es also kein Blatt gibt, müssen Sie nicht um den ganzen Baum herumgehen, und wenn ja, können Sie sofort dorthin gehen und sich zur Wurzel erheben, um einen Beweis zu erstellen. In meiner Implementierung habe ich HashMap optional gemacht.
Verkettung und Hashing
Es scheint, dass hier verbessert werden kann? Immerhin ist alles klar - nehmen Sie zwei Hashes, kleben Sie sie und berechnen Sie einen neuen Hash. Tatsache ist jedoch, dass diese Funktion nicht kommutativ ist, d.h. Hash (H0, H1) ≠ Hash (H1, H0). Aus diesem Grund müssen Sie sich beim Erstellen des Proofs merken, auf welcher Seite sich der benachbarte Knoten befindet. Dies erschwert die Implementierung des Algorithmus und macht das Speichern redundanter Daten erforderlich. Alles ist sehr einfach zu reparieren, sortieren Sie einfach die beiden Knoten vor dem Hashing. Zum Beispiel habe ich Tx2 unter Berücksichtigung der Kommutativität zitiert. Die Prüfung sieht folgendermaßen aus:
hash(hash(Hash2, Hash3), Hash01) = Root Hash
Wenn Sie sich keine Gedanken über die Reihenfolge machen müssen, sieht der Überprüfungsalgorithmus wie eine einfache Faltung eines Arrays aus:
pub fn validate(&self, proof: &Vec<&[u8]>) -> bool { proof[2..].iter() .fold( get_pair_hash(proof[0], proof[1], self.algo), |a, b| get_pair_hash(a.as_ref(), b, self.algo) ).as_ref() == self.get_root() }
Das Nullelement ist der Hash des gewünschten Objekts, das erste ist sein Nachbar.
Lass uns gehen!
Die Geschichte wäre unvollständig ohne einen Leistungsvergleich, der mehrmals länger dauerte als die Implementierung des Baums. Für diese Zwecke habe ich das Kriterien- Framework verwendet. Die Quellen der Tests selbst sind hier . Alle Tests finden über die TreeWrapper- Schnittstelle statt, die für beide Probanden implementiert wurde:
pub trait TreeWrapper<V> { fn create(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); fn find(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); fn validate(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); }
Beide Bäume arbeiten mit derselben Ringkryptographie. Hier werde ich nicht verschiedene Bibliotheken vergleichen. Ich habe am häufigsten genommen.
Als Hash-Objekte werden zufällig generierte Zeichenfolgen verwendet. Bäume werden auf Arrays unterschiedlicher Länge verglichen: (500, 1000, 1500, 2000, 2500 3000). 2500 - 3000 ist die ungefähre Anzahl der Transaktionen im Bitcoin-Block.
In allen Diagrammen gibt die X-Achse die Anzahl der Array-Elemente (oder die Anzahl der Transaktionen im Block) an, und die Y-Achse gibt die durchschnittliche Zeit an, um den Vorgang in Mikrosekunden abzuschließen. Das heißt, je mehr desto schlimmer.
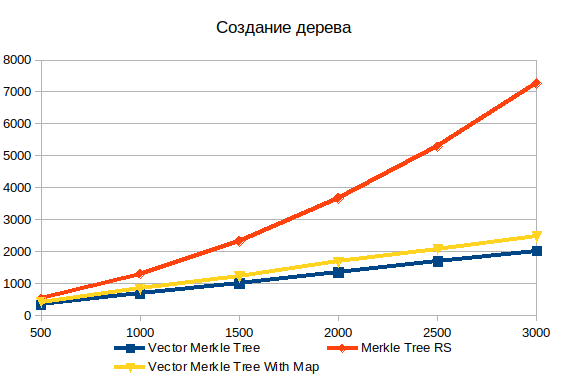
Baum machen
Die Speicherung aller Baumdaten in einem Array übersteigt das Leistungsdiagramm von Objekten erheblich. Für ein Array mit 500 Elementen das 1,5-fache und für 3000 Elemente bereits das 3,6-fache. Die nichtlineare Natur der Abhängigkeit der Komplexität vom Volumen der Eingabedaten in der Standardimplementierung ist deutlich sichtbar.
Außerdem habe ich im Vergleich zwei Varianten des Vektorbaums hinzugefügt: mit und ohne HashMap . Durch das Ausfüllen einer zusätzlichen Datenstruktur werden etwa 20% hinzugefügt, aber Sie können beim Erstellen von Beweisen viel schneller nach Objekten suchen.
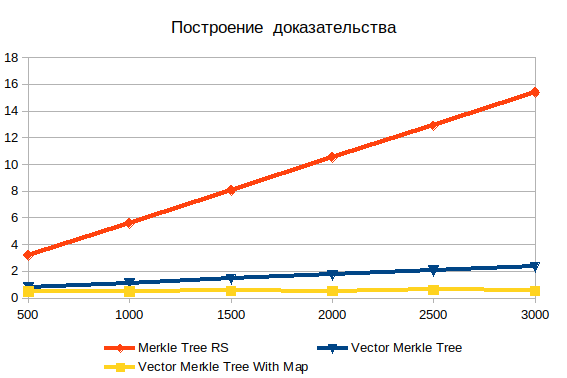
Beweise bauen
Hier sehen Sie die offensichtliche Ineffizienz der Suche in der Tiefe. Mit zunehmendem Input wird es nur noch schlimmer. Es ist wichtig zu verstehen, dass die gewünschten Objekte Blätter sind, daher kann es kein Komplexitätsprotokoll (n) geben . Wenn die Daten zuvor gehasht wurden, ist die Betriebszeit praktisch unabhängig von der Anzahl der Elemente. Ohne Hashing wächst die Komplexität linear und besteht in der Brute-Force-Suche.
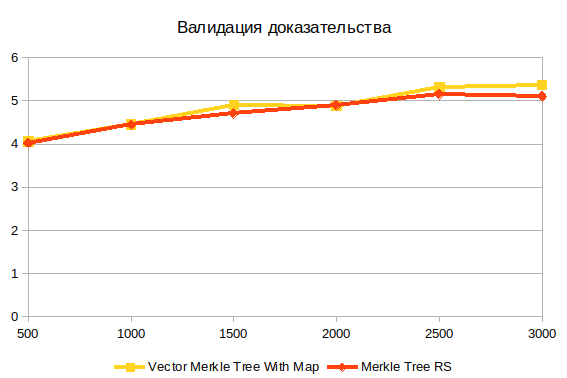
Validierung von Beweisen
Dies ist die letzte Operation. Es kommt nicht auf die Struktur des Baumes an, weil arbeitet mit dem Ergebnis der Beweiserstellung. Ich glaube, dass die Hauptschwierigkeit hier die Hash-Berechnung ist.
Zusammenfassung
- Die Art und Weise, wie Daten gespeichert werden, wirkt sich stark auf die Leistung aus. Wenn alles in einem Array viel schneller ist. Und die Serialisierung einer solchen Struktur wird sehr einfach sein. Die Gesamtmenge an Code wird ebenfalls reduziert.
- Das Verketten von Knoten mit dem Sortieren vereinfacht den Code erheblich, macht ihn jedoch nicht schneller.
Ein bisschen über Rust
- Gefiel der Kriterienrahmen . Es liefert klare Ergebnisse mit Durchschnittswerten und Abweichungen, die mit Grafiken ausgestattet sind. Kann verschiedene Implementierungen desselben Codes vergleichen.
- Mangelnde Vererbung beeinträchtigt das Leben nicht wesentlich.
- Makros sind ein mächtiger Mechanismus. Ich habe sie in meinen Baumtests zur Parametrisierung verwendet. Ich denke, wenn sie schlecht verwendet werden, können Sie so etwas tun, dass Sie selbst später nicht glücklich sind.
- An einigen Stellen langweilte sich der Compiler mit seinen Speicherprüfungen. Meine anfängliche Annahme, dass der Beginn des Schreibens in Rust so einfach nicht funktioniert hat, war richtig.
Referenzen