Über die Verwendung parametrischer Methoden zur Spektralschätzung im Radar - die MUSIC-Methode. Ergänzung zum Artikel

Ich bin auf einen guten Artikel über die Methode der Spektralschätzung gestoßen, der sich hervorragend für ein kurzes Signal aus der Summe der rauscharmen Harmonischen eignet. (-copy) Vielleicht helfen meine Kommentare dem Leser, die Essenz der Methode zu verstehen. Was mich ein wenig verärgerte, waren die unvollständig implementierten Fähigkeiten der Methode. Die Methode wird für Radar verwendet - um schnell die Richtung der eingehenden Signale (Winkel θ) mit dem nachfolgenden Ziel der automatischen, es versteht sich, Anpassung des Systems zu bestimmen. Aber - der Autor erstellt keine numerische Definition dieses Winkels (und dies ist im Kontext seltsam), obwohl diese Definition durchaus möglich ist. Wir haben nur schöne Grafiken, nach denen das System, wie sich herausstellt, immer noch "crawlen" und "crawlen" muss, um die Anzahl und Position der Maxima zu bestimmen, was nicht ganz gut ist.


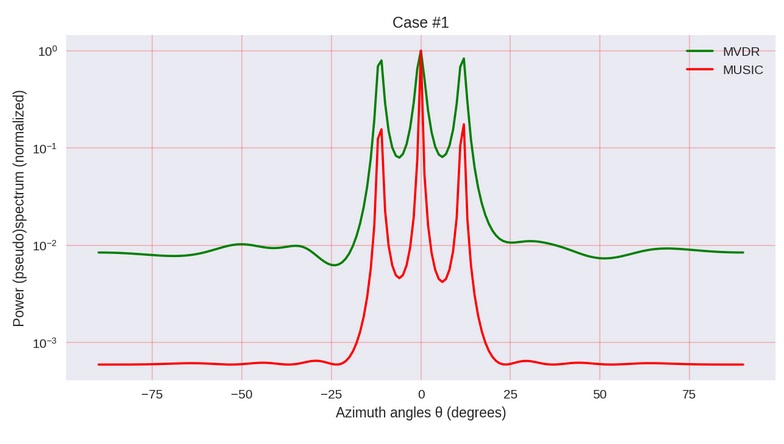Illustration des Autors des genannten Artikels

"Erklärung des Problems"

Kurz gesagt: Wir müssen irgendwie bestimmen, wo (in welchem ​​Winkel) das Signal von der Gitterantenne kommt. Dann in die Richtung einstellen - aber das ist nicht mehr in diesem "Lied".

"Modellierung des empfangenen Signals"



(Es ist nicht wichtig - anscheinend sollte das "Symbol" überall als "Signal" gelesen werden.)

Hier sei vorsichtig. Der Autor scheint mit einem bestimmten komplexen Signal (räumlich) zu arbeiten. Obwohl X , ja, wie geschrieben, eine Matrix von "komplexen Amplituden" sein könnte (abhängig nicht von der Koordinate, sondern von der Raumfrequenz), sind XX ^H beispielsweise "Kovarianzen" und keine "Spektraldichten".

S ähnelt eher der Matrix der „komplexen Amplituden“, mit deren Hilfe harmonische Komponenten (Nutzsignal) modelliert werden. Weder additive Geräusche noch harmonische Komponenten scheinen hier ein analytisches Signal zu sein. Obwohl Oberschwingungen mit Vorbehalten sehr nahe daran liegen.



"# Allgemeine Formel:
# sqrt (N0 / 2) * (G1 + jG2),
# wobei G1 und G2 unabhängige Gaußsche Prozesse sind. ”

Die Hauptsache ist, woher die imaginäre Komponente aus realen Messungen stammt, irgendwie ist es nicht klar. Das analytische Signal kann grundsätzlich berechnet werden.

Es ist möglich, dass es eine „Quelle“ gibt, an der sie mit echtem X (empfangenes Signal) gearbeitet haben. Zum Beispiel scheint der Autor sehr daran interessiert gewesen zu sein, die resultierenden Spektren symmetrisch (gerade) zu machen - in allen betrachteten Fällen werden die Testsignale durch die symmetrisch links und rechts eintreffenden Signale gegeben.

"Bedingungen"

Wir haben den Winkelbereich θ der Ankunft des Signals bestimmt, in dem es sinnvoll ist, zu schauen. Richtig, dann bauen wir die Grafiken trotzdem aus irgendeinem Grund von +90 bis -90 Grad.

"Eine kleine Theorie über die Methode selbst"

Ergänzung. MUSIK wird aus der autoregressiven Schätzung (aus den Yule-Walker-Gleichungen) fast von selbst erhalten, wenn die Varianz des bedingten weißen Rauschens vernachlässigbar ist. Die Ergebnisse sind fast gleich. Die SLAE-Lösung ist noch etwas wirtschaftlicher als die Suche nach Eigenvektoren, aber aus einer Reihe von Gründen wäre die spektrale Zerlegung der Kovarianzmatrix mit ihrer schlechten Konditionalität in jeder Hinsicht sehr wünschenswert.

EVD ist in der Tat einfach = "Finden von Eigenwerten und Vektoren" und nichts weiter. Kein Algorithmus.

Warum schreiben wir ein "Pseudospektrum" - weil das Spektrum nur aus den Eigenvektoren der Kovarianz- (Korrelations-) Matrix nur bis zu einem Skalierungsfaktor bestimmt werden kann, d.h. Die resultierenden absoluten Werte sind nicht sinnvoll. Aber wir brauchen genau und nur die Position der Maxima.



- Das ist das interessanteste. Zunächst einmal sind U ₀ bereits Eigenvektoren, nur für die Kovarianzmatrix - und das "Speichern" bei ihrer Suche schlägt fehl. Weiter. Die Suche nach Lösungen führt dazu, dass die Wurzeln der Leistungsgleichung bestimmt werden müssen, was einer anderen spektralen Zerlegung absolut äquivalent ist. Der Autor verwechselt offenbar die Eigenwerte völlig unterschiedlicher Matrizen.

Aber ... die Hauptsache ... jetzt (!), Endlich (!), Wir könnten die Wurzeln logarithmieren und die komplexen „Impedanzen“ (Modellpole) numerisch bestimmen (in der Gleichung ist dies wieder θ, was nicht sehr gut ist), was Ihr Imaginärteil zeigt genau diesen Winkel, in dem das Signal kam. Es ist sehr bedauerlich, dass der Autor dies nicht getan hat.

"Modellierung"



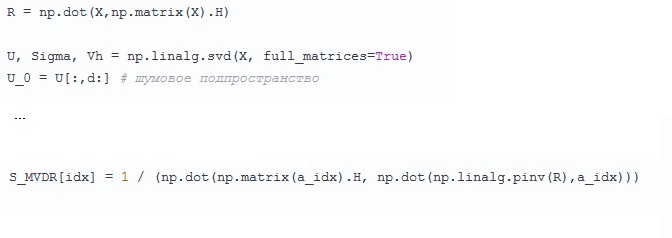
Hier ist ein wenig alarmierend - zuerst wurde die Kovarianzmatrix R = XX ^H berechnet, die aus irgendeinem Grund für einige Zeit vergessen wurde und von vorne anfing - zerlegt in singuläre Zahlen und Vektoren X. Sie versprachen per Text, nach den Eigenwerten und dem Vektor R zu suchen, was natürlich der gleiche ist, aber sozusagen logischer, wenn R bereits gefunden wurde. Es ist nicht klar, auf welches Problem der Autor gestoßen ist.

Wir erinnern uns an R, wenn wir das Spektrum unter Verwendung der Minimendispersionsmethode MVDR bewerten. Und hier ist es auch interessant - R , nach dem Drehbuch zu urteilen, scheint in voller Übereinstimmung mit dieser Methode auf klassische Weise ohne SVD (Pseudo-Inversion) umgekehrt worden zu sein, obwohl es niedrigrangig (stark entartet) zu sein scheint. Ich meine, sind unsere Geräusche so klein? Na vielleicht.

Wirklich verwirrt hier das. Die Größe des "Rauschunterraums" im Skript scheint durch die Willensreihenfolge (gleich d) zugewiesen zu sein. Im wirklichen Fall wissen wir jedoch nicht, wie viele Harmonische das Signal enthält und wie viele Geräusche. Es war notwendig, diese Eigenwerte zu analysieren - welche von ihnen sind vernachlässigbar, welche nicht.

Im Allgemeinen ist die Arbeit sehr interessant, nicht nur für Radar. Ich glaube, die Methode hat ein großes Potenzial, nur für diese Art von Signalen. Der Autor hat sehr gut gearbeitet, und einige nervige Inkonsistenzen sind nicht so schwer zu beheben. Die Hauptsache ist, den Artikel mit der RootMUSIC-Methode zu ergänzen.